|
| |
| |
| |
Notes marginales aux Acta Eruditorum
| |
| |
Notes marginales aux Acta Eruditorum
d'après les lettres du 9 juin, du 21 juillet et du 12 septembre 1696 de Jean Bernoulli à Leibniz.
Vu la promesse faite au T. IX (voyez la note 112 de la p. 764 qui précède) nous jugeons de notre devoir de publier ces notes marginales, quoique plusieurs d'entre elles ne soient pas de grande importance, en indiquant les passages auxquels elles se rapportent, sans toutefois y ajouter des figures. Pour bien comprendre la portée des notes le lecteur devra en général consulter les Acta Eruditorum eux-mêmes. Nous avons toutefois reproduit quelques figures se rapportant à un article de Tschirnhaus de 1690 puisqu'en cet endroit il ne s'agit pas d'une note marginale proprement dite mais d'un petit article de Huygens écrit sur une feuille séparée.
Nous imprimons en italiques les lignes auxquelles, suivant Bernoulli, se rapportent les remarques de Huygens.
| |
Année 1682.
Notes appartenant à l'article de Leibniz ‘De vera proportione circuli ad quadratum circumscriptum in numeris rationalibus.’
| texte de l'auteur. |
remarques de huygens. |
| |
| pag. 45. l. 20 et 21. Et quoniam quotcunque terminorum numero finitorum progressionis harmonicoe summa, compendio aliquo iniri potest...Ga naar voetnoot1) |
Non novi hoc compendium. |
| |
| pag. 46. l. ultimâ. Hyperbolae vero...portio CBEHC quae logarithmum rationis ipsius AE ad AB (sive binarit) reproesentat, erit ⅜ + 1/48 + 1/120 etc. |
Imo ¼ + 1/32 + 1/256 etc. secundum Wallisium. |
Note appartenant à l'article sur celui de Tschirnhaus ‘Inventa nova exhibita Parisiis Societati Regiae Scientiarum’.
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| pag. 365. l. 7, 8, 9. Et sic proetendit Autor quod punctum hoc H sit aliquod ex infinitis, quoe constituunt curvam BHE à radiis reflexis formatam... |
Fallitur Author. |
| |
Année 1683.
Note à l'article de Tschirnhaus ‘Methodus auserendi omnes terminos intermedios ex data aequatione’.
| pag. 207. l. 23...Radicem desideratam oequationis y3-py-1=0. |
Hoc jam diu notum etiam Vietae puto. |
Notes à l'article de Tschirnhaus ‘Methodus datae figurae, rectis lineis et curva geometrica terminatae, aut quadraturam, aut impossibilitatem ejusdem quadraturae determinandi.
| pag. 433. l. 26, 27. Si vero sit curva aliqua mechanica, spatium ACB tam quoad totum, quam omnes suas partes, erit mechanice quadrabile, seu quadratura hujus geometrice non poterit inveniri. |
Valde dubito de consequentia. |
| |
| pag. 435. l. 14. Quoe omnia si restituantur, obtinetur zz=9aax-12axx+4x3/2a-x curvae AFB explicans naturam... |
Nihil explicat. |
| |
| ibid. l. 17, 18, 19. Eadem ratione alia ac alia assumpta curva geometrica AHD, alia ac alia curva geometrica AFB invenitur, et quadrabilis; unde sic quidem patet, qua ratione hoec theoremata omnes quadr atur as possibiles includant. |
Hoc idem jam diu praestitit Barovius in suis Lectionibus. |
| |
| pag. 437. l. 2. Ex his vero abunde constabit, qua ratione ope similium Theorematum...aut quadratura possit exhiberi, aut ejusdem impossibilitas demonssrari... |
Sed nihil potest intelligi hactenus quidem. |
| |
Année 1684.
Notes à l'article de Halley ‘Epistola theoriam motus satellitis Saturnii corrigens’, d'après sa pièce dans les Philos. Trans. de 1683.
| p. 188. fig. 2. |
Fig. 2 sic corrigenda...minuta horarum erant transposita. mihi verus positus sic notatus est... |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| pag. 189. l. penult. Hinc motus diurnus 22o 34′ 38″ 18‴. |
Cassinus quoque habet 22o 34′ 38″. Sed quare in tabulâ seq. ponit Hallejus 22o 35′ miror. quia non habet ter. sec. |
| |
| pag. 191. l. 5. 0.22o 35′ |
0.22o 34′ 38″ Cassino, 0.22o 34′ 44″ mihi. |
Notes à l'article de Leibniz ‘De dimensionibus figurarum inveniendis’.
| pag. 233. l. ultimâ...data curva AFC, potest inveniri curva AGD talis naturoe, ut rectangulum sub FE ordinata prioris curvae, et recta constante H, semper aequetur trilineo curvae posterioris seu figurae AEGA; |
Hoc ex lectionibus Barrovi. |
| |
| pag. 234. l. 2, 3. vel ut rectangulum sub FE ordinata curvoe priorie, et abscissa ejus AF, oequetur eidem trilineo; vel aliis modis infinitis. |
Hoc non vidi, qui... |
| |
| ibid. l. 12, 13. Adhibeo aequationes curvarum generales, quarum unaquaeque omnes curvas ejusdem gradus exprimit. Et talis curvoe generalis, consideratoe tanquam quadratricis, quoero quadrandam generalem, secundum aliquem ex modis supra dictis, quem semper eundem servo. |
Ergo facienda tabula quandrandarum seu quadrabiliumabsque signis + et -, nam alias insinitus esset labor: factâ autem comparatione videndum, quo modo in congruâ istâ formulâ etiam signa possint evadere eadem quae in aequatione propositâ. |
| |
| pag. 235. l. 3, 4. Hujusmodi coggitationum mearum, quas alibi non observavi, participem feci amicum ingeniosissimum... |
Dn. Tschirnhaus. |
| |
| ibid. l. 6...calculum inveniendi quadratrices algebraicas supra dicto methodo aggressus aliquot theoremata dedit. |
Ao 1683. |
| |
| pag. 236. l. 5. deberet haec aequatio secundum alibi proposita conferri posse cum ista... |
ubinam? |
Notes à l'article de Leibniz ‘Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas, nec irrationales quantitates moratur, et singulare pro illis calculi genus’.
| pag. 469. l. 7, 8, 9, 10, 11, 12...Y-1... |
Y-1 est 1/Y |
| |
pag. 472. l. 10. jam dl est - 2dx - 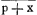 |
+ 2dx - 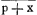 |
| |
| |
| |
Année 1685.
Note à un article sur le livre de Valentin Estancel S.J. ‘Uranophilus coelestis peregrinus five mentis uranicae per mundum sidereum peregrinantis Extases’. Gandavi anno 1685 in 4.
| texte de l'auteur. |
ramarques de huygens. |
| |
| pag. 235. l. 17, 18. Triginta circiter anni sunt, ex quo Athanasius Kircher, sub Itineris Extatici schemate, coelestis expansi, siderumque errantium et inerrantium naturam, vires, proprietates, compositionem et structuram publico scripto exposuit. Tanto tum passim applausu eruditiorum exceptus est liber... |
Propter titulum credo. |
Note à la ‘Nova methodus Cassiniana observandi parallaxes et distantias planetarum a terra, tentata Romae a Clar. Abbate Fr. Blanchino’, etc. in literis a. 1685 d. 15 Sept. Roma datis.
| pag. 478. l. 25. Si assumas parallaxim [Martis] rotunde 40″ erit distantia ejus a terra semidiam. plusquam 5100. |
debebat esse multo major. |
| |
Année 1686.
Note à l'article de Leibniz ‘Brevis demonstratio erroris memorabilis Cartesii et aliorum circa legem naturae, secundum quam volunt a Deo eandem semper quantitatem motus conservari; qua et in re mechanica abutuntur’.
| pag. 162. l. 11. Hinc sequitur, corpus A delapsum ex altitudine CD, praecise tantum acquisivisse virium, quantum corpus B lapsum ex altitudine EF. |
virium ascensionalium, nam si acquisitis celeritatibus sibi mutuo occurrant, non aequaliter resistunt. |
| |
| pag. 239. l. 4 à fine. Vita Wilh. BedelliGa naar voetnoot2) etc. |
Auctor Guil. Burnet. |
Note à l'article de Leibniz ‘De geometria recondita et analysi indivisibilium atque infinitorum’.
| pag. 295. l. 23. Quoniam etiam methodus investigandi Tetragonismos indesinitos aut eorum impossibilitates, apud me casus tantum specialis est (et quidem facilior) problematis multo majoris, quod appello Methodum Tangentium inversam, in quo maxima pars totius geometriae transcendentis continetur, et quod si Algebraice semper posset solvi, omnia reperta haberentur, et vero nihil adhuc de eo extare video satisfaciens, ideo ostendam quomodo non minus absolvi possit, quam Tetragonismus ipse indefinitus. |
magis. namtetragonismum indefinitum esse impossibilem. |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| Notes à un article sur celui de Cassini ‘Novae observationes circa Systema Saturni, habitae in observatorio regio Parisiis’ (lentibus Dn. Joannis Campani). |
| |
| pag. 470.l.2. Tertii distantia ab ansis maxima paulo major est diametro annuli: Revolutio vero circa Saturnum 4 dierum et 12½ horarum. Observatus hic est Telescopio Campaniano 34 pedum. |
Anno 1673 vid. Découvertes de 2 nou. Plan. |
| |
| ibid. l. 5. Quartus...revolutionem suam 16 fere diebus absolvit. Repertus hic est primum a Dn. Hugenio. |
Ao. 1655. |
| |
Année 1687.
Note à l'article de A.A. Kochanski S.J. ‘Mensurae universales magnitudinum ac temporum’.
| pag. 261. l. 5à sine. Nova mensura universalis magnitudinum. Praxis ad rem praesentem ita esset instituenda. Ex alterutura ala passeris masculi et senis, sumatur certa quaedam penna, v.g. tertia et quarta, et ea primum artificio facili in directum extendatur...etc...istae divisiones inservient nobis per modum scalae cujusdam artificialis...etc. |
Ineptiae! |
Note à l'article de Papin ‘Augmenta quaedam et experimenta nova circa antliam pneumaticam, facta partim in Anglia, partim in Italia’.
| pag. 325.l.18. CC est operculum antliae obliquo situ impositum. D foramen in summitate hujus operculi, valvula munitum... |
D debet esse prope C. |
Notes à l'article de Tschirnhaus ‘Additamentum ad methodum quadrandi curvilineas figuras, aut earum impossibilitatem demonstrandi per finitam seriem’.
| pag. 526.l.20. Hanc ergo ob causam in lunula hac non hujus solum spatii quadratura datur, sed infinitorum aliorum. |
Imo omnium. |
| |
| ibid. l. 24. 25. triangulum ABC semper aequabitur spatio lunulae BDE; et triangulum ACF, spatio FDE: quorum demonstrationem, ob facilitatem suam lubens hic omitto; quauqnam nesciam an ulli Theorema hoc animadversum fuerit, utcunque haec lunula multorum mathematicorum ingenia exercuerit. |
Baptistae Portae fuit animadversum cujus libellum habeo. |
| |
| |
| |
Année 1688.
Note se rapportant à l'article de Cassini ‘Epistola ad editorem Transactionum Anglicarum, exhibens ejusdem correctiones circa theoriam quinque satellitum Saturni’, translata e dictis Trans. Philos. M. Jun. 1687.
| texte de l'auteur. |
remarques de huygens. |
| |
| pag. 274. l. 22. Distantia satellitis secundi [note du traducteur: itidem a Cassino adinventi anno 1686] a Saturni centro... |
Ao 1684 puto ex literis Cassini ad me. |
Notes se rapportant à l'article de Jac. Bernoulli ‘Animadversio in geometriam Cartesianam, et constructio quorundam problematum hypersolidorum’.
| pag. 324. l. 1. Quae Regula a nemine hucusque in dubium vocata fuit. |
Imo à multis. |
| |
| ibid. l. 6, 7, 8, 9. Existimo namque, demonstratu haud difficile esse, quod cujuslibet generis curvae aptae sint ad construendas aequationes tot dimensionum, quot indigitat quadratum numeri dimensionum, ad quas ascendunt aequationes, curvarum illarum naturam exprimentes. |
vellem demonstrâsset. |
| |
| pag. 328. l. 11. priorem (quod cum Wallisio jam annotavi) continuari per AQ, posteriorem vero (quod a nemine hucusque observatum legi) per AS. |
observatum hoc in Horolog. Oscill. nostro Ao 1673. |
Note se rapportant à l'article de Fr. Jessop ‘Propositiones hydrostaticas ad illustrandum Aristarchi Samii Systema destinatae etc.’
| pag. 340. l. 6. Ex hujus fonte cum emanasse videret nobilissimus Auctor, quicquid pulchri, sani et sinceri admiramur in philosophia hodierna, indignatus neminem, excepto Robervallo et Mersenno, repertum, qui gratias illi rependerit, cui revera debeantur omnia, constituit methodice digerere principia illa, quibus nititur Systema Aristarchicum.. |
Systema hoc sub Aristarchi nomine à Robervallio confectum fuit. |
| |
Année 1689.
Notes se rapportant à la Pièce de Leibniz ‘Schediasma de resistentia medii, et motu projectorum gravium in medio resistente’.
De resistentia absoluta Artic. I: ‘Si motus mobilis sit per se uniformis et a medio aequaliter secundum spatia retardatus’.
| pag. 40. l. 21. Decrementa virium sunt proportionalia incrementis spatiorum; quae est hypothesis casus praesentis. |
celeritatum. |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| ibid. l. 27. sunt enim vires ut quadrata velocitatum. |
vires ascensionales. Sed his hîc nihil opus. |
| ibid. l. 29. elementa velocitatum amissarum sunt ut elementa spatiorum percursorum, residuarum ut adhuc percurrendorum. |
obscurum. |
| |
| ibid. l. 31. Ergo velocitates sunt ut spatia. |
non residua. |
| |
| pag. 41. l. 4. Si spatia residua sint ut numeri, tempora insumta erunt ut logarithmi, nam si elementa spatii sint progressionis geometricae, erunt spatia residua ejusdem progressionis geometricae, ergo etiam velocitates residuae, ergo incrementa temporis sunt aequalia, ergo tempora ipsa progressionis arithmeticae. |
Non apparet consequentia. |
Artic. II. ‘Si motus sit a gravitate acceleratus, et a medio aequaliter secundum loca retardatus’.
| ibid. l. antipen. Dantur rectae proportionales temporibus insumtis, a quarum unaquaque sidetrahatur recta aequalis respondenti spatio percurso a puncto mobili, residua recta erit... |
Quis haec intelligit? |
Artic. III. ‘Si grave projiciatur in medio resistentiam habente absolutam’.
| pag. 43. l. 9 seqq. sensus est, velocitates descensui adhuc deficientes, esse in ratione spatiorum adhuc limiti penetrationis deficientium, secundum aliquem numerum constantem multiplicata. |
Quis haec intelligit? |
| |
| ibid. l. 20. Inveniri potest linea projectionis AP, seu relatio inter coordinatas AG spatium descensus, et AM spatium progressionis per se uniformis. |
Hanc nos invenimus. Quidni et Author? |
Artic. IV. ‘De resistentia medii respectiva, si motus per se uniformis a medio uniformi retardatur proportione velocitatis’.
| ibid. l. 30. proportione velocitatis. |
duplicatâ. |
| |
| ibid. l. 33. Diminutiones velocitatum sunt in ratione composita velocitatum praesentium, et incrementorum spatii. Quae est hypothesis casus praesentis. |
Quid obscurius? Sunt ut quadrata velocitatum praesentium. Sunt enim ut resistentiae. Verum tamen dicit...incrementa spatii sunt ut velocitates. |
| |
| pag. 44. l. 14. Constans autem illa quantitas est tempus finitum, quo percurreretur spatium infinitum, si prima velocitas ea proportione cresceret, qua nunc a resistentia medii diminuitur. |
Nugae! |
Artic. V. ‘Si motus a gravitate acceleratus a medio uniformi retardetur proportione velocitatis’.
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| ibid. l. 21. retardetur proportione velocitatis. |
duplicatâ. |
| |
| ibid. l. 25. Resistentia est ad impressionem novam, a gravitate eodem temporis elemento factam... |
Pressio gravitatis statuitur semper eadem. |
| |
| ibid. l. 27...quadratum excessus velocitatis maximae... |
velocitatis acquisitae. |
| |
| pag. 45. l. 1, 2, 3, 4. Cum enim incrementum velocitatis sit differentia inter impressionem et resistentiam, hinc (ex praecedenti) statim sequitur impressionem esse ad incrementum velocitatis, ut quadratum velocitatis maximae ad excessum hujus quadrati super quadratum praesentis velocitatis assumtae. |
Sit sicut differentia; difficile est; videamus sequentia. Est tamen verum quod hîc dicit. |
| |
| ibid. l. 10. Velocitas maxima est talis exclusive, seu nunquam attingi potest, etsi ad eam intervallo inassignabili accedatur. Nam cum ratio est aequalitatis.... |
Ratio inter quid? |
| |
| ibid. l. 11, 12, 13, 14..seu cum velocitas assumta est incipiens sive infinite parva, tempus (adeoque logar.) est o, et proinde cum fit ratio infinita, hoc est, cum velocitas assumta est ipsamet maxima, logarithmus rationis est infinitus. |
Non potest intelligi. |
| |
| ibid. l. 19. Si velocitates acquisitae AV fig. 4 sint ut sinus (arcuum HK portionum quadrantis circularis HKB) erunt spatia percursa AS ut Logarithmi sinuum complementi VK... |
ut Logar. ration. contrariarum quadratorum sinuum complementi. |
| |
| ibid. l. 27, 28, 29. Patet hinc Logarithmum sinus totius esse o (cum velocitas est o) at evane scentis sinus complementi (cum velocitas est maxima) Logarithmum seu spatium esse infinitum, unde rursus patet velocitatem maximam nusquam attingi. |
Rursus obscurum. |
| |
| ibid. l. 5, 4, 3 à fine. Si spatia percursa AS fig. 4 sint ut Logarithmi sinuum KV, arcuum BK, tempora insumta sunt ut logarithmi rationum, quae sunt inter sinum versum BV et VD complementum ejus ad BD diametrum.... |
Hoc est si ut in casu velocitatum ang. sunt ut sinus. Hic rursus fallitur. Sunt enim temp. ut (½)½ logarithm. |
Art. VI. ‘Si grave projiciatur in medio uniformi resistentiam habente respectivam’.
| pag. 46. l. 6. 7. Sit fig. 4 projectio in AM et parallelis, descensus in AS et parallelis, angulo MAS quocunque; locus motus compositi P habetur completo parallelogrammo MASP. |
Nequaquam. |
| |
| |
| texte de l'auteur. |
remaques de huygens. |
| |
| ibid. l. 9 usque ad 22. Inveniri potest linea projectionis [Etc.]...Inveniri potest lineae tangens, seu ipsius mobilis in ea directio. [Etc.] |
Fallitur. |
| |
| ibid. l. 7 à fine. Omnia autem respondent nostrae Analysi infinitorum, hoc est calculo summarum et differentiarum. |
Sed non veritati. |
| |
pag. 47. l. 1.....mihi aliqua porro meditandi materia nota est, quam comprehendat περιάνδρου ϰλεάνϑ ς. ς. |
Non intelligo. |
Note se rapportant à la Pièce anonyme intitulée ‘La maniere de bien penser dans les ouvrages d'esprit, i.e. Ratio bene cogitandi in operibus ingenii’, Amstelodami, apud Abrahamum Wolfgang, 1688, in 12.
| pag. 111. l. 22, 23. |
Inter exempla illa commendatur illud Jani Vitalis epigramma, ad peregrinatorem quendam, qui Romam perlustrabat, directum: |
| |
| Aspice murorum moles praeruptaque saxa, Obrutaque horrenti vasta theatra situ. |
Quondam heic Roma fuit: nunc ipsa cadavera tantae |
| Haec sunt Roma: viden', velut ipsa cadavera tantae Urbis adhuc spirent imperiosa minas. |
Urbis adhuc spirant imperiosa minas. |
Note se rapportant à la Pièce de Papin ‘De gravitatis causa et proprietatibus observationes’.
| pag. 186, l. 7, 8, 9. Eadem facilitate resolvetur alia difficultas, ex proprietatibus gravium ascendentium desumpta, quae a Cl. Dn. Leibnitio proposita fuit in Act. Erud. mens. Maj. 1686, ubi ille contra Cartesium demonstrare nititur, vim motricem in corporibus a quantitate motus differre: ubi enim datur dupla quantitas motus, quadrupla ibidem vis motrix reperitur. |
Quaeritur de nomine tantum. |
Notes se rapportant à la Pièce de Papin ‘Examen machinae Dn. Perrault’.
| pag. 190, l. 14 à fine. A ponderibus AA circumgyrantur rotae B cum vecte CD, statim atque retinaculum in P solvitur: dictus vectis CD rotatione sua alliditur ad obicem in E, ibique sistitur. |
Non apparet quomodo. |
| |
| pag. 193. l. 10 à fine. ergo globus D cujus velocitas decupla est, poterit percurrere circiter 131 ped. dicto tempore 1″. |
Haec ita quoque forent si impedimenta negligeret et globus D sit 100. |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| ib. l. 8 à fine...illa velocitate, si nulla esset resistentia aeris, mobile posset ascendere ad altitudinem circiter 266 pedum. |
Nempe ex sententia Papini, sed errat. |
Note se rapportant à la Pièce de Leibniz ‘De linea isochrona, in qua grave sine acceleratione descendit, et de controversia cum Dn. Abbate De C[atelan]’.
| pag. 197. l. 3, 4, 5, 6, 7. Jam ratio TM ad TN eadem est quae velocitatis per curvam descendendi (seu horizonti porro in curva appropinquandi) quam grave habet positum in N, ad velocitatem qua idem ex N porro, non per curvam, sed libere descenderet si. posset. (ut constat ex natura motus inclinati). |
Quam miserè obscura haec omnia. |
Note se rapportant à la Pièce de Papin ‘Rotatilis Suctor et Pressor Hassiacus, in Serenissima Aula Cassellana demonstratus et detectus’.
| pag. 320. l. 18. Caeterum praeter utilitates hujus machinae superius recensitas, adjici etiam possit, quod illa pro praestantissimo folle facile inserviat.. |
vix credo. |
Note se rapportant à la Pièce anonyme ‘L'impiété des communions forcées etc. i.e. Impietas vi obtrusae communionis seu sacrae synaxeos demonstrata etc.’ Daventriae 1686, in 12.
| pag. 437. l. 12 à fine...neque Cardinalem Camum respondisse.. |
Camusium. |
| |
Année 1690.
Notes à l'article de Tschirnhaus ‘Methodus curvas determinandi quae formantur a radiis reflexis, quorum incidentes ut paralleli considerantur’.
| pag. 72. l. 1 et 2. Sit enim curva circularis AKDH et HE radius solaris incidens, fiat EG = EH, et FE sit dimidia ordinatim adplicatae CE, dico quod F sit punctum aliquod ex infinitis curvae IFD, ubi tangit eandem radius reflexus EG. |
Hanc constructionem ex meo libro de Luce sumsit. |
| |
| pag. 73. l. 9 à fine. Quam innumer a autem opticam perficientia inventa, eaque prorsus nova, hinc deduci possint..... |
Vellem unum adferret. |
| |
| |
| texte de l'auteur. |
remarques de huygesn. |
| |
| Notes à l'article de Tschirnhaus ‘Curva geometrica, quae seipsam sui evolutione describit, aliasque insignes proprietates obtinet’. |
| |
| pag. 169, l. 13 et 14. non ingratum eruditis me facturum putavi, si certiores ipsos facerem, eandem [proprietatem] a me in curva observatam fuisse non mechanica, in quarum censu cyclois habetur, sed cujus omnia puncta geometrice determinantur. |
Non se ipsam sed sibi similem. |
| |
| pag. 170. l. 20. theorema, quod de radio incidente et reflexo semper aequalibus cuidam curvae olim exhibui. |
Sed hoc theorema non demonstravit. |
| |
| ibid. l. 26. Jam vero quia in triangulis OPQ et OEC recta OP = OE, et angulus EOC = NOC = QOP, item angulus OEC = OPQ; patet reliqua quoque latera horum triangulorum inter se esse aequalia. |
Non ostendit QO et OC rectam lineam facere.... |
| |
| ibid. l. 29. Porro propter triangula similia OWQ et OEC, erit ut OC ad CE, sic OQ ad WQ. |
ergo nec hoc. |
| |
| ibid. l. ult. ang. WQO = OQP. |
Hoc non est ostensum. |
| |
| pag. 171. l. 12. Ego vero recensione illorum, quae citato loco videri possunt, lectori taedio esse nolo. |
Pendet ergo haec demonstratio à priori illâ. |
Une feuille séparée, trouvée par Jean Bernoulli dans le livre (‘intra folia reperi schedulam sequentia continentem’) donne encore sur l'article de Tschirnhaus les remarques suivantes qui nous obligent de reproduire les figures de Tschirnhaus.
Sit enim cum circulus ABC tangit CH in G, punctum describens in F, ergo quia arcus CF applicabitur ad arcum GH (hoc enim inde constat quod semicircumferentia ABC aequ. quadranti CGH) erunt arcus GH, GF aequales. Ergo ducta IGL, erit arcus FL, eoque et AB aequalis CG. Et quia AG aequ. CI, erit ang. CIG ad centrum aequ. ang. ACB ad circumf. hoc est ang. EGF sive KGI, ducta nempe recta FGK.
Non ostendit QOC esse lineam rectam, debuisset ducere rectam COQ quae cum tangente PQ alicubi concurreret in puncto Q. deinde quoniam ang. QOP = NOC, qui aequ. COE quia ON est reflexio radii EO, ostendere aequalitatem et similitudinem Δ orum QOP, COE, quia et latus OP = OE, et anguli utriusque ad O aequales. Hinc ergo OQ = OC cumque COQ sit recta linea, erit Q ad circumf. MG. Jam cadet QS perpend. in MC, eritque QS dupla OB, sive CE, sive QB. Unde curvae constructio
| |
| |
patet eadem quae curvae INF. Non consideravit in demonstratione punctum Q esse in circumf. MG cum tamen ita sit ex constructione. Pendet etiam demonstratio ex theoremate difficiliore quod non demonstravit quanquam verum esse ex mea demonstratione sciat.

| |
| |
| texte de l'auteur. |
remarques de huygesn. |
| |
| Notes à l'article de Leibniz ‘De causa gravitatis, et defensio sententiae suae de veris naturae legibus contra Cartesianos’. |
| |
| pag. 234. l. 17. Demonstrabo igitur propositionem, quam negat [objector], eaque occasione rem omnem (spero) in clara luce collocabo. |
non negat. |
| |
| pag. 235. l. 14. Ponamus jam porro, omnem potentiam globi A transferri debere in globum B. |
quomodo id fiet? |
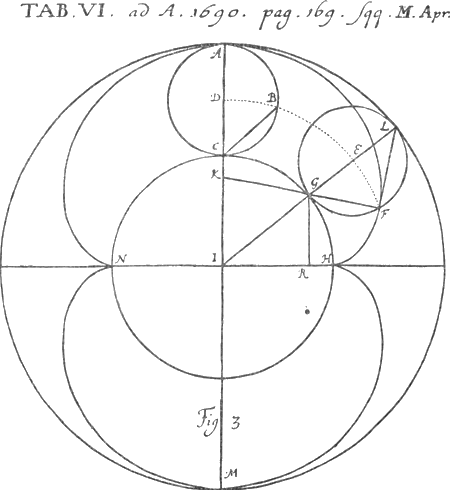
| |
| |
| texte de l'auteur. |
remarques de huygesn. |
| |
| ibid. l. 20. Cartesiani dicent..tantundem virium habere A, 4 librarum, celeritate ut 1, quantum B, unius librae celeritate ut 4. |
motûsGa naar voetnoot1) |
| |
| pag. 237. l. 11. Conclusimus contra Cartesianos, non semper debere conservari quantitatem motus. |
Hoc non negat Papinus. |
| |
| pag. 237. l. 7 à fine. At ego VIRES MOTRICES, id est eae quae conservandae sunt, ostendi non esse aestimandas gradibus celeritatis. |
Logomachia! |
| |
Année 1691.
Notes à l'article de Leibniz ‘O.V.E. Additio ad schediasma de medii resistentia (1689)’.
| pag. 177. l. 18. O.V.E. |
Quid hoc O.V.E. pro G.G.L.? |
| |
| ibid. l. 27. Animadverti autem eos [Hugenium et Newtonum] respectivam tantum (quam voco) resistentiam attigisse, qualem scilicet sentit corpus in liquido tenacitate notabili carente, velut in aere; non vero absolutam, quae oritur a tenacitate medii, aut asperitate... |
Imo maximè et hanc attigimus. |
| |
| ibid. l. 30..superficiei contactus attritum efficiente, inter quas multum interesse jam tum ostendi; cum respectiva habeat respectum ad celeritatem mobilis, eaque aucta crescat, absoluta non item. |
Imo crescit eadem ratione ac celeritas. |
Notes à l'article de Leibniz ‘Quadratura arithmetica communis sectionum conicarum quae centrum habent, indeque ducta Trigonometria Canonica, etc.’
| pag. 179. l. 6, 7. Et sane etiam in Opusculo nostro inedito nec ipso [Hugenio] viso, inter alias propositiones una continebatur satis memor abilis ob generalitatem, ambasque illas et plura complexa.. |
Bis affirmatur, sed miror cur non vulgaverit. |
| |
| pag. 181. l. 18. Huc usque res pervulgata est, sed ut ex iisdem differentia longitudinum calculo aestimetur, negotium est Geometriae transcendentis, quam pauci recte tractaverunt. Id ergo supplere nostrae methodi est. |
Sed absque hac supplevit Gregorius Scotus in addit. math. |
| |
| |
| texte de l'auteur. |
remarquès de huygens. |
| |
| pag. 182. l. 20. tangens anguli quem rhombus quaesitus facit ad meridianum, est ad sinum totum, ut arcus differentiae longitudinum est ad logarithmum hyperbolicum dictae rationis, seu ad e/1 + e3/3 + e5/5 etc. |
e - (e)/1 + e3 - (e3)/3 + e5 - (e5)/5 etc. |
Notes à l'article de Jean Bernoulli ‘Solutio problematis funicularii’.
| pag. 275. l. 10. Ducta tangente FD, erit AF. AD::BC. BF curvam. |
Idem ex meis: sed ego et hoc, nempe quod DF-AF ad AD ut AB ad BF curvam. |
| |
| ibid. l. 12. Curva BE vel BF aequalis est rectae AG.. |
Idem ex meis. |
| |
| ibid. l. 20. Recta BM usque ad principium curvae MNO sumta aequatur ipsi CB. |
Idem ex meis, sed insuper quod DF-FA ad FA ut AB ad BM. |
| |
| ibid. l. 22. MP est dupla ipsius BA. |
Idem ex meis verum. |
| |
| ibid. l. 24. Recta CP bisecta est in puncto A. |
Idem ex meis. |
| |
| ibid. l. 25. Curva EB est ad curvam MNO, ut recta CB ad rectam AG. |
Idem ex meis. |
| |
| ibid. l. 26, 27, 28, 29, 30, 31. Si ad AG applicentur duo rectangula AI, AK, quorum unum AI ei quod sub semilatere transverso CB et recta FG comprehenditur rectangulo, alterum AK quod ipsi spatio hyperbolico BGA aequatur; et differentia latitudinum KJ sumatur in axe a vertice B aequalis BL, erit punctum L centrum gravitatis curvae funiculariae EBF. |
Verum; sed ex meis breviter, ponendo tantum AL = GK. |
| |
| ibid. l. 32 etc. Si super EF infinitae intelligantur descriptae curvae ipsi funiculariae EBF aequales, illaeque in rectas extendantur et in singulis singulae extensae punctis applicentur rectae ipsis respective distantiis a linea EF aequales, erit omnium spatiorum quae sic efficiuntur illud quod a funicularia gignitur maximum. |
Non intelligo quid velit, nisi quod centrum gravitatis curvae pendentis quam humilissimum sit (rem acu tetigisti) melius dixisset (tibi quidem sed non sibi) si super EF quaelibet alia curva describatur funiculariae aequalis et in partes totidem aequales dividatur, deinde utraque extendatur in rectum et in singulis etc. cuique suum pulchrum est. |
| |
| |
| texte de l'auteur. |
remarquès de huygens. |
Ici (dernière remarque de la page précédente) nous rencontrons pour la première fois dans les notes des mots soulignés. Korteweg qui a copié les notes croit pouvoir affirmer qu'il s'agit ici de mots ajoutés par Jean Bernoulli aux remarques de Huygens. Ceci s'applique aussi aux mots soulignés dans les remarques qui suivent. Nous imprimons tous ces mots en italiques.
| ibid. infra columnam [c.à.d. après les lignes citées plus haut]. |
Nihil habet de superficie conoidis FBE. Haud dubie habuisset si de eo cogitâsset sed tu Hugens nihil habuisti de reductione funiculariae ad spatium hyperbolicum quia ipse fater is tuam methodum eò non pertigisse. |
Notes à l'article de Leibniz ‘De linea in quam flexile se pondere proprio curvat ejusque usu insigni ad inveniendas quotcumque medias proportionales et logarithmos’.
| pag. 278. l. 6. Linea sic construitur geometrice, sine auxilio fili aut catenae, et sine suppositione quadraturarum.. |
Imo suppositâ quadratura hyperbolae, ut ipse fatetur in actis 1691 pag. 436. |
| |
| ibid. l. 10...qua ratione semel cognita..... |
Imo oportet ex logarithmis hanc rationem petere quia ponitur ☉ 3 N = ☉ A. |
| |
| l. 6 à fine...si quaeratur logarithmus rationis inter ☉ A et ☉ ω. |
Sed quomodo invenitur ☉ A? non nisi per logarithmos. |
Note à l'article de Huygens lui-même ‘Solutio ejusdem problematis’.
| p. 282. l. 11. Quadratura autem hujus curvae pendet a summis secantium arcuum per minima aequaliter crescentium. |
Ad maximum eorum arcuum applicata. |
Notes à l'article de Jacques Bernoulli ‘Specimen alterum calculi differentialis in dimetienda spirali logarithmica loxodromiis nautarum, et areis triangulorum sphaericorum: una cum additamento quodam ad problema funicularium, aliisque’.
| pag. 283. l. 11, 12. Quia spiralis haec infinitis gyris circa centrum C convolvitur, patet, curvae alicui interminatae posse rectam finitam aequalem dari. |
Imo patet curvam infinitè crescentem quamlibet propè aequari rectae finitae. |
| |
| ibid. l. 14. Positis CB = r, CH = t, BM = x, CE = y. |
y non tantum CE significat sed DC, EC, LC. |
| |
| |
| texte de l'auteur. |
remarquès de huygens. |
| |
| ibid. l. 16. et hujus integrale tyy/4r = omnibus triangulis FCE, GCI, etc. |
Ad inveniendum hoc integrale considerandum y indefinitum, unde ty/2r sunt applicatae in triangulo, cujus basis maxima y, altitudo est maxima ty/2r. |
| |
| ibid. l. 10 à fine..erit tyy/4r = toti spatio spirali BDPCB, repetitis videlicet toties portiunculis circa centrum G existentibus, quot gyris singulae communes sunt. |
Hoc modo nulla certa quantitas designatur, verum spatium est quod comprehenditur à radio et curvae parte quae peripheriae respondet. |
| |
| pag. 284. l. 12. zdx/r. dy∷t. r. |
seu ut EF ad FD in fig. I. |
| |
| ibid. l. 14. dx = trdz/2√rr-zz |
Hoc utile ad dimens. spatii vid. fig. 286. |
| |
| ibid. l. 15. Applicetur extremitati radii AC normalis CP = t... |
NB. CP = t uti et Bρ. |
| |
| ibid. circa finem. ideoque spatium hoc applicatum ad radium exhibet rectam aequalem arcui aequatoris, qui differentiam longitudinum exhibet puncti B... |
Haec nihili sunt, cum obscurum per obscurius explicent. |
| |
| pag. 285. l. 6. differentia longitudinum duorum locorum est ad differentiam duorum aliorum latitudine cum prioribus convenientium, ut tangens anguli prioris rumbi ad tang. ang. post. |
Hoc alia simplici demonstratione probari potest. |
| |
| ibid. l. 21. spatium curvilineum δγπρ... |
Sed quomodo cognoscitur spatium δγπρ? |
| ibid. l. 24. trdy/z = rdx |
v. pag. 284. l. 14 ubi dy = zdx/t |
| |
| pag. 286. l. 9...pzdz/√rr-zz aream annuli DE, ejusque integrale p √rr-zz... |
Nam zdz/√rr-zz = FE, omnia autem FE = GA seu √rr-zz, z indefinitè accipitur pro quavis DG. |
| |
| ibid. l. 16. |
pag. 284. l. 15. |
| |
| ibid. l. 17. dx √rr-zz = areae trapezii sphaerici, cujus bases oppositae sunt differentiolae arcuum aequatoris et paralleli. |
ut LMEF in fig. I. |
| |
| |
| texte de l'auteur. |
remarquès de huygens. |
| |
| ibid. l. 19 est vero integrale ipsius trdz/z = spatio hyperbolico. |
Hoc egregium: nam si fiat ut DG sive AL ad AB ita Bρ ad aliam, ea erit LM = tr/z quae ducta in dz sive VL facit trdz/z = □ VLMat omnia □ VLM faciunt spatium hyperb. pBVr. Ergo trilineum sphaericum ut BCE in fig. I aequatur differentiae inter circulum et portionem hypb. |
| |
| pag. 287. l. 1...sequitur reliquum TprX aequari ipso spatio, utroque meridiano, loxodromica et polo terminato. |
Hoc rursus nihili facio [quia?]ignotum sp. TprX. |
| |
| pag. 289. l. 2 et 3. Additamentum ad problema funicularium [quelques formules]. |
Haec nihil habent elegantiae. |
| |
| ibid. l. 13 à fine. Ego per solutionem casus simplicissimi (saltem in praememorata hypothesi extensionis) adyta Problematis feliciter reseravi. |
Vereor ne falsum vel incertum quid ponat pro hypothesi. |
| |
| pag. 290. l. 5, 6, 7. Qui naturam pressionis fluidorum intellexerit, haud difficulter quidem capiet, quod portio veli BC, quae subtensam habet directioni venti DE perpendicularem, curvari debeat in arcum circuli. |
Absurdum hoc quidem. |
Notes à l'article de Jacques Bernoulli ‘Demonstratio centri oscillationis ex natura vectis, reperta occasione eorum, quae super hac materia in Historia Literaria Roterodamensi recensentur’.
| pag. 319. l. 13 et seqq. usque ad medium paginae sequentis.....distributio seu translatio quantitatis motus (olim solas celeritates consideravi, quia pondera supposui aequalia) nihil obscuritatis habere tandem potest.........G fore centrum oscillationis quod itaque repertum est. |
Haec omnia absurda sunt et per consequentias parum evidenter demonstrata. |
| |
| pag. 320. l. ultimâ in liquidis enim res magis dubia videtur; cum vix appareat, quomodo cum ista hypothesi conciliari possit spontaneus communis centri gravitatis ascensus, qui accidit, cum metallum in imo liquoris acidi positum ac dissolutum, aut liquor levior graviori leniter superinfusus eidem sensim permiscetur; id quod ansa et fundamentum extitit Perpetui Mobilis nuper a Fratre inventi ac in Actis publicati. |
Facile ratio redditur ex motu particularum acidi, qui motus oritur à motu materiae subtilissimae de qua in libro de causâ gravitatis egimus. |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
Note à l'article de Leibniz ‘De solutionibus problematis catenarii vel funicularis in Actis Junil A. 1691 aliisque a Dn. I.B. propositis’.
| pag. 437 l. 9. 10. Ubi vero [Jacob Bernoullius] videbit, quomodo res ista [il s'agit de la loxodromique] reducta sit ad quadraturam hyperboloe aut logarithmos, agnoscet credo..... |
Sed et multo ante à S. Gregorio. |
Note à l'article de Leibniz ‘De legibus naturae et vera aestimatione virium motricium contra Cartesianos responsio ad rationes a Dn.P.[Papin] mense Januarii proximo in Actis hisce propositas’.
| pag. 440. l. 7.....quoniam si illud unam libram possit elevare ad pedes 4.... |
[si illud] 4 libras ad pedem 1 seu [unam libram etc.]. |
| |
Année 1692.
Notes à l'article de Jean Bernoulli ‘Solutio curvae causticae per vulgarem geometriam Cartesianam, aliaque’.
| pag. 32. l. 21. resid. ☽ |
Jam habet z simplex [il s'agit d'une équation qui contient z au premier degré seulement]. |
| |
| ibid. l. 23 ☿ 6xz3...= 0 |
Aggreditur investigare alterum valorem z. |
| |
| ibid. l. 3 à fine resid. ♀ |
Habet rursus z simplex. |
| |
| pag. 33 l. 3. Multipl. per crucem et reducta oequatione ad cyphram orietur tandem... |
Hic eliminatur jam z. |
| |
| ibid. l. 4, 5, 6, 7. 64 x6 - 48aax4 + 12a4xx - a6 + 192yy - 96aayy - 15a4yy + 192y4 - 48aay4 + 64y4 = 0. |
Aequatio curvae causticae. |
| |
| ibid. l. 11...unde consequitur, diversam esse ab ea, quam applicatae semicirculi in punctis bisectionum formant... |
Quae erat Tschirnhausii paralogisticè inventa. |
Note à l'article sur le livre de John Ray ‘The wisdom of God manifested in the works of the creation’ (sive ‘Sapientia Dei manifestata in operibus creationis’), Londini, apud S. Smith, 1691.
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| pag. 81. l. 4, 5 à fine....Ne vero quis forte hanc corporis erectionem arte potius superinductam nobis concipiat, quam a provida Natura destinatam...Noster pluscula producit argumenta, quae contrarium evidenter evincant. Primo enim urget nimiam inaequalitatem longitudinis brachiorum atque crurum, unde homo si non penitus incapax, saltem inter omnes quadrupedes maxime ineptus ad pronum incessum reddatur.. |
Non magis quam simia. |
Notes à l'article de Jacques Bernoulli ‘Additamentum ad solutionem curvae causticae fratris Jo. Bernoulli, una cum meditatione de natura evolutarum, et variis osculationum generibus’.
| pag. 113. l. 9 à fine...fit ut si [parabola] quam curvam secundo, nonnunquam etiam primo tantum gradu osculatur, jam complete osculetur: uti recta quamcunque tangit, complete tangit. |
Circulus quamcunque curvam osculatur completè osculatur. |
| |
| pag. 115. l. 24. Ita semiparabola cubica...non potest unius solius curvae evolutione tota describi, sed requiruntur duae..... |
Eadem scripsi in lib. de Evolutione Curvarum. |
| |
| pag. 116. l. 4 à fine. in omni enim flexu contrario circulus osculator abit in lineam rectam, fit radii infinite magni. |
Fallitur. |
Notes à l'article de Jacques Bernoulli ‘Curvatura veli’.
| pag. 202. l. 15, 16. sed neque haec [directio juxta quam velum a vento impellitur] determinari potest, nisi ipsa veli curvatura comperta habeatur, adeo ut totius negotii certitudo tandem in cognitione figurae veli terminetur... |
totius negotii. Nugae! |
| |
| pag. 203. l. 10. Agnoscit hac in parte imperfectionem Artis Anonymus Gallus [Renau] sub finem libelli egregii quem ‘de la Theorie de la Manoeuvre des Vaisseaux’ inscriptum ante paucos annos jussu regio edidit. |
sed pleni paralogismis. |
| |
| ibid. l. 21. Si subtensa veli EBF, hoc est, per extremitates veli ducta recta EF lineae directionis venti AB perpendicularis est arcuatur velum in Circuli segmentum... |
Ubi igitur funicularia? |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| ibid. l. 29. Celeritas navium eodem secundo vento velitantium, caeteris paribus, sunt ut velorum subtensae. |
celeritas navium. Errat; imo sunt in ratione subdupla velorum subtensorum. Ita enim fiunt resistentiae sicut vires impellentes. |
| |
| pag. 204. l. 5, 6, 7, 8. Porro si velum EGB super extremitatibus suis E et B ita sit expansum, ut per extremitatem B directioni venti AB ducta perpendicularis recta BD tangat velum in B, curvatur velum in Funicularium, cujus vertex B, axis AB. |
Falsum. |
| |
| pag. 205. l. 5 à fine. Si veli denique extremitates sint E, B, et ex B ducta recta BG, directioni venti perpendicularis, secet velum in G, curvatur ejus portio GB in circulum, altera EG in funicularium. |
Absurdum. |
| |
| pag. 206. l. 10, 9, 8 à fine. Ego interea pro homine mediterraneo ad negotium maritimum, quo non est aliud e quoquo rebus humanis major accedit utilitas, plus satis contulisse mihi videor. |
Imo haec nullius usus essent, etiamsi vera. |
Notes à l'article de Leibniz ‘Constructio testudinis quadrabilis hemisphaericae’ (p. 275-279).
| In Tab. V... |
Melius carbasum invenisset ponendo KB = SF vel FΣ item. Puncta curvae ex rectis ungulae ordinantur. |
| |
| pag. 279. l. 13, 14..Si sit PB aequ. KF, aequabitur iterum carbasus quadrato radii. |
aequabitur dimidio. Hîc erraverat ut monuit Jac. Bern. corrigit ea in Actis Ai 1693. p. 42. |
Note à l'article de Jacques Bernoulli ‘Additio ad schedam de lineis cycloidalibus etc.’
pag. 296. lineae undecim ultimae.
...cum contra Spirae mirabilis caustica in speculum mutata, et radios ex communi umbilico emanantes repercutiens, aliam non minorem sed identicam prorsus Spiram producat. Quemadmodum itaque per productionem Spirae mirabilis communicationem essentioe divinae ad intra (ut in Scholis loqui amant) qua Deus Filius Patre non minor, sed aequalis ex intima Patris essentia et Deitatis quasiumbilico nascitur, et ab utroque exit Spiritus S. utriq: par, non |
O Ineptiae! et quidem enthusiasticae [comme il a été dit à la p. 802 qui précède, |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| inconcinne adumbrari nuper partim diximus: ita nunc continuata analogia communicationem imaginis divinae ad extra, qua Creator ex infinito quasi intervallo, (quo a Creaturis suis distat) ipsis radios divinitatis impertit, eo vero imperfectiores minoresque, quo minus immediate ad nos emanarint, per Cycloidis productionem non minus apte repraesentari posse arbitramur. |
les mots soulignés ont apparemment été ajoutés par Jean BernoulliGa naar voetnoot1)]. |
| |
Année 1693.
Note à l'article sur le livre de Erhard Weigel ‘Philosophia mathematica, theologia naturalis solida, per singulas scientias continuata, universae artis inveniendi prima stamina complectens’, Jenae, M. Birkner, 1693.
| pag. 216, l. 5. Erhardi Weigelii...etc. [titre du livre]. |
Vidi et conveni hunc AuthoremGa naar voetnoot2) qui erat senex nugivenditor mathematicae scientiae imperitus. |
Note à l'article de Jean Bernoulli ‘Solutio problematis Cartesio propositi Dn. de Beaune’. Vide Cartesium Epist. 79, tom. 3.
| pag. 234. l. 5. Prima mea hujus problematis solutio, quae reperitur tecto nomine in Diario Gallico 34. anni elapsi..... |
Hospitalius istam solutionem sibi vindicat, sed perperam. |
| |
| ibid. l. 8 à fine. Solutio: Ad asymptoton AB perpendicularem ad AK construatur logarithmica vulgaris DC.. |
Hospitalius meliorem constructionem ad me misit 12 febr. 1693. for san non suam. |
| |
| |
Note à l'article de Jacques Bernoulli ‘Curvae diacausticae, earum relatio ad evolutas, aliaque nova his affinia. Item: Natura osculorum obscurius explicata. Celeritates navîum definitae. Regula pro resistentiis, quas figurae in fluido motu patiuntur etc.’
| texte de l'auteur. |
remarques de huygens. |
| |
| pag. 252. l. 11. Primo enim si pars superficiei prorae immersa aquis plana statuatur et aequalis subtensae veli seu basi segmenti circularis, quod velum refert, et insuper ratio gravitatis aeris ad gravitatem aquae ut 1 ad 841, illi, quae natura obtinet, quam proxime conformis, deprehendo, velocitatem navis maximam, cujuscumque caetera molis sit, praecise fore subtrigecuplam velocitatis ipsius venti, nisi quod ponderosior navis tardius hanc velocitatem assequatur. |
Ita est. |
Note à l'article de Leibniz ‘Ad problema Majo nupero in his Actis p. 235 propositum’.
| pag. 313. l. 13. Perplacet problema Bernoullianum nupero mense Majo propositum, de invenienda linea ABC ex data ratione inter tangentem BD et resectam AD ex axe AE, per tangentem. |
Nescio an solverit problema, etfi vult videri solvisse. |
| |
| ibid. l, 12 à fine. Itemque locum habet [nostra methodus differentialis] in aliis innumeris, ut si detur ratio dictae resectae AD, ad ordinatam BE. |
Hoc longe facilius est et factum habemus. |
Notes à l'article de Leibniz ‘Supplementum Geometriae Dimensoriae, seu generalissima omnium tetragonismorum effectio per motum: similiterque multiplex constructio lineae ex data tangentium conditione’.
| pag. 385. l. 5 Supplementum Geometriae... |
Speciosus titulus in re nihili. |
| |
| pag. 388. l. 10. Nec difficile mihi fuit deprehendere, hujus lineae descriptionem ad quadraturam hyperbolae revocari posse. |
Il credere e cortesia. |
| |
| ibid. l. 22. Cum igitur figurae tangentium area exhiberi possit per quadraturam hyperbolae vel logarithmos, ut notum est... |
Notum paucis sed a nemine adhuc ostensum. |
| |
| pag. 389. l. 5 à fine. Cum ergo constructionem repererim, generaliter sese extendentem ad omnes quadraturas... |
Nihil tamen profuturam, praeterquam in unâ illa quadratrice nostrâ, atque ibi vix etiam. |
| |
| pag. 390. l. 12 ad 3 à fine. [C'est un passage appartenant au ‘problema generale quadraturarum’ que Leibniz dit pouvoir ‘reduci ad inventionem lineae datam habentis legem declivitatum’]. |
Obscurum! |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| pag. 391. l. 18. Punctum vero describens seu stylus C ante se protrudat HR, regulam, in eodem plano horizontaliter ad AH...incedentem, versus A; quoe protrusio non impedit... |
Imo maximè impedit. |
| |
| ibid. l. 23. Denique in hac tabula sit descripta...linea rigida EE... |
Haec omnia intellectu difficillima et cum intellexeris nequaquam effici possunt. |
| |
Année 1694.
Notes à l'article de Jac. Bernoulli ‘Curvatura laminae elasticae. Ejus identitas cum curvatura lintei a pondere inclusi fluidi expansi. Radii circulorum osculantium in terminis simplicissimis exhibiti etc.’
| pag. 265. l. 12 à fine. Esto spatium rectilineum sive curvilineum quodvis ABC fig. 2, cujus abscissoe AE vires tendentes, ordinatoe EF tensiones repraesentent... |
Quomodo has tensiones et vires tendentes in lamina sua considerat aut filo intorto. Si legem extensionis ad vires tendentes certam non ponit, non video quidquam definiri posse de curvaturâ. |
| |
| ibid. l. 6 seqq. à fine. Erit punctum N ad curvam quandam AN talem, ut si spatio AEN pergas statuere aequale □ lum AO, rectasque OP, FE producas ad communem occursum in Q, existat punctum Q in curva optata AQR. |
Ignota nempe est curva ignotaque magis ejus quadratura, qua hic opus haberemus. Ergo nihil efficit. |
| |
| pag. 266. l. 1 seqq....firmetur una extremitate in RS ad perpendiculum, alterique AV potentia applicetur, sive pondus appendatur z....etc.......acquiret concava laminoe superficies RQA curvaturam quam construximus.. |
Nihil probat, nec dicit qua lege laminas curvari ponat. |
| |
| ibid. l. 16. Si lamina inflexa RQA loco puncti R firmetur alicubi in Q, resecta portione RQ, servabit reliqua ab eadem potentia inflexa eandem curvaturam AQ. |
Dubito. |
| |
| pag. 267. 1 seqq. Eadem quoque curvatura AQa gaudere consentaneum est Assulas illas, ex quibus Dolia confiunt... |
Non habet rectanguli figuram. |
| |
| pag. 272 l. 15. Ducta Tangente Qp, erit subtangens Pp quarta proportionalis ad AB, AE et EN. |
Haec et sequentia non proderunt, si ponatur natura elateris ordinaria. |
| |
| |
| texte de l'auteur. |
remarques de huygens. |
| |
| pag. 275. l. 19-26...excutietur haec portio a pondere inclusi fluidi juxta eam directionem, quoe...etc.... |
Ô NUGAS! |
| |
| pag. 277. l. 15. Plenariam vero illius solutionem, sive constructionem, nec ipse [frater] nec quisquam alius dare potuit. |
Forsan dare potuissent qui non quaesiverunt. |
| |
| Note à l'article de Leibniz ‘Nova calculi differentialis applicatio et usus, ad multiplicem linearum constructionem, ex data tangentium conditione’. |
| |
| pag. 316. l. 7. Solutionem suam Problematis Bernoulliani mense nupero Majo...Actis Eruditorum insertam, Dn. Marchio Hospitalius Autor defendere non distulit...Nostra autem nova... |
Tuam tamen solutionem ejus problematis non vidimus. |
Notes à l'article de Leibniz ‘Constructio propria problematis de curva isochrona paracentrica. Ubi et generaliora quaedam de natura et calculo differentiali osculorum, etc. etc.’.
| Pag. 365. l. 20, 21, 22, 23, 24, 25, 26, 27. Tale hoc est...radius osculi est ad unitatem ut elementum unius coordinatoe est ad elementum rationis elementorum alterius coordinatoe et curvoe. Rationem autem hic sumo pro re homogenea unitati vel numero, quoe ori tur ex divisione antecedentis per consequens. Item: distantia centri osculantis circuli ab ordinata curvoe, est ad unitatem, ut tertia proportionalis elementorum abscissoe et curvoe est ad elementum rationis elementorum abscissoe et ordinatoe. |
Quanta obscuritas! |
| |
| pag. 371. l. 7, 8. elementa spatior. Sunt autem (ex generalissima motus lege) elementa spatiorum in ratione composita velocitatum et temporis elementorum. |
Verum est. |
| |
| ibid. l. 10. Porro ex lege motus gravium velocitates sunt in duplicata ratione altitudinum HB. |
subduplicata. |
| |
| bid. l. 13. fiet vv ut a + x... |
poterit ergo √a + x pro celeritate sumi. |
| |
| pag. 373. l. 9. Tantum vero ipsius [il s'agit de Jacques Bernoulli] acumini et profundae harum rerum notitioe tribuo, ut quod rite expressa meisque rationibus consideratis secunda meditatione statuet, plurimum apud me ponderis sit habiturum. |
ergo tunc calculum tuum nihili esse fateberis? hoc enim sequitur, ergo jure nunc dubitas. |
|
-
voetnoot1)
- Nous imprimons en italiques les lignes indiquées par Jean Bernoulli.
-
voetnoot2)
- The life of William Bedell, D.D. Bishop of Kilmore in Ireland, Londini, apud J. South by, 1685 in 8.
-
voetnoot1)
- On voit bien ici la différence des tournures d'esprit de Huygens et de Jacques Bernoulli sur laquelle nous avons aussi attiré l'attention dans notre publication de 1945 ‘De kromme van Joh. Bernoulli volgens Chr. Huygens en anderen’. Huygens ne partage en aucune façon l'enthousiasme mathématico-biblique, mystique, de Jacques Bernoulli souligné ici par son frère et qui rappelle plus ou moins celui de Kepler. Voyez aussi ce qui a été dit sur le mysticisme à la p. 407 qui précède.
|

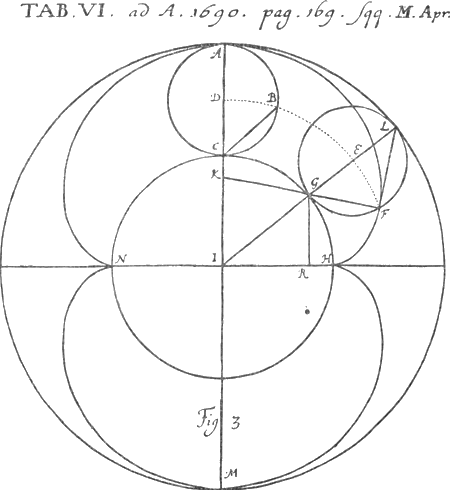


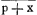
 ς.
ς.