Oeuvres complètes. Tome XXII. Supplément à la correspondance. Varia. Biographie. Catalogue de vente

[p. 497]

Séjour et travaux à la Haye de décembre 1655 à octobre 1660.

[p. 499]

Sejour et travaux à la Haye de décembre 1655 à octobre 1660.

Le père Constantyn avait exprimé la pensée que Christiaan reviendrait de Paris bien changé. Il est vrai que nous ignorons en quels termes il l'avait dit, lui qui vantait les qualités extraordinaires de son fils depuis longtemps¹⁾. Christiaan n'admet cette transformation que dans une certaine mesure: ‘pour ce qui est du sejour de Paris, je croy bien que tant que j'y demeurerai d'avantage et plus je profiteraij de la conversation des gens de cette nation, mais pour revenir tout autrement faict que je n'estois en partant, je ne scay si l'on le jugera. pour moy je ne m'appercois pas de ce changement, du quel il en est peut estre de mesme, que quand on croît en grandeur²⁾’. Ce qui est certain c'est qu'il pouvait désormais correspondre - comparez la p. 496 - avec quelques connaissances personnelles distinguées à Paris: Chapelain, Mylon, Roberval, Conrart, Mocchi, Boulliau (avec aucun desquels il n'avait été en correspondance avant ce temps). Chapelain, ayant bientôt reçu de lui un certain nombre des petites brochures ou feuilles nouvellement imprimées sur le satellite de Saturne³⁾ lui parle de différentes Assemblées, académiques et autres, où il les distribua ou en fit la lecture, laquelle fit grande impression surtout par l'annonce d'un ouvrage sur le système entier de la planète; il écrit e.a. combien de Montmor, que Christiaan n'avait pas vu, s'y intéresse.

Chapelain paraît avoir causé avec Gassendi encore après la visite de Christiaan, puisqu'il dit⁴⁾: ‘Vous aués perdu un grand admirateur en feu Monsieur Gassendi, qui faisoit déjà grand cas de vous’.

Les années 1656-1660 nous semblent être celles où Huygens déploya la plus grande activité. Sa santé laissa sans doute peu à désirer. Il est vrai qu'en septembre 1656 il dit avoir été incapable de travailler pendant quelque temps⁵⁾; ce fut, nous

1) Présent Tome. p. 57.

2) T.I. p. 356.

3) T. XV, p. 173-177.

4) T.I. p. 483, août 1656.

5) T.I. p. 495.

[p. 500]

semble-t-il, une interruption d'un mois. Cette activité se manifesta aux yeux de tous, outre par la petite brochure mentionnée, par l'apparition en 1656 de la lettre à Ainscom sur la prétendue quadrature du cercle⁶⁾, du Traité sur le Calcul dans les jeux de hasard, d'abord en latin⁷⁾ en 1657, puis en néerlandais en 1660, de l' ‘Horologium’ en 1658, de quelques contributions à la nouvelle édition de 1659 de la Géométrie cartésienne par van Schooten, et surtout par celle, en cette même année 1659, du ‘Systema Saturnium’⁸⁾, suivi en 1660 par la ‘Brevis assertio Systematis Saturnij’.

Mais en outre il continua à s'occuper de la théorie du choc des corps - voyez dans le T. XVI⁹⁾ l'esquisse d'une préface et quelques appendices intéressants de 1656 - de la taille de lentilles et de la construction de lunettes, de diverses questions de mathématique pure autres que celles du partage de l'enjeu dans le cas de jeux de hasard non terminés. Il rassembla de plus des observations sur les couronnes et parhélies et s'occupa de la théorie de ces phénomènes, mesura ce que nous appelons l'accélération de la pesanteur¹⁰⁾, considéra avec attention, en rapport avec la mesure du temps par les horloges, l'inégalité des jours, trouva la longueur d'un pendule mathématique isochrone avec un pendule portant deux poids, ainsi que la forme des ‘joues’ (pour parler avec les anglais qui disent ‘cheeks’) capables de rendre isochrones les oscillations grandes et petites d'un pendule mathématique donné, construisit l'horloge à pendule conique avec de pareilles lames correctrices pour les oscillations d'amplitudes diverses, et réussit à calculer la grandeur de la force centrifuge comparée à celle de la pesanteur. C'est à bon droit qu'il écrit à Colvius: ‘Occupatior fum mi Colvi quam fortasse credideris¹¹⁾’. Dans les ‘Varia’ du présent Tome on trouvera aussi une figure se rapportant à la lanterne magique, des considérations sur le mécanisme de l'articulation, des figures fantastiques d'une sandale à ressort et d'un marcheur sur l'eau supporté par des bassins ou souliers aquatiques. Nous avons dit plus haut¹²⁾ que les frères Huygens pratiquèrent e.a. (il est vrai qu'il n'en est parlé qu'une seule fois) le sport national du patinage; faut-il croire à un lien mental entre les patins

6) Voyez la p. 443 qui précède.

7) Traduction du néerlandais.

8) Voyez sur les observations astronomiques (où il y en a aussi qui datent de 1655) la p. 7 du T. XV.

9) P. 137-155.

10) T. XVII, p. 278 et 281. Huygens parle (T. V, p. 150) de ‘la proportion certaine de l'accroissement des vitesses’.

11) T. I, p. 470, juillet 1656.

12) P. 402. Le père Constantyn parle des deux frères aînés.

[p. 501]

et les dits souliers et sandales? Ailleurs Huygens parle, en 1658, de voler en faisant aller des ailes au moyen d'air comprimé¹³⁾.

Dans les mêmes ‘Varia’ on a pu voir une traduction de l'anglais d'une visite aux pyramides de l'Égypte et plusieurs citations de récits de voyage - il y en avait dans la bibliothèque du père Constantyn - d'autres visiteurs de ces célèbres monuments.

Ce n'est pas l'un après l'autre que ces sujets furent traités par Huygens. Le Manuscrit A, premier des grands livres manuscrits - il avait compris depuis longtemps qu'il n'y a pas lieu de se servir uniquement de feuilles séparées, mais les manuscrits antérieurs sont de plus petites dimensions - dont la première page porte la date du 7 avril 1658, débute par trois pages sur les couronnes et parhélies¹⁴⁾, la quatrième traite de la parabole cubique¹⁵⁾, la cinquième porte le premier dessin que nous possédions - ébauche grossière - d'une horloge avec pendule et fourchette¹⁶⁾: viennent ensuite quelques pages sur l'inégalité des jours¹⁷⁾ etc. Cette suite désordonnée - quoiqu'assurément il y ait un lien mental entre les deux derniers sujets mentionnés - est de règle aussi pour les manuscrits suivants jusqu'au dernier qui porte la lettre I. Il y a en vérité encore le grand manuscrit K, mais celui-ci, qui contient e.a. des copies de pièces antérieurement écrites, observations etc., ne fait pas partie de la série¹⁸⁾.

On ne trouve dans ces manuscrits que des dates espacées; il serait donc impossible en général, même s'il n'y avait pas en outre un grand nombre de feuilles séparées, de suivre les pensées de Huygens de jour en jour. Là où l'on pourrait y réussir, pareil traitement minutieux serait néanmoins fastidieux et pire qu'inutile; le lecteur, pour nous servir d'une locution néerlandaise, ne verrait plus de bois dans cet amas d'arbres.

C'est à grouper les pages manuscrites dans un ordre raisonnable - souvent historique dans les détails - que nous nous sommes appliqués dans les Tomes précédents¹⁹⁾. Dans le présent Tome l'ordre historique nous intéresse avant tout ou, pour

13) T. XVII, p. 307.

14) Voyez l'Appendice II aux p. 451-456 du T. XVII.

15) Voyez la parabole cubique, d'après une autre page du Manuscrit A, à la p. 395 du T. XIV dans le Recueil ‘Travaux mathématiques divers de 1655 à 1659’.

16) Nous avons reproduit cette figure à la p. 74 du T. XVII.

17) Consultez sur des pages ultérieures du Manuscrit A sur l'équation du temps les p. 534 et suiv. du T. XV.

18) Comparez les p. 3-7 du T. XV.

19) Cette composition eût pu se faire de diverses façons. On peut consulter notre article ‘Deux pages consécutives du Manuscrit G de Chr. Huygens’ (T. XX, p. 594).

[p. 502]

mieux dire, le développement, l'évolution de la pensée intégrale de Huygens. Ici aussi nous devons toutefois nous contenter de l'à-peu-près. De l'à-beaucoup-près plutôt; dans les lettres de chaque époque il y a un fourmillement de noms et (tant dans elles que dans les manuscrits) de questions traitées dont on ne pourrait - plus ou moins! - tenir compte dans une biographie que si l'on se proposait de la rendre démesurément longue et absolument illisible. Il faut bien mettre en lumière ce qui semble être le principal et laisser le reste dans l'ombre. Pour le faire avec un discernement parfait, il faudrait d'ailleurs pouvoir se rappeler simultanément bien des choses.

Nous ne pourrions évidemment parler d'une évolution si l'étude de chaque sujet était due à des circonstances fortuites. Si Huygens n'avait pas entendu parler du problème des enjeux, peut-on dire, il ne se serait pas appliqué à ce calcul de probabilité et son livre de 1657 n'aurait pas vu le jour. C'est vrai, mais quand on parle d'évolution ce qu'il faut considérer c'est plutôt ce que l'homme se propose d'accomplir que ce qu'il accomplit réellement. Huygens - c'est cela qui importe - avait l'ambition de contribuer de son mieux à la résolution des grands problèmes - et même souvent aussi à celle de petits problèmes - antiques et modernes. Il devait donc tâcher de savoir quels étaient les problèmes considérés de son temps. Si Fermat et les autres mathématiens français s'étaient occupés du problème des enjeux sans en faire part à qui que ce fût en dehors d'un cercle intime, il semble bien qu'il ne serait pas de lui-même tombé sur ce sujet. L'essentiel, c'est qu'à l'époque considérée, qui est celle de son ascension, il était animé de la constans ac perpetua voluntas de voir aussi clair que possible, plus clair que tous s'il pouvait y réussir, dans les questions de mathématique pure, d'astronomie et de physique.

Pourquoi s'intéressait-il aux couronnes et parhélies ainsi qu'à l'arc-en-ciel? N'étaitce pas parce que Descartes avait écrit sur les Météores? Et que Gassendi s'y était intéressé encore avant lui? Voyez sur ce sujet notre Avertissement des p. 353 et suiv. du T. XVII²⁰⁾. Pourquoi voulait-il - et c'était là un sujet moins difficile, puisqu'il n'y fallait pas tant de conjectures - établir la théorie du choc des corps durs? C'est que, par ce moyen, en poursuivant les idées de Démocrite et d'Épicure, il espérait pouvoir rendre compte mieux que Descartes de plusieurs phénomènes physiques; voici le texte de la première page d'un manuscrit de 1656²¹⁾: ‘Si universa natura corpusculis quibusdam constat à quorum motu omnis rerum diversitas oriatur, quorumque celerrimo impulsu lux momento temporis propagetur et per immensa caeli spatia defluat, ut probabile esse multi philosophi existimarunt; non parum adjuvari haec contemplatio videbitur si verae motus leges innotuerint quaque ratione de cor-

20) Notamment la note 3 de la p. 354 et celles auxquelles cette note renvoie.

21) T. XVI. p. 150.

[p. 503]

poribus in corpora transferatur’. C'est là un véritable programme. Où, pourrionsnous ajouter, ne prédomine pas l'espoir que cette connaissance des lois de la nature pourra avoir des conséquences pratiques; c'est uniquement de mieux comprendre qu'il est ici question. Dans le cas des mathématiques pures il en est de même. Nous ne pensons pas que Huygens ou Pascal se soient jamais proposés de veiller à ce qu'un joueur acharné, forcé de quitter la partie, reçût précisément la somme qui lui était due. Mais c'était un plaisir d'y voir clair. C'était un plaisir aussi de comparer les solutions.

Généralement, il nous semble qu'à cette époque la science - quoique pouvant être utile soit directement, soit dans la suite, p.e. dans le cas des horloges destinées e.a. aux marins - était avant tout pour Huygens un jeu d'esprit; et aussi une affaire de famille; comparez les p. 448-451 qui précèdent.

Elle pouvait sans doute - dans le cas de la construction d'instruments - être utile en ce sens que les inventeurs pouvaient gagner de l'argent par des octrois. Quel inventeur y a jamais été absolument indifférent? Toutefois Huygens affirme, et ceci nous semble correspondre à tout ce que nous savons de lui, que ce n'était pas là son véritable but: ‘Il est vray (dit-il à propos de l'horloge à pendule) que j'ay estè longtemps sans songer à me preualoir de mon invention en cette maniere, et ne m'en ferois avisè sans la suggestion de quelques amis²²⁾’. Il pouvait vivre sans cela²³⁾ et par conséquent supporter avec calme les réclamations des horlogers de profession, sur lesquelles on peut consulter les p. 82-83 de notre T. XVII. Comme nous l'avons déjà dit en cet endroit, les discussions d'octobre 1658 avec ces horlogers ne furent pas infructueuses au point de vue scientifique: un an plus tard - voyez les p. 385 et suiv. du T. XVII tirées du Manuscrit A - Huygens aborda l'étude du pendule composé (sur lequel nous reviendrons plus loin). On apprend de ses amis, on apprend aussi de ses adversaires; et souvent les deux qualités se confondent.

Ce ne sont pas l'argent et les autres possessions matérielles seules qui constituent le capital de l'honnête homme. La science aussi est un capital. On en peut tirer gloire. À cet effet il convient de ne pas divulguer de suite les résultats obtenus ou les méthodes par lesquelles on y est parvenu. Huygens se sert volontiers, jusqu'à la fin de sa vie, - comme on l'avait fait déjà avant lui - d'anagrammes qui doivent assurer la priorité d'une découverte ou d'une formule jusqu'au moment où il semblera opportun de la faire connaître. Les publications hâtives lui répugnent; posséder la vérité est plus agréable que d'étaler ses connaissances; cette possession secrète - nous songeons aux lois de la percussion ainsi qu'à la formule, ou plutôt la loi, de la force centrifuge -

22) Lettre à Boulliau de juin 1658, T. II, p. 183.

23) Nous ignorons d'ailleurs si les octrois, ou du moins certains d'entre eux, lui ont rapporté des sommes considérables.

[p. 504]

donne un sentiment de supériorité. Comparez la note 2 de la p. 246 du T. XVII. On remarque la même chose p.e. chez Roberval²⁴⁾ et Newton.

En s'appliquant au perfectionnement des instruments propres à mieux nous faire connaître l'univers, Huygens a aussi le sentiment de servir l'État. La gloire des inventeurs est en même temps celle de la patrie. Voyez, aux p. 44 et suiv. du T. XVII, la Dédicace de l' ‘Horologium’ aux États de la Hollande et de la Westsrise où sont vantées les très célèbres inventions de l'imprimerie²⁵⁾ et du télescope auxquelles celle de l'horloge à pendule - encore dépourvue des arcs cycloïdaux, appelés ‘joues’ un peu plus haut - vient désormais se joindre: il convient aux ‘très illustres et très puissants membres’ des États de perpétuer le souvenir des inventions, de contribuer, en protégeant les inventeurs, à la gloire nationale. Nous rappelons qu'en 1658 dans le cas du télescope - et du microscope - l'attribution officielle de la priorité aux middelbourgeois - voyez la p. 471 qui précède - ne datait encore que de trois ans, que c'étaient en effet des illustres et puissants personnages qui s'étaient appliqués à acquérir définitivement cette gloire à la Zélande²⁶⁾. Huygens, parlant de plagiaires, émet incidemment un jugement défavorable sur son époque; ‘la candeur et l'ingénuité primitives’²⁷⁾ ont disparu et l'on ne pourrait guère espérer leur retour à moins que d'admettre dans les événements une certaine périodicité. Y a-t-il ici e.a. une réminiscence au temps des sages de Stevin²⁸⁾? Pour le moment, suivant lui, nous nous mouvons en sens inverse; dans la Dédicace du Système de Saturne à Leopoldo de Medicis il est question de ‘la barbarie grandissante de jour en jour²⁷⁾’. Conviction ou rhétorique? Comment concilier son idée d'une ‘barbarie grandissante’ avec sa foi à l'essor indéniable de la science, telle qu'elle se manifestait en lui-même et qu'il

24) T. I, p. 485.

25) Tout visiteur de la Hollande connaît la statue de Laurens Jansz. Koster qui se dresse sur la grand'place de Haarlem. Voyez sur lui la note 1 de la p. 48 du T. XVII.

26) Suivant le Journal de Beeckman, cité par C. de Waard, Zacharias Jansen de Middelburg lui aurait cependant dit que le premier télescope fut construit dans cette ville par son père d'après celui d'un italien. Il y avait une verrerie ou cristallerie semi-italienne à Middelburg. On n'a pu établir quel aurait été l'italien en question; de Waard a bientôt reconnu s'être trompé en émettant l'hypothèse de la probabilité de l'apport d'un télescope par un soldat italien: son opinion que le télescope, en ce temps, était connu à bien des militaires italiens, reposait sur une erreur de traduction (savoir celle de l'expression ‘per benefizio’ dans une lettre de Gualterotti à la p. 101 de ‘De uitvinding der verrekijkers etc.’). Quand un instrument passe des mains d'un constructeur capable à celles d'un autre, il en sort généralement amélioré, et finit par devenir un instrument pratique; le constructeur qui réussit à rendre l'instrument d'un usage général peut en un certain sens en être appelé l'inventeur. C'est ainsi qu'on a pu soutenir que Galilée et non pas Zacharias Jansen - ou Lipperhey - fut l'inventeur du télescope (‘Le questioni di priorità e dei precursori’ par A. Mieli, dans le No. 1 d'octobre 1947 des ‘Archives internationales d'Histoire des Sciences’).

27) Nous citons Huygens d'après notre traduction, T. XV, p. 216.

28) Voyez la p. 438 qui précède.

27) Nous citons Huygens d'après notre traduction, T. XV, p. 216.

[p. 505]

la constatait chez ses contemporains? C'est apparemment uniquement d'une barbarie morale qu'il parle, comme on le fait aussi au temps présent où le développement de la science et de la technique ne sont certes pas moins remarquables qu'au dix-septième siècle. Quant à la question du retour périodique, de l'alternative de l'ascension et du déclin, il conviendrait sans doute - ce que Huygens néglige ici; Aristote qu'il citera plus tard²⁹⁾ a aussi l'expression τὰς αὐτὰς δόξας ἀναϰυϰλεῖν ἐν τοῖς ἀνϑρώποις ἀπειράϰις - de ne pas parler de l'humanité en général, mais de considérer à part diverses civilisations, comme on le fait aujourd'hui.

Nous avons dit³⁰⁾ que Huygens - par opposition à son père - ne recherche point les expressions obscures ou le style fleuri. Mais les circonstances sont parfois plus fortes que l'homme. Aux p. 273-275 du présent Tome (se rapportant d'ailleurs à une Pière de beaucoup plus tard) il a dû être question d'une obscurité voulue. Quant au style fleuri - ce que Shakespeare appelle les ‘golden words’ du courtisan³¹⁾ - Huygens ne pouvait l'éviter entièrement dans les dédicaces aux princes. C'est à cette nécessité, bien plus qu'à une conviction sincère, que nous attribuons³²⁾ la glorification - dans l'esprit de Pythagore, et plus ou moins dans celui de Kepler - du nombre stellaire douze, de ‘la riche matière à contemplations qui se présentera aux esprits des philosophes à propos [de choses de ce genre]’. Il faut se rappeler que l'astrologie - ‘misérable folie³³⁾’ aux yeux de Huygens; ce n'est pas seulement vers la fin de sa vie qu'il le dit - était encore en vogue en bien des cours, même et surtout l' ‘astrologia divinatrix futurorum’³³⁾, non pas seulement celle dont il est ici question (sans qu'il soit fait usage du mot astrologie) qui se contente de spéculer sur les nombres dans le but de faire apparaître l'harmonie immanente de l'univers. Peut-on vraiment suivant Huygens parler d'une harmonie du monde? Dans les années 1656-1660, vers l'âge de trente ans, il ne semble pas s'être posé sérieusement des questions si générales et si vagues. Ce n'est que faute de mieux, pensons-nous, que, forcé d'adopter, pour pouvoir déterminer sans la mesurer la parallaxe du soleil (cette mesure lui semblait impossible; consultez dans le T. XXI la p. 308 ou la Table des Matières Traitées in voce ‘Parallaxe du soleil’), un rapport déterminé entre la grandeur de la terre et celle du soleil ou bien d'une planète, il prend dans le Système de Saturne pour celle de la terre une moyenne entre celles de Vénus et de Mars en se basant sur la plus ou moins grande concinnitas du système solaire.

Puisque ce n'est pas Huygens seul qui nous intéresse mais aussi son entourage, nous croyons bien faire d'observer, à propos de l'astrologie divinatrice, qu'en Hollande

29) T. XXI, p. 564.

30) p. 398.

31) Hamlet, Acte V, Scène Il.

32) Dans la Dédicace du Systema Saturnium à Leopoldo de Medicis, T. XV, p. 214-215.

33) T. XXI, p. 736.

33) T. XXI, p. 736.

[p. 506]

aussi, dans la famille du stadhouder Frédéric-Henri, et ailleurs, on paraît y avoir attaché quelque prix. Qu'un horoscope avait été dressé pour ce prince, cela résulte d'une lettre du 27 août 1644 de le Leu de Wilhem à son beau-frère Constantyn³⁴⁾: ‘Mandez moy, lorsque le capitaine des charpentiers eust la main rompue d'un coup de musquet tout joignant S.A. et de l'autre costé un sergent Anglois fut tué, s'il estoit necessaire que S.A. se tint là.....Ceux qui ont dressé son horoscope l'ont déclaré heureux en ses exploits et qu'entre ses mains tout reussiroit trop mieux que les apparences ne permettent d'attendre. Je n'espère pas que S.A. se hazarde sur telles predictions. Homines sunt et fallaces plerumque’. Cette dernière sentence semble indiquer que le Leu de Wilhem n'était pas bien convaincu, comme les Huygens, de la non-valeur absolue des horoscopes. Christiaan dit avoir eu grand-peine à faire croire à Albertina Agnes, une des filles de Frédéric-Henri, qu'il ne s'était jamais mêlé de dresser des horoscopes ni que même il n'y ajoutait aucune créance³⁵⁾.

Étant donnée cette mentalité des princes, la tournure pseudo-mystique d'une partie de la Dédicace du Systema Saturnium peut manifestement être considérée comme une captatio benevolentiae.

Les ‘travaux mathématiques divers de 1655 à 1659’ ont été publiés dans notre T. XIV³⁶⁾ avec un Avertissement³⁷⁾ qui donne bien des détails historiques. Cette compilation contient e.a. les recherches sur la cycloïde dues au concours institué par Pascal ainsi que la théorie des développées provenant de la forme des ‘joues’ du pendule. Consultez sur le centre de courbure la p. 211 qui précède.

Les dits travaux divers sont précédés dans le T. XIV par l'édition en néerlandais, avec traduction française, du Traité sur le Calcul dans les Jeux de Hasard³⁸⁾; et suivis par les ‘Contributions aux commentaires de van Schooten sur la Géométrie de Descartes’, éditions de 1649³⁹⁾ et de 1659; l'un et l'autre avec un Avertissement traitant tant du contenu que de la genèse.

Petite remarque: le mathématicien de Montmort (ou de Monmort) qui publia en

34) Worp ne donne qu'une partie de cette lettre. Le passage qui nous intéresse a été publié en 1676 dans les ‘Aanteekeningen en bijlagen’ à l'article de 1876 de D. Veegens ‘De Stichting der Oranjezaal’.

35) Lettres à Boulliau, qui lui s'en mêlait, de décembre 1659 et de janvier 1660 T. II. p. 523, T. III, p. 16 et 34.

36) P. 208-406 (quelques brèves pièces, datant de plus tard, y ont été intercalées en guise d'appendices).

37) P. 183-207.

38) Pourvu de nombreux appendices datant de plus tard.

39) Plus haut, en parlant des relations de Huygens avec van Schooten antérieures au voyage de 1655, nous n'avions pas encore attiré l'attention sur ces contributions.

[p. 507]

1708 un ‘Essay d'analyse sur les jeux de hasard’ n'est pas identique, comme l'admettent par inadvertance les Tables du T. XIV, avec le chef d'académie H.L.H. de Monmort, mentionné un peu plus haut⁴⁰⁾; ce n'était pas même un parent. Il s'appelait Pierre Rémond.

Laissons là le T. XIV - nous ajoutons seulement la remarque qui n'a pas été faite dans ce Tome, que dès 1657 nous voyons Huygens se servir de tables de logarithmes⁴¹⁾ - que tout lecteur peut lire ou feuilleter à sa guise et considérons de nouveau la correspondance de Huygens avec ses amis.

À Roberval Huygens put annoncer déjà le 18 avril 1656⁴²⁾ avoir ‘escrit les fondements du calcul es jeux de hasard à la prière de Monsieur Schooten qui le veut faire imprimer’.

Il y eut en effet, en 1656 comme auparavant, un grand échange de lettres entre Huygens et van Schooten. Ils y discutent amplement sur la question de savoir si Roberval a raison de dire⁴³⁾ - comme il l'avait déjà fait à Paris - qu'au début de la Géométrie de Descartes, là où il traite du théorème de Pappus, il y a une faute notable, critique que Huygens admet comme bien fondée⁴⁴⁾ mais contre laquelle van Schooten s'élève, ce qui donne lieu à Huygens de considérer de nouveau la question⁴⁵⁾ de telle manière que van Schooten peut écrire⁴⁶⁾: ‘quam planissimè et doctissimè, pro more tuo, difficultatem..explicas: ita ut nil putem Robervallo, praeter ejus libidinem in traducenda Cartesij mente, relictum iri’. La conclusion du professeur de Leiden, non pas celle de Huygens, était que Descartes avait été volontairement incomplet. Van Schooten annonce qu'il fera mention de la question ‘in commentarijs meis iteratè producturis’. Il le fit d'assez mauvaise grâce puisque dans cette deuxième édition de 1659 il ne nomme ni Roberval ni Huygens⁴⁷⁾. La troifième édition, celle de 1683 - soit dit en passant - fut identique à la deuxième: van Schooten ne vécut que jusqu'à 1660. On voit bien ici que Huygens est moins épris de Descartes que van Schooten⁴⁸⁾.

40) P. 499. Avec Huygens et bien d'autres nous écrivons dans le présent Tome: Montmor.

41) Voyez la p. 619 du T. XX. Mersenne avait attiré son attention sur les logarithmes en 1648 (p. 426 qui précède).

42) T.I. p. 404.

43) Dans sa lettre de juillet 1656, T.I. p. 449.

44) T.I. p. 464, 27 juillet 1656: ‘Ayant examinè vos remarques sur des Cartes je les trouve tresbelles et veritables etc.’

45) Lettre du 6 décembre 1656, T. I, p. 519.

46) Dans sa réponse du 12 décembre.

47) T. XIV, p. 414.

48) Sur l'histoire du problème de Pappus que Golius avait proposé à Mydorge avant de le proposer à Descartes, et que Mersenne, après avoir reçu la solution de ce dernier, proposa à Beaugrand et à Roberval, on peut consulter les notes des p. 261 et 294 du Vol. III de la Correspondance de Mersenne, publiée par M.^me P. Tannery, éditée et annotée par C. de Waard, Presses universitaires de France, Paris, 1946.

[p. 508]

Pour revenir aux calculs sur les jeux de hasard: ce ne fut pas seulement avec Roberval et Mylon que Huygens correspondit sur cette matière, ce fut aussi depuis mai 1656 avec de Carcavy qu'il avait vainement cherché à Paris mais qui fut amené par là à lui écrire en lui parlant tant de Fermat que de Pascal, du premier desquels Huygens put répondre connaître plusieurs écrits relatifs à d'autres sujets⁴⁹⁾. Quoiqu'il eût écrit avant mai 1656 ‘les fondemens du calcul es jeux de hasard’, il n'en resta pas là, grâce à cette correspondance.

Dans la même année (et déjà en 1655) il y eut aussi un échange de lettres entre Huygens et le mathématicien anglais Wallis qui auparavant correspondait déjà avec van Schooten. Il y est question de la célèbre formule de Wallis pour ce que nous appelons le nombre π⁵⁰⁾. Cette formule avait été obtenue, non pas par un raisonnement rigoureux, mais par une induction dont Huygens dit à plusieurs reprises ne pas être satisfait: ‘Multum tamen profecisse eum non opinor neque id admodum mihi placet, aut magnum geometram sapit, quod in demonstrando inductione utitur⁵¹⁾’. Huygens espérait toujours que la véritable quadrature du cercle, malgré l'infructuofité des efforts de ses contemporains, se montrerait un jour possible. Comparez les p. 308-309 et 370-374 du T. XX.

Cette correspondance fut continuée. C'est ainsi que Huygens, en 1659, signala à Wallis la méthode de Hudde pour trouver les maxima et minima des courbes algébriques⁵²⁾, non sans ajouter qu'il avait lui-même trouvé ce compendium avant Hudde et l'avait fait connaître à Joh. de Witt⁵³⁾; ce qu'on peut lire aussi dans le T. XIV⁵⁴⁾.

Nous avons vu que - sans partager l'animosité du professeur parisien - Huygens admettait avec Roberval que Descartes n'avait pas été ‘impeccable dans la Geometrie⁵⁵⁾’. Il ajoute qu'il n'avait pas non plus été impeccable dans la physique. C'est ce qu'il dit avoir fait voir dans son traité désormais achevé sur le choc des corps durs (ou plutôt sur le choc central de sphères dures). Nous ne voyons pas qu'il l'ait montré à van Schooten⁵⁶⁾ trop enclin à défendre Descartes et à le condamner, lui,

49) T. I, p. 428.

50) Comparez la note 3 de la p. 390 du T. XX où nous citons l'‘Arithmetica infinitorum’ de Wallis de 1655.

51) T.I. p. 441.

52) T. II, p. 417.

53) Comparez la note 4 de la p. 233 du T. XX, déjà citée à la p. 204 qui précède.

54) Note 1 de la p. 304.

55) T. I, 457, le 20 juillet 1656.

56) Le manuscrit, sur lequel on peut consulter la note 1 de la p. 137 du T. XVI, était - quoique Huygens dise son travail achevé - plein de ratures et d'apparence confuse. Le T. XVI n'en contient qu'un extrait publié comme Appendice à un texte mieux rédigé de la main d'un copiste, dont l'original perdu est d'une date inconnue postérieure à 1670 d'après la note citée. Le portefeuille ‘De Motu ex Percussione’ renferme de plus un assez grand nombre de feuilles séparées dont il a été fait usage dans le dit Tome.

[p. 509]

sans avoir vu ses arguments; en juillet 1656 van Schooten parle encore de ‘ista de quibus [en cas de publication] fama ac nominis tui apud eruditos celebritas, periclitari posset’.

Dans ce traité Huygens part e.a. de l'axiome suivant⁵⁷⁾ qui, d'après une remarque marginale dont nous n'avons pas tenu compte, aurait dû avoir été imprimé en grands caractères:

Certissimum in mechanicis est axioma, motu corporum qui a gravitate ipsorum proficiscitur, centrum commune gravitatis ipsorum non posse attolli.

On voit que, comme nous l'avons observé antérieurement⁵⁸⁾, il n'est pas question ici de la sphéricité de la terre ni de la cause qui rend les corps graves. La gravité de chaque corps est constante et il est parlé de l'élévation par rapport à un plan horizontal. L'axiome est évidemment emprunté à - ou suggéré par - l'expérience. Consultez aussi sur cet axiome la l. 9 de la p. 459 qui précède.

Ce n'est pas là le seul axiome, il en faut encore quelques autres que Huygens choisit de la façon qui lui paraît la plus convenable.

Les théorèmes sur la collision des corps, nous l'avons vu⁵⁹⁾, pourraient peut-être servir plus tard lorsqu'il s'agirait d'expliquer la propagation de la lumière; l'expression ‘celerrimus impulsus’ fait bien voir que dans l'esprit de Huygens cette propagation n'est pas instantanée comme l'admettaient tant Aristote que Descartes. Galilée, lui, ne l'avait pas jugée instantanée.

Pour pouvoir expliquer la nature des choses, il faut raisonner, mais surtout observer. La taille des lentilles demeure une des préoccupations constantes des deux frères aînés. Le 8 février 1656 Christiaan écrit, nous l'avons dit aussi à la 254 du T. XVII, qu'ils ont été occupés ces dix jours à donner la forme parfaite à une platine de fer reçue de Kalthof. En ce même mois - on le voit par une lettre à Mocchi⁶⁰⁾ - Christiaan dit songer sérieusement à entreprendre la taille de lentilles elliptiques ou hyperboliques; on peut voir dans le T. XVII⁶¹⁾ qu'il y songeait déjà en 1654; mais cet idéal de Descartes fut abandonné.

Christiaan dit avoir profité de ce qu'il avait appris chez Mocchi sur l'art de polir⁶⁰⁾.

57) Dans le manuscrit de 1656 il est formulé exactement comme dans le texte destiné à la publication, voyez les p. 57 et 146, note 4 du T. XVI.

58) P. 441.

59) P. 453 et 502.

60) T. I, p. 384.

61) P. 288-292.

60) T. I, p. 384.

[p. 510]

Le satellite de Saturne avait été découvert avec une lunette de 12 pieds. À la fin de juin 1656 Christiaan écrit⁶²⁾ en avoir construit déjà depuis quelque temps⁶³⁾ une de 24 pieds, avec laquelle il n'avait cependant, en juillet⁶⁴⁾, pas encore pu observer Saturne avec profit. L'oculaire était formé de deux lentilles planconvexes contigues⁶³⁾.

Voyez le dessin d'un trépied, datant de 1658, à la p. 181 qui précède⁶⁵⁾.

Une observation de 1657 de l'ombre de l'anneau de Saturne sur le globe a été mentionnée à la p. 40 du T. XV lequel contient aussi⁶⁶⁾ quelques observations des années ici considérées de Jupiter, de Vénus, de Mars, ainsi que d'autres observations de Saturne. Mais il y en a (sur Saturne) énormément plus dans le ‘Systema Saturnium’. L'Avertissement au Systema, qui parut en juillet 1659, en raconte clairement la genèse et donne une analyse du contenu, tandis que les p. 50-51 traitent de la méthode, ou plutôt des méthodes, de Huygens pour mesurer le diamètre des planètes; voyez aussi sur ces méthodes la Table des Matières du T. XXI in voce ‘Micromètres’. Il n'y put encore faire mention de son observation de 1659 suivant laquelle Mars tourne autour de son axe en environ 24 heures: cette observation date des derniers mois de l'année. D'ailleurs il ne voyait pas les taches assez distinctement pour se sentir sûr du résultat qui plus tard - avant qu'il eût rien publié lui-même - fut consirmé par d'autres astronomes. Voyez la p. 33 du T. XV.

Il est à remarquer que Huygens ne considéra pas seulement notre système planétaire. Il observa aussi les étoiles sixes, et put constater, contrairement à l'opinion de Riccioli et de beaucoup d'autres astronomes, que celles-ci n'avaient pas de diamètres mesurables⁶⁷⁾.

Observons encore que Huygens appelle le système planétaire de Copernic ‘divinitus inventum’⁶⁸⁾; et qu'il parle en pafsant d'habitants de Saturne (Saturnicolae), uniquement pour dire où se trouveraient pour eux les points équinoctiaux.

62) T. I, p. 441.

63) Comparez les p. 15-16 du T. XV, et la figure de la p. 162 du T. II.

64) T. I, p. 463. Lettre à Hevelius. Comparez la p. 197 du T. XV; les bras de la planète ne revinrent qu'en octobre.
Dans le Système de Saturne, au début, Huygens parle plus longuement de ses lunettes.

63) Comparez les p. 15-16 du T. XV, et la figure de la p. 162 du T. II.

65) Dont celui figuré à la p. 363 du T. II (année 1659) ne diffère pas beaucoup.

66) P. 55-69. Plusieurs autres observations avaient été consignées dans un ‘parvus libellus’ qui ne nous est pas parvenu.

67) T. XV, p. 190 et 233-237.

68) T. XV, p. 343.

[p. 511]

Il avait construit quelques années plus tôt deux ‘tabulas ligneas’ représentant les orbites planétaires; il en est fait mention en décembre 1657 pour la première fois. Nous avons dit à la p. 131 du T. XXI qu' à notre avis - car il ne donne aucune description des ‘tabulae’ - il s'inspirait du ‘Planeet-wijser’ de Rembrantsz. van Nierop, dont l'ouvrage astronomique a été mentionné à la p. 453 qui précède. Le ‘système de Copernic’ qu'il appelle ‘divinitus inventum’ n'est évidemment pas le système compliqué par de multiples excentriques qui avait paru nécessaire à Copernic pour sauver, à l'instar de Ptolémée, tous les phénomènes⁶⁹⁾; mais seulement le système simplifié qui consiste - d'après le premier livre de l'ouvrage de Copernic - à faire mouvoir toutes les planètes, y compris la terre, autour du soleil.

Dans les premières lignes du Systema Huygens ne manque pas d'affirmer que l'invention des télescopes a été faite dans nos Pays-Bas.

Son frère Constantyn ne se fait pas faute, non plus que l'ami Heinsius, de chanter la gloire de l'auteur. Il est presque superflu d'ajouter que si Constantyn appelle la planète maléfique (infaustum), ce n'est pas en astrologue qu'il parle, mais simplement en poète qui dans ses vers se conforme à la tradition.

Bientôt après Huygens mentionne Chapelain et Gassendi, plus loin aussi Roberval qui avait fait une autre hypothèse sur la cause de la variabilité de la forme de la planète.

Huygens eût pu faire paraître son ouvrage sur Saturne et son anneau déjà en 1656⁷⁰⁾; il l'aurait fait s'il n'avait pas en somme préféré attendre jusqu'à ce que son hypothèse, sur laquelle il gardait scrupuleusement le secret, aurait été mieux confirmée par l'observation. En attendant, il s'occupa de l'amélioration des horloges; vers la fin de 1656⁷¹⁾ il conçut la fourchette, rendant possible la régularisation de la marche par un pendule librement suspendu. Ce pendule détrôna peu à peu, et même assez rapidement, l'ancien balancier. L'invention était en l'air (comme on peut s'en convaincre en lisant les notes que nous avons ajoutées au premier Avertissement du T. XVII) tout comme celle du télescope l'avait été vers 1600. ‘Each [scientific victory] was won by a series of efforts the humblest of which was deliberate to a degree’; cependant ‘the men who clinched the great discoveries, who made or seemed to make the gigantic steps upward, were most of them outstanding personalities in their own

69) Voyez, dans une lettre de Huygens l'expression ‘sauver les phénomènes’ (σώζειν τὰ ϕαινόμενα), T. V, p. 29, où cependant le mot ‘sauuer’ a été mal lu.

70) T. XV, p. 182-183.

71) T. XVII, p. 3, début de l'Avertissement.

[p. 512]

right; not simply conspicuous or lucky men⁷²⁾’. Dans ces premières horloges l'amplitude des oscillations était grande et quelque peu inconstante; il convenait donc de rendre les oscillations isochrones par des ‘joues’ ou platines courbes dont la forme ne pouvait être déterminée que par des expériences prolongées. Bientôt Huygens cessa de les appliquer, ayant modifié le mécanisme des rouages de manière à rendre toutes les oscillations petites.

Les horloges à pendule furent mentionnées dans le Systema Saturnium. Il y fut aussi question - en un seul et bref passage - sans que Descartes fût nommé, de l'hypothèse ou croyance que Saturne, aussi bien que la terre, ‘est situé au milieu de son tourbillon et que tout ce qui là-bas est estimé avoir du poids [deuxième allusion à l'existence possible de planéticoles] tend par sa nature vers le centre de ce tourbillon⁷³⁾’.

Il nous semble, d'après ce passage, que Huygens en 1659 ne songeait pas encore à des tourbillons multilatéraux: comparez la p. 438 du T. XXI, où nous laissons indécise l'époque à laquelle il crut devoir rectifier la théorie de Descartes en ce sens. En 1659 il pouvait admettre (comparez la note de la dite page) que le vortex qui mène un anneau ou une lune est le même que celui qui cause la pesanteur auprès de la surface de la planète considérée; ce qu' évidemment il ne crut plus quelques années plus tard - voyez les p. 561 et 585 du T. XIX - lorsqu'il eut inventé les tourbillons multilatéraux pour la gravitation terrestre sans les étendre jusqu'à la lune qui continuait à être menée par un vortex unilatéral, jusqu'au jour où l'extension à la lune, par Newton, de la gravité terrestre, l'amena à admettre pour elle aussi les tourbillons multilatéraux⁷⁴⁾. De cette façon l'identité d'explication par voie tourbillonnaire du cours de la lune (ou d'une lune quelconque ou d'un anneau) et de la chute des corps pesants⁷⁵⁾ fut rétablie⁷⁶⁾.

Revenons à l'année 1659. De cette année - celle de la publication du Systema - date apparemment la feuille séparée - inédite jusqu'à 1932 - que nous avons publiée aux p. 276-277 du T. XVII. Huygens y énonce le principe que la gravité d'un

72) G. Sarton ‘The history of science and the new humanism’ (p. 22-23), Cambridge, Mass. Harvard Univ. Press, 1937.

73) T. XV, p. 300.

74) T. XXI, p. 439.

75) Voyez, outre la dite p. 439, la note 45 de la p. 438 du T. XXI.

76) Après avoir écrit ces pages, mais avant l'impression, nous reçumes de la part de Mons. A.E. Bell son livre ‘Christian Huygens and the development of science in the seventeenth century’ (London, E. Arnold & Co. 1947) où l'auteur remarque à bon droit (p. 33): ‘To this day noone seems to have recognized the importance of Huygens's theory...He did not state that the gravitational force kept the ring in rotational stability but he did suggest that Saturn's gravity extended to the ring’.
Voyez sur la rotation de l'anneau de Saturne la lettre de Chapelain du 4 mars 1660 et la réponse de Huygens du 28 avril (T. III).

[p. 513]

corps est équivalente au ‘conatus a centro recedendi’ d'une quantité égale de matière; ce qui permet de calculer la vitesse de la matière tourbillonnante. C'est ce principe - nous l'avons expliqué dans les notes 8 de la p. 277 du T. XVII et 8 de la p. 303 du T. XVI - qui lui fait connaître la grandeur absolue de la force centrifuge, d'abord pour la dite matière circulant autour de la terre et causant la gravité des corps visibles, ensuite aussi pour des mouvements circulaires quelconques. Déjà dans la dite feuille il se figure apparemment une particule circulant autour de la terre avec une vitesse telle que la force centrifuge qu'elle éprouve est précisément égale à la force qui tend à la faire descendre. Cette particule, pourrions-nous dire maintenant, est un satellite fictif, une petite lune, de la terre.

En ce temps il ne connaissait pas encore le passage de Plutarque sur la lune (p. 155 qui précède, et p. 553-554 du T. XXI).

Cette détermination de la valeur absolue de la force centrifuge est un des grands mérites de Huygens, dont personne, que nous sachions, ne lui a jamais contesté la priorité.

Il comprit aussitôt qu'il n'est pas nécessaire de commencer par la considération de la matière céleste hypothétique et composa un traité sur la force centrifuge où la matière tourbillonnante à laquelle seule il avait pensé d'abord n'est plus mentionnée du tout. Galilée (qui n'a pas la prétention d'expliquer la nature de la gravité) avait considéré, de même que Descartes, le mouvement de rotation; nous en avons parlé au T. XVI dans notre Avertissement au dit traité ‘De Vi Centrifuga’. Certaines figures de Huygens ressemblent beaucoup à celles du savant italien. Huygens calcula en premier lieu de combien la force centrifuge due à la rotation du globe terrestre fait diminuer la gravité à l'équateur, savoir de 1/265⁷⁷⁾. Voyez la p. 245 du T. XVII pour la valeur adoptée par lui, d'abord d'après autrui, ensuite d'après ses propres expériences, en et peu après ce mois d'octobre 1659, pour la distance parcourue en une seconde pour un corps tombant librement en partant du repos, en d'autres termes pour l'accélération de la pesanteur. L'expression ‘acceleratus motus’ se trouve e.a. à la p. 277 du T. XVII. On verra dans le dit T. XVII un chiffre résultant d'une expérience de novembre 1659 avec un pendule conique, ainsi qu'une détermination tout aussi bonne de décembre à l'aide de la règle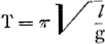



qui donne le temps d'une oscillation d'un pendule simple de longueur l⁷⁸⁾. Huygens venait de trouver cette règle; sans, il est vrai, l'exprimer en cette brève formule

77) T. XVI, p. 304.

78) g étant l'accelération de la pesanteur.

[p. 514]

qu'aujourd'hui tout-le-monde connaît. Il aurait alors pu corriger la fraction 1/265 en 1/302⁷⁹⁾.

La considération de la force centrifuge conduisit en effet naturellement à celle du pendule conique, et celle-ci à la construction d'une horloge à pendule conique.

Toutefois, comme la description de cette horloge est datée 5 octobre 1659⁸⁰⁾, tandis que les premières pages⁸¹⁾ (rédaction provisoire) du traité sur la force centrifuge portent la date du 21 octobre, il est également possible que l'horloge ait été inventée d'abord. Plus tard Huygens dira - mais samémoire était-elle bonne? - l'avoir inventée déjà en 1658⁸²⁾. Quoi qu'il en soit, les deux sujets sont étroitement liés.

La force centrifuge - voyez ce qui a été dit sur la feuille séparée de 1659 - est pour Huygens une force tout aussi réelle que celle de la gravité⁸³⁾. De même, dans les rotations d'un pendule ou d'une fronde, la force centrifuge est aussi réelle que la tension du fil ou de la corde. Il serait bien superflu de le dire, n'était la circonstance que dans la mécanique classique telle qu'elle s'est développée au dix-huitième siècle et plus tard, la force centrifuge a été considérée (nous pourrions dire: a dû être considérée) comme une force fictive par opposition à la force réelle de la gravitation⁸⁴⁾. La conception de Huygens nous paraît cependant plus naturelle. Prenons p.e. la Prop. XVI du Traité: ‘Lorsqu'un pendule simple est animé de la plus grande oscillation possible, c'est à dire lorsqu'il descend suivant un quart de circonférence, il tendra son fil, lorsqu'il aura atteint le point le plus bas de la circonférence, avec une force égale à trois fois celle qu'il exercerait s'il y était simplement suspendu’. Peut-on raisonnablement dire que de cette force la tierce partie est réelle, tandis que les deux autres tiers ne le sont pas?

Dans le traité de la percussion des corps durs, nous l'avons dit plus haut⁸⁵⁾, Huygens prenait pour une de ses hypothèses le principe de la relativité pour les mouvements uniformes, autrement dit il supposait qu'un mouvement uniforme quelconque donné à tout un système de corps n'y modifie en aucune façon les phénomènes. Dans le Traité de la force centrifuge il se sert aussi d'un principe de relativité pour les mouvements accélérés⁸⁶⁾: un petit corps qui se détache du bord d'une roue tournant

79) T. XVI, p. 326 note 4. Plus tard, ayant appris à mieux connaître la grandeur de la terre, il trouva 1/289 (même note).

80) T. XVII, p. 88. Le texte est emprunté au Manuscrit A.

81) Feuilles séparées.

82) T. VII, p. 391 et T. XVII, p. 242, note 7.

83) Voyez p.e. à la p. 266 du T. XVI la sentence: ‘cette tendance [centrifuge] dont nous avons parlé est absolument semblable à celle avec laquelle les corps pondérables suspendus à un fil aspirent à descendre’. Comparez la note 87.

84) T. XVI, p. 247, note 4.

85) P. 459.

86) T. XVI, p. 249; T. XVIII, p. 659.

[p. 515]

uniformément - la pesanteur étant exclue - possède un mouvement uniforme par rapport au milieu dans lequel la roue tourne, et un mouvement accéléré par rapport à un observateur attaché à la roue; la tendance à prendre ce mouvement accéléré relatif fait que le petit corps exerce sur la main de l'observateur nommé qui le retient une force réelle⁸⁷⁾.

La règle équivalente à la formule 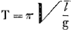dont il était question plus haut⁸⁸⁾ ne s'applique - quoique la formule soit approximativement vraie pour un pendule mathématique ordinaire - qu'au pendule mathématique cycloïdal⁸⁹⁾.

Ce fut en effet vers le premier décembre 1659 que Huygens avait fait l'ingénieuse découverte de ce pendule; découverte dont traitent les p. 344-349 d'un Avertissement du T. XVI.

Les horloges dont les pendules ne faisaient que de petites oscillations (modèle de 1658), portées en mer, se seraient arrêtées bien souvent; il pouvait donc sembler important de rendre les oscillations de nouveau larges ce à quoi la détermination exacte de la forme des ‘joues’ empiriques de 1657 - si intéressante d'ailleurs en ellemême - lui avait paru nécessaire⁹⁰⁾.

Huygens avait découvert auparavant, sans doute en octobre⁹¹⁾, la condition de l'isochronisme⁹²⁾ du pendule mathématique⁹³⁾ conique, quoique sans en déduire une construction: il savait désormais qu'il s'agit de maintenir le mobile, en cas de variation de l'amplitude des circonférences de cercle décrites, sur un certain paraboloïde⁹⁴⁾ de révolution.

Dès lors il avait cherché avec ardeur, et bientôt avec succès, la vraie forme des ‘joues’ convenant au pendule mathématique ordinaire. Ses lettres à Boulliau et van Schooten⁹⁵⁾ font voir que, de toutes ses inventions, celle-ci lui sembla la plus belle.

87) Aussi réelle du moins que toute autre force. On peut consulter le dernier alinéa de la p. 16 qui précède. - Mais le lecteur fera sans doute bien de ne tenir aucun compte de ce passage où il est fait allusion à des théories de pressions et de mouvements de matières subtiles auxquelles Huygens, en écrivant son traité sur la force centrifuge, ne songeait pas - comparez la p. 9 du T. XIX - tout aussi peu que lorsqu'il écrivait son ‘De iis quae liquido supernatant’ (voyez le deuxième alinéa de la p. 441).

88) Voyez cette règle à la p. 410 du T. XVI, dernier alinéa.

89) Nous appelons toujours pendule mathématique un pendule consistant en un fil impondérable portant à son extrémité inférieure un seul point pesant.

90) T. XVII, p. 93.

91) T. XVII, p. 95, note 1, renvoyant à la p. 87.

92) Ou ‘tautochronisme’ (Avertissement mentionné du T. XVI).

93) Pendule mathématique, autrement dit: pendule simple.

94) Appelé en ce temps conoïde.

95) T. XVI, p. 344-345.

[p. 516]

Elle lui parut digne d'un traitement mathématique convenable. La ‘demonstratio melior huc tandem redacta’⁹⁶⁾ est du 15 décembre. Tant Galilée qu'Archimède y sont cités en marge. Suivant son habitude, il ne montra aucune envie d'exposer immédiatement aux regards de tous ce qu'il avait trouvé. Dans les lettres citées à van Schooten et Boulliau il ne dit pas quelle est la forme calculée des platines courbes ni quelle est la courbe décrite par le mobile. C'est ce qu'il réserve pour une deuxième édition de l' ‘Horologium’ qui eût pu paraître déjà en 1660⁹⁷⁾. Il n'avait pas en ce moment l'intention d'y donner à sa démonstration la forme rigoureuse ‘more veterum’ qui aurait nécessité ‘longum ambitum’⁹⁸⁾. Voyez le Sommaire de 1660 à la p. 120 du T. XVII.

Au sujet des théorèmes et des démonstrations du traité sur la force centrifuge nous croyons encore devoir mentionner que dans un paragraphe qui n'a pas été incorporé au traité⁹⁹⁾ Huygens avait fait d'abord usage de formules algébriques¹⁰⁰⁾. Dans le dit paragraphe Huygens n'indique par des lettres que des lignes; il ne se sert pas de lettres pour désigner des quantités de matière ou des poids, des vitesses ou des accélérations¹⁰¹⁾. Ailleurs, en cette même année 1659, il désigne aussi parfois la ‘gravitas’ d'un corps donné par une lettre¹⁰²⁾. Le mot ‘gravitas’ n'a d'ailleurs pas toujours le même sens¹⁰²⁾; nous l'avons remarqué aussi dans l'Avertissement au Traité de la force centrifuge¹⁰³⁾. Il est e.a. question pour les corps tombants ou suspendus du ‘conatus qui est ex gravitate’¹⁰⁴⁾; ce ‘conatus’ c'est ce que les grecs appelaient ῥοπ.

La considération du fil s'adaptant à la courbe cycloïdale conduisit naturellement à celle des développées et développantes en général. Dans le T. XIV les Pièces de 1659 qui s'y rapportent occupent les p. 387-405.

En cette même année 1659 Huygens semble avoir eu en vue encore une autre publication¹⁰⁵⁾. Il s'était occupé de nouveau de la quadrature des surfaces des sphé-

96) T. XVI, p. 405.

97) T. XVII, p. 117.

98) T. XVI, p. 412.

99) Le § 15 de la p. 309 du T. XVI.

100) Il se sert également de formules algébriques dans un calcul du même mois de décembre 1659 où il fait un premier effort pour calculer la période d'un pendule simple dépourvu d'arcs cycloïdaux et exécutant des oscillations de 180^o (T. XVIII, p. 374).

101) Comparez sur ce sujet la p. 459 qui précède.

102) Voyez, à la p. 384 du T. XVI, la Pièce sur la chute de sphères dans des milieux résistants. Comme nous l'avons remarqué en cet endroit, le mot ‘gravitas’ y désigne tantôt le poids spécifique, tantôt le poids lui-même.

102) Voyez, à la p. 384 du T. XVI, la Pièce sur la chute de sphères dans des milieux résistants. Comme nous l'avons remarqué en cet endroit, le mot ‘gravitas’ y désigne tantôt le poids spécifique, tantôt le poids lui-même.

103) T. XVI, p. 245.

104) T. XVI, p. 267.

105) T. XIV, p. 336.

[p. 517]

roïdes et des conoïdes hyperboliques et avait apparemment l'intention de rédiger en entier un traité qui devait contenir, avec la rectification de la parabole, ses découvertes sur ces quadratures et peut-être encore d'autres inventions géométriques, p.e. la quadrature des courbes paraboloïdes et hyperboloïdes¹⁰⁶⁾. Des parties en avaient déjà été bien rédigées. Nous avons parlé du compromis auquel il se décida¹⁰⁷⁾, savoir à se servir quelquefois des indivisibles, donc à ne pas donner partout une démonstration rigoureufe, mais seulement ‘le fondement d'une telle démonstration’. Cette publication n'eut pas lieu.

Parmi les courbes envisagées par Huygens, nous voulons encore mentionner ici - quoiqu'en général, comme nous l'avons dit, nous croyions pouvoir renvoyer au T. XIV - outre la cycloïde, dont nous avions déjà dit un mot à propos du concours institué par Pascal en juin 1658¹⁰⁸⁾, les perles de de Sluse et la cissoïde. Le dit concours donna lieu à une brève correspondance avec Pascal qui fit e.a. connaître à Huygens la rectification de la cycloïde, et de tout arc de cycloïde, par Wren; que Huygens put obtenir à son tour. Quant à l'abbé belge bien connu de Sluse, Huygens avait été mis en rapport avec lui par son père en 1657¹⁰⁹⁾; depuis ce temps les lettres échangées furent nombreuses. Déjà dans la première lettre il est question du problème déliaque (duplication du cube) et bientôt¹¹⁰⁾ Huygens propose celui d'Alhazen. En mars 1658 Slusius mentionne la cissoïde¹¹¹⁾ ce qui donne lieu à un échange de vues sur sa quadrature¹¹²⁾ ainsi que sur la cubature des solides de révolution qui lui correspondent. Van Schooten, Hudde, Fermat, van Heuraet¹¹³⁾, Wallis et Mylon participent parfois aux discussions. Voyez notamment la longue lettre du 1 janvier 1659 de Wallis à Huygens qui fut imprimée en cette année (Posterior tractatus in quo agitur de Cissoide, et Corporibus inde genitis: et de Curvarum, tum Linearum εὐϑύνσει tum supersicierum πλατυσμῷ) avec le Tractatus Prior, de Cycloide etc. La grande question c'est toujours la quadrature du cercle: d'autres quadratures - voire même des cubatures - peuvent être considérées comme des ἀπαγωγαί¹¹⁴⁾. Huygens avait fait connaître à beaucoup de ses correspondants son théorème de 1657 sur la

106) Autrement dit: les paraboles et hyperboles de divers degrés.

107) T. XIV, p. 190-191.

108) Voyez aussi sur ce sujet la p. 187 du T. II.

109) T. II, p. 36.

110) T. II, p. 45.

111) T. II, p. 144.

112) Voyez e.a. les p. 309-312 du T. XIV.

113) Son article de 1659 ‘De transmutatione curvarum linearum in rectas’ est mentionné à la p. 189 du T. XIV.

114) Comparez les p. 199-200 du T. XIV.

[p. 518]

rectification de la parabole, c.à.d. sur la réduction de ce problème à celui de la quadrature du cercle¹¹⁵⁾.

Christiaan s'intéressait-il aussi en ce temps aux larmes de verre? On pourrait le croire d'après la lettre du 30 mars 1657 de lady Newcastle sur ce sujet. Dans le T. II nous avons dit supposer que cette lettre était adressée à lui plutôt qu'à son père. Nous ignorions, ce que l'édition de la Correspondance par Worp a révélé, que le père Constantyn avait entamé ce sujet dans deux lettres à la duchesse¹¹⁶⁾ du même mois¹¹⁷⁾: c'est à lui que la réponse¹¹⁸⁾ s'adresse. Citons une partie de ses lettres¹¹⁹⁾: ‘these wonderfull glasses, which, as I told you, Madam, will fly into powder, if one breaks but the least top of their tailes, whereas without that way they are hardly to be broken by any waight or strength. The King of France is as yet unresolved in the question, notwithstanding he hath beene curious to moove it to an assemblie of the best philosophers of Paris, the microcosme os his kingdome.....Experience having carried me to a new byway, from whence I do not see how to bring myselfe upon the path of truth without your gracious assistance, I doe presume this second time to informe your Ex.^cie of what I have found out....In ordre of your Ex.^cies determination, I did conceave, if the matter inclosed in the hollow parts of these bottels should be a sulphureous liquid gunpowder, that without question fire would work upon it, and make it active. But, Madam, I found myself so farre short of my opinion, that firing one of these bottels to the reddest hight of heat, I have not onely seene it without any effect, but also being cooled again, I have wondred to see all hís vertue spent and spoiled, so that I could breake of the whole taile by peeces even to the belly, without any motion more then you would see in an ordinarie peece of glasse....’

Sans doute à la maison du Plein ce phénomène a été un des nombreux sujets de conversation entre le père et ses fils. Mais, comme nous l'avons dit antérieurement en parlant du bois pourrissant spontanément lumineux - le livre de Kircher, cité à la p. 522 qui suit, traite longuement des corps luisants - Christiaan avait le bon sens de ne pas s'aventurer dans des explications de phénomènes trop compliqués. Tout en

115) T. XIV, p. 189 et 195.

116) Née Margaret Lucas, épouse de William Cavendish, duc de Newcastle (1592-1672). Ils étaient domiciliés à Anvers.

117) Ou plutôt: il continue par écrit la conversation qu'il avait eue avec elle sur ce sujet.

118) Non seulement celle du 30 mars, mais aussi une première et plus longue réponse du 20 mars, qui se trouve également chez Worp.

119) Chez Worp elle porte le no. 5535.

[p. 519]

ayant osé soutenir assez hardiment en 1656¹²⁰⁾ - mais en ce moment il ne songeait pas, nous semble-t-il, au problème de la cohésion - que ‘omnis rerum diversitas’ provient du mouvement de certains corpuscules.

Une lettre du 14 octobre 1658 du père Constantyn au ‘Roi d'Angleterre’ Charles II - qui, il est vrai, résidait en Hollande en ce temps et ne devint officiellement roi qu'en 1660¹²¹⁾ - résumée par Worp, nous apprend que Christiaan, évidemment sur l'initiative du père, lui offrait un télescope; le maniement était expliqué dans la lettre; c'est apparemment de ce télescope-là que Christiaan parle en 1662¹²²⁾. En 1661 le père - qui, on l'a déjà vu, vante et pousse toujours son fils - écrira que le roi honore Christiaan ‘d'une estime fort particuliere’¹²³⁾. Voyez encore sur ce sujet les l. 7-8 de la p. 277 de notre T. III, et le n^o III de la p. 172 qui précède.

Huygens garda le secret sur l'anneau de Saturne jusqu'au 28 mars 1658; voyez sa lettre à Chapelain de cette date. Il y eut cependant une exception: Boulliau vint le visiter à la Haye où il fut en 1657 durant quelques mois le secrétaire de l'ambassadeur de Thou. Or, sa lettre de janvier 1658¹²⁴⁾ montre que Huygens lui avait fait voir l'anneau; cependant, ajoute-t-il, ‘je vous donne ma foy et ma parole que personne ne verra & n'aura communication de ce que vous m'avez fait l'honneur de me communiquer avec tant de bonté et de courtoisie’.

Ce n'est pas que Boulliau est entièrement convaincu que ce qu'il a vu est réellement un anneau; même après avoir lu en novembre 1659 le Systema Saturnium il dit s'en tenir encore au doute¹²⁵⁾.

Déjà avant l'arrivée de Boulliau à la Haye Huygens dit se réjouir de l'occasion qu'il aura de causer avec lui sur ‘quelques opinions particulieres’ avancées par lui dans son ‘Astronomia philolaica’, notamment sur l'équation des jours¹²⁶⁾, sujet con-

120) P. 502 qui précède.

121) Oliver Cromwell était mort en septembre 1658. Après lui, son fils Richard eut pour quelque temps le titre de Protector.

122) T. IV, p. 92; T. XV, p. 16, où l'on voit les noms d'autres personnes qui reçurent des télescopes, e.a. Boulliau. On peut y ajouter le nom Colvius (T. I, p. 470).

123) T. III, p. 255.

124) T. II, p. 117.

125) T. II, p. 511.

126) T. II, p. 7.

[p. 520]

troversé¹²⁷⁾. Nous avons dit plus haut qu'en 1658 Huygens en traite dans le Manuscrit A; il se proposait d'en traiter dans l'édition amplifiée de l' ‘Horologium’; au début de 1657 Mylon¹²⁷⁾ parle déjà de ‘vostre invention nouuelle pour l'Equation du temps’. Depuis que Boulliau fut rentré à Paris jusqu'en 1660 les lettres échangées furent nombreuses. En décembre 1657 Huygens le ‘supplie de ne communiquer à personne ce que vous scavez du monde Saturnien’. Il lui apprend que bientôt l'horloge d'un clocher de village - il s'agit de Scheveningen près de la Haye - sera pourvu d'un long pendule. Voyez sur ce sujet ainsi que sur d'autres horloges publiques auxquelles des pendules furent adaptés, les p. 32 et suiv. du T. XVII. Les horloges fournirent le sujet de bien d'autres lettres encore. Huygens envoya des horloges à Boulliau ainsi qu'à d'autres parisiens. Nous apprenons que des objections furent faites à la construction. C'est ainsi que Huygens écrit¹²⁸⁾: ‘Si vous estiez de l'académie chez Monsieur de Monmor je vous prierois d'y faire veoir [mes] raisons, parce que Monsieur Chapelain mande qu'encore dernierement on y a fait de semblables objections à la vostre’. Boulliau fut aussi en correspondance avec le prince Leopoldo de Medicis - nous avons mentionné à la p. 495 le telescope qu'il avait reçu auparavant de son frère, le grand-duc Ferdinando - qui lui envoya des figures, lesquelles il transmit à Huygens, de l' ‘Horologe commencé par Galileo Galilei avec un pendule’ et de ‘l'horologe a pendule qui est a Florence dans le vieil palais de Medici’. On peut les voir dans notre T. III vis-à-vis des p. 8 et 14. Nous nous sommes étendus sur les constructions de Florence dans un Avertissement du T. XVIII¹²⁹⁾.

Boulliau reçut aussi de Huygens des lentilles¹³⁰⁾ et une lettre avec des figures sur le grand télescope à construire¹³¹⁾.

Ce fut à Boulliau que Huygens envoya en août 1659 un certain nombre d'exemplaire du Systema Saturnium pour en faire la distribution¹³²⁾.

Parlant de l'observation d'éclipses - et autres observations; il est question du ‘changement en l'estoile du Cigne¹³³⁾’ - Huygens blâme l'Université de Leiden

127) Voyez, à la p. 9 du T. II, ce que Mylon dit sur ce sujet en citant Frenicle. En mai 1659 Huygens écrira encore à Boulliau que sa méthode lui est ‘un peu suspecte’, en février 1660: ‘Je desespere de vuider cette question par lettres’.
Voyez cependant sa longue lettre de 1662 sur ce sujet à P. Petit (T. IV, p. 138-142).
On peut consulter dans le T. XXI (p. 316-318) ce que Huygens écrira encore en 1680 sur l'équation du temps; il approuve toujours la méthode de Ptolémée et de Copernic et désapprouve celle suivie e.a. par Boulliau, quoiqu'on puisse aussi parler d'un ‘error Ptolemaei et Copernici’ (T. XV, p. 547, T. XVII, p. 123).

127) Voyez, à la p. 9 du T. II, ce que Mylon dit sur ce sujet en citant Frenicle. En mai 1659 Huygens écrira encore à Boulliau que sa méthode lui est ‘un peu suspecte’, en février 1660: ‘Je desespere de vuider cette question par lettres’.
Voyez cependant sa longue lettre de 1662 sur ce sujet à P. Petit (T. IV, p. 138-142).
On peut consulter dans le T. XXI (p. 316-318) ce que Huygens écrira encore en 1680 sur l'équation du temps; il approuve toujours la méthode de Ptolémée et de Copernic et désapprouve celle suivie e.a. par Boulliau, quoiqu'on puisse aussi parler d'un ‘error Ptolemaei et Copernici’ (T. XV, p. 547, T. XVII, p. 123).

128) T. II, p. 442.

129) P. 59-66 du dit Tome.

130) Par l'entremise de l'abbé Brunetti, connaissance intime de Slusius (T. III, p. 71 et 361).

131) Mars 1659, T. III, p. 361.

132) T. III, p. 453 et 488.

133) Voyez sur cette étoile la note 10 de la p. 225 du T. III.

[p. 521]

de ne pas suffisamment y prendre part: ‘Pour les Messieurs de Leyden je ne scay s'ils y prennent garde. C'est une honte qu'il n'y a personne là qui face des observations ny d'eclipse ny de quoy que ce soit, sinon un seul Allemand nommé Kechelius¹³⁴⁾’. Kechel a été plusieurs fois mentionné dans notre T. XVII à propos des couronnes et parhélies; on y voit, quoi qu'en dise Huygens, que Golius observait parfois avec lui¹³⁵⁾. Dans ce même Tome, dans notre Avertissement au Traité ‘de Coronis et Parheliis’, nous avons dit qu'il ressort de la Correspondance qu'en septembre 1659 Huygens demanda avec un certain succès à Chapelain de lui procurer par l'intermédiaire de de Montmor la description du ‘deuxième phénomène de Rome’ de 1630, qui devait se trouver dans les papiers de feu Gassendi. En 1660 il affirme que son traité est fort avancé. Notons qu'en 1659 il avait observé lui-même plusieurs halos et aussi des parhélies¹³⁶⁾.

Boulliau voit tout aussi bien que Huygens que l'observation d'une seule étoile variable peut être considérée comme suffisante pour infirmer l'opinion d'Aristote ‘de l'incorruptibilité & ingénérabilité des cieux¹³⁷⁾’.

Ce qui a été écrit ici sur la période considérée suffira, croyons-nous, à ceux qui ne voudront pas prendre la peine de lire d'autres lettres que celles citées par nous, pour se faire une idée des oeuvres de Huygens et de la correspondance de ces années.

Reste toutefois de dire un mot sur la lanterne magique de 1659 ou de plus tôt (p. 197 qui précède), ainsi que sur la polémique avec Eustachio Divini de 1660.

134) T. III, p. 509.

135) Et ce fut Golius qui attira l'attention de Boulliau sur l'étoile variable du Cygne (T. III, p. 227).

136) T. XVII, p. 472. Appendice VII au Traité des Couronnes et Parhélies.

137) T. II, p. 228.
Pendant l'impression du présent Tome on nous envoie de l'Observatoire de Paris (collection-Boulliau) le résumé suivant de la lettre de Huygens du 9 janvier 1659 quin ous manque (d'après la p. 318 de notre T. II):
A la Haye. 9 Janvier 1659.
Remarq. Almagest. Ricciol. part. 1^er pag. 712. col 1. in fine. que Saturne du 2 Janvier 1650 au 3^e. etoit devenu australior quoniam retrogradus incedebat per orbitam suam. il est vray que australior evasisset s'il eut marche en retrograd. dans son orbite. mais il devoit sçavoir que le chemin apparent des planetes ne demeure pas dans un seul cercle qui soit leur orbita. Remarq. encore ib. p. 723. Schol. 2.

[p. 522]

En 1694 Huygens trace la figure d'une lanterne magique à deux lentilles¹³⁸⁾. On y lit: laterna magica. speculum cavum. lucerna. lens vitrea. pictur a pellucida [nous soulignons]. lens altera. paries.

En 1659 il s'en servait probablement pour amuser des jeunes gens, des membres de la famille. Il construisit e.a. une lanterne à trois lentilles: il en est question en 1662¹³⁹⁾; deux de ces verres étaient ‘proche l'un de l'autre’. En cette dernière année il parle de ‘bagatelles desia toutes vieilles¹⁴⁰⁾’. Il n'en veut plus rien savoir et fait son possible pour échapper à la nécessité d'en fabriquer pour son père qui voudrait en faire montre à la cour de Paris; il ne lui sied point, écrit le fils, ‘de faire jouer de telles marionettes au Louvre¹³⁹⁾’. Un peu plus tard Christiaan prétend¹⁵¹⁾: ‘Malgrè toute mon industrie et science je n'en puis venir a bout...il faut compter l'invention inter artes deperditas’. Des visiteurs avaient cependant jadis vu la lanterne chez lui à la Haye et continuaient à s'y intéresser. En novembre 1664¹⁴²⁾ P. Petit - l'ingénieur parisien bien connu (1598-1677) avec qui, soit dit en passant, il correspondait déjà avant 1660, aussi bien qu'avec Boulliau, tant sur les horloges que sur les lunettes - lui écrit: ‘mandez moi sil vous plaît la grandeur & proportion des deux verres que vous mistes & que vous jugez quil fault mettre a cette lanterne de peur¹⁴³⁾ etc.’; mais Huygens ne repond¹⁴²⁾ que vaguement, semble-t-il (nous ne possédons que la minute de la lettre) quoiqu'avec une figure assez semblable à celle dont nousavons parlé plus haut (toutefois, la ‘pictura pellucida’ n'y est pas indiquée): ‘Lanterne, il y a longtemps que les verres en sont ostez¹⁴⁴⁾ sans que je scache la mesure de tous...ma lanterne n'estoit pas bien ajustée. estoit sans miroir concave etc.’ Apparemment le feu sacré lui fait absolument défaut. De pareilles représentations sont désormais au-dessous de sa dignité. D'où venait donc l'intérêt nullement affaibli de son père pour la lanterne? Il nous semble qu'il y a lieu de songer ici à¹⁴¹⁾

138) T. XIII, p. 786, tirée du Manuscrit I.

139) T. IV, p. 111.

140) T. IV, p. 102.

139) T. IV, p. 111.

151) T. IV, p. 286.

142) T. IV, p. 266. La lettre n'est pas de 1662, mais de 1664, d'après la p. 601 du T. XIII. Cela paraît par le fait que Huygens y répondit le 11 décembre 1664, T. V, p. 161.

143) Cette désignation de la lanterne s'explique par le fait qu'on se servait parfois d'appareils de projection lumineuse pour effaroucher les gens. Il en est ainsi chez A. Klrcher ‘Ars magna lucis et umbrae’ (1646) - tout son livre X traite de ‘Magia’ (‘Magia catoptica’ etc.) - que Huygens connaissait depuis longtemps et son père également: la lettre à Mersenne où Constantijn en parle (T. II, p. 550) est déjà de novembre 1646. Voyez aussi la p. 357 du T.I. Mais la lanterne magique proprement dite avec des figures pellucides ne se trouve que dans la deuxième édition, de 1671, du livre de Kircher.

142) T. IV, p. 266. La lettre n'est pas de 1662, mais de 1664, d'après la p. 601 du T. XIII. Cela paraît par le fait que Huygens y répondit le 11 décembre 1664, T. V, p. 161.

144) Non pas ‘estez’ (faute d'impression).

141) T. IV, p. 197.

[p. 523]

l'influence de Drebbel qu'il avait connu et admiré à Londres dans sa jeunesse¹⁴⁵⁾ et qui, lui, n'avait aucun scrupule d'amuser la Cour par des représentations de ce genre: c'était pour lui un gagne-pain. Il est vrai que la lanterne magique n'est pas mentionnée par Constantyn dans la liste des choses remarquables qu'il apprit à connaître chez Drebbel¹⁴⁵⁾; il n'a sans doute pas assisté à des représentations de ce genre; mais parmi ses papiers se trouve encore aujourd'hui la lettre de Drebbel à Ysbrant van Rietwijck, datant probablement de 1608 ou 1609, où ‘le magicien’, pour parler avec les parents de Constantyn, donne la description, non pas il est vrai de l'appareil - rien ne démontre qu'il y aurait eu des figures pellucides - mais des merveilles qu'il montrait en ce temps¹⁴⁶⁾.

L'anneau que le magicien Christiaan avait découvert au firmament ne fut pas immédiatement reconnu véritable par tout-le monde. Plusieurs correspondants, il est vrai, l'acceptèrent; mais nous avons déjà dit plus haut que Boulliau doutait; Riccioli niait, toutefois sans rien publier; voyez la p. 185 du T. XV¹⁴⁷⁾. La seule attaque sérieuse fut celle d'Eustachio Divini (ou de Divinis) dans un écrit imprimé à Rome en 1660 dont en réalité, écrit P. Guisony, ‘le Père Fabry Jesuite François est l'autheur’¹⁴⁸⁾. La réplique de Huygens, la ‘Brevis Assertio Systematis Saturnii sui’ dédiée, comme la brochure de Divini, au prince Leopoldo, fut prête et imprimée en cette même année: il la publia à la Haye, chez Vlacq, avec une réimpression de la ‘Brevis Annotatio’ de Divini. ON trouvera l'un et l'autre écrit dans notre T. XV. Fabri - qui plus tard dut reconnaître son erreur - proposait au lieu de l'anneau un système de satellites bien compliqué. Il apparaît avec évidence qu'en ce moment la lunette de Huygens était supérieure à celles qu'on possédait en Italie. Plus tard, nous en reparlerons, les Italiens prirent leur revanche. N'étaient-ils pas même parvenus en 1660 à voir le satellite de Saturne? Huygens le prétend en critiquant les observations d'Eustachio¹⁴⁸⁾. En 1657 il avait écrit à de Sluse¹⁵⁰⁾: ‘Opticos tubos Eustachij Divini vehementer commendari video..quos utinam liceret cum nostris conferre. Gaudeo tamen eo perductos ut Saturni lunula Romae quoque jam conspiciatur’. Et en 1662 il reconnaît s'être plus ou moins trompé en 1660 puisqu'il écrit au prince¹⁴⁹⁾

145) Voyez les p. 420 et 449 qui précèdent.

145) Voyez les p. 420 et 449 qui précèdent.

146) Lettre publiée e.a. par F.M. Jaeger dans sa brochure ‘Cornelis Drebbel en zijne tijdgenooten’ de 1922. Jaeger dit à bon droit, nous semble-t-il, (p. 69) qu'il y est question d'une lanterne magique.

147) Avec la note 19.

148) T. XV, p. 392.

148) T. XV, p. 392.

150) T. II, p. 55.

149) T. XV, p. 442-447.

[p. 524]

Leopoldo¹⁵¹⁾ - qui le remercie de son ‘libretto’ déjà en septembre 1660¹⁵²⁾ en y ajoutant la figure d'une nouvelle grande lunette avec laquelle on pouvait voir le satellite (‘il pianetino’) et dit désirer grandement ‘di riconoscere la uerità’ sur le système de Saturne -: ‘Credo sane jam ab illo [Divini] comitem cerni, tot productis testibus, antea vero meritò dubitabam an vidisset cum nihil produceret nisi observationes quae cum rei veritate stare non poterant’.

Saturne, et les autres planètes, sont-elles habitées? Huygens n'avait parlé qu'en passant des Saturnicoles; il ne s'agissait pour le moment que d'une fiction servant uniquement à faire voir comment les choses se présenteraient à des observateurs placés sur la planète. Fabri et Eustachio ne manquent pas d'observer qu'une telle hypothèse est ridicule en soi et de plus en opposition aux dogmes catholiques¹⁵³⁾. Huygens répond brièvement n'y pouvoir voir rien de ridicule¹⁵⁴⁾. Mais ce n'est pas à l'âge de trente ans qu'un mathématicien ou naturaliste capable d'accomplir des tra vaux sérieux voudrait perdre son temps à discuter longuement l'inconnaissable.

151) T. IV, p. 286.

152) T. III, p. 129.

153) T. XV, p. 418-419.

154) T. XV, p. 462-463.