Oeuvres complètes. Tome XXI. Cosmologie
(1944)–Christiaan Huygens–
[pagina 413]
| |||||||
Observations de 1689Ga naar voetnoot1) sur quelques passages des ‘Principia’ de Newton, et nouvelles considérations de cette année sur le mouvement d'un corps punctiforme dans un milieu exerçant une résistance proportionnelle au carré de sa vitesse. | |||||||
[pagina 415]
| |||||||
Observations de 1689 sur quelques passages des ‘Principia’ de Newton, et nouvelles considérations de cette année sur le mouvement d'un corps punctiforme dans un milieu exerçant une résistance proportionnelle au carré de sa vitesse.§ 1. Theorema nostrum de centri gravitatis quiete vel aequali progressu perseverante demonstrare conatur Newtonus, et recte in corporibus ante concursum, sed non post. Cette observation est empruntée à la f. H 2 ou 10 r. du portefeuille LGa naar voetnoot1). Les feuilles de ce portefeuille traitent surtout de la question du ‘mouvement absolu’ ce qui suivant Huygens est une expression inadmissible; voyez sur ce sujet les p. 213 et suiv. du T. XVI. Huygens parle du Cor. IIII de Newton à ses trois ‘Axiomata sive Leges Motus’; nous avons déjà cité ces trois lois dans la note 1 de la p. 246 du T. XVI. Voici le corollaire en question: ‘Commune gravitatis centrum ab actionibus corporum inter se non mutat statum suum vel motus vel quietis, & propterea corporum omnium in se mutuo agentium (exclusis actionibus & impedimentis externis) commune centrum gravitatis vel quiescit vel movetur uniformiter in directum’. Dans les éditions suivantes, que Huygens n'a pas connues, ce texte a été modifié, mais le sens est resté le même. Ce n'est d'ailleurs pas de cet énoncé que Huygens parle mais seulement de la démonstration qui, dans la troisième édition, est encore exactement la même que dans la première. Il nous semble probable que ce qu'il entend critiquer sont plutôt les vues générales de Newton exprimées dans les lois et dans le célèbre Scholium qui les précède, où il est question e.a. du ‘Spatium absolutum’. | |||||||
[pagina 416]
| |||||||
Toutefois l'observation de Huygens - de date incertaineGa naar voetnoot2) - est trop brève pour qu'il nous soit possible de dire comment il eût pu s'exprimer s'il lui avait plu d'être plus explicite. Il est à remarquer que, quoiqu'il parle ici de ‘Theorema nostrum’, il n'a jamais donné une démonstration générale de ce ‘théorème’, comme nous l'avons déjà observé aux p. 24-25 du T. XVI, et qu'il a dû se contenter de dire (dans sa publication de 1669, T. XVI, p. 181) avoir remarqué une loy admirable de la nature ... qui semble estre generale [nous soulignons], c'est que le centre commun de gravité de deux ou de trois ou de tant qu'on voudra de corps [soustraits à toute influence extérieure] avance toûjours également vers le même costé en ligne droite devant et apres leur rencontre. On a vu dans le T. XVI (note 5 de la p. 221) qu'il a songé un moment à prendre la ‘loy admirable’ en question pour hypothèse, c.à.d. à la déclarer généralement indémontrable.
§ 2. Les observations de ce paragraphe ne contiennent pas de critique. Leur publication ne sert qu'à faire voir qu'en 1689 - comme auparavant; consultez p.e. dans notre T. IX le Rapport du 24 avril 1688 aux Directeurs de la Compagnie des Indes Orientales - Huygens étudiait les ‘Principia’ dont il reconnaissait la fort grande importance: consultez sur ce dernier sujet le § 12 de la p. 143 qui précède ainsi que le § 7 de la p. 310 du T. XIX et la p. 250 du T. XVI ainsi que la p. 475 qui suit.
Si super turri 200 pedibus alta horologium statuatur, erit ibi minor gravitas penduli, quae ad eam quam humi positum haberet erit ut aa ad qu. a + 200 hoc est aa + 400a + 40000. hoc est proxime ut a ad a + 400. Ergo sic quoque oscillationum celeritas. 19615737 ⫟ 400 - 86400 secunda in 24 horis /1¾″ uno die retardabitur. Ceci ne veut pas dire que Huygens est convaincu de l'existence de ce retard; comparez la p. 278 du T. XVII; il calcule seulement quel doit être le retard - p.e. pour une terre parfaitement sphérique - s'il est vrai, ce qui ne lui semble guère probable, que la loi de Newton est encore valable près de la surface de notre planète. Comparez sur ce sujet la partie H du présent § ainsi que les p. 439-440 qui suivent. | |||||||
[pagina 417]
| |||||||
BGa naar voetnoot4). Neutoni Coroll. prop. 10 lib. 1. La proposition enseigne qu'une force centripète agissant sur un corps et dirigée vers le centred'une ellipse parcourue par ce corps (punctiforme) doit, pour pouvoir causer ce mouvement, être proportionnelle à la distance du corps au dit centre. D'après le deuxième corollaire les périodes seront égales pour différentes ellipses ayant des grands axes égaux. Il devoit avoir montrè auparavant quelle raison il y doit avoir entre les celeritez du corps à l'endroit ou aboutissent les grands diametres des Ellipses, qui ont ces diametres egaux. Au reste ce corollaire est veritable. CGa naar voetnoot5). Ad propos. 6 lib. 1. NeutoniGa naar voetnoot6). Dicit vim centripetam in P esse reciproce ut solidum SP2 in QT2/QR [Fig. 118]. 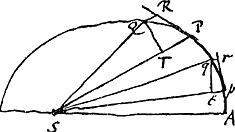 [Fig. 118].
Commentarium. Ut possit dicere reciproce, necesse est alterum insuper punctum poni vel intelligi ut p, in quo vis centripeta comparetur ad vim centripetam quae in P. Ut autem hae vires inter se conferantur, oportet spatia QSP, qSp aequalia esse; hoc est ▭ SP, QT aequale ▭o Sp, qt. tumque erunt vires centripetae sicut rectae minimae RQ ad rq. Nec video quid aliud sibi velit haec propositio; nam si dicit esse vim centripetam in P ad vim centripetam in p sicut Sp2 in qt2/rq ad SP2 in QT2/RQ, hoc est sicut RQ in Sp2 in qt2 ad rq in SP2 in QT2, haec ratio manifestè eadem est quae RQ ad rq, quia Sp.qt aequale SP.QT, adeoque sp2.qt2 aequale SP2.QT2. Quidui igitur dixit vis centrifugas in P et p esse ut RQ ad rq. aut quare potius eas esse reciproce ut SP2.QT2/QR ad Sp2.qt2/qr quam ut reciproce SP.Q.T/QR ad Sp.qt/qr vel ut reciproce SP3.QT3/QR ad Sp3.qt3/qr. | |||||||
[pagina 418]
| |||||||
An voluit positis spatijs QSP, qSp inaequalibus, comparare tamen vires centripetas in P et p. Hoc erat. Ponantur [Fig. 118bis] spatia aequalia SBA, SFE. n ⫟ s - t/ts/n. Ratio r ad y, quae est virium centripetarum in A et E, (positis spatijs aequalibus SBA, SFE) componitur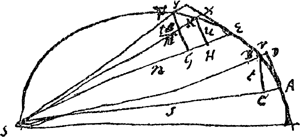 [Fig. 118bis]
ex ratione r ad x et x ad y. sed x ad y ut uu ad ttss/nn.  Ergo nnuu/x ⫟ ttss/r est ratio eadem quae r ad y hoc est quae vis centripetae in A ad vim centripetam in E. Et hoc vult propositio 6 lib. 1. Etsi dicat simpliciter vim centripetam esse ut ttss/r. Sed in praecipuis problematibus hac propositione non opus est. quando nimirum valor QR inveniri potest, et ▭ QT, SP datum ponitur.
DGa naar voetnoot7). Ad Prop. 9. l. 1.Ga naar voetnoot8) Spiralis haec semper appropinquat puncto S [Fig. 119], circumvolutionibus infinitis numero, nec unquam ad ipsum pervenit. ac tamen longitudinem certam non excedit. Demonstratio perobscura est, in qua cum dicit, mutetur jam utcunque angulus PSQ &c, hoc tantum propositum habet ut ostendat qualiscunque et ubicunque accipiatur angulus PSQ, semper QT2/QR esse ut SP. velut si accipiatur angulus major qSP, erit hic quoque qt2/qr ut SP. Nam quia QT2/QR ut SP, estque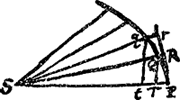 [Fig. 119]
qt2 ad QT2 ut qr ad QR, erit necessario et qt2/qr ut QT2/QR hoc est ut SP. | |||||||
[pagina 419]
| |||||||
Itaque cum semper sit QT2/QR ut SP, ducto utroque in SP2 erit QT2.SP2/QR ut SP3. ideoque per propos. 6, vis centripeta ut SP3 inversè. Poterat autem eundem angulum PSQ velut in duobus locis adsumtum considerasse, et utrobique similiter ductas PR, QT, QR. quae figurae proportionales fuissent. Et quia vis centrifuga ut QT2.SP2/QR inversè per 6. hoc autem ut SP3, quia QT ut SP, et ita quoque QR: erit et vis centripeta ut SP3 inverse. Demonstravi hanc eandem propositionem, ut propositione sexta nihil opus esset. | |||||||
Prop. 1.
Si mobile absque attractione gravitatis moveatur per medium resistens pro ratione celeritatis, celeritates reliquae post singula tempora aequalia sunt continue proportionales. 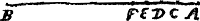 [Fig. 120]
Referatur celeritas in principio motus rectâ AB [Fig. 120]. Et post temporis particulam quandam, sit reliqua celeritas CB, amissa AC. Ergo cum resistentia sit ut celeritas diminuetur celeritas BC altera aequali temporis particula, quantitate CD quae sit ad AC sicut CB ad AB. cum effectus resistentiae sit ut vis. Quia ergo ut AB ad CB ita AC ad CD et permutando AB ad AC ut CB ad CD, etiam dividendo erit CB ad DB ut AB ad CB. Ergo continue proportionales AB, CB, DB. Eodemque modo de reliquis celeritatibus EB, FB, post singulas temporis particulas haec proportionalitas demonstrabitur. | |||||||
Prop. 2.Si mobile absque attractione gravitatis moveatur per medium resistens pro ratione celeritatis, erunt spatia temporibus aequalibus peracta in continua proportione geometrica. Cum enim celeritates initio singulorum temporum reliquae sint continue proportionales, si illis celeritatibus singula spatia aequabili motu peracta intelligantur, etiam spatia haec erunt continue proportionalia. Quum autem singulae illae temporis partes in particulas aequales innumeras dividi possint, simulque celeritates initio singularum sint totidem proportionales in continua serie, referent spatiola proportionalia singulis istis celeritatibus initio tempusculorum aequabili licet motu peracta, referent inquam spatia prioribus temporibus motu paulatim deficiente peracta. Cumque in singulis | |||||||
[pagina 420]
| |||||||
horum sit eadem particularum proportionalium multitudo, etiam componendo singulae erunt proportionales. Sic fere Neutonus propos. 2 lib. 2Ga naar voetnoot10). | |||||||
Prop. 3.Si fuerit divisa linea AB [Fig. 120] in particulas continue proportionales quotcunque, puta decem, et mobile, per medium resistens in ratione celeritatum certo tempore percurrat motu horizontali lineam totam; prima vero decima temporis ejus particula peragat primam ac maximam particulam AC, etiam sequentibus aequalibus temporis particulis singulas reliquas lineae particulas peraget. Quia enim aequales temporis particulae ponuntur erunt per praecedentem, spatia ijs temporibus peracta continue proportionalia. Atqui linea AB non potest in partes decem continue proportionales dividi, quarum maxima sit AC, nisi uno modo. Ergo cum decem temporibus aequalibus qualium uno peracta est AC, tota AB [percurri] tur, ne [cesse est] ut sing [ulis reliquorum] temporum peragantur particulae illae proportionales in quas divisa est AB. FGa naar voetnoot11). Ad prop. 5 l. 2. NeutoniGa naar voetnoot12). Resistentia medij est in duplicata ratione celeritatis. Demonstrat, sed obscure admodum, quod hyperbole est ejus naturae ut acceptis partibus aequalibus in asymptoto, indeque excitatis parallelis perpendicularibus quae hyperbolae occurrant, harum differentiae decrescunt in duplicata ratione ipsarum sibi proximarum. quod hoc calculo verum esse invenio. 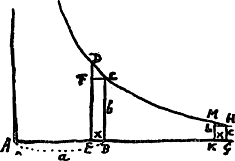 [Fig. 121]
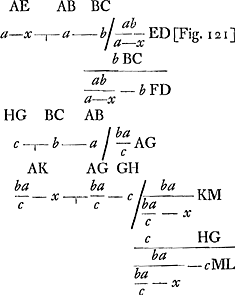 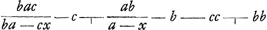
| |||||||
[pagina 421]
| |||||||
Cette équation se montre vraie attendu que dans le cours du calcul quia x minima est deleri possunt in quibus xx. Hinc autem sequitur (quod miror Neutonum non observasse) corpus horizontali motu incitatum, etiam in medio resistente infinitum spatium conficere infinito temporeGa naar voetnoot13). quod contra est cum resistentia est ut velocitas, ut ostendiGa naar voetnoot14). Illud mirabile prorsus videtur. Cogita enim globum plumbeum sub aqua in plano horizontali projectum an in infinitum spatium perget moveri? GGa naar voetnoot15). Ad prop. 6. l. 2 NewtoniGa naar voetnoot16). 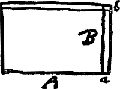 [Fig. 122]
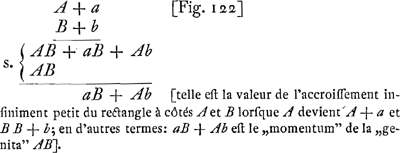 | |||||||
[pagina 422]
| |||||||
[Le carré b2 étant reprénté par a, dont x est l'accroissement, tandis que celui de b est c, on a]
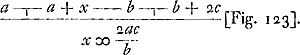 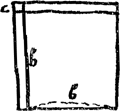 [Fig. 123]
Sed a ut bb. Ergo x ut 2bc. 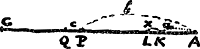 [Fig. 124]
Censetur quadratum AQ [Fig. 124] excedere quadratum AP duplo rectangulo APQ, neglecto minimo quadrato ex PQ. Hinc statim concludi potest rectae AK incrementa minima esse ut 1 APQ. 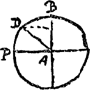 [Fig. 125]
H.Ga naar voetnoot17) 1/578 [d'après Huygens; voyez les p. 390 et suiv. qui précèdent] Excessus AB super AP [Fig. 125] in tellure. 1/289 differentia ponderis in B et P, itemque longitudinis [penduli]. Differentia ponderis est proxime dupla differentiae distantiarum, quia pondera leviora fiunt in duplicata ratione distantiarum [suivant ce que Huygens semble considérer ici comme la loi de Newton; ceci ne veut pas dire que Huygens accepte sans critique ce qu'il propose ici; comparez notre remarque à la partie A qui précède et voyez aussi le calcul de la p. 476 du ‘Discours de la Cause de la Pesanteur’ où Huygens dit douter fort de l'existence ‘aux pendules d'une autre inégalité,’ c.à.d. autre que celle provenant de la force centrifuge]. Est differentiae ponderis aequalis curtatio penduli, hoc est talis pars longitudinis totius. Atqui defectus diurnus temporis penduli non curtati ad totius dici tempus est proxime ut ½ curtatio penduli ad totum pendulum. Ergo defectus diurnus venientis horologij ex P in B ad 24 horarum tempus, ut differentia distantiarum AB, AP ad AB. 1/578 differentia retardationis in B Si veniat horologium ex P. 3600″ in hora ... 86400″ in die [86400/578 ...] 149″. tot secundis deberet horologium sub Polo recte compositum retardari sub aequatore ex sola caufa distantiae majoris a centro eoque minoris gravitatis; praeter retardationem ex vi centrifuga quae 150″ efficit. Sed in locis intermedijs ut D nequaquam tantum efficiet haec distantiarum differentia quantum vis centrifuga. | |||||||
[pagina 423]
| |||||||
§ 3. Dans le Manuscrit G les feuilles 11, 12, 15 et 16 de 1689, d'où nous avons tiré les parties A, B, C, D et G du § 2, sont suivies de deux autres de la même année où Huygens reprend ses calculs de 1668 (T. XIX, p. 102-119 et 144-157) sur les corps en mouvement dans des milieux qui leur résistent proportionnellement soit à leurs vitesses soit aux carrés de leurs vitesses. Ou plutôt: il ne considère ici que ce deuxième cas. Dans l'‘Addition’ au ‘Discours de la Cause de la Pesanteur’ (édition de 1690) Huygens dira expressément (p. 482 qui suit) que ‘ce n'est qu'à l'occasion du Traité de Mr. Newton’ qu'il a repris l'étude de la théorie de la résistance. Il s'agit, comme chez Huygens en 1668 et comme chez Newton dans les propositions considérées au § 2 qui précède, de corps punctiformes. Ce ne fut qu'en 1691 que Huygens mit définitivement au net dans ies p. 75-81 du Manuscrit G, en tenant aussi compte des résultats de Newton, sa théorie de 1668 ‘de descensu [verticali] corporum gravium [corps punctiformes] et ascensu [verticali] per aerem aut materiam aliam, quae resistit motui in ratione duplicata celeritatum, ut revera contingit’; nous avons reproduit ces pages aux p. 23-45 du T. X. Ici nous ne tenons compte, partiellement, que du texte des p. 17v-18r du Manuscrit dont il était question plus haut. Huygens fait voir qu'il n'est pas permis, comme c'était généralement le cas lorsque la résistance était proportionnelle à la vitesse (T. XIX, p. 80 et p. 113, note 13), de décomposer le mouvement, c.à.d. tant la vitesse initiale que la résistance, suivant deux axes perpendiculaires entr'eux. Dans la Fig. 127 les trois droites AK, AL, AB, dont AL et AB sont les deux axes nommés, sont situées par hypothèse dans un plan horizontal. La véritable longueur parcourue sur la droite donnée se montrera ne pas étre la résultante des longueurs parcourues sur les deux axes. Aγ [Fig. 128] étant la distance parcourue sur la droite AL en un temps donné, il suffira de faire voir que la distance Aδ parcourue en ce temps sur la droite AK faisant avec AL un angle de 45o est inférieure à Aζ. Ejusdem globi eadem debet esse celeritas terminalis in medio resistente in duplicata 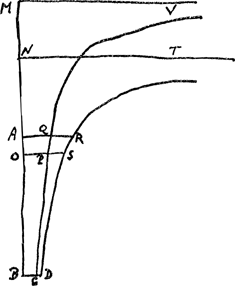 [Fig. 126]
ratione celeritatis ac si idem in simplici ratione celeritatis resisteret. Certa enim quaedam celeritas flatus sursum sustinere valebit globum ne decidat. quam proinde globus habere debebit ne amplius casum acceleret. Ea vis ferentis aeris aequipollet gravitati. Sed sciendum posteriorem hypothesin esse impossibilem. Etsi forsan alîius generis impedimentum inveniri possit quod est ut celeritas.
Cum celeritas incipiens per AK [Fig. 127] ad celeritatem incipientem per AL est ut AK ad AL, tunc resistentia aeris et amissio celeritatis in prima temporis particula per AK est ad resistentiam et amissionem celeritatis in eadem temporis particula per AL ut qu. AK ad qu. AL, hoc est ut 2 ad 1. Si AR ad AQ [Fig. 126] ut √2 ad 1, et AB ∞ AM, erit spatium RABD ad spatium | |||||||
[pagina 424]
| |||||||
QABC ut iter globi in recta AK [Fig. 127] inceptum celeritate AK ad iter globi in recta AL inceptum celeritate AL terminali; eodem nempe tempore AB. Sunt autem spatia ilia ut logarithmus rationis AR ad BD ad logarithmum rationis AQ ad BC. hoc est ut logar. rationis BN ad NA ad logar. rationis BM ad MA. hoc est ut log. rationis
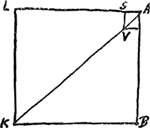 [Fig. 127]
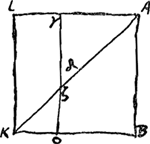 [Fig. 128]
2 + √2 ad √2, ad log. rationis 2 ad 1, sive log. 2 ... apparet eandem esse hyperbolam RS et QP seu motâ asymptoto MV in NT. ut sicut RA ad QA ita sit MA ad NA.
Ceci s'explique le mieux par la considération de l'équation du mouvement dv/dt = - kv2, où v est la vitesse, t le temps, et k une constante. Pour le mouvement suivant AL (ou suivant AB) la vitesse initiale est par hypothèse la ‘celeritas terminalis’ d'une chute verticale, c.à.d. √g/k, où g est l'accélération de la pesanteur. Pour le mouvement suivant AK la vitesse initiale est donc √2g/k. Appelant généralement vo la vitesse initiale on a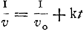 ou ou 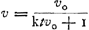 , d'où la distance parcourues , d'où la distance parcourues
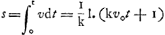 , l. étant le logarithme népérien.
Pour les mouvements suivant AK et AL on a donc respectivement , l. étant le logarithme népérien.
Pour les mouvements suivant AK et AL on a donc respectivement 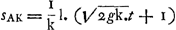 et et 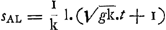 . En disant que ‘spatia illa’ sont entr'eux comme log. AR/BD à log. AQ/BC ou . En disant que ‘spatia illa’ sont entr'eux comme log. AR/BD à log. AQ/BC ou 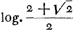 à log. 2/1, Huygens prend tant les grandeurs g et k que le temps considéré t égaux à une même droite qui a l'unité de longueur. Ou voit qu'on trouve en effet dans cette supposition à log. 2/1, Huygens prend tant les grandeurs g et k que le temps considéré t égaux à une même droite qui a l'unité de longueur. Ou voit qu'on trouve en effet dans cette supposition 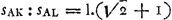 : l. 2; puisqu'il s'agit de rapports, peu importe que ce soit le logarithme népérien qu'on confidère ou, comme Huygens, celui à base 10.
L'équation : l. 2; puisqu'il s'agit de rapports, peu importe que ce soit le logarithme népérien qu'on confidère ou, comme Huygens, celui à base 10.
L'équation 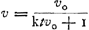 montre aussi que la relation entre les vitesses et les temps se représente graphiquement par une hyperbole équilatère [Fig. 126], et que les deux hyperboles correspondant aux mouvements suivant AK et AL respectivement, savoir montre aussi que la relation entre les vitesses et les temps se représente graphiquement par une hyperbole équilatère [Fig. 126], et que les deux hyperboles correspondant aux mouvements suivant AK et AL respectivement, savoir 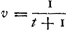 et et 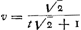 ou ou
| |||||||
[pagina 425]
| |||||||
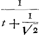 , sont identiques ou plutôt ne diffèrent qu'en position. Dans la Fig. 126 AR et les autres droites horizontales représentent des vitesses; MB étant l'axe des temps l'espace ARDB p.e. correspond à une intégrale ∫ et représente donc une distance parcourue; or, il était bien connu que de pareils espaces sont entr'eux comme des logarithmesGa naar voetnoot18). , sont identiques ou plutôt ne diffèrent qu'en position. Dans la Fig. 126 AR et les autres droites horizontales représentent des vitesses; MB étant l'axe des temps l'espace ARDB p.e. correspond à une intégrale ∫ et représente donc une distance parcourue; or, il était bien connu que de pareils espaces sont entr'eux comme des logarithmesGa naar voetnoot18).
Tempore toto AB ... pervenit in recta AL horizontalis tabulae, incipiens in A celeritate terminali, usque ad γ [Fig. 128], sumta Aγ ∞ BO. Eodem vero tempore in recta AK, incipiens celeritate quae sit ad terminalem ut √2 ad 1, perveniet ad δ, sumta Aδ secundum inventa pagina praecedenti. Nota quod deficiens spatium δK in recta AK non est duplum γL spatii desicientis in recta AL [il faut lire: que δ K n'est pas égal à γL √2], sicut esset si celeritas diminuta in AK et AL eodem tempore, maneret semper in ratione √2 ad 1, seu AR ad AQ in figura paginae praecedentis [Fig. 126]. Set ea ratio minuitur paulatim, sicut apparet quod DB ad CB minorem habet necessario quam AR ad AQ. On le voit aussi par les formules: le rapport des vitesses suivant AK et AL respectivement est représenté par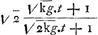 , expression dont la valeur décroît constamment lorsque t augmente. , expression dont la valeur décroît constamment lorsque t augmente.
Si possemus considerare (in hac resistentia quae est in dupla ratione celeritatum) motum per AK tanquam compositum ex motu per AB et per AL, deberet tempore AB pervenisse mobile ex A in ζ in diagonio. Sed pervenit in δ. Ergo non habet hic locum motus compositio.
§ 4. En publiant en 1701Ga naar voetnoot19) son ‘Historia Cycloeidis qua genesis & proprietates lineae cycloeidalis praecipuae ... recensentur, etc.’ Joh. Gröningius y ajoutait ce qu'il appelle ‘Christiani Hugenii Annotata posthuma in Isaaci Newtoni Philosophiae Naturalis Principia Mathematica’. Nous avons déjà dit au T. XGa naar voetnoot20) que ce titre est décevantGa naar voetnoot21): quoique le manuscrit de ces ‘Annotata’ - conservé à Hannovre - soit de la main de Huygens, ce ne sont pas cependant pour la plupart des remarques provenant de lui. Il a copié des remarques de Fatio de Duillier, et de Newton, de plusieurs desquelles ce dernier a fait usage dans la deuxième édition des ‘Principia’. Cela paraît d'ailleurs chez Gröningius lui-même puisqu'en deux endroits (p. 110 et 128) il écrit entre parenthèses: ‘addit Hugenius ...’ et ‘in margine adscripsit Hugenuis...’; nous ne reproduisons pas ici ces deux passagesGa naar voetnoot22) à cause de leur insignifiance. Les ‘Annotata’ débutent cependant par une remar- | |||||||
[pagina 426]
| |||||||
que qui est bien de Huygens: c'est notre No 2542 de la p. 329 du T. IX: Huygens pensait à tort que Newton avait admis dans le cas d'une résistance proportionnelle au carré de la vitesse la composition des mouvements dont il était question (pour un plan horizontal) au § 3. On trouve ensuite chez Gröningius les Pièces de Newton qui constituent nos No 2540 et 2541 (T. IX, p. 321 et 328). Dans le T. IX nous avons attribué à Huygens lui-même la remarque (No 2543) sur la ‘aqua effluens’. Ce qui suit chez Gröningius (p. 113-116) et se rapporte aussi à ce dernier sujet se trouve dans notre édition aux p. 154-155 du T. X. Viennent ensuite les remarques de Fatio ‘Conjecturae de sphalmatis typographicis etc.’ que nous avons publiées, plus complètement que Gröningius, aux p. 147-155 du T. X. |
|

