Oeuvres complètes. Tome XXI. Cosmologie

[p. 133]

Projet de 1680-1681, partiellement exécuté à Paris, d'un planétaire tenant compte de la variation des vitesses des planètes dans leurs orbites supposées elliptiques ou circulaires, et considération de diverses hypothèses sur cette variation.

§ 1¹⁾.

Major diameter ellipsis	Mercurij	ad minorem ut	1000 ad 978.
Major diameter ellipsis	Martis	ad minorem ut	1000 ad 996.
Major diameter ellipsis	Jovis	ad minorem ut	10000 ad 9988.
Major diameter ellipsis	Saturni	ad minorem ut	1000 ad 998.

Comparez la première table du § 15 qui suit où figurent aussi la Terre et Vénus.

Les nombres du présent § s'accordent exactement avec les données du § 15 qui suit excepté dans le cas de Saturne: pour cette planète le rapport ici considéré devrait être ‘ut 10000 ad 9984’

1) Manuscrit F, p. 5. Voyez sur la date la note 11 de la p. 138.

§ 2.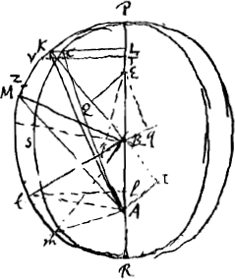

[Fig. 34]

Comme nous l'avons dit dans l'Avertissemen. nous intercalons ici une page (f. 14 r) du Manuscrit G, datant de septembre 1690.

In Kepleri hypothesi ex anomalia mediat invenire anomaliam excentri et coequatam tentando (alternis excedet justam magnitudinem et ab ea deficiet).

Sit PCS [Fig. 34] Orbita Planetae Elliptica. B centrum, A focus in quo Sol. Focus alter E. Sit etiam diametro PR circumscriptus ellipsi circulus PMR. In quo arcus PM designet motum seu anomaliam mediam ab aphelio P, puta 60 gr. Quod si jam in ellipsi ita duci possit AC ut area PAC sit ad totam Ellipsin sicut sector PBM ad totum circulum; erit tunc C locus planetae, et angulus PAR ille quem vocat anomaliam coequatam.

[p. 134]

Quia autem ductâ KCL, in axem PR perpendiculari, eandem rationem habet area PAK ad circulum totum quam area PAC ad ellipsin: Requiritur tantùm ut ita ducatur AK, ut area PAK sit aequalis sectori PBM. Tunc arcus PK erit anomalia Eccentri Kepleriana. Componitur autem area PAK ex sectore PBK et triangulo BAK; quorum quidem sector PBK aequatur ½ ▭^o ex arcu PK in radium BR, triangulus vero BAK aequatur ½ ▭ AB, KL sive ½ EQ in BK, ducta scilicet ex E foco perpendiculari EQ in BK. Nam ut BK ad KL ita AB seu BE ad EQ. Si igitur EQ esset aequalis arcui KM, jam area PAK aequalis esset sectori PBM, quod quaerebatur. Porro quia ut BK ad AB, ita KL ad EQ; estque proportio data ac constans BK ad AB; erit et EQ semper pars eadem sinus KL. Oportet igitur invenire arcum PK talem, ut addita ex parte proportionali sinus sui KL, secundum rationem BA ad BK vel BR, hoc est secundum rationem excentricitatis ad dimidium axem, summa fiat aequalis arcui anomaliae mediae datae.

Hoc autem fit tentando. Et si nimius adsumtus fuit arcus PK, auferendo ab eo inventum excessum, vel si nimis parvus fuit adsumtus, addendo defectum. Statim enim admodum prope ad verum devenitur, quia in planetis omnibus excentricitas exigua est ratione semiaxis. Nam si exempli gratia arcus PK aequo minor fuerit inventus, defectu ZM, eumque in secunda positione addam arcui PK ponendo KV ∞ ZM, ut sit jam arcus PV, jam quidem hic, una cum parte proportionali, qualem diximus, sinus KL, aequalis erit arcui PM; sed idem arcus PV una cum parte proportionali sinus sui VT, paulum excedet arcum PM, quanto scilicet pars ista proportionalis sinus VT superat partem proportionalem sinus KL quod exiguum est. Et si rursus excessus hic exiguus auferatur ab arcu PV, devenietur ad differentiolam deficientem multo minorem. Decrescent enim hae defectuum et excessuum differentiolae fere secundum rationem compositam ex KB ad BL et KB seu RB ad BA. Est autem BA pars exigua BR in omnibus Planetarum orbibus.

Aliter possumus sinum KL ducere in BA, et productum, hoc est, duplum trianguli KBA, dividere per BK, unde facta AI debet aequari arcui KM. reductis nempe gradibus secundum dimensionem circumferentiae. atque hoc eodem redit quo praecedens methodus. quoque etiam Kepleriana pag. 696 Epit. astron.²⁾ Sed ille longior et obscurus, nec explicat causam approximationis.

2) ‘Epitome Astronomiae Copernicanae, Vsitatâ formâ Quaestionum & Responsionum conscripta, inque VII. Libros digesta. Etc.’. Authore Ioanne Keplero etc. Francofurti, Imp. I.G. Schönwetteri MDCXXXV. C'est en effet à la p. 696 où se termine le chapitre du Lib. V ‘De angulo ad solem. Doce computare anomaliam coaequatam seu angulum ad solem’, que l'on trouve une figure semblable à celle de la présente Pièce et les calculs correspondants.

[p. 135]

§ 3³⁾. De hypothesi Bullialdi⁴⁾.

Conum scalenum invenire et in eo sectionem datae ellipsi similem et aequalem, cujus focorum alter sit in coni diametro.

Sit Ellipsis ACB, cujus axis AB, minor diameter LC [Fig. 35]. Sit ADB semicirculus.

[Fig. 35]

CD parallela AB. DE parallela CL. Secet FEG rectam AB, quocumque angulo inclinata. Sintque EF, EG singulae aequales AL vel LB. Et ducantur AF, GB, concurrentes in H. Sitque QR parallela AB. Erit jam conus quaesitus QHR, cujus axis HLK, sectionis ellipticae diameter major FG. focorum alter P ubi HK secat FG. Ipsaque ellipsis similis et aequalis datae ACB.

Ducatur enim FN parallela AB, et secans HK in M. item FO parallela HK. Quia ergo FG bifariam secta est in E, erit EB aequalis ½ FN, hoc est ipsi FM, hoc est OL. Quare addita communi LE, erit OE aequalis LB sive EF. unde et PF aequalis OL sive EB. Est autem rectangulum AEB hoc est qu. ED aequale quadrato minoris axis ellipseos FG. ideoque minor hic axis aequalis ED sive LC. Sed et axis FG aequalis ex constructione axi AB. Ergo ellipsis FG similis et aequalis ellipsi ACB. Sed E est focus ellipsis ACB quia CE aequalis LD sive LB. Ergo cum FP sit aequalis EB erit et P focus ellipsis FG.

3) Manuscrit F, p. 9 et 10.

4) Voyez l'Avertissement sur les ouvrages de Boulliau et de Seth Ward se rapportant à cette hypothèse.

[p. 136]

[Fig. 36]

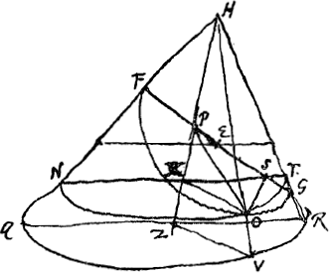
Collocata elliptica planetae orbita FG in cono uti dictum. hypothesis Bullialdi est moveri planetam per lineam ellipticam FOG [Fig. 36], hoc modo ut semper sit in recta quae altera extremitate manet in coni vertice H, altera aequabili motu circumducitur per circonferentiam basis QR. Unde si planeta sit in puncto aliquo orbitae ellipticae O ducta ex vertice ad basin recta HOV, angulus QZV erit angulus anomaliae mediae.

Demonstrat autem Wardus, ducta PO ex foco ellipsis qui est in axe HZ, angulum FPO aequari angulo QZV. ideoque hypothesin Bullialdi eandem esse atque illam quae aequabilem planetae motum tribuit circa ellipticae orbitae focorum alterum, dum alter focus ponitur locus solis.

En marge: Demonstratio Wardi. Sit OS perpend. in NT, et NOT sectio coni basi parallela secans axem HZ in X, et jungatur OX. Erit eadem OS perpend. in FG, quia est perpend. in planum per axem QRH. In triangulis igitur rectangulis PSO, XSO aequales sunt PS ipsi XS per praeced. et SO communis, unde angulus OPS aequalis OXS, ac proinde FPO aequ. NXO sive QZV.

[Fig. 37]

Cum haec sit Bullialdi hypothesis, nescio cur Mercator dicat⁵⁾ Bullialdum limitationem quandam addidisse quae est hujusmodi. (En marge: Limitationem hanc inveni in responsione Bullialdi ad ea quae S. Wardus objecerat.) Sit angulus FPO [Fig. 37] anomalia media, LOB perpend. axi FG, quae secet circonferentiam FBG in B, unde ducta BP ad focum P, secet ellipticam planetae orbitam in C. Erit, ex limitatione ista, planeta in C, qui alioqui futurus erat in O.

Dicit autem Bullialdus effecisse ut calculus suus satisfaceret observatis, hypothesin vero, quam Bullialdi veram esse ostendimus, à coelo aberrare saepius affirmat, atque in Marte quidem ad gradus semissem ferè.

5) Voyez la note 25 de la p. 141 qui suit.

[p. 137]

§ 4⁶⁾.

BP radius 100000 [Fig. 38 et 39]. BA vel BE excentricitas 9265 in Marte.

[Fig. 38]

[Fig. 39]

1745,33 gradus 1 in partibus⁷⁾.

Anomaliae mediae 90^o. convenit anomalia eccentri PK gr. 84^o43′ secundum hypothesin Kepleri. At secundum hypothesin Wardi PK est 84^o41′ cadente perpendiculari KL in E focum, quia angulus PEK anomaliae mediae secundum hanc hypothesin est 90^o8).

Voyez l'Avertissement qui précède sur les équations qui expriment les hypothèses de Kepler et de Ward.

Sit rursus anomalia media data 45^o. quaeritur [selon l'hypothèse de Kepler] arcus PK anomaliae excentri. Oportet invenire arcum PK qui additus ad rectam quae sit ad sinum KL ut AB ad BR, faciat summam aequalem arcui 45 gr.⁹⁾.

¹⁰⁾

6) Manuscrit E p. 263 (dernière page du Manuscrit). À la p. 239 serrouve la date du 11 mai 1680.

7) C.à.d. πr/180, où r = 100000, = 1745,33.

8) Voyez sur les calculs suivant l'hypothèse de Ward le § 5 qui suit.

9) Première équation de Kepler, comme nous l'avons dit aussi à la p. 116 qui précède, en parlant du présent calcul.

10) Huygens calcule ce nombre à l'aide de logarithmes.

[p. 138]

On voit que Huygens résout la première équation de Kepler ‘tentando’: après avoir pris 40^o pour l'‘anomalia eccentri’ A_e il prend maintenant 41^o. Il trouve ainsi PK 41^o28 secundum Keplerum.

Il calcule ensuite que cet arc PK ou angle A_e vaut 41^o22′ sec. Ward⁸⁾.

8) Voyez sur les calculs suivant l'hypothèse de Ward le § 5 qui suit.

§ 5¹¹⁾.

Theorema trigonometricum utile ad inveniendam anomaliam coequatam ex anomalia media in hypothesi Wardi et Pagani¹²⁾ Elliptica. quae eadem et Bullialdi.

ABC triangulum. Erit ut summa laterum AB, BC ad eorum differentiam ita tangens dimidiae summae angulorum A, C, ad tangentem dimidiae ipsorum differentiae.

Nous avons déjà publié à la p. 457 du T. XX la démonstration donnée ici par Huygens de ce théorème trigonométrique.

[Fig. 40]

Data anomalia media¹³⁾, invenire coequatam¹⁴⁾, hoc est dato angulo. PEC [Fig. 40] motus aequabilis planetae circa focum ellipsis E, invenire angulum CAE, qui et angulus ad solem vocatur, quia in A sol statuitur, C est planeta [suivant l'hypothèse de Ward ou, si l'on veut, de Boulliau et de Ward]. Producatur EC ut sit CS aequalis CA. Est ergo angulus CEP summa duorum ESA, EAS. angulus vero CAE aequalis differentiae eorundem, quia CAS aequalis CSA.

Ergo ex theoremate praecedente ut ES + EA ad ES - EA ita tang. ½ CEP ad tang. ½ CAP. Sed ES + EA aequ. 2 AP quia ES ∞ EC + CA sive ∞ PR, cui addita EA fit 2 AP. At ES - EA aequatur duplae AR. Ergo ut 2 AP ad 2 AR sive ut AP ad AR ita tang. ½ CEP ad tang. ½ CAP. Est autem ratio AP ad AR constans ac perpetua in singulis

11) Manuscrit F, p. 3 et 4. Toutes les dates (peu nombreuses) sont de 1680 (la première étant celle du 16 novembre 1680 à la p. 39) jusqu'à la p. 45 inclusivement (27 décembre 1680). Voyez aussi la note 6 de la p. 137. La p. 55 porte la date du 16 février 1681.

12) Il est question de l'ouvrage de 1657 de Bl. F. de Pagan publié à Paris et intitulé ‘Tractatus de theoria planetarum, in quo omnes orbes coelestes geometrice ordinantur contra sententiam communem astronomorum’.

13) Désignée dans les équations de l'Avertissement par A_m.

14) Désignée dans les équations de l'Avertissement par A_c.

[p. 139]

planetarum orbitis. Ergo ad inveniendum angulum CAP, opus solummodo ut logarithmus rationis PA ad AR, hoc est differentia logarithmorum PA, AR, auferatur

[Fig. 41]

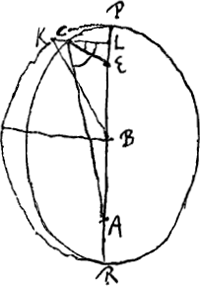
à logarithmo tangentis ½ anguli CEP. Nam reliquum erit log. tang. ½ anguli CAP.

§ 6. PKR [Fig. 41] est semicirculus, KCL perpend. PR. Volo ex cognitis angulis CEP, CAP, invenire arcum PK quem Keplerus vocat anomaliam Excentri.

Deinde ex eadem anomalia media data 45^o inveniam secundum hypothesin Kepleri eundem arcum PK ut pateat differentia quae hic est inter hypotheses Wardi et Kepleri.

Exempli gratia in Mercurij orbita. BP est ad excentric. BE ut 100,000 ad 21,000 secundum Keplerum. Ergo PA ad AR ut 121000 ad 79000 sive ut 121 ad 79.

^15)16)17)

15) C'est le logarithme de , où a désigne le demi grand axe de l'ellipse et c son excentricité linéaire.

16) Voyez ce que nous disons sur ce calcul à la p. 121 qui précède.

17) Il y a ici une erreur de calcul, comme nous l'avons dit aussi aux p. 121 et 127 qui précèdent. Comparez la note 20 qui suit.

[p. 140]

§ 7¹⁸⁾.

Regula [Kepleri] est in fine libri E¹⁹⁾. Inveniatur arcus PK ejusmodi ut additus parti sui sinus quae sit ad ipsum sinum sicut BA ad BR, summa aequetur ipsi arcui anomaliae mediae datae. hoc autem fit tentando, et excessum vel defectum in primo tentamine inventum auferendo vel addendo arcui adsumto.

In praecedente exemplo [§ 6] (ponitur hic anomalia media 45 gr.) semel tentasse sufficit²⁰⁾ quia prima adsumtio 37^o jam proxima erat verae.

37. 46^20)	arcus PK sec. hyp. Kepleri
37. 0	arcus PK sec. hyp. Wardi
_____
46′	differentia arcuum PK
37^o 38′	arcus PK mihi
8′	differo a Keplero, hoc est secundum viam eam quam in automato secutus sum^21).

18) Manuscrit F, p. 5.

19) Comparez le § 4 qui précède.

20) Voyez la note 17 qui précède. L'erreur de calcul s'explique, comme on voit, par le fait que Huygens a fait l'interpolation d'une manière trop grossière.

20) Voyez la note 17 qui précède. L'erreur de calcul s'explique, comme on voit, par le fait que Huygens a fait l'interpolation d'une manière trop grossière.

21) Nous avons cité ces dernières paroles à la p. 122 de l'Avertissement.

§ 8²²⁾

[Fig. 42]

Sit anomalia media 90^o, nempe angulus PEK [Fig. 42]. Ergo ad inveniendum arcum PK in hypothesi Wardi; quia BK est 100000 et EB 21000, erit arcus KP aequalis complemento arcus cujus

Etc. Nous ne croyons pas devoir reproduire tous les calculs des p. 4-6 du Manuscrit.

Exemplum Kepleri p. 696²³⁾. Examinatur mea methodo ut quantum intersit appareat. Datur anomalia media, hoc est arcus KAP 50^o.9′.10″. invenienda est anomalia excentri PK arcus.

22) Manuscrit F, p. 5 et 6.

23) De l'‘Epitome Astronomiae Copernicanae’. Comparez sur cette p. 696 la fin du § 2 qui précède.

[p. 141]

§ 9²⁴⁾.

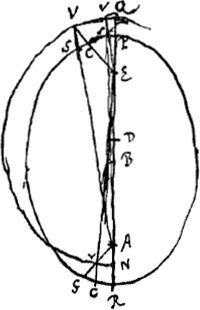[Fig. 43]

AE [Fig. 43] distantia focorum secta in D media et extrema ratione secundum hypothesin Mercatoris²⁵⁾. Rad. DQ, DN ∞ BP, BR. Quaero an eandem rationem celeritatum in P et R faciat quam Wardus et Keplerus.

Invenio celeritatem in R ad celeritatem in P paulo majorem fieri ex hypothesi Mercatoris. sed perexigua differentia.

Voluissem minorem eam proportionem fuisse nam hoc naturae convenientius si motum materiae vorticis solaris spectemus; qui facit celeritates planetarum duorum in ratione contraria subduplicata distantiarum. At Keplerus et Wardus in ipsa ratione contraria distantiarum faciunt celeritates ejusdem planetae. Mercator in paulo majore. Mirum in his hypothesibus qui possit materia vorticis conferre motum planetae perihelio, suo ipsius motu celeriorem²⁶⁾.

²⁷⁾

24) Manuscrit F, p. 7.

25) Voyez sur les ouvrages astronomiques de N. Mercator et sur son hypothèse les notes 33 et 34 de la p. 120 qui précède.
Au sujet de l'hypothèse de Ward Mercator écrit à la fin du Cap. XXI du Lib. II de ses ‘Institutiones astronomicae’: ‘Neque intra pauca minuta continetur iste dissensus à coelo, sed in Marte aliquando ad dimidium ferè gradum ascendere potest, id quod nemo unquam observationum vitio adscripserit. Neque latuit Keplerum, hoc incommodum secuturum ordinationem motûs aequabilis circa focum superiorem, qui dixerat in suâ epitome, eam ferè sic accipi posse; verùm illud ferè tantam habebat latitudinem, ut ab illo abstinendum sibi duxerit’.

26) Nous avons cité cette sentence à la p. 121 de l'Avertissement qui précède.

27) Le soleil se trouve au foyer A de l'ellipse PSR. Le rayon vecteur EV tourne uniformément



autour du deuxième foyer E. B est le centre de l'ellipse. On peut se figurer que D est le point qui divise AE en moyenne et extrême raison. V est un point de la circonférence de cercle décrite du centre D avec le rayon a (demi grand axe). La planète se trouve par hypothèse en S, point d'intersection de la droite VA avec l'ellipse. La vitesse de la planète à l'aphélie P est v₁ = PP′/t, t étant le temps infiniment court pendant lequel le rayon vecteur tourne de EQ en EQ′ (Q et Q′ se trouvant sur la circonférence de cercle). De même v₂ = RR′/t est la vitesse au périhélie. Le mouvement correspondant à RR′ du rayon vecteur est de EN en EN′ (N et N′ se trouvant sur la circonférence de cercle). On a v₁ : v₂ = PP′ : RR′. Or, PP′ : QQ′ = PA : QA et RR′ : NN′ = AR : AN. Donc v₁ : v₂ = QQ′.PA.AN : NN′.AR.QA. Mais QQ′ : NN′ = QE : NE. Donc v₁/v₂ = PA/QA.AN/AR.QE/NE.

[p. 142]

§ 10²⁸⁾.

Ex diametris apparentibus solis è terra perihelia et aphelia determinanda esset proportio harum distantiarum. Deinde motus terrae in 7 vel 8 diebus inveniendus in utraque distantia ope horologiorum et calculi, observando quanto tempore post vel ante fixam quandam stellam sol quotidie ad meridianum perveniat.

Sic posset sciri an celeritates terrae sint in contraria ratione distantiarum à sole, an in contrariae subduplicata.

Quod si posterius in Terra obtinet, idem sine dubio et in reliquis planetis.

En marge: Vide observationes diametri solis Moutoni, Piccardi²⁹⁾.

Constituta theoria Solis sive Terrae, orbitae ☿ figura quaerenda observationibus maximarum digressionum à Sole.

On voit que suivant Huygens l'orbite de Mercure n'a pas encore été déterminée avec assez de précision, aussi peu que celle de la terre.

28) Manuscrit F, p. 8.

29) G. Mouton ‘Observationes Diametrorum Solis et Lunae apparentium’, 1670; voyez le titre complet à la p. 59 du T. XVIII. Consultez sur la mèthode d'observer d'Auzout et de Picard la note 2 de la p. 91 qui précède.

[p. 143]

§ 11³⁰⁾.

Forsan planeta minori tempore à perihelio ad aphelium pervenit quam ab hoc ad illud.

[Fig. 44]

Forsan hujusmodi est planetae orbita; arctior scilicet versus solem [Fig. 44]. Quo fiet ut, posita excentricitate terrae dimidia tantum ejus quae fuit veteribus, mora longior in hemispherio aphelij quam perihelij ea esse possit quae revera observatur etiamsi celeritas in perihelio ad celeritatem in aphelio ponatur in subdupla ratione distantiarum, quod omnino naturae conveniret.

Observationibus investigandus esset progressus Terrae diurnus circa aphelium et perihelium. Et distantiae a Sole ex observatis solis diametris colligendae, quod jam satis accurate praestitum a Moutono et Picardo²⁹⁾.

30) Manuscrit F, p. 8.

29) G. Mouton ‘Observationes Diametrorum Solis et Lunae apparentium’, 1670; voyez le titre complet à la p. 59 du T. XVIII. Consultez sur la mèthode d'observer d'Auzout et de Picard la note 2 de la p. 91 qui précède.

§ 12.

Note ajoutée plus tard (Man. F. p. 8): 14 Dec. 1688. Hasce omnes difficultates abstulit Clar. vir. Neutonus, simul cum vorticibus Cartesianis; docuitque planetas retineri in orbitis suis gravitatione versus solem. Et excentricos necessario fieri figurae Ellipticae. Valeat igitur et Wardi, Pagani et Bullialdi prima hypothesis.

Pour la machine Planetaire³¹⁾.

31) Nous empruntons ce titre à la p. 24 du Manuscrit F.

§ 13³²⁾.

AOC [Fig. 45] orbita planetae elliptica, puta Mercurij, quae huic prorsus similis est secundum Keplerum, atque omnium maxime a circulo recedit. Focus alter E. Sit ABC circulus circumscriptus centrum habens D. Et oporteat ex anomalia media invenire coequatam. Id hoc modo proxime assequemur. Sit arcus CH aequalis anomaliae mediae datae. - En marge: Vide an simile quid invenerit Bonaventura Cavallerius apud Ricciolum³³⁾. - Et ex foco ubi sol ponitur, jungatur EH, et huic

32) Feuille collée sur la p. 23 du Manuscrit. Voyez sur ce § et le suivant les p. 125 et suiv. de l'Avertissement,

33) Huygens fait allusion au Scholium III (p. 535) à la Prop. 3 ‘Planetae iter est per lineam Ooidem id est Ouiformem, seu Ellipticam; seu Orbis illum deferens non est perfectus circulus, sed Ellipsis’ du Caput V ‘De Hypothesi Kepleri, & Bullialdi’ de la Sectio Secunda ‘De motu longitudinis Saturni Iovis et Martis ejusque Theorica, & Hypotheseos Fundamentis’ du Liber Septimus ‘De quinque Planetis minoribus’ (les deux autres étant suivant l'auteur, comme suivant les anciens, le soleil et la lune) de la Pars Prior Tomi Primi (Bononiae, ex typ. haer. V. Benatij MDCLI) de l'‘Almagestum Novum, astronomiam veterem novamque complectens etc.’, auctore P. Ioanne Baptista Ricciolo Societatis Iesu Ferrariensi, Philosophiae, Theologiae & Astronomiae professore.
Riccioli y cite le ‘Directorium generale uranometricum’ de 1632 de B. Cavalieri, ouvrage que Huygens connaissait d'ailleurs aussi lui-même (voyez la p. 202 de notre T. XX).
Dans le passage en question Cavalieri tire en effet (pour employer les lettres de notre Fig. 45) la droite DK parallèle à EH, CH étant l'‘anomalia media’ donnée, et observe, comme Huygens le fait ici, que l'espace EKC est à peu près égal au secteur DHC. Ensuite il raisonne différemment.

[p. 144]

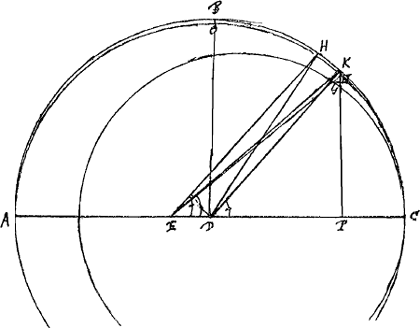[Fig. 45]

parallela agatur DK, ac jungatur EK. Erit jam arcus KC anomalia excentri proximè. Nam quia DK parallela est EH, erit triang. DEH aequale triangulo DHK quod insensibiliter differt a sectore DHK, arcui HK insistente. Quare addito utrinque sectore DKC, fit spatium EKC aequale proximè sectori DHC, ideoque arcus KC proxime anomalia excentri conveniens anomaliae mediae HC.

Angulus autem KDC aequalis est angulo HEC qui habetur hoc modo, scilicet faciendo ut summa laterum ED, DH ad eorum differentiam, hoc est, ut EC ad EA, ita

[p. 145]

tangens ½ ang. HDC ad aliam quae est tangens ½ differentiae angulorum E et H in triangulo EDH. Proportio autem CE ad EA est constans ac data, cujus proinde logarithmum tantum opus est auferre a logarithmo tangentis ½ anguli HDC sive ½ anomaliae mediae, residuum erit tangens [lisez: logarithmus tangentis] ½ differentiae angulorum E et H, quae ½ differentia addita dimidiae summae, hoc est ½ angulo HDC, efficiet angulum HED, seu KDC. Jamque simili plane ratione invenietur hinc angulus E in triangulo KED, nempe auferendo dictum logarithmum rationis CE ad EA à logarithmo tangentis ½ ang. KDC. nam reliquum erit tangens ½ differentiae angulorum KED, EKD, quae ½ differentia addita ad ½ summam, hoc est ad ½ angulum KDC, dabit angulum KEC.

Non est autem KEC angulus anomaliae coequatae, sed ducta KP perpend. in AC, quae secet ellipsin in N, erit N locus planetae in orbita, ideoque angulus NEC anomalia coequata. Qui facile invenitur auferendo à logarithmo tangentis anguli KEC logarithmum rationis BD ad DO, quae constans est. Nam reliquum erit tangens [ou plutôt: logarithmus tangentis] anguli quaesiti NEC.

§ 14³⁴⁾.

LDE [Fig. 46] orbita planetae circularis. S sol. SA excentricitas. E aphelium.

[Fig. 46]

Anomalia media accipiatur arcus EP sive angulus PAE.

Jungatur SP cui parallela sit AT. Erit planeta in T. ductaque ST, angulus anomaliae coequatae TSE. Ducta TMN perpend. in LE, erit Keplero planeta in puncto ellipseos M.

Sit³⁵⁾ AL [Fig. 47] orbita planetae cujus centrum C. Sol S. In recta per SC fiat ut excentricitas SC ad radium CA ita CE, ad lubitum sumta, ad ED. quo radio, ac centro E describatur circulus DM. Intelligatur porro circulo AL super centro suo C mobili affixum esse immobiliter circulum DM, incisum dentibus aequalibus super circuli plano erectis, qui proinde circulus necessario quoque super centro C movebitur. Ponatur autem moveii versatione aequabili tympani KH axem ad C directum habentis cujusque dentes congruant dentibus rotae DM; satis enim conveniunt, etsi ob excentricitatem hujus rotae non semper tympano ad rectos angulos subjiciantur.

34) Manuscrit F, p. 19.

35) Manuscrit F, feuille collée sur la p. 22.

[p. 146]

Dico hoc motu planetam inaequaliter ferri in sua orbita idque ita ut exigit hypothesis nostra, Keplerianae proximè aequipollens.

[Fig. 47]

Ponatur ex. gr. arcus DO esse ⅛ circumferentiae centro E radio ED descriptae; ejusque arcus dentes transijsse versatione tympani HK, unde recta CO erit necessario in recta CAD, etsi non ita ut punctum O sit in D, sed interius in R, quod CD non sit aequalis CO, sed duobus CE, EO. Quantus igitur est angulus OCD, tantus quoque erit angulus quo recta CAD mota erit circa centrum C. ideoque si faciamus angulum DCT aequalem angulo OCD, erit CT recta in quam promota erit CAD. adeo ut planeta processerit ex A in punctum N, ubi recta CT secat circumferentiam AN centro C descriptam. Apparet autem ob eandem angulorum aequalitatem arcum DM quem recta CT abscindit in circumferentia ODM esse aequalem arcui DO. Unde junctâ ME erit et angulus MED aequalis DEO, ut proinde quoque 45 gr. Itaque si fiat arcus AL 45 gr. jungaturque CL, erit haec parallela EM. In triangulis igitur CEM, SCL erunt anguli aequales E et C. Sed et latera eorum circa hos angulos sunt proportionalia ex centro, nimirum CE ad EM, quae est aequalis ED, ut SC ad CL quae aequ. CA. Ergo etiam aequales anguli MCE, LSC, ac proinde latera CM, SL parallela. Ideoque N locus planetae debitus medio motui AL, secundum hypothesin nostram. Sed AL ∞ DO. unde &c.

Quod si tympanum quovis alio loco velut in P ponatur aeque distante à centro C versus quod tympanum dirigitur, collocetur vero punctum D, quod in rota ODM maxime a centro C distat, sub tympano, et planeta rursus in A, loco aphelij sui. apparet

[p. 147]

aequali versatione tympani in P atque in D, eosdem angulos transire circa centrum C. Quare ubicunque collocetur tympanum idem sequetur planetae motus, si quem admodum diximus planeta collocetur in aphelio cum D punctum rotae ODM maxime à centro C remotum, directe tympano suppositum est, dentes autem tympani ad C punctum dirigantur.

His constat ratio Machinae nostrae Planetariae. Sed cum in uno eodemque axe sint tympana omnia, non poterit ille nisi ad duorum planetarum centra debite collocari.

[Fig. 48]

AP³⁶⁾ orbita planetae [Fig. 48]. Ad dividendas orbitas inaequaliter sit C centrum orbitae, S sol, hoc est CS excentricitas. Centro S radio SD ∞ CA fiat circumferentia, quae in partes aequales dividatur. Et per divisionum puncta ducantur rectae ex C, hae facient in orbita AP partes inaequales quaesitas, quas nempe aequalibus temporibus planeta percurrit, sed positu contrario quam sunt reipsa: nempe in A maximas, in P minimas.

Utraque haec methodus eundem motum dat planetae, qui respondet hypothesi Cepleri tam prope ut invisibilis sit differentia etiamsi orbis Saturni bipedalis sit diametri.

Ponendo PSA [Fig. 49] esse ellipticam Kepleri orbitam, nostra methodus planetam

[Fig. 49]

36) Manuscrit F, p. 22.

[p. 148]

ponit in Q, cum Keplero est in R, facta QR perpendiculari ad AP. Sed ellipses tam parum a circulis recedunt ut non possit in machina animad verti differentia. Et fortasse nos propiores veritati.

Hic non est necesse ut tympani K axis exactè dirigatur versus C; quia etiamsi hoc non ita sit, tamen singuli dentes tympani transire cogunt totidem dentes inaequales orbitae AP, quoniam haec super centro suo C convertitur.

Ut rotis aequaliter divisis inaequalis motus planetae exhibeatur. sit PA orbita planetae, S sol, C centrum orbitae. unde SC excentricitas. Ut SC ad CA ita sit CE, pro arbitrio adsumta, ad ED. Et centro E radio ED fiat circumferentia RD, quae in partes aequales dividatur, et dentibus incidatur aequalibus, qui aptentur dentibus item aequalibus rotae GHLK. quae conversa motu aequabili, circumducat rotam RD mobilem circa centrum C, et affixam orbitae AP. Jam si planeta affigatur huic orbitae, ut sit in aphelio cum punctum D rotae ED est sub axe rotae GL, movebitur planeta motu aequabili qui requiritur.

§ 15³⁷⁾.

Distantiae planetarum a Sole in partibus quarum semidiameter orbitae telluris est 100000.

	Aphelia	Media, seu potius radius orbitae	Perihelia
♄	1005207	951000	896793
♃	544708	519650	494592
♂	166465	152350	138235
♁	101800	100000	98200
♀	72900	72400	71900
☿	46655	38806	30657

Excentricitates in partibus qualium semidiametri cujusque orbitae 100000		Excentricitates in partibus qualium orbis magni [l'‘orbis magnus’ est l'orbite de la terre] semidiam. 100000 quae sunt differentiae mediarum et apheliarum, vel mediarum et periheliarum distantiarum.
	5700	54207	♄
	4822	25058	♃
	9263	14115	♂
	1800	1800	♁
	694	500	♀
	21000	8149	☿

37) Manuscrit F, p. 12. Les ‘distantiae planetarum’ et les ‘excentricitates’ sont empruntées aux p. 732 et 764 de l'‘Epitome’ de Kepler.

[p. 149]

Aphelia et Nodi ad annum 1681 completum. hoc est ad 1 Jan. 1682. St. Jul.³⁸⁾.

^{39)40)41)42)43)}

38) Ce tableau est emprunté aux Tables Rudolphines de Kepler.

39) On voit ici que Huygens se base sur une table qui indique la longitude de l'apogée du soleil au lieu de donner celle de l'aphélie de la terre.

40) Le signe ☊ désigne le noeud ascendant.

41) On trouve en effet la longitude 5^o0′0″ de ♒ pour l'aphélie de Vénus (année 1640 ou plutôt fin de 1639) dans le Cap. XV et la longitude 13^o22′45″ de ♊ pour le noeud ascendant de la même planète (même année) dans le Cap. VIII de ‘Venus in Sole visa’ de J. Horrox, traité publié en 1662 par Hevelius conjointement avec son observation à lui ‘Mercurius in Sole visus Gedani’ (Gedani, S. Reininger).

42) Ici Huygens a pris par erreur de plume 25 au lieu de 24. Pour la longitude de l'aphélie de Saturne au 1 janvier 1682 il aurait donc dû écrire 26^o39′46″ ⇸. Cette erreur s'est perpétuée dans la ‘Descriptio’ du planétaire publiée en 1703.

43) Manuscrit F, feuille collée sur la p. 23.

[p. 150]

Anni⁴⁴⁾ tropici longitudo, sive periodus Telluris sub Ecliptica dierum 365 h. 5 min. 49′15″46‴. at sub fixis dierum 365. h. 6. 9′.26″.43½‴.

Periodus Mercurij sub Ecliptica dies 87 h. 23.14′24″

Veneris sub Ecliptica 224 17.44′55

Martis sub fixis ann. Aegypt. 1, diebus 321. h. 23.31′56″49‴ sive diebus 686.

Jovis sub fixis ann. Aegypt. 11, d. 317. 14 h. 49′31″56‴

Saturni sub fixis ann. Aeg. 29, d. 174. 4 h. 58′.25″30‴

44) Manuscrit F, p. 14.

§ 16⁴⁵⁾.

ce qui conduit à la proportio revolutionum 105190 ⫟ 25335 [en douzièmes parties d'heure, voyez aussi le nombre 105190 à la p. 188 qui suit].

Développement de ce rapport en une fraction continue:

Si incipias in D, hoc est, si tantum 2 + 1/1 consideres, relictis coeteris deorsum, erit ergo D ∞ 3 unde C ∞ 1⅓ seu 4/3, B ∞ 1 + ¾ seu 7/4, A ∞ 6 + 4/7 seu 46/7. Ergo quotiens primus 4 + 7/46 seu 191/46. Unde numeri dentium 191 et 46.

Si incipias à C, fiunt numeri dentium 137 et 33.

Si incipias à B, fiunt numeri dentium 54 et 13.

Eligendi 137 et 33 vel potius 191 et 46.

Quo inferius incipies eo propiores verae proportioni fient numeri, nec possibile est sic inventis propiores ac simul minores reperire.

25335 - 105190 - 33 dentes minoris rotae / 137 1/68.

Tot dentes deberet habere rota major quae annuas conversiones facit. Ergo annis 68 uno dente promovenda. Simulque rota minor progreditur uno dente ex 33. hoc est gr. 10 min. 55. Ergo anno uno deficiet ☿ a loco è sole debito 9′.38″. En marge: cum rota annua habet dentes pauciores debito, sed tamen convenientes dentibus rotae Mercurij 33, sequitur inde ut conversione rotae annuae non tantum promoverit rota Mercurij quantum debuisset. Ergo promovenda.

45) Manuscrit F, p. 14-18.

[p. 151]

Quod si numeros dentium 83 et 20 retinuissem antehac inventos⁴⁶⁾, debuisset major habere 83 1/26. Unde annis 26 retroagenda uno dente, qui in minori rota habente 20 dentes efficiet gr. 18. Unde, annis singulis, 42′ excederet ☿ locum ex Sole debitum. hoc est plus quam quadruplum ejus quod fit adsumtis numeris 137 et 33.

Numeri dentium 13 et 8 vel 26 et 16.

Le nombre 13 1/681 correspond plus précisément à 8. Donc:

Singulis 681 annis uno dente promovendae rotae, qui dens facit 45 gr. in orbita ♀, unde annis singulis circiter 4′ deficit Veneris locus.

Martis. Periodus Terrae sub fixis 365. h. 6. 9′.26″. Periodus ♂ sub fixis 686. 23. 31′56″.

⁴⁷⁾

Numeri dentium 79 et 42. Plus précisément le rapport est 79:42 1/316.

Singulis 316 annis uno dente promovendae rotae, qui dens facit in orbita Martis 4^o.33′. Unde annis singulis fere 52″ deficit locus ♂.

Romeri 47 et 25. Si sumantur numeri Romeri 47 et 25, singulis 93 annis retroagendae rotae dente uno, qui in rota Martis facit 7^o.39½. Unde annis singulis locus Martis excedit verum ex sole fere 5 min.

Jovis. Periodus terrae sub fixis 365. 6 h. 9′.26″.

Ann. Egypt (365)

46) On voit à la p. 13 du Manuscrit F qu'avant de recourir aux fractions continues Huygens avait tâché de trouver des nombres approximatifs en considérant les logarithmes des termes du rapport.

47) En négligeant la dernière fraction écrite ¼, Huygens trouve successivement en remontant les fractions ⅖, 5/57, 37/42, 79/42. Auprès de la fraction ⅖ il nota: Sumsit Romerus pro [⅖] 2/6 sive ⅓. On voit que Huygens avait vu les calculs de Roemer. Celui-ci ne semble pas s'être servi de fractions continues. Voyez encore sur ce sujet la Pièce de la p. 97 du Manuscrit F intitulée ‘Avantages de ma machine par dessus celle de M. Romer’, qui a déjà été imprimée aux p. 377-378 de notre T. VIII: consultez la troisième ligne d'en bas de cette p. 377 et la note 4.

[p. 152]

Donc: Singulis 361 annis dens unus retroagendus qui in rota Jovis efficit 4^o20′. Unde singulis annis Jupiter excedet verum locum 43″. Una periodo 8′.30″ circiter.

Saturni. [Periodus terrae sub fixis] 365. 6 h. 9′.26″.

Ann. Egypt. (365)

Rotarum dentes 59 et 2 vel 118 et 4. Plus précisement: 59:2 1/339. Donc: In annis 339 unus dens promovendus, qui in rota ♄ facit 6^o.6′. Unde uno anno ferè 1′5″ deficit locus ♄.

☾ et ♁ 29 d. 12h. 44′ 365.5 h. 50′ ce qui conduit pour la lune et la terre au rapport 8505 - 105190 ou

ou à peu près 136:11 (plus précisément 136:11 - 1/256 ou 136 1/21: 11 ou plutôt 136 1/20¾: 11). Par conséquent, en prenant 136 et 11 pour les nombres des dents:

In annis 20¾ uno dente promovenda lunae orbita. qui facit 32 gr.

Plus bas: Dentes 235 et 19 multo praestarent. Huygens écrit encore: Ponendo ⅙ pro ultima fractione fiebant numeri 1546 et 125 quorum prior non habet partes aliquotas praeter 2 et 773. Ideo proximum sumsi 1/7 qui dat 1781 et 144. quorum prior fit ex 137 et 13.

Observation générale sur les calculs qui précèdent: Multo melius haec post folia 36. Comparez à la p. 163 qui suit, l'observation par laquelle se termine la présente Pièce.

Dentes rotae annuae

137.	☿	33.	In annis 68 uno dente promovendae hoc est in orbita ☿ gr. 10.55′. Ergo in anno deficit 9.′38″.
13.	♀	8.	vel 26.16. In annis 681 promovenda 45^o. In anno uno deficit 4′.
42.	♂	79.	In annis 316 promovenda 4^o33′. In anno deficiunt 52″.
7.	♃	83.	In annis 361 retroagenda 4^o20′. In anno excedet verum locum 43″.
4.	♄	118.	In annis 339 promovendus ♄ locus 6^o6′. In anno deficit 1′.5″.

[p. 153]

Duo circuitus in anno.	Unus circuitus in anno.
164-79. Annis 390 gr. 4½ prom.	191.	☿	46	In annis 104 uno dente retroagenda. hoc est fere 8 gr. in rota ☿.
13-16.	13.	♀	8	vel 52 et 32.
21-79.	42.	♂	79
11-261. In 12 annis 1′.40″ promov. in annis 599 uno dente.	29.	♃	344	Annis 1757 uno dente promovenda. hoc est 1^o.2′.47″.
6-12/11-324. In 30 annis 1′.30″ retroag. in annis 1338 uno dente.	11.	♄	324	Annis 1338 uno dente. hoc est fere 1^o.7′ retroagenda. hoc est periodo una fere 1′.30″. in anno 3″.
136-11	136.	☾	11	In annis 20¾ uno dente promovenda lunae orbita.

§ 17⁴⁸⁾.

Si aequales dentes facias,

Annulus super plano affigendus. Rotae axis annui in longitudinem extendendae. Annulus paulo altior in perihelio quam aphelio faciendus. In Mercurio necessario aequales dentes faciendi. In omnibus orbitis melius convenient sibi invicem dentes. Facilius dentes aequales elaborantur quam inaequales. Artificiosius videbitur aequales fecisse. Poterit circum affigi annulus, et rota tota superimponi orbitae.

Si inaequales dentes facias,

In Mercurio tamen aequales faciendi qui differet a caeteris. In omnibus orbitis minus exacte convenient quamsi aequales. Difficilius elimantur. Melius et facilius circum affigitur annulus. Facilius concentricae rotae ordinantur. Non opus extendere in longum rotas annuas. Divisio satis facilis, et ab organopoeo peragi potest.

La pièce⁴⁹⁾ de plaque AA [Fig. 50] entre ☿ se ♁ se doit mettre la derniere de toutes.

Moulure de cuivre autour de la plaque de devant, afin que la glace ne touche point aux planetes.

48) Manuscrit F, p. 23.

49) Manuscrit F, p. 21.

[p. 154]

§ 18⁵⁰⁾.

[Fig. 50]

Pour attacher un horloge, il faut faire un pignon de 5 dens, qui prenne la grande roue annuelle de 73 dents qui fait aller les jours. Et ce pignon doit saire un tour en 25 jours. Ainsi chaque dent du pignon passera en 5 jours, et en pareil temps chaque dent de la dite roue annuelle. Et ainsi elle fera un tour en 365 jours, parce que 5 fois 73 font 365.

Le pignon peut bien estre aussi de 6 dents et faire un tour en 30 jours. ou de 4 dents et tourner en 20 jours.

Le pignon A [Fig. 51] aura une queue creuse BCDE qui embrassera son axe et sera fixè sur cet axe par une vis F qui percera un costè de la queue. Et relachant la vis le pignon roulera sur son axe en sorte que, le pignon A tournant par le moyen de l'axe general des planetes lors qu'on le fera aller avec la main, l'axe du pignon A n'ira pourtant que lentement suivant le mouvement de l'horloge. Et par ce moyen les dents du pignon demeureront tousjours engrenees dans la roue annuelle de 73.

[Fig. 51]
* axe du pignon A, et non pas l'axe general

La vis F aura une queue assez longue pour venir a la circonference de la boete.

La pendule pourra estre d'environ 18½ pouces, pour faire 2 secondes en 3 vibrations. Ajouté plus tard: J'ay pris le balancier a ressort spirale pour plus grande commoditè. Comparez le § 21 qui suit.

Il y aura une roue horizontale annulaire ou plus tost perpendiculaire et platte d'environ un pouce et demi de diametre ou seront marquees autour les 12 heures, qui paroistront par une ouverture la moins grande qu'il se pourra entre les orbites de Jupiter et Mars.

50) Manuscrit F, p. 23.

[p. 155]

Le pendule fera un peu de bruit, il faut tascher d'y remedier. (En marge: il faut mettre des morceaux de drap sous les pieds de l'horloge contre la grande plaque). Les minutes et secondes auront de mesme leur ronds et trous pour paroistre. peut estre a costè l'un de l'autre.

Peut estre un volant pesant, dont le pignon de 6 dents engrenera dans la roue annuelle de 73; par ce moyen le mouvement des planetes sera plus egal et sans secousses, quand on tournera le grand axe.

§ 19⁵¹⁾.

Il faut bien applatir les deux plaques.

River les pieds, qui les tiendront ensemble, a la plaque de devant, apres avoir percè les placques l'une sur l'autre, et avoir fait les trous parfaitement correspondants l'un a l'autre.

Il faut avoir egard ou l'on placer[a] bien ces pieds devant que de faire leur trous. C'est a dire en sorte qu'on puisse commodement demonter et remonter la machine apres que la plaque de devant aura estè couppée en ses 7 parties.

Pour la remonter, il faudra placer et attacher ces 7 parties une à une, en commencant par l'exterieure et plus grande, et ainsi de suite. Et pour cela il faudra que les pieds de chaque partie soient ordonnez vers sa circonference interieure plustost que vers l'exterieur; parce qu'on y pourra regarder plus facilement pour les faire entrer dans leur trous. Toute fois les trous estant percez bien juste, comme il faut, il y pourra aussi avoir des pieds vers la circonference exterieure des pieces.

En remontant la machine il faudra placer la plaque de derriere perpendiculairement sur un costè, pour pouvoir serrer les pieds avec leur vis, quand ils seront passez.

Il faut achever tous les mouvements sans coupper encore la plaque de devant, ou du moins si on perce les orbites d'y laisser des endroits non percez, a fin qu'elle tiene toute ensemble. Mais il sera malaisè de faire entrer tous les pieds dans leur trous de la plaque de derriere. Et peut estre il sera mieux de coupper la plaque de devant, auparavant que de l'attacher sur l'autre. mais il faut que les pieds soient bien d'egale hauteur et la plaque de derriere bien droite.

Peut estre il seroit bon de la fortifier par quelques regles sur le champ.

Chaque orbite mobile doit estre retenue par sa circonference exterieure contre sa piece de la plaque de devant, et en demontant la machine elles y demeureront jointes. Il suffira que les orbites soient retenues en 4 endroits.

Le cercle des jours aura plus affaire de roulettes qu'aucun autre. Mercure, Venus et la Terre n'en auront point ni peut estre Mars.

51) Manuscrit F, p. 24-26.

[p. 156]

La roue D [Fig. 52] et le petit tuyau dans lequel tourne le bout de la manivelle M tiendront au costè de l'octogone. L'axe PT tiendra a la grande placque, et son bout P demeurera en dedans du costè de l'octogone comme aussi le bout H du grand arbre.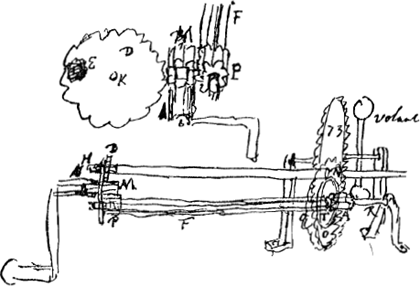

[Fig. 52]

Le pignon A qui engraine dans la roue 73 aura une plaque ronde attachée NO, et l'axe RP qui le traverse passera librement dans un tuyau depuis T jusqu'a P, ou est le costè de l'octogone ou l'on tourne le grand axe. Et ce tuyau en T, aura attachè une roüe platte dentee de l'horloge. En pressant fortement le tuyau du costè P, les deux ronds seront serrez l'un contre l'autre, et alors le pignon A estant agitè par l'horologe, entrainera la roue 73, avec tout le grand axe. de sorte qu'il faut effectuer cette pression du tuyau lors qu'on voudra laisser aller la machine d'elle mesme par l'horloge. Et quand on la voudra faire aller par la manivelle du grand axe, alors on relachera la dite pression, afin que la roue 73 tourne sans entrainer la roue platte de l'horologe, laquelle ira son chemin, mais seulement le pignon A.

Il seroit bon (en marge, s'appliquant à tout l'alinéa: Cecy auroit eu trop d'embaras) qu'en ouvrant le trou pour appliquer la manivelle a l'axe, cela fit en mesme temps relacher la pression du tuyau PT, et qu'elle revinst, lors qu'on rameneroit la petite coulisse qui ferme ledit trou. Pour cela, D sera une plaque ronde posée en dedans contre le costè de l'octogone de la boete. laquelle plaque aura un trou E, qui respondra au bout du grand arbre annuel. A costè de cette plaque, qui sera dentée autour, il y aura un trou rond dans le mesme costè de l'octogone, par ou l'on fera entrer le bout de la manivelle M, dentè autour, et ayant un creux quarrè en dedans, qui puisse prendre le bout du grand arbre lors qu'on appliquera la manivelle au trou E. La den-

[p. 157]

ture du bout M tournant dedans un petit tuyau percè de costè et d'autre engrainera d'un costè dans celle de la roue D, et de l'autre costè dans le pignon P, qui entre a vis sur l'axe PF, et lors qu'il tourne par le moyen de l'arbre dentè M, il serre le tuyau et sa roue dentée contre le rond NO, qui est attachè au pignon A. En mesme temps la roue D bouche le trou E. Et alors ayant tirè la manivelle M, l'horloge fait aller toute la machine par le moyen du pignon A, et le trou E se trouve fermè. Et pour le rouvrir, il faut remettre la manivelle M, et la tourner, ce qui fera en mesme temps desserrer le pignon a escroüe P, avec le tuyau PF, et le pignon A; de sorte que ce pignon tournera par le moyen de la roüe 73, lors qu'on agitera le grand arbre en appliquant la manivelle en H, et l'horloge ne laissera pas d'aller son train, faisant tourner lentement avec luy le tuyau PT par sa roue dentée attachee au bout T. afin qu'en remettant la manivelle en M, elle engraine dans la roue D et dans le pignon P, il faut faire les dents de ces deux minces vers l'entrée. Ainsi le pignon de la manivelle retrouvera les mesmes creux d'ou il estoit sorti en le retirant. En marge: non pas dans la dent de la roue qui aura serrè les plaques.

Pour diviser en parties egales les anneaux des orbites, il faut prendre une bande de papier qui fasse justement leur tour, et ayant estendu droit cette bande la diviser egalement selon le nombre de parties requis, et les marquer avec de l'encre. Puis coller la bande autour de l'anneau attachè sur l'orbite ou du moins fermè et a peu pres arrondi.

Pour diviser la bande en parties egales quand le nombre est premier, ou avec peu de parties aliquotes comme 191, 365, il faut calculer combien vaut une partie, en disant par ex. 191 donne 1, que donne la longueur de la bande prise sur l'eschelle, et ayant prise cette partie, ainsi trouuée, sur la mesme eschelle, on l'oste de toute la longueur de la bande. Le reste qui sont 190 parties on les divise en 10, puis chaque dixième en 19. Ou en adjoutant la valeur d'une partie, en sorte qu'il y en ait 192 on divise le tout en 6, puis les parties qui sont de 32 en 4, puis en 4 et puis en 2. On peut de mesme oster la valeur de 2, 3, 4, 5 ou plusieurs parties.

Devant que coupper la plaque de devant, il faut en faire une de mesme avec toutes les orbites et centres, et avec le grand arbre et ses roues marquees. afin de la garder pour modelle, pour quand il faudra faire de pareilles machines.

Plustost le costè de derriere; ou encore mieux a tous les deux costez.

Faire le cercle de l'ecliptique mobile, pour la precession des aequinoxes, car ce n'est que de cette precession que vient le mouvement des aphelies, qui a l'egard des fixes ne changent que tres peu ou point.

Marquer au dela de ce cercle des lignes vers spica virginis, prima arietis et autres grandes estoiles.

Voir ou mettre le grand arbre, en C ou en D [Fig. 53]. Resp. en C. En AB la charniere pour ouvrir toute la machine en la faisant sortir de sa boete. Au mesme endroit charniere pour la glace qui la couvre.

[p. 158]

En marge: J'ay trouvè meilleur d'attacher la machine dans la boete, et l'ouvrir par derriere.

[Fig. 53]

Pour eviter le bruit de la pendule, il faut la faire avec des petites vibrations a la maniere angloise.

Il valoit mieux de laisser entiere la partie de la plaque de devant qui contient les orbites de Mercure, Venus et la terre, pour y adjuster les roues dentees et les piliers, et puis les couper avec le compas tranchant.

La glace avec sa bordure s'appliquera par devant sans tenir avec une charniere, elle aura un anneau octogone plat d'un ½ pouce, qui entrera juste dans la boete octogone de bois, et sera attachè par une ou deux vis a teste platte dans les costez de dessus et dessous. On n'aura pas besoin d'oster cette glace que rarement, et elle est trop grande pour l'ouvrir a charniere. La forte placque appuiera dans la boete, et celle de devant sera tant soit peu moindre, afin de laisser entree a l'anneau de la bordure de la glace.

On pourra fortifier la boete avec du fer dans les angles. La boete appuiera sur une console belle et doree, ce qui soulagera la boete. Elle pourra estre de cuivre. Proportions des corps des planetes gravees par dehors.

Les pages 39-43 du Manuscrit F (comparez la note 55 qui suit) ont été publiées par nous aux p. 612-620 du T. XVIII. Il y est question de la forme des dents d'un pignon qui engrène dans une roue de champ à dents plates, ainsi que de celle des dents d'une roue de champ engrenant dans un pignon à dents plates. Comme on peut le voir dans le dit Tome, ces considérations de Huygens se rattachent à des considérations antérieures de Römer.

§ 20⁵²⁾.

En ostant la terre avec le cercle de la lune hors de son trou, l'on y pourra placer une Terre de cette grandeur [Fig. 54] et qui puisse tourner sur son axe, pour

[Fig. 54]

montrer les saisons et les jours et les nuicts. Il y faut graver le cercle equateur, et le meridien et le parallele de la France ou Hollande. En faisant un petit globe leger de bois ou autre matiere, et seulement la partie vers le pole austral, jusqu'au 23 degrè, de plomb, si avec cela la queue B est fort libre dans son trou: cette terre gardera tousjours son axe parallele a soy mesme, comme il faut. Et l'on pourra toutefois la tourner sur son axe, sans qu'elle retombe.

L'axe de la terre tiendra a la branche A et sera immobile, sur lequel la terre tournera. Note ajoutée plus tard: Elle sera d'argent et creuse.

Si l'on prenoit l'orbite de Saturne pour celuy de la Terre en cecy, il faudroit 30 tours de manivelle pour representer les saisons de l'annee au lieu qu'il n'en faudra qu'un seul.

52) Manuscrit F, p. 46-47.

[p. 159]

Petite plaque platte et ronde a l'endroit de nostre demeure sur la terrelle, pour representer le plan de l'horizon et le lever et coucher du soleil.

Avoir de mesme un Saturne avec l'anneau de cette grandeur [Fig. 55]. La queue sera attachee a une branche qui portera l'axe, comme a la Terre. L'anneau tiendra

[Fig. 55]

au globe et par le petit poids attachè au tuyau K, l'axe de Saturne et de l'anneau demeurera parallele a luy mesme. l'Axe doit estre inclinè sur le plan de l'ecliptique de 31 degrez.

Note ajoutée plus tard: Saturne et son anneau d'argent, la plaque ronde autour de luy qui porte ses 3 satellites de cuivre. Faire incliner Saturne et l'anneau de 31 degrez. L'axe de la plaque ronde de Saturne aura un poids perpendiculaire attachè qui tiendra cet axe tousjours parallele a soy mesme.

Peut estre sans serrer ou lacher la roue N [Fig. 56⁵³⁾] par le moyen d'une plaque, qui demande beaucoup de façon, il vaudra mieux de faire seulement un tuyau a cette roue N qui serre un peu sur l'arbre FH. Il faudra un peu plus

[Fig. 56]

53) Les petites figures à gauche représentent Saturne et Jupiter avec leurs satellites. Ici Jupiter en a quatre et Saturne trois. Un quatrième et un cinquième satellite de Saturne furent découverrs en 1684; voyez la p. 194 qui suit.

[p. 160]

que le double de la force qu'il faudroit autrement, a tourner la manivelle, car si je repousse une dent du pignon B, avec autant de force qu'il faudroit contre une dent de la roue A, pour faire tourner les planetes, il faut que la roue N avec son tuyau serre assez pour retenir l'arbre FH, au quel le pignon B est attachè, contre la dite pression de la dent de ce pignon; parce qu'autrement il paroit que la roue N agitée par l'horloge ne pourroit pas entrainer l'arbre FH assez fort pour que le pignon B, attachè a cet arbre, fist aller la roue A. Donc aussi en tournant la roue A par le moien de la manivelle en M, la peine de faire tourner l'arbre FH dans le tuyau de la roue N, sera un peu plus grande que si la dent de la roue A estoit retenue par une force egale a celle qu'il faut contre cette dent pour faire tourner les planetes. De sorte qu'en faisant aussi tourner les planetes, la force devra estre double et un peu plus, que si l'arbre FH tournoit sans empeschement ou frottement. Notez qu'en aggrandissant le pignon B l'on ne gagne rien. L'arbre FG pourra estre court par ce moyen. Il faudra voir si la force a la manivelle sera grande devant l'application de l'horloge.

On peut faciliter le mouvement de la manivelle en la mettant a l'arbre d'un pignon qui engraine dans une roue double attachée au grand axe, et faisant deux tours de manivelle pour une annee. Cela feroit venir le trou de la manivelle au milieu du costè ou comme on voudroit, et ce petit axe ne seroit plus de biais.

En marge: Notez qu'a quelque endroit difficile le tuyau courreroit risque de glisser. Mais on pourra faire une vis qui estant serree attache le tuyau de la roue N au grand arbre, et que l'on lachera quand on voudra tourner la manivelle.

A est la roue de 73 dents qui fait aller le cercle des jours. Elle engraine dans le pignon B attachè ferme sur l'axe FG aussi bien que le volant EE. Une plaque pareille D tient au tuyau F4 enfilè sur l'arbre FH qui est quarrè en cet endroit. En tournant la plaque ronde en M pour decouvrir le bout de l'arbre ML on trouvera moyen de serrer une plaque contre la roue N, libre autrement. Et alors l'horloge fera aller la roue A et partant tout le mouvement planetaire. Mais en relachant la roue N, du mesme mouvement qui referme le trou en M, l'on fera tourner la roue A par le moyen du grand arbre LM, et elle fera tourner l'arbre HF avec le volant EE, sans que cela fasse rien a l'horloge, qui ne laissera pas d'aller son train.

La roue N entre par son costè dans l'horloge, et engraine là dans un pignon dont l'axe est couchè horizontalement. En marge: vis sans fin dans l'horloge prenant dans la roue N.

§ 21⁵⁴⁾.

Il vaudra mieux de faire cette horloge avec un balancier a ressort spirale pour avoir moins d'embaras en l'ouvrant. Car aussi bien il ne s'agit pas d'une grande

54) Manuscrit F, p. 46-47.

[p. 161]

exactitude pour ce qui est des heures. Faire les temps du balancier en sorte qu'on puisse toujours appliquer un pendule de 18 pouces.

Suspendre le balancier par un fil de soye mais en sorte que les deux pivots ne puissent sortir de leur trous lors qu'on voudra coucher la machine. Le fil 3 ou 4 fois plus long qu'il n'est representè icy [Fig. 57]. Un petit contrepoids B qui soit egal a la pesanteur du balancier.

[Fig. 57]
Fils de soye au soleil et à la terre.

En faisant ce balancier grand, j'auray un essay de la justesse de ces horloges a ressort spirale⁵⁵⁾.

§ 22⁵⁶⁾. Le pignon B ayant 4 dents doit tourner en 20 jours. Ainsi a chaque 5 jours passera une dent de la roue A 73.

Grand trou dans la plaque de derriere, par lequel puisse passer la platine ronde ou sont gravees les heures.

Proportions des corps des planetes au Soleil se pourront placer entre Mars et Jupiter vers en bas. ou plustost sur une des plaques a costè sur la boete.

Quelques fixes marquees de celles qui sont pres de l'Ecliptique comme l'Epi de la Vierge. Seulement des lignes droites qui y tendent et marquent leur latitude.

Marquer le point ou les cercles dentez sont le plus distants des centres des orbites. Car lors que ce point est sous le grand axe alors la planete doit estre fixee a l'endroit de son aphelie. Puis pour trouver son lieu on cherchera par les tables Rudolphines le jour de son opposition avec le soleil.

Et ayant defait la vis qui tient le pignon au grand axe, on tournera le point fixe de la planete a ce lieu d'opposition, et alors on serrera derechef le pignon au grand axe par sa vis. Ainsi l'on placera separement chacune des planetes.

55) Les deux derniers alinéas ont déjà été cités à la p. 508 du T. XVIII; nous y avons reproduit aussi la présente Fig. 57.

56) Manuscrit F, p. 47-48.

[p. 162]

Peut estre les trous des jours et des annees [Fig. 58] vers en haut [Fig. 58 bis] entre ♃ et ♄ de les avoir pres du trou des heures. Ou les mettre tous trois vers

[Fig. 58]

[Fig. 58 bis]

en bas. Mais alors on ne peut adjouter de pendule. Entre Jupiter et Saturne vers en bas, l'on mettra la proportion des planetes entre elles et au soleil. Les corps des planetes gravez pour exprimer des globes. Autour du soleil graver des rayons partants du centre, pour faire paroistre son corps [Fig. 59].

[Fig. 59]

La glace un peu distante de la plaque afin que la petite terre postiche et le Saturne puisse estre enfermez dessous. Il faut voir si cela n'oste pas trop le jour a l'ecliptique.

On peut faire ouvrir tout l'ouvrage pour voir le dedans en attachant des pieces coudees a la plaque forte de derriere qui fassent la charniere a costè de la plaque de devant. ou seulement une pièce large. Il faudra un peu rogner la plaque de derriere du costè qui ouvre, parce qu'autrement elle ne pourroit pas entrer. La glace sera a la mesme charniere comme aux montres de poche.

Console dessous [Fig. 60] ou un pied jusqu'a terre. Il faudra y attacher la boete

[Fig. 60]

avec des vis. et l'attacher de plus a la muraille par en haut, a sin que si la console manquoit la machine ne tombe point.

Sur la plaque de derriere sera gravè combien en cent ans les places des planetes surpassent ou manquent des veritables, selon quoy l'on pourra les redresser.

Corpora solis et planetarum multo majora exhibentur quam proportione horum orbium esse deberent, quippe invisibilia alioqui futura. Uti et circulus lunae quo circa terram defertur. qui circulus diametrum fere duplo minorem habet quam sit diameter solis. Sunt enim a Terra ad Solem diametri terrae circiter duodecies mille, a terra ad lunam diametri terrae triginta. cujus distantiae duplum diameter nimirum lunaris orbis erit, circiter 4/7 diametri solis. Sunt autem proportiones omnium planetarum inter se atque ad solem quales hic expressae cernuntur.

[p. 163]

Vide post folia 34 quae ad emendationem hujus automati spectant⁵⁷⁾.

En février 1682 Huygens écrit à J. Gallois (T. VIII, p. 342): J'avois emporté avec moy, en quittant Paris, la machine Planetaire que monseigneur Colbert avoit agreé que je sisse construire, et qui n'estoit que commencée. Dans sa lettre à Colbert du 27 août de la même année il dit que le prix de la machine, telle qu'elle avait été construite à la Haye, est de 620 escus, dont il y en a 520 pour le compte de l'horloger [van Ceulen], et le reste pour ce que j'y ay deboursè icy et a Paris.

57) Consultez l'Avertissement suivant.