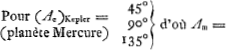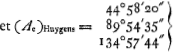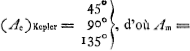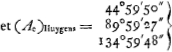Logo DBNL
Oeuvres complètes. Tome XXI. Cosmologie (1944)

Oeuvres complètes. Tome XXI. Cosmologie

(1944)–Christiaan Huygens–rechtenstatus Auteursrecht onbekend

Vorige Volgende

Projet de 1680-1681, partiellement exécuté à Paris, d'un planétaire tenant compte de la variation des vitesses des planètes dans leurs orbites supposées elliptiques ou circulaires, et considération de diverses hypothèses sur cette variation.

Avertissement.

Le planétaire que Huygens fit construire à la Haye en 1682 a été conservé jufqu'à nos jours et se trouve actuellement à Leiden au ‘Nederlandsch Historisch Natuurwetenschappelijk Museum’. La description de ce planétaire, telle qu'elle fut publiée en 1703 dans les ‘Opuscula postuma’1), date de beaucoup plus tard. Il est vrai qu'une description succincte se trouve déjà dans la lettre, non expédiée, du 6 février 1683 à S. Alberghetti2) dont les termes s'accordent avec une partie de la ‘Descriptio’ des ‘Opuscula postuma’; mais dans cette lettre Huygens ajoute: ‘Constitui vero ampliorem automati descriptionem posthac concinnare ac typis edere’.

En renseignant Colbert dans sa lettre du 27 août 16823) sur le planétaire récemment achevé - nous observons en passant que la pièce qui s'y rattache ‘Avantages de ma machine par dessus celle de Mr. Romer’ fait bien voir la concurrence avec l'astronome danois que nous avons constatée aussi dans les Pièces précédentes du présent Tome -, Huygens avait également écrit: ‘J'ai commencé une autre description plus ample’.

Mais même en 1690 il n'avait pas encore mis son projet à exécution, puisque dans le sommaire de sa lettre à de la Hire du 30 mars de cette année4) nous lisons: ‘Je

prepareray la miene [description] des Planetes5)’. Dans le présent Tome nous croyons donc, par respect pour la chronologie, devoir publier cette Pièce beaucoup plus loin.

Entre 1682 et 1690, grâce aux ‘Principia’ de 1687 de Newton, les idées de Huygens sur le mouvement des planètes avaient évolué. Il avait reconnu qu'une force inversement proportionnelle au carré de la distance au soleil peut être censée retenir les planètes dans leurs orbites et qu'il en résulte que c'est bien la variation de la vitesse telle que l'enseignait Kepler, premier auteur de la théorie des ellipses, du moins pour les planètes - car pour les comètes Kepler admettait le mouvement rectiligne6) - qui est la bonne.

En même temps, nous le disons plus amplement dans l'Avertissement au ‘Discours de la Cause de la Pesanteur’ de 1690, les idées de Huygens sur les tourbillons s'étaient modifiées. En 1680-1681, malgré quelques héfitations7), il croyait, pour les planètes circulant autour du soleil, au ‘vortex deferens’ de Descartes8), sans toutefois comprendre - est-il besoin de le dire? - comment ce vortex solaire peut faire tourner les planètes dans des orbites elliptiques ou dans des cercles excentriques ni pourquoi leurs vitesses varient dans ces orbites ainsi que l'observation le fait voir.

 

Avant Newton, il n'était certes pas déraisonnable - c'est le cas de Boulliau et de Ward - d'accepter la première loi de Kepler d'après laquelle les planètes se meuvent dans des ellipses dont le soleil occupe un foyer, ainsi que la troisième qui établit la proportionnalité des deuxièmes puissances de leurs périodes avec les troifièmes puissances des grands axes de leurs orbites, mais de douter de la deuxième suivant laquelle pour une planète quelconque les aires, en d'autres termes les secteurs, compris chacun

entre un arc d'ellipse et deux rayons vecteurs émanant du soleil, sont precisément proportionnelles aux temps que met la planète à parcourir ces arcs.

Il était également permis - c'est le cas de Huygens, comme nous le ferons voir -, de n'accepter que la troisième loi (voyez sur la troisième loi la p. 36 qui précède) et de douter de la vérité des deux premières.

Comme les excentricités des orbites elliptiques - en supposant qu'elles soient vraiment elliptiques - sont petites, Huygens n'avait certes pas de raisons suffisantes pour faire parcourir effectivement des ellipses par les planètes de son planétaire; on n'aurait guère pu les distinguer de circonférences de cercle, et il était donc bien plus simple de s'en tenir à ces dernières. Mais les variations de vitesse, différentes pour chaque planète, ne pouvaient être négligées, et la question se posait s'il fallait faire varier les vitesses, pour autant que le permettait la substitution des circonférences de cercle aux ellipses, suivant la loi de Kepler ou bien suivant une autre. D'ailleurs cette question astronomique des vitesses l'intéressait en elle-même. En février 16829) il écrit à de la Hire que ‘depuis peu’ il a ‘estudiè d'avantage en Astronomie que par le passè a l'occasion de la machine planetaire’.

Suivant Boulliau la forme elliptique de l'orbite avait été établie par Kepler pour la planète Mars. Il est d'avis que dans le temps où il écrit la forme elliptique doit être considérée comme également démontrée (ou plus ou moins démontrée), par les observations pour Mercure qui possède la plus grande excentricité10). Quant à la variation des vitesses, il substitue à la deuxième loi de Kepler une autre hypothèse qui fut également adoptée à son exemple par Seth Ward et de Pagan. C'est celle-ci, outre la loi ou hypothèse de Kepler, que Huygens considère en premier lieu dans la Pièce qui suit. Il y parle aussi brièvement d'une hypothèse de N. Mercator, et ses calculs font voir, ce qu'il indique d'ailleurs explicitement en quelques mots, qu'il a conçu lui-même une autre hypothèse qu'il dit pouvoir être plus exacte que celle de Kepler. Il est fort

possible qu'il ait développé cette hypothèse dans quelques feuilles séparées qu'il n'a pas jugé nécessaire de conserver. Nous tâcherons ici d'y suppléer de notre mieux.

Dans la lettre déjà citée à Colbert Huygens dit que ‘pour l'inegalitè’ il a ‘representè l'hypothese de Kepler’: il est évident qu'après l'oeuvre de l'astronome allemand aucune hypothèse ne pouvait paraître plausible qui ne conduisait pas à une variation des vitesses différant peu de celle que donne la loi des aires. On ne peut donc pas, nous semble-t-il, conclure de cette phrase qu'en août 1682 Huygens était déjà convaincu de l'exactitude absolue de cette loi dont la sienne ne s'écarte que faiblement. Dans sa lettre il n'entre pas dans les détails; il ne fait pas même mention du fait que dans la machine les ellipses de Kepler ont été remplacées par des circonférences de cercle, ce qui, comme nous le ferons voir, contribuait à rendre la différence entre l'hypothèse de Kepler et la sienne imperceptible et pratiquement nulle.

 

Hypothèse de Kepler. Acceptant la loi des aires, on peut se proposer, à l'instar de Kepler lui-même, d'exprimer par une équation comment varie avec le temps ce qu'on appelle aujourd'hui l'anomalie vraie, c.à.d. l'angle que fait avec le grand axe de l'ellipse le rayon vecteur qui joint à la planète le soleil, situé en un foyer. A cet effet, on peut considérer en même temps l'angle correspondant que fait avec le grand axe un rayon vecteur partant d'un point arbitrairement choisi sur cet axe11) et joignant ce point à une planète fictive parcourant uniformément dans le même temps que la planète réelle, non pas une ellipse, mais une circonférence de cercle (il s'agit, peut-on dire, d'une aiguille parcourant le cadran d'une horloge); cet angle est l'‘anomalie moyenne’. En 1769. J.L. Lagrange est parvenu à exprimer par une série convergente l'anomalie vraie en fonction de l'excentricité12) de l'ellipse et de l'anomalie moyenne13). Au dix-septième siècle il fallait encore procéder ‘tentando’. En consultant l'‘Epitome Astronomiae Copernicanae14)’ on voit que Kepler considère trois

anomalies différentes: l'‘anomalia media’, l'‘anomalia eccentri’ et l'‘anomalia coaequata’15). Cette dernière n'est autre que l'anomalie vraie. On peut dire que son ‘anomalia media’ est identique avec l'anomalie moyenne. Il en donne, il est vrai, la définition suivante16): ‘Quid est Anomalia media? Est spacium temporis, quod planeta consumit in quolibet arcu suae orbitae, ab apside incepto, redactum in partes - degrés - & minuta, qualium anomalia tota valet Gr. 360. numerationis logisticae vel Astronomicae’; mais les termes mêmes de cette définition font prévoir que dans les figures il ne s'agira pas d'un ‘spacium temporis’ mais d'un angle (ou d'un secteur de cercle): il n'est question de ‘spacium temporis’ que pour faire voir que cet angle croît uniformément. Quant à l'‘anomalia eccentri’ - ‘anomalia excentri’ ou ‘anomalia excentrica’ chez Huygens - c'est l'angle que fait avec le grand axe de l'ellipse un rayon, égal à la moitié de cet axe, émanant du centre de l'ellipse et dont l'autre extrémité se trouve à chaque instant avec la planète sur une même perpendiculaire au dit axe. On la désigne encore aujourd'hui par l'expression ‘anomalie excentrique’ quoiqu'il s'agisse à la vérité d'un angle que, pour éviter les confusions, on devrait plutôt nommer centrique.

Cette ‘anomalia eccentri’ est introduite pour calculer en deux étapes, ce qui semblait ne pas pouvoir être fait directement, l'‘anomalia coequata’ en fonction (pour employer ce terme) de l'‘anomalia media’.

La considération de la figure et la loi des aires conduisent aux équations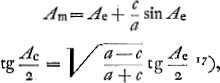



illustratie

17),

où a désigne la moitié du grand axe de l'ellipse, c son excentricité linéaire18), Ac, Ae et Am respectivement l'‘anomalia coequata’, l'‘anomalia excentrica’ et l'‘ano-

malia media’. La première équation est une équation du mouvement; la deuxième n'est autre chose, peut-on dire, que l'équation de l'ellipse pour les deux variables Ac et Ae. C'est la première équation qui ne peut être résolue que ‘tentando’; mais une fois qu'on a trouvé Ae pour une valeur donnée de Am on peut directement calculer Ac à l'aide de la deuxième formule.

Dans ces formules nous avons pris l'unité moderne pour les angles, et nous y considérons le sinus et la tangente l'un et l'autre comme un rapport de deux longueurs, non pas simplement, avec Kepler et ses contemporains, comme une longueur. Si l'on voulait exprimer Am et Ae en degrés, la première formule devrait s'écrire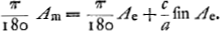



illustratie

En 1680, à une des dernières pages du Manuscrit E19), Huygens - c'est la première fois, semble-t-il, qu'il s'occupe de ce sujet - se pose le problème mathématique ‘data anomalia media et coequata invenire anomaliam excentricam’. Il est évident qu'il n'a pas en vue ici l'hypothèse de Kepler d'après laquelle il devrait se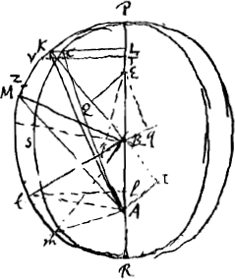

illustratie

proposer - première équation - de ‘data anomalia media invenire anomaliam excentricam’, et ensuite - deuxième équation - de ‘invenire anomaliam coequatam’.

 

Attendu que plus tard, en 1690 dans le Manuscrit G20), Huygens a bien rédigé, en acceptant l'hypothèse de Kepler, la solution de la première partie de ce dernier problème, énonce en entier sous la forme: ‘In Kepleri hypothesi ex anomalia media invenire anomaliam excentri et coequatam tentando’, nous avons cru devoir intercaler (§ 2) cette page de 1690. Il y dit à bon droit que Kepler est ‘longior et obscurus’. L'équation obtenue par Huygens (après Kepler): ‘Oportet igitur invenire arcum PK talem, ut addita ex parte proportionali sinus

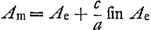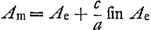sui KL secundum rationem BA ad BK vel BR, hoc est secundum rationem excentricitatis ad dimidium axem, summa fiat aequalis arcui anomaliae mediae datae’ correspond à l'équation illustratie, puisque les arcs PK et PM se trouvent sur une même circonférence de cercle et sont donc proportionnels aux angles Ae et Am. Huygens n'écrit pas la deuxième formule de Kepler, mais puisqu'il se proposait aussi de trouver l'‘anomaliam coequatam’ on voit que, connaissant Ae, il était apparemment en état de trouver Ac sans beaucoup de peine: en effet, lorsque l'arc PK est connu, la position du point C en découle et partant aussi l'angle CAP qui est l'‘anomalia coequata’ ou anomalie vraie Ac. Le calcul conduit à la formule générale. Dans les Manuscrits E21) et F22), en 1680-1681, Huygens énonçait21) - sans l'avoir démontrée, ce qu'évidemment il aurait pu faire - et résolvait à tâtons22) cette même équation illustratie: ‘Oportet invenire arcum PK qui additus ad ... etc.’ Et à la p. 6 du Manuscrit F il calculait numériquement une ‘anomalia excentri’ de la planète Mars d'après l'‘anomalia media’ donnée, en citant la p. 696 de l'‘Epitome’ de Kepler où il est en effet question de ce même calcul numérique: l'‘anomalia media’ donnée y est de 50o9′10″, d'où résulte l'‘anomalia excentri’ 47o42′17″.

 

Hypothèse de Boulliau et de Seth Ward. Dans son ‘Astronomia Philolaica’ de 1645, déjà citée plus haut, Boulliau propose sur la variation des vitesses des planètes dans leurs orbites elliptiques, dont le soleil occupe toujours un des foyers, une hypothèse qu'on trouvera énoncée par Huygens dans le § 3 qui suit. Malgré l'ellipticité de l'orbite et le manque d'uniformité du mouvement, Boulliau ne veut pas abandonner entièrement l'idée maîtresse des astronomes grecs n'admettant que les orbes circulaires et le mouvement uniforme. Il croit pouvoir combiner cette idée avec les observations modernes en plaçant l'ellipse sur un certain cône oblique à base circulaire dont une génératrice parcourt la surface conique de telle manière que le point d'intersection de la génératrice avec la base se meut uniformément sur la circonférence de cercle. Un des foyers de l'ellipse se trouve par hypothèse sur l'axe du cône - c'est

ainsi que le cône a été construit -, c.à.d. sur la droite qui joint le sommet au centre de la base. Le mouvement de la planète, suivant l'hypothèse de Boulliau, serait représenté par celui du point d'intersection de la génératrice considérée avec l'ellipse. Boulliau admire Kepler comme géomètre, mais il n'admet pas généralement - et qui voudrait le lui reprocher? - ses ‘causae physicae’: ‘Dolebam virum tam sagacem deserta Geometria ad Physicas causas transfugisse, transitu facto à luce ad tenebras’23). Mais ceci ne justifie guère son hypothèse à lui qui est à la vérité une hypothèse tout autre mais non pas plus essentiellement géométrique que la deuxième loi de Kepler; et l'on peut parler ici d'une idée préconçue de Boulliau, ce qui n'est pas le cas pour Kepler. Il est vrai qu'il nous est facile aujourd'hui de défendre ce dernier, sachant avec certitude qu'il avait raison. Pour les astronomes du dix-septième siècle, avant Newton, la chose devait être beaucoup moins claire.

En 1653 Seth Ward publia ses observations, en partie critiques, sur le livre de Boulliau24). Il démontre en premier lieu, ce que Huygens reproduit à sa manière dans notre § 3, que l'hypothèse nouvelle peut être énoncée plus brièvement et sans parler du tout du cône oblique: elle revient simplement à ceci que la planète se trouve constamment sur un rayon vecteur partant du deuxième foyer de l'ellipse - le premier étant celui occupé par le soleil - et tournant autour de lui d'un mouvement uniforme. Ward attire ensuite l'attention sur quelques erreurs mathématiques de Bouilliau. Ce qui fut également remarqué par Ward et est assurément plus grave c'est que Boulliau, voyant que les valeurs pour la planète Mars, calculées suivant son hypothèse, s'écartaient trop à son avis de celles de Kepler (ou de Tycho Brahé) leur avait tacitement substitué des valeurs tirées des ‘Tabulae Rudolphinae’ de Kepler lui-même que ses nouvelles tables, les ‘Tabulae Philolaicae’, devaient, aux yeux des lecteurs, avoir la prétention de corriger au moyen de la nouvelle hypothèse25).

Nous observons que Huygens qui connaissait les Tables de Bouilliau depuis longtemps26) - consultez notamment la note 9 de la p. 523 du T. XV - disait en 1666 ou 1667 à l'Académie que malgré la construction de ces Tables ‘l'on trouue qu'en general les Rudolphines sont celles qui approchent le plus du Ciel27)’.

Malgré tout, dans un ouvrage ultérieur de 165628), dédié à Neile, Hevelius, Gassendi († 1655), Riccioli et Boulliau, Ward croit devoir adopter l'hypothèse de ce dernier: ‘Ellipseos, cùm focus alter sit sol, super alterum interim focum, ita temperatur planetae cujusque motus, ut temporibus aequalibus, aequales illic angulos absolvat29)’.

Avant d'avoir pu prendre connaissance de ce dernier ouvrage, Boulliau avait composé la brochure qui parut en 1657: ‘Ismaelis Bullialdi Astronomiae Philolaicae Fundamenta clarius explicata & asserta adversus Clarissimi Viri Sethi Wardi Oxoniensis Professoris impugnationem30)’. Il y maintient, si l'on veut, son hypothèse, mais en la modifiant31). La planète ne se trouve pas précisément, pense-t-il maintenant, à l'intersection I de l'ellipse et du rayon vecteur tournant uniformément autour du deuxième foyer; pour obtenir la bonne position il faut mener par I une parallèle au petit axe de l'ellipse et joindre au deuxième foyer par une droite d le point où cette parallèle coupe l'ellipse. La planète se trouvera au point où l'ellipse est coupée par la droite d.

Huygens fait mention au § 3 qui suit de cette nouvelle hypothèse ou ‘limitatio’ de Boulliau. Ce qu'il désigne par hypothèse de Boulliau et de Ward, laquelle il appelle d'ailleurs généralement celle de Ward, c'est toutefois l'hypothèse non modifiée telle qu'elle fut interprétée et adoptée par l'astronome anglais. Mais la discussion entre les deux astronomes peut avoir donné à Huygens la conviction - voyez ses paroles à l'Académie citées plus haut - que si les tables de Kepler n'étaient apparemment pas tout-à-fait correctes - même endroit -, l'hypothèse de Boulliau ne l'était sûrement pas non plus.

Hypothèse de N. Mercator32). Ce savant que Huygens appréciait fort comme mathématicien - voyez notre T. XX sur Mercator et les logarithmes - avait débuté dès 1651 par des ouvrages astronomiques dont les premiers parurent en Allemagne. En 1664 il publia une brochure33) où il développe lui aussi une nouvelle hypothèse; c'est celle que Huygens examine dans le § 9 qui suit, en citant un ouvrage ultérieur du même auteur34). L'hypothèse qui n'a pas eu d'influence marquée sur Huygens revient à ceci. Qu'on divise la distance EA, qui sépare les deux foyers de l'ellipse, en moyenne et extrême raison35) de sorte que ED : DA = DA : EA, le soleil se trouvant

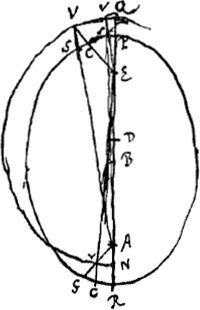illustratie

en A. Qu'on décrive ensuite une circonférence de cercle de rayon a (moitié du grand axe) non pas du centre de l'ellipse B, mais du point D. Puisse le rayon vecteur EV (le point V se trouvant sur la circonférence de cercle) tourner uniformément autour du foyer E. La planète sera alors par hypothèse à chaque instant en S, point d'intersection de la droite VA avec l'ellipse. L'angle PEV est son ‘anomalia media’. Huygens ne considère cette hypothèse que pour calculer le rapport qui en découle des vitesses de la planète aux apsides (périhélie et aphélie) P et R.

 

Suivant Kepler (deuxième loi) - et aussi suivant Ward - le rapport de ces deux vitesses est inversement proportionnel aux distances du soleil r1 ou a + c et r2 ou a - c. Donc v1 : v2 = 1/r1 : 1/r2. Mais comment concilier la

valeur de ce rapport avec la théorie du vortex solaire? Suivant la troisième loi de Kepler on a pour deux planètes différentes, dans l'hypothèse d'orbites circulaires, v1 : v2 = 1/√r1 : 1/√r2, et si le tourbillon est un ‘vortex deferens’, c.à.d. un tourbillon dont la vitesse égale en chaque endroit celle de la planète qu'il charrie, comme l'admet Huygens, cette dernière équation doit être valable pour les vitesses linéaires de la rotation de la subtile matière du vortex lui-même, ce qui est possible, quoique Huygens avoue ne pas savoir quelle est la cause intrinsèque de la diminution des vitesses suivant cette loi36). Mais s'il en est ainsi, comment expliquer que, dans le cas d'une orbite elliptique, les vitesses de la planète aux apsides obéissent apparemment à une autre loi?

L'hypothèse de Mercator donne-t-elle peut-être pour le rapport des vitesses aux apsides une valeur qui se rapproche tant soit peu davantage de la valeur 1/√r1 : 1/√r2? Le calcul37) fait voir que le contraire est vrai. Il ne reste à Huygens qu'à exprimer son étonnement: ‘Mirum in his hypothesibus qui possit materia vorticis conferre motum planetae perihelio, suo ipsius motu celeriorem’.

 

Hypothèse de Huygens. La p. 4 du Manuscrit F, ainsi que d'autres, est remplie de calculs numériques. On y lit e.a. (d'après la figure il s'agit de l'‘anomalia excentri’ et le calcul se rapporte à la planète Mercure pour laquelle le rapport c/a de l'excentricité au demi grand axe est 21/100)

  37.37.59 angulus KBP mihi  
  37.46. 038) angulus KBP Keplero.
Anomalia coequata mihi 31.20. 0   Wardo 30.15.58
  Keplero 30.48. 2   Keplero 30.48. 2
  _____   _____
  mea excedit 0.31.58   Wardi deficit 0.32. 4

Toutes ces valeurs correspondent à une ‘anomalia media’ de 45o.

Apparemment Huygens n'est d'accord ni avec Kepler ni avec Ward.

A la p. 5 on lit e.a.  
  37.4638) arcus PK sec. hyp. Kepleri 37o38′ arcus PK mihi
  37. 0 arcus PK sec. hyp. Wardi 8′ differo a Keplero
  _____  
  46′ differentia arcuum PK hoc est secundum viam
eam quam in automato secutus sum.  

Le lecteur pourrait être tenté d'admettre que cela ne signifie pas que Huygens a en vue une hypothèse théorique différant de celle de Kepler, mais seulement que dans la construction pratique de l'automate il a été obligé de s'écarter un peu de cette dernière. Cette opinion est pourtant insoutenable, puisque sur une feuille collée sur la p. 22 du Manuscrit (§ 14 qui suit) il écrit: ‘Dico hoc motu planetam inaequaliter ferri in sua orbita ita ut exigit hypothesis nostra, Keplerianae proximè aequipollens’ et encore ‘Ideoque N locus planetae debitus medio motui AL, secundum hypothesin nostram’, et qu'à la p. 22 il ajoute, après avoir dit que la différence entre Kepler et lui-même est imperceptible: ‘Et fortasse nos propiores veritati’.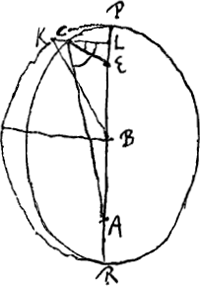



illustratie

Il faut donc bien prendre cette divergence au sérieux et examiner en quoi elle consiste.

Or, à la p. 4 déjà citée la valeur 37o37′59″ de Huygens de l'‘angulus KBP’ est obtenue par l'addition des angles 22o30′0″ et 15o7′59″, dont le premier est la moitié de 45o, c.à.d. de la grandeur qu'a par hypothèse l'angle PEC, où P est l'aphélie, E le foyer que le soleil n'occupe pas et C la planète. L'angle PEC est donc l'‘anomalia media’ suivant l'hypothèse de Ward. Quant à l'angle 15o7′59″, il est la moitié de l'angle 30o15′58″ représentant, comme nous l'avons dit plus haut, l'‘anomalia coequata’ de Ward; dans la figure c'est l'angle PAC.

Il paraît donc que suivant l'hypothèse de Huygens on a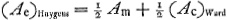

illustratie

Les formules (modernisées) de Kepler étaient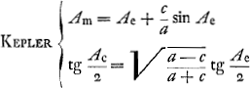



illustratie

Dans l'hypothèse de Ward ces équations doivent être remplacées par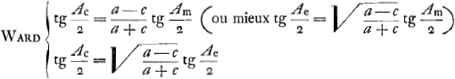



illustratie

La première forme de la première équation (équation du mouvement) est démontrée par Huygens au § 5 et exprimée dans les termes: ‘ut AP ad AR ita tang. ½ CEP ad tang. ½ CAP’. La deuxième équation est la même que chez Kepler puisqu'il s'agit de la même ellipse.

Dans le Manuscrit E, nous l'avons dit à la p. 116, Huygens se posait le problème: ‘data anomalia media et coequata invenire anomaliam excentricam’. Or, l'équation de Huygens que nous venons d'écrire, résout ce problème fort simplement, bien entendu en prenant pour l'‘anomalia coequata’ I'angle (Ac)Ward: l'‘anomalia excentrica’ de Huygens, suivant cette équation, est la moyenne arithmétique des deux autres. On voit que cette équation ne peut être dérivée ni des équations de Kepler, ni de celles de Ward. (Ae)Huygens, pour une même valeur de Am, diffère de (Ae)Ward tout aussi bien que de (Ae)Kepler. Voyez encore sur cette différence la note 39 de la p. 128 qui suit.

L'équation de Huygens, combinée avec la première équation de Ward, devient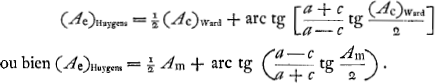



illustratie

Quant à l'‘anomalia coequata’ (31o20′0″) on voit à la p. 4 du Manuscrit F que dans un cas spécial elle est obtenue par l'addition de ½(Ae)Huygens et de arc tg 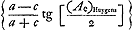illustratie. Les deux équations qui expriment l'hypothèse de Huygens peuvent donc s'écrire


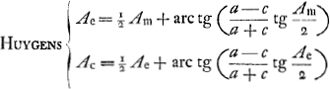illustratie

Comme dans le cas des hypothèses de Kepler et de Ward, la première de ces équations est une équation du mouvement de la planète, tandis que la deuxième est celle de la courbe dans laquelle elle se meut. Or, en introduisant, au lieu des variables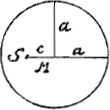

illustratie

Ac et Ae, des coördonnées cartésiennes, on constatera que cette courbe est une circonférence de cercle de rayon a où le soleil se trouve à une distance c du centre. En d'autres termes: la planète, suivant l'hypothèse de Huygens, parcourt, non pas une ellipse, mais un cercle excentrique. A la fin du présent Avertissement, nous faisons quelques remarques historiques à ce propos.

 

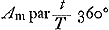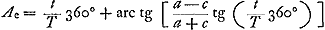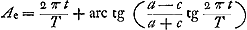Dans toutes équations on peut remplacer illustratie, où t est temps et T la période de la planète. L'anomalie excentrique de Huygens s'exprime alors en fonction du temps par illustratie ou, en unités modernes, par illustratie.

 

Il en résulte que la vitesse variable v de la planète dans son orbite circulaire s'exprime suivant Huygens par la formule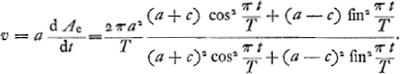



illustratie

Pour le rapport des vitesses aux apsides (aphélie et périhélie) on a toujours, comme chez Kepler et Ward illustratie.

Ce n'est donc pas dans le but de corriger tant soit peu l'équation v1 : v2 = 1/r1 : 1/r2 dans le sens de l'équation v1 : v2 = 1/√r1 : 1/√r2 que Huygens a conçu son hypothèse.

Nous remarquons en passant que les vitesses aux apsides elles-mêmes sont différentes suivant les trois hypothèses. On a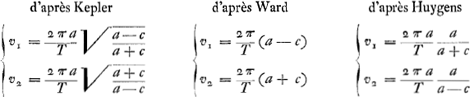



illustratie

C'est dans les §§ 13 et 14 qui suivent que Huygens explique l'agencement fort ingénieux des roues à dents égales servant à ‘invenire’ - ‘proxime’ du moins - ‘ex anomalia media coequatam’ (mais il est évident qu'on peut aussi, § 17, obtenir un mouvement de vitesse variable en se servant de dents inégales). On trouve aussi un passage sur ce sujet dans la ‘Descriptio’ du planétaire publiée en 1703, mais ce passage ne contient pas toutes les considérations mathématiques du présent texte. La construction a-t-elle suffisamment attiré l'attention des astronomes? Nous en doutons. Tout mathématicien ou astronome qui a jeté les yeux sur la ‘Descriptio’ a dit son mot sur les fractions continues (qui se trouvent au § 16 qui suit et dont pour le moment nous ne traiterons pas). Mais il vaut aussi la peine de constater, comme nous le ferons ici, qu'il est vrai, ainsi que le dit Huygens, que la machine tire de l'‘anomalia media’ l'‘anomalia coequata’ à fort peu près suivant les équations de Kepler.

Dans les §§ considérés Huygens donne le nom d'‘anomalia coequata’ à la grandeur Ac de Kepler, non pas à la sienne. C'est pourquoi nous désignerons ici celle de Kepler simplement par Ac. De même pour Ae.

Nous ne copions pas ici l'explication de Huygens mais nous la suivons de près, la mettant en équations à la façon moderne. Dans sa figure, où le soleil se trouve en E et où les droites EH et DK sont parallèles, il démontre que suivant la loi des aires de Kepler - il est vrai que dans le planétaire la planète se trouve en K, point de la circonférence de cercle AKC, et non pas en N, point de l'ellipse; mais il faut avoir égard au fait que le secteur EKC lorsque K se trouve sur la même verticale que N (AC étant horizontale), est toujours à l'aire correspondante ENC dans le même



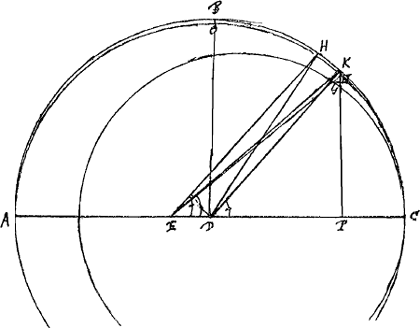illustratie

rapport grand axe/petit axe, de sorte que la loi des aires est valable aussi pour ces secteurs de cercle - lorsque l'arc HC est l'‘anomalia media’ donnée, l'arc KC sera à fort peu près l'‘anomalia excentri’ de Kepler, non pas exactement puisque dans la démonstration le triangle rectiligne EHK a été posé égal au triangle curviligne EHK. Le reste du raisonnement est exact.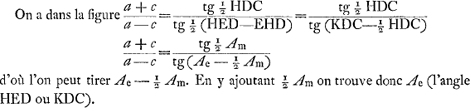

illustratie

On a de plus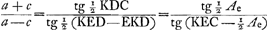

illustratie

On en tire KEC - ½ Ae, et en y ajoutant ½ Ae on trouve l'angle KEC. Or, l'‘anomalia coequata’ Ac est telle que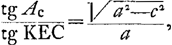

illustratie

de sorte qu'on peut maintenant calculer ou construire Ac.

D'après ces équations on a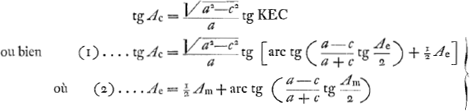



illustratie

La formule (1) ne peut être qu'une autre forme de celle de Kepler exprimant Ac en fonction de Ae savoir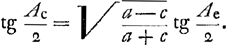

illustratie

En développant, on verra que les deux formules sont en effet parsaitement identiques.

 

Quant à la formule (2), nous avons vu plus haut que d'après sa théorie à lui Huygens obtient - ou aurait pu obtenir - l'équation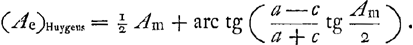

illustratie

Les deux équations sont absolument identiques. Il paraît donc qu'on a - abstraction faite de la petite inexactitude qui consiste à prendre le triangle rectiligne EHK égal au triangle curviligne EHK -

 

(Ae)Huygens = (Ae)Kepler,

ce qui veut dire que dans la figure, ou dans l'automate, la planète de Huygens coïncide toujours à fort peu près avec la planète de Kepler, bien entendu avec la planète de Kepler transportée du point N de l'ellipse au point K de la circonférence de cercle suivant une petite droite NK parallèle au petit axe de l'ellipse. Il semble bien qu'en 1680-1681 Huygens était en droit de penser que sa première équation à lui, ou plutôt l'ensemble de ses deux équations, se montrerait ‘fortasse propior veritati’ que celles de Kepler.

 

Nous croyons encore devoir remarquer que Huygens a fait une faute de calcul à la p. 4 du Manuscrit F (comparez la note 38 de la p. 121) en écrivant que pour Am = 45o l'anomalie excentrique aurait pour Kepler la valeur 37o46′, car pour c/a = 21/100 - il s'agit, comme nous avons dit, de la planète Mercure - c'est la valeur 37o38′

qui satisfait à l'équation de Kepler 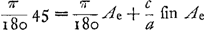illustratie. Il n'y a donc pas ici, comme il le dit, une différence de 8′ entre l'anomalie excentrique de Kepler et la sienne, au contraire les deux valeurs s'accordent exactement39).

 

Une note ajoutée par Huygens en 1688 aux pages considérées (§ 12 qui suit) fait voir, ce que nous avons déjà dit au début du présent Avertissement, qu'après l'apparition des ‘Principia’ de Newton il accepta la théorie de ce dernier et abandonnna par conséquent toute autre hypothèse que celle de Kepler sur la variation de la vitesse des planètes. Comparez sa note de 1689 (§ 7 à la p. 310 du T. XIX) s'appliquant aux comètes où il dit accepter désormais, également avec Newton, l'idée que celles-ci se meuvent, non pas en lignes droites, mais en ellipses (bien entendu, en ellipses possédant, elles, de grandes excentricités) comme les planètes.

 

Au § 11 Huygens avait exprimé une autre idée, celle que l'orbite d'une planète, de la terre p.e., pourrait ne pas être précisément ni une ellipse ni une circonférence

de cercle (de l'avis de Boulliau aussi40) la forme elliptique de toutes les orbites n'avait pas encore été démontrée); ceci dans le but - ou plutôt dans le vague espoir - d'obtenir pour les vitesses aux apsides l'équation désirée v1 : v2 = 1/√r1 : 1/√r2. Il semble du moins qu'il n'avait pas développé cette hypothèse plus longuement.

 

Nous ne disons rien ici des §§ 17-22 où Huygens traite de détails techniques pratiquement importants sans doute, mais qui ne peuvent, pensons-nous, intéresser la majeure partie de ceux qui s'occupent de l'histoire des sciences autant que ses vues théoriques.

 

Nous ne croyons devoir ajouter quelques mots encore que sur la question de savoir pourquoi Huygens différa durant de longues années la rédaction de la ‘Descriptio’ du planétaire achevé en 1682; et aussi sur l'histoire des orbites circulaires excentriques.

Il nous semble, en considérant des Pièces telles que les ‘Pensees meslees’ - de 1686? - qu'on trouve plus loin dans le présent Tome, que Huygens avait vaguement l'intention - de même qu'il en a été longtemps pour la théorie du mouvement, ainsi que pour la dioptrique et la théorie générale de la lumière qu'il voulait réunir en un tout avec le traité sur les couronnes et les parhélies - de joindre la description de l'automate à un ouvrage astronomique plus grand, et que ce ne fut que plus tard que - désespérant de mener à bonne fin la composition d'oeuvres si vastes - il se résolut à écrire séparément l'Addition au discours de la cause de la pesanteur, le Cosmothéoros, et la Description du planétaire.

Quant aux orbites circulaires excentriques, Huygens avait dans sa jeunesse étudié le système de Copernic - ou plutôt un système se rattachant à celui de Copernic - dans les oeuvres de Philippus van Lansbergen ou Lansbergius41). Dans les ‘Theoricae motuum coelestium novae, & genuinae’ de ce dernier42) l'auteur explique qu'à son avis les trois planètes supérieures, Saturne, Jupiter et Mars décrivent avec une vitesse uniforme autour du soleil des excentriques dont les centres se déplacent uniformément sur certains ‘circelli’. Pour Vénus et Mercure la théorie ‘nonnihil differt à Theoria motus trium superiorum Planetarum’. Vénus se meut toujours sur un cercle excentrique, Mercure sur un épicycle dont le centre décrit un excentrique.

En 165343) Huygens fit connaissance avec la ‘Nederduytsche Astronomia’ de cette année de D. Rembrantsz. van Nierop, copernicain et partisan des tourbillons de Descartes44), qui cite aussi e.a. van Lansbergen, ainsi que l'‘Astronomia Danica’ de Chr. Longomontanus, élève de Tycho Brahé45) et maintenant comme lui la terre au centre du monde, tout en lui donnant le mouvement diurne de rotation que Brahé lui refusait. Pour Longomontanus, comme pour Brahé, les planètes tournent autour du soleil. Dans le ‘Lib. Sec. Theoricorum, de motibus reliquorum [c.à.d. autres que le soleil et la lune] quinque planetarum restitutis’ il n'admet pas les ellipses de Kepler, voulant maintenir, comme Ptolémée et Copernic, ‘quod motus corporum coelestium sit aequalis et circularis perpetuus vel è circularibus compositus’, ce qui donne lieu, de même que dans l'Almageste, à des constructions compliquées.

Quant à van Nierop, nous46) avons dit à la p. 517 du T. XV que celui-ci fait tourner les planètes dans des excentriques autour du soleil, tout en reconnaissant que la théorie du mouvement elliptique, telle que l'admet Kepler, est, par opposition à sa propre théorie, ‘correcte [nous soulignons], mais compliquée et laborieuse’.

L'auteur du présent Avertissement n'est pas de cet avis. C'est bien dans des excentriques que, d'un mouvement non-uniforme, van Nierop fait tourner les planètes, et il reconnaît (p. 170-171) que ceci n'est à peu près exact que durant 2000 ou 3000 ans (‘na genoegh in dese twee of drie 1000 jaer’); c'est pour cela, dit-il, que Kepler fait son culcul etc. (‘Hierom ist dat I. Keplerus sijn rekeninghe maeckt, etc.’). Mais ‘dit was wel prijselijck / bij soo veer de bewegingh in selfs volkomenheydt hadde / ende dan wel juyst bekendt was / 't welck doch geen van beyden is / daerom met recht onnodigh geacht’, ce qu'on peut traduire comme suit: ‘Ceci était certainement louable, pour autant que le mouvement eût possédé en lui-même de la perfection, et qu'il fût parfaitement connu, ce qui pourtant n'est pas, ni l'un ni l'autre, par conséquent à bon droit jugé inutile.’ A la p. 39 de l'Appendice (‘Aenhangh’) van Nierop dit, après avoir parlé de la théorie de Copernic: ‘Hier nae I. Keplerus de Planeten in een Ellips of lank-ront gestelt te lopen / waer me dat men oock na genoegh tot het begeerde kan geraken’ (Après lui Kepler a posé que les planètes parcourent une ellipse, moyennant quoi on peut aussi parvenir à peu près au but désiré).

Ce n'est donc apparemment pas dans van Nierop que Huygens eût pu puiser la conviction que la théorie de Kepler est de toutes la plus exacte.

Bientôt après 1653 Huygens construisit sa ‘tabula lignea’ ou plutôt ses deux ‘tabulae ligneae’ aujourd'hui perdues qui représentaient les orbites planétaires47). On peut, nous semble-t-il, les considérer comme dérivés directement du ‘Planeetwyser om de plaetsen der planeeten in lengte en brete te vinden’, grande figure qui se trouve dans la ‘Nederduytsche Astronomia’, où les planètes, comme nous l'avons dit, parcourent des excentriques autour du soleil48). Mais il ne s'agissait pas d'une simple copie puisqu'il fut question en avril 1673 d'une publication de ces tables de Huygens: voyez, aux p. 270-276 de notre T. VII, sa lettre à un certain Royer, où l'on voit aussi que Huygens avait introduit dans ses ‘tabulae ligneae’ des données des Tables Rudolphines de Kepler. Or, comme Huygens ne dit point dans cette lettre que les planètes, ou certaines planètes, décrivent des ellipses, ce qu'il n'aurait

guère pu taire s'il en avait été ainsi, il appert que les ‘orbites’ dont il parle étaient des cercles excentriques, parcourus d'un mouvement non-uniforme. Voyez aussi dans la l. 6 de la 271 du dit T. VII l'expression ‘chemin orbite ou Eccentrique’ et dans la deuxième ligne d'en bas de la p. 273 l'expression ‘cercles ou orbites’.

C'est ce mouvement non-uniforme, croyons-nous pouvoir ajouter, que Huygens a précisé et mis pour ainsi dire en équation dans son planétaire. On peut remarquer que la construction de la longitude d'une planète des ‘tabulae ligneae’, telle que la décrit le troisième alinéa de la p. 271 du T. VII, est identique avec celle de la figure de la p. 126 qui précède. Cette construction se rattache, comme on peut le voir à la p. 143 qui suit, à une construction de Cavalieri dans son ‘Directorium generale uranometricum’ de 163249) que Huygens connaissait déjà avant 165750) et qui a donc peut-être eu une certaine influence sur lui.


Vorige Volgende