Oeuvres complètes. Tome XXI. Cosmologie

[p. 53]

Appendice IV
À Huygens à l'Académie Royale des Sciences.
Astronomie.
[1674]

La présente page du Manuscrit E¹⁾ fait bien voir, comme nous l'avons dit à la p. 14 qui précède, que lors de leur commun séjour à Paris, Huygens et Roemer conversaient sur des sujets d'astronomie. Comme nos notes le font voir, Huygens n'a pas pris la peine de bien rédiger cette Pièce.

P. 7. Römer. Supposito [Fig. 9] angulo in sole ACB (à circulis per verticem et per polum) altitudinis variatio est ad tempus (tempus scilicet quo arcus variationis

[Fig. 9].

altitudinis mergitur infra parallelum horizontis per solem transeuntem) ut AB ad

1) Manuscrit E, p. 7. La p. 26 porte la date du 19 décembre 1674.

[p. 54]

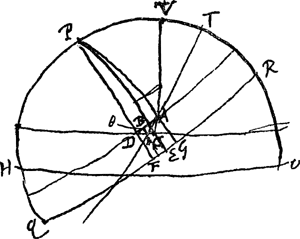
AC. Declinationis variatio est ad tempus (tempus quo arcus variationis declinationis mergitur infra eundem horizontis parallelum per solem transeuntem) ut BA ad BC²⁾.

HPVO meridianus. V vertex, P polus. PCV angulus in sole [c'est l'angle qui plus haut s'appelait ACB]. QR aequator. DA parall. aequ. HO horizon. DC parall. horiz.

AC variatio altitudinis³⁾.

GF arcus aequatoris seu tempus quo punctum A serius attinget parallelum horiz. CD quam punctum C.

BC variatio declinationis⁴⁾.

EF tempus quo punctum B serius attinget parall. horiz. DC quam punctum C⁵⁾.

Ergo variatio altitudinis AC ad tempus GF non est ut AC ad AD hoc est ut BA ad AC, nisi cum arcus AD non differt à GF, hoc est, cum sol est in aequatore.

Itemque variatio declinationis BC⁴⁾ ad tempus FE non est ut BC ad BD, h.e. ut BA ad BC nisi cum arcus BD non differt ab EF, hoc est cum sol est in aequatore.

Sole autem non in aequatore posito, erit ratio AC ad GF composita ex AC ad AD, seu BA ad AC, et ex DA ad FG, hoc est et ex ea quam habet sinus arcus PA ad sinum totum⁶⁾.

2) Ici le soleil est donc supposé se trouver au point C. Quant à la ‘variatio’ de sa hauteur, elle résulte apparemment d'un déplacement fictif du soleil, indépendant du mouvement diurne, avec une vitesse constante v de C en A, en un temps CA. Si AD désigne le temps dans lequel le point A est transféré en D par suite du mouvement diurne, la vitesse nommée v étant supposée égale à la vitesse linéaire de ce dernier mouvement du point A, on a:
altitudinis variatio CA (temps): temps AD (ou plus brièvement CA : AD) = AB : AC, puisque dans le petit triangle rectangle DCA CB est la perpendiculaire sur l'hypoténuse. On aura de même, en supposant cette fois que la vitesse du mouvement CA soît telle que la composante CB de ce mouvement ait la vitesse v susdite (ou bien que le soleil se déplace de C en B avec cette vitesse v):
declinationis variatio CB (temps): temps BD (ou plus brièvement CB : BD) = AB:CB (même triangle).
C'est dire qu'il est bien plus simple de ne considérer que les relations géométriques CA : AD = AB : AC et CB : BD = AB : CB sans parler de temps ni de vitesses.

3) TAI (voyez la suite du texte) représente l'écliptique dont un point déterminé vient en I (point de la circonférence de cercle CD parallèle à l'horizon) après un certain temps. Le soleil qui au commencement de ce temps, p.e. à midi, se trouvait par hypothèse au point considéré de l'écliptique ne vient cependant pas en I en ce temps, mais seulement en A par suite de son mouvement propre dans l'écliptique. L'arc IA est considéré comme une ‘variatio’ dans la position du soleil à laquelle correspondent la ‘variatio altitudinis’ CA (ou AC) et la ‘variatio declinationis’ I θ (ou θ I), θ étant le pied de la normale abaissée de I sur AD.
Il est évident qu'il n'est plus question désormais d'un ‘angulus in sole ACB’, c.a.d. d'un soleil se trouvant au point C.

4) Comme la suite du texte le fait voir la véritable ‘variatio declinationis’ n'est cependant pas CB ou BC (note 2) mais I θ ou θ I (comparez la note 3).

5) Nous avons corrigé ‘punctum B’ en ‘punctum C’.

4) Comme la suite du texte le fait voir la véritable ‘variatio declinationis’ n'est cependant pas CB ou BC (note 2) mais I θ ou θ I (comparez la note 3).

6) Rapport que nous désignons aujourd'hui simplement par sin PA.

[p. 55]

Et ratio BC ad FE, componetur ex ratione BC ad BD seu AB ad BC et ex BD ad FE, quae est ea rursus quae semis arcus PA ad sinum totum.

Dum punctum eclipticae T à meridiano venit in I, sol fecisse putetur arcum IA. tunc enim variatio altitudinis erit CA. variatio declinationis erit ϑI³⁾⁴⁾.

Habentur duae solis altitudines aequales ante et post meridiem, et tempora utriusque observationis notata horologio quod ad mediam dierum mensuram temperatum est. Quaeritur quam horam indicante horologio sol fuerit in meridiano. Datur declinatio solis et poli altitudo praeter altitudines solis observatas: Item variatio altitudinis solis in dato exiguo tempore, puta 1′. Hinc angulus in sole, et reliqua absque calculo triangulorum secundum methodum Romeri.

Les considérations qui précèdent n'étant pas sussisamment explicites, il ne nous est pas possible d'indiquer quelle était précisément la ‘methodus Roemeri’ servant à résoudre le problème proposé.

En 1668 Huygens avait déjà résolu le même problème en se servant du ‘calculus triangulorum’: voyez, à la p. 369 du T. XVIII, la Pièce intitulée: ‘Ad inveniendas longitudines in mari, ex duabus aequalibus solis altitudinibus et hora pendulorum’ qui constitue notre Appendice I à la Pars Prima de l'‘Horologium oscillatorium.’ Cette Pièce est parfaitement claire. La note 2 que nous y avons ajoutée fait voir que là aussi Huygens parle d'un soleil se trouvant en un certain point 1 de la Fig. 119 où le soleil ne se trouve pas en réalité: ce point 1 nous semble analogue au point C de la présente Fig. 9 où le soleil est dit se trouver (voyez la note 3 de la p. 54) sans qu'il en soit ainsi.

3) TAI (voyez la suite du texte) représente l'écliptique dont un point déterminé vient en I (point de la circonférence de cercle CD parallèle à l'horizon) après un certain temps. Le soleil qui au commencement de ce temps, p.e. à midi, se trouvait par hypothèse au point considéré de l'écliptique ne vient cependant pas en I en ce temps, mais seulement en A par suite de son mouvement propre dans l'écliptique. L'arc IA est considéré comme une ‘variatio’ dans la position du soleil à laquelle correspondent la ‘variatio altitudinis’ CA (ou AC) et la ‘variatio declinationis’ I θ (ou θ I), θ étant le pied de la normale abaissée de I sur AD.
Il est évident qu'il n'est plus question désormais d'un ‘angulus in sole ACB’, c.a.d. d'un soleil se trouvant au point C.

4) Comme la suite du texte le fait voir la véritable ‘variatio declinationis’ n'est cependant pas CB ou BC (note 2) mais I θ ou θ I (comparez la note 3).