Oeuvres complètes. Tome XXI. Cosmologie

[p. 48]

Appendice III
À Huygens à l'Académie Royale des Sciences.
Astronomie.
[1666]¹⁾

A. Trouver la distance de la terre a la lune, par le diametre apparent de la lune observè a deux differentes heures en un mesme jour ou nuict et sa hauteur prise en mesme temps.

L'on suppose que l'observation du diametre apparent se fasse avec une tres grande exactitude par le moyen des filets tendus dans une lunette d'approche, au foier du verre oculaire; et d'autant qu'il y aura plus de difference de hauteur de la lune aux 2 ob-

[Fig. 8]

1) Manuscrit C, p. 124-126. Les p. 110 et 128 du Manuscrit C portent respectivement les dates du 2 nov. et du 31 déc. 1666.

[p. 49]

servations d'autant plus precis sera le calcul. Et le mieux est de les faire alors que la lune est pres de son apogee ou perigee a cause que sa distance ne varie pas sensiblement alors entre la premiere et derniere observation.

Soit D [Fig. 8] le centre de la lune, A le centre de la terre, joints par la droite AD, et qu'un plan menè par ces 2 centres couppe la terre et fasse le cercle EFG.

Or il faut scavoir, que puis qu'on suppose qu'aux deux observations la distance de la lune au centre de la terre est la mesme, que la grandeur du diametre apparent de la lune depend uniquement de l'angle de sa hauteur sur l'horizon, en sorte que cet angle estant plus petit, le diametre apparent sera plus petit aussi, a cause que la distance sera plus grande entre la lune et l'observateur.

Soit maintenant le premier lieu de l'observateur en E d'ou la lune D aie paru elevee sur l'horizon de l'angle DES de 12 degr. et son diametre apparent de 30′.27″. Et que quelques heures apres, le mesme observateur, mais transportè par le mouvement journalier de la terre en V, aie observè la hauteur de la lune de 56 degr. et son diametre apparent de 30′.44″. Il est certain que si au temps de la premiere observation en E un autre observateur se fut trouvè a un point du cercle EFG, prenons que ce soit en F, ou la lune D luy eust paru elevee sur l'horizon de 56 degr. il est certain, dis je, qu'il y auroit veu son diametre apparent de 30′.44″. parce que comme j'ay dit, ce diametre depend uniquement de la hauteur plus ou moins grande de la lune sur l'horizon, en sorte que de quelque lieu qu'on l'observe haute de 56 degr. son diametre y paroistra de 30′.44″. Pour trouver donc la distance DA, nous supposons que au mesme temps qu'on a observè la lune du point E ou elle estoit haute de 12 degr. et son diametre apparent de 30′.27″, un autre observateur l'a observée du point F, ou elle avoit la hauteur de 56 degr. et d'ou nous scavons certainement que son diametre devoit paroistre de 30′44″, et ces suppositions faites, je trouve la regle suivante pour calculer la distance AD.

Regula.

Sit data, ex diametrorum ratione, major distantia lunae ED ad minorem FD quae 100000 ad 99078. Fiat ut DE ad DF ita sinus altitudinis majoris DFT ad aliam, à qua auferatur sinus altitudinis minoris DES. Et ut residuum ad differentiam distantiarum ED, FD, ita erit earum summa dimidia ad semidiametrum Terrae, in partibus qualium distantia major posita fuit 100000. Hinc vero et distantia DA data erit, quippe quae sit hypotenusa trianguli rectanguli AOD, cujus latus unum DO est sinus compl. minoris altitudinis observatae, alterum vero OA sinus ipse ejus altitudinis junctus terrae semidiametro EA.

[p. 50]

Demonstratio Regulae praecedentis.

Producantur AF, AE, sint ijs perpendiculares DN, DO. Et in recta FN sumatur FR aequalis EO [Fig. 8].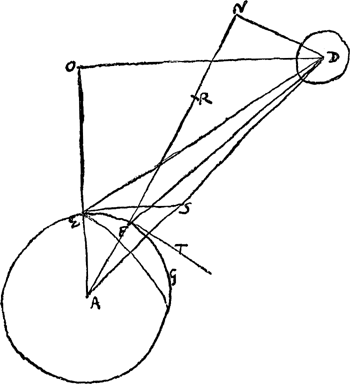

[Fig 8]

Quadr. AD aequatur quadratis AF, FD et duplo ▭^o AFN. At idem qu.AD aequatur qu.^is AE, ED, et duplo ▭^o AEO. Ergo qu.^a AF, FD, cum duplo ▭ AFN, aequalia qu.^is AE, ED cum duplo ▭^o AEO. Et ablatis utrinque qu.^is aequalibus AF, AE, erit qu. FD cum duplo rectang. AFN aequale qu^o ED cum duplo ▭ AEO. Unde si rursus aequalia conferantur, hinc nimirum dupl. ▭ AEO, inde dupl. ▭ AFR; Relinquetur qu. ED aequale qu. FD cum duplo ▭ AF, RN. Itaque qu. ED superat qu. FD hoc duplo ▭ AF, RN. Est autem idem excessus qu.ⁱ ED supra qu. FD aequalis rectangulo ex summa et differentia duarum ED, FD. Ergo et ▭ ex AF, RN aequabitur ▭^o ex differentia duarum ED, FD. Ideoque erit ut RN ad differentiam duarum ED, FD, ita earum summa ad duplam AF. Quia vero datur, ex diametrorum observatione, ratio ED ad FD; Sequitur, si ponatur ED partium 100000, etiam FD in talibus partibus datam esse, adeoque et summam utriusque et differentiam. Sed et rectam NR quae est differentia duarum NF, OE datam esse in similibus partibus sic ostendetur. Etenim quia anguli altitudinis lunae supra horizontem in utraque observatione dati sunt DES, DFT, et angulo quidem DES aequalis est

[p. 51]

angulus EDO in triangulo rectangulo EOD. patet posita ED partium 100000 fieri EO sinum anguli EDO seu DES, ideoque datam esse. Caeterum et FD cum data sit, et data item ratio ejus ad FN, nempe ea quae est radij ad sinum anguli dati FDN ipsi DFT aequalis; patet et FN datam fore, invenirique ipsam faciendo ut sicut radius ad sinum FDN ita FD ad aliam. Itaque auferendo datam EO sive ipsi aequalem FR ab FN data, etiam reliqua RN dabitur. Et faciendo itaque ut RN ad differentiam duarum ED, FD ita earum summa ad aliam, ea erit dupla AF; quae itaque dabitur in partibus qualium ED erat 100000.

B²⁾. Trouver la distance de la Lune au Centre de la Terre par deux Observations de son diametre apparent, et ses hauteurs sur l'horizon, prises en mesmes temps. Supposè que la distance entre la Lune et le centre de la terre soit la mesme aux deux Observations.

Regle.

Les distances de la Lune à l'observateur estant en raison contraire des diametres observez, L'on fera comme la plus grande distance (que l'on supposera egale au Rayon, par exemple de 100000 parties) est à la moindre distance, ainsi le sinus de la plus grande hauteur de la Lune à une quatrieme; de la quelle on ostera le sinus de la moindre hauteur de la Lune; et comme le reste est a la difference des deux distances, ainsi sera leur somme au diametre de la Terre. En suite de quoy l'on connoistra aussi la distance requise de la Lune au centre de la Terre; car ce sera l'hypotenuse d'un triangle rectangle, dont l'un costè est le sinus du complement de la moindre hauteur observee, et l'autre composè du sinus mesme de cette hauteur, et du demidiametre de la Terre.

Si la hauteur estant de 12 degr. le diametre de la Lune est de 30′.27″.

Et la hauteur estant de 56 degr. le diametre est de ..... 30′.44″.

L'on trouvera par cette methode que la distance de la Lune au centre de la Terre est environ de 33 diametres de la Terre.

2) La partie B de cet Appendice est empruntée à la p. 253 du Manuscrit E. La p. 254 porte la date du 24 novembre 1680, mais comme il s'agit dans le cas de la p. 253 d'une feuille collée dans le Manuscrit, sa date est incertaine. Elle nous semble être de 1666 bien plutôt que de 1680 puisque la règle, ainsi que les données numériques, sont absolument les mêmes que celles de la partie A qui précède.

[?]

C³⁾. De 60 pieds ouverture de 6 p. 8 l. 240 fois.

qui fait 60 .. ouverture de 4. .... 200 fois, avec un oculaire de 3⅗ pouce

3) La partie C est empruntée à la p. 257 du Manuscrit E. Il s'agit ici aussi (comparez la note 2) d'une feuille collée dans le Manuscrit. La date étant donc incertaine, nous avons cru pouvoir la reproduire ici.

[p. 52]

fait voir le diametre de la lune de 100 degr. puisqu'elle est d'un ½ degr. C'est a dire 500 lieues d'Allemagne sous l'angle de 100 degr. ou 5 lieues sous 1 degr. ou 1 lieue sous 12 min.

1 degrè est la 1/57 partie de sa distance de l'oeil, donc a la distance de 57 pouces c'est pres de 5 pieds l'on verra un rond d'un pouce de diametre de mesme qu'une tache de la lune qui a 5 lieues de diametre.

Et 2⅖ lignes, a cette mesme distance de 5 pieds, comme une chose dans la lune de l'estendue de 1 lieue. Et une chose de ½ lieue, comme seroit la ville de Paris, comme 1⅕ lignes à la distance de 5 pieds.

Comparez avec la présente Pièce C la p. 351 du T. VII (lettre de Huygens à Colbert du 9 août 1673).