Oeuvres complètes. Tome XXI. Cosmologie

[p. 43]

Appendice II
À Huygens à l'Académie Royale des Sciences.
Astronomie.
[1666]¹⁾

Nous avons fait mention de cet Appendice aux p. 27 (fin du § 2) et 28 (§ 4) qui précèdent.

Immédiatement après avoir dressé pour l'Académie le programme qu'on trouve aux p. 255-257 du T. XIX²⁾, Huygens remplissait quelques pages du même Manuscrit³⁾ de remarques sur les observations astronomiques. Ce sont les Pièces A - G qui suivent. On y trouve e.a. les brouillons des Pièces destinées à l'Académie qui constituent les §§ 2-5 et 8 de la Pièce I qui précède.

1) La p. 102 du Manuscrit C porte la date 1666 Sept. et la p. 107 est datée 2 Nov. 1666.

2) Manuscrit C, p. 92-93.

3) P. 94-95, 98-101 et 107-109.

A.

P. 94. Si on mene un plan par le soleil la lune et l'oeil, les cornes visibles de la lune sont dans la ligne perpendiculaire au dit plan.

Suit un passage biffé qui fait voir que Huygens venait d'avoir une conversation, sans doute avec un de ses collègues (Auzout?), sur des sujets astronomiques: Il me semble qu'il a dit que lors que le plan menè par l'estoile et les cornes de la lune, vues de l'estoile, passe par Paris, que c'est au même instant que l'observateur de Paris voit les cornes de la lune avec l'estoile en ligne droite. Ce qui n'est pas vray.

Voyez encore quelques remarques sur la lune dans l'Appendice IV qui suit.

B.

P. 95. Radij per lineas rectas. In diversorum diaphanorum communi superficie frangitur radius (aliqui reflectuntur) solidi et liquidi. liquidum aer et aqua. magis et minus, non a densitate seu pondere pendet, cum oleum majorem faciat refractionem quam aqua, etsi sit levius. Primi per angulos, deinde per sinus. Snellij figura consentit cum

[p. 44]

lege sinuum. refractiones in perpendiculari etiam statuit. male. quid eum fefellerit. Modus explorandi refractiones in solidis diaphanis. Alij modi ex supposito principio.

Voyez sur les rayons droits et la réfraction atmosphérique la Pièce V qui précède (p. 37). On peut consulter aussi les p. 2-9 et 155-156 du T. XIII et 457 du T. XVII.

C.

P. 95. Non mirum est inventum telescopij tot seculis latuisse, et casu demum ac non ratione repertum fuisse, cum quod principia refractionum vera eruere non parvam difficultatem haberet, tum quod jam datis difficillimum esset inde deducere quinam vitreorum sphaericas superficies habentium ac diverfimodo compositorum futuri essent effectus. Si enim cognita jam telescopij constructione nihilominus obscura adeo fuit ejus demonstratio, ut a plurimis tentata necdum perfecta fuerit, hoc enim vere dicere possumus, combien doit on penser qu'il aie estè au dessus de l'intelligence des hommes de concevoir et la forme et l'assemblage requis de verres qui devoient augmenter et comme approcher les objects eloignez, ou faire discerner d'autres invisibles a raison de leur petitesse, comme nous voions que font les telescopes et microscopes.

Sur l'invention des télescopes etc. on peut consulter le T. XIII. Voyez aussi la l. 6 de la p. 664 du T. XVIII.

D.
P. 98. Pour prendre la hauteur du pole.

Observer la plus grande hauteur du soleil ou de quelque estoile dont la declinaison est cognue. Si elle est boreale, ostez la declinaison de la plus grande hauteur observee. le complement du reste a 90 degr. sera la hauteur du pole.

Si la declinaison est australe adjoutez la a la hauteur plus grande, et le complement de la somme a 90 degr. sera la hauteur du pole.

E.
P. 98. Trouver la ligne meridiene independemment.

Ayez un fil perpendiculaire sur un plan nivellè, et du mesme point ou il est attachè ayez un autre fil mobile que vous tendrez a quelque angle que ce soit jusques au plan nivellè et observez par ces deux fils l'azimuth le plus oriental et apres aussi le plus occidental de quelque estoile qui passe du costè boreal du zenith comme il y a pour icy la pluspart de celles de la grande ourse, de Cassiopée, Cepheus, la petite ourse; et ces deux observations se peuvent faire en une mesme nuit en 6 ou 7 heures d'intervalle. Apres il n'y a qu'a diviser par le milieu l'angle que font ces deux azimuts au point de la perpendiculaire, et l'on aura la ligne meridiene.

[p. 45]

D bis.
P. 98. Ayant la meridiene trouver la hauteur du pole.
Observer la hauteur du pole.

Observez la plus grande et la plus petite hauteur d'une estoile fixe de celles qui sont vers le pole comme il y en a en l'ourse et en Cassiopée qui ne descendent pas plus bas que 30 degr. et partant sont libres de refraction sensible. La moitiè de la difference de ces hauteurs jointe a la moindre donnera la hauteur du pole. Ces 2 observations se peuvent souvent faire en 6 semaines d'intervalle.

Consultez la note 29 de la p. 15 de l'Avertissement qui précède sur la thèse - provisoirement admise par Huygens - qu'on peut négliger l'erreur due à la réfraction atmosphérique pour les astres dont la hauteur est supérieure à 30^o.

E bis.
P. 99. Maniere independante pour trouver la ligne meridiene.

Par le moyen d'un fil perpendiculaire sur un plan horizontal l'on observera et tracera l'azimut le plus oriental ..... etc.

C'est le brouillon du § 2 de la Pièce I qui précède (p. 26). Nous ne reproduisons pas le brouillon en entier puisque le dit § 2 s'accorde presque mot à mot avec lui.

Il nous semble que la partie E bis est antérieure à la partie E puisque E bis est pleine de ratures ce qui n'est pas le cas pour E.

F⁴⁾.
P. 100. Trouver la refraction du soleil.

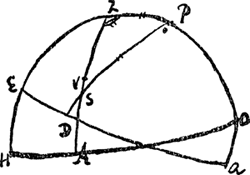
[Fig. 4]

Nous répétons ici la Fig. 4 du § 8 de la Pièce I, avec laquelle celle du présent brouillon s'accorde.

Soit HZ le meridien, Z le zenit. P le Pole. S le soleil sans refraction, V avec refraction. On prendra l'azimut du soleil AH (car avec ou sans refraction ce sera toujours le mesme) et sa hauteur AV en mesme temps. Et premierement scachant l'heure qu'il est par le moyen d'une pendule, l'on connoistra par là la declinaison du soleil, et son complement qui est l'arc PS.

4) Huygens biffa cette partie.

[p. 46]

outre lequel on connoit aussi dans le triangle SZP le costè PZ qui est le complement de la hauteur du pole, et l'angle Z par l'observation de l'azimut, donc on calculera par la le costè PZ, dont le complement est SA, et ayant soustrait SA de VA, la difference SV sera pour la refraction du soleil a cette hauteur-la.

G.
P. 100. Distantiam lunae a terra invenire, unde et parallaxis quantitas cognoscitur.

À l'Académie, en 1666 ou 1667, on traita de la parallaxe de la lune: voyez le § 7 à la p. 30 qui précède. Les Registres ne disent pas que Huygens ait pris part à la discussion, ce qui toutefois peut fort bien avoir été le cas. Voyez aussi à la p. 566 du T. XV son calcul de 1665 sur le même sujet.

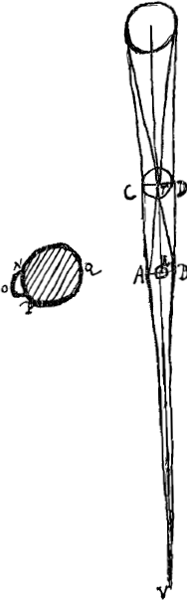
[Fig. 7]

In eclipsi lunae observetur cujus circuli portio sit umbra terrae NP [Fig. 7] cum circiter dimidiam lunam obtegit. hoc autem vel per maculas lunae dignoscetur, vel variae magnitudinis circulos intra telescopium in foco lentis ocularis visui obtendendo atque ad visam speciem umbrae NP applicando [comparez les premières lignes de la p. 19 qui précède]. Poterit autem et exactius forsan ex cognita positione eclipticae viaeque lunaris et ex mora eclipsis circulus umbrae cognosci cum motus lunae a sole satis prope cognitus sit, vel etiam absque illo si distantia solis a nodo satis exacte cognita ponatur. Capta deinde post vel ante eclipsin, lunae diameter, facile magnitudo diametri umbrae cum illa conferetur, adeoque scietur quo angulo ex terra nobis spectetur, quo dato dico et distantiam lunae a terra dari. Sit enim T terra, L luna, conus umbrae CVD, diameter umbrae in lunae transitu AB. Est ergo angulus V ad verticem coni aequalis ei sub quo sol nobis spectatur quia immensa est solis distantia ad distantiam lunae comparata vel etiam ad totius coni CVD longitudinem (vel si parallaxis solis aliqua detur⁵⁾ ejus duplum, hoc est dupla parallaxis hori-

5) En 1688 Huygens évalua avec Cassini, d'après les observation de celui-ci, la parallaxe du soleil (‘la parallaxe’ est dit couramment, comme on sait, pour désigner ‘la parallaxe horizontale’) à 10″18‴ (voyez la p. 410 qui suit); plus tôt, en 1659, sans observation directe à environ 8″ ce qui est fort proche de la vraie valeur; voyez les p. 192, 347 (note 7) et 378 du T. XV. ou bien la p. 308 qui suit Consultez aussi sur la vraie valeur la note 7 de la p. 397 du T. XIX.

[p. 47]

zontalis⁵⁾ ablata ab angulo sub quo sol nobis spectatur dabit angulum coni V). Itaque datus est angulus V, 31′ ex. gr. Sed et angulus ATB sub quo diameter umbrae specctatur datus est. puta 1.25′. Ergo et ratio VL ad LT data erit, eadem proxime ob exilitatem angulorum quae anguli ATB ad AVB, hoc est quae 85 ad 31. Sed tota TV data est in diametris terrae ob angulum V datum 31′ estque circiter VT ∞ 114 CD. Ergo si siat ut 85 + 31 ad 31, hoc est ut 116 ad 31, ita 114 ad aliud nempe 30½, erit hic numerus diametrorum terrestrium qui continentur recta LT quae est distantia lunae a terra.

5) En 1688 Huygens évalua avec Cassini, d'après les observation de celui-ci, la parallaxe du soleil (‘la parallaxe’ est dit couramment, comme on sait, pour désigner ‘la parallaxe horizontale’) à 10″18‴ (voyez la p. 410 qui suit); plus tôt, en 1659, sans observation directe à environ 8″ ce qui est fort proche de la vraie valeur; voyez les p. 192, 347 (note 7) et 378 du T. XV. ou bien la p. 308 qui suit Consultez aussi sur la vraie valeur la note 7 de la p. 397 du T. XIX.

F bis.
P. 101. Pour trouver combien la refraction de l'atmosphere eleve le soleil.

Vide figuram paginae praecedentis [Fig. 4].

Posons en premier lieu que le soleil n'a point de parallaxe sensible, comme l'on l'a assez reconnu par l'experience. .... Etc. C'est le brouillon de la première partie du § 8 de la p. 31 qui précède.

F ter.
P. 101.

Pour trouver la mesme chose sans l'aide d'une horloge a pendule ... Etc. C'est le brouillon de la deuxième partie du § 8. Huygens ajoute: Mais la premiere maniere est meilleure et plus facile.

H.
P. 107. Maniere pour trouuer les lieux des estoiles fixes par le moyen d'une horloge a pendule et des filets, comme aussi leur refraction.

2 Nov. 1666.

Premierement pour trouuer les differences des Ascensions droites l'on n'aura qu'a suspendre deux filets avec des poids en bas. .... Etc. C'est le brouillon du § 5 de la p. 28 qui précède. Nous avons observé à la p. 28 que le § 5 semble être antérieur en date au § 4, et en effet dans le Manuscrit C le brouillon du § 5 précède celui du § 4.

Ce ‘§ 5’, nous l'avons dit dans l'Avertissement, correspond au ‘§ 5’ latin de la p. 529 du T. XV. Le brouillon H correspond presque mot à mot avec la Pièce lue à l'Académie.