Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 421]
| |||||
III. A Paris (juillet 1671 - juillet 1676)III, 1. Question des signes dans les equations de géométrie analytiqueGa naar voetnoot1).
| |||||
[pagina 422]
| |||||
III, 2. Trois problèmes sur le triangle.
| |||||
[pagina 423]
| |||||
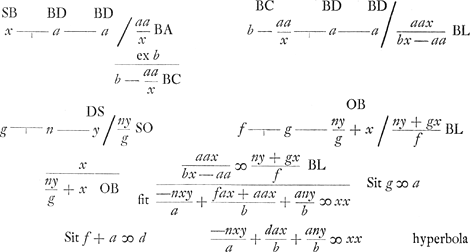 Quia igitur locus puncti D est hyperbola data, ejusdemque puncti D locus est circumferentia data MDN, erit ad intersectionem utriusque. Si angulus ABC rectus, erunt termini in quibus g infinite parvi, ideoque tunc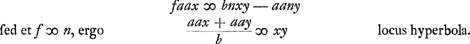 Remarque ajoutée plus tard: Ao 1680. Facto examine per regulam in libro E traditam, invenitur problema planum esse, quia nempe regula ostendit punctum B esse in axe hyperbolaeGa naar voetnoot5).  [Fig. 69]
Aliter [Fig. 69]. Super recta AK, radio AK ∞ b summae laterum, describatur arcus KE, in quo quaeratur punctum E, ut ducta AE, et intra angulum EAK accommodata perpendiculari BD ∞ a, positaque BC∞ BE, fiat triangulum ABC quod quaeritur. Sit EH | |||||
[pagina 424]
| |||||
perpend. AK. et AH ∞ x, HE ∞ y, reliqua construantur ut prius. 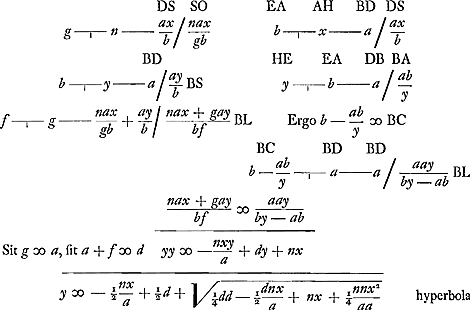 Constructio problematis folij praeced. 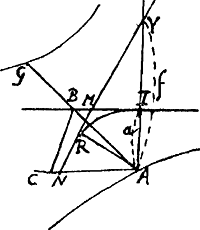 [Fig. 70]
Angulus datus IAR [Fig. 70]. Perpendic. AR ∞ AI. RY perpend. AR. AC perpend. AI. IM parall. AC. IM, MY sunt asymptoti. Hyperbola transit per A, altera opposit [arum sectionum]. AG ∞ summae laterum. AG secat hyperbolam. BC ∞ BG. Triang. ABC quaesitum. 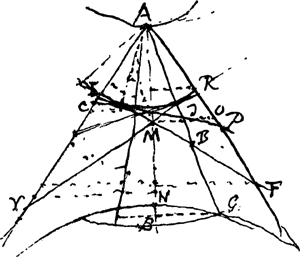 [Fig. 71]
Melius. [Fig. 71]. Sit angulus datus CAR, perpendicularis data ∞ AI vel AR. Summa laterum AG. Sit IF perpend. AI. Et RY perpend. AR. Intersectio in M est cen- | |||||
[pagina 425]
| |||||
trum oppositarum sectionum. Asymptoti RY, IF. A puncto in hyperbola cui opposita NG (scilicet sumpta MN ∞ MA) secabit circumf. radio AG descripram in G. Eritque ductâ AG quae secat IF in B, alterum latus trianguli quaesiti AB, alterum BG. Sumtisque AP ∞ AB, et AC ∞ BG, junctâque CP, erit ipsum triangulum CAP. Cum centrum circumfae. sit in axe hyperbolae constat hinc problema esse planumGa naar voetnoot6).  | |||||
BGa naar voetnoot7).Couper un triangle donnè ABC [Fig. 72] en 4 parties egales par deux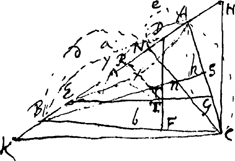 lignes qui se coupent a angles droits. AB ∞ a, BC ∞ b, AC ∞ h, BN ∞ d, NA ∞ e. AE ∞ x, DB ∞ y [CN = n. CN ⫟ AB. CK//GE. CH//FD.] 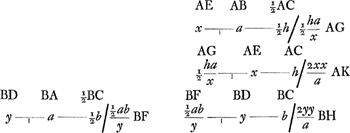 | |||||
[pagina 426]
| |||||
 | |||||
[pagina 427]
| |||||
Haec una aequatio. Jam inventio alterius sequitur considerando sectionem fieri ad angulos rectos.  Videndum quae natura curvae hujus loci. Posant x ∞ y, Huygens tire de sa première équation 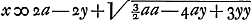 la valeur y ∞ ⅚a. Substituant cette valeur de x et de y dans sa deuxième équation, où e = d = ½a, il obtient 162hh + 162bb ∞ 337aa. la valeur y ∞ ⅚a. Substituant cette valeur de x et de y dans sa deuxième équation, où e = d = ½a, il obtient 162hh + 162bb ∞ 337aa.
Sit h ∞ b ad inveniendum quantitatem rectae quae ab angulo verticis ad mediam basin ducitur. 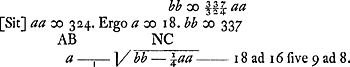 | |||||
[pagina 428]
| |||||
Quand dans un triangle la raison de AB a NC qui est menee de l'angle opposè au point de bisection de la base AB est de 9 à 8, l'on aura les points D et E dont il faut mener les lignes cherchees DF, EG, en prenant AD et BE chacune ⅙ de AB. Car en menant DF, EG en sorte qu'elles coupent chacune le triangle en 2 parties egales, elles se couperont a angles droits et diviseront le triangle en 4 parties egales. Ce cas a estè remarquè par M. Maubuisson.
Nous observons (voyez sur ce sujet le dernier alinéa de la note 8) que les calculs de Huygens qui précèdent ne démontrent ce théorème plus général de Maubuisson que dans le cas où le triangle est isoscèle. Avant de supposer AC = BC, Huygens avait déjà pris dans la Fig. 72 NC comme une perpendiculaire à la base AB et non pas comme la droite ‘menee de l'angle opposè au point de bisection de la base’Ga naar voetnoot8).  | |||||
[pagina 429]
| |||||
C'est une autre forme de la deuxième équation trouvée plus haut; Huygens observe: Nota quod nn - ed ∞ bb + hh - aa/2 sive qu. NC - ▭ 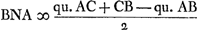 . .
Ex prima aequatione concursus linearum x et y super rectis AB, AC [Fig. 73] perpendiculariter ductarum est ad hyperbolam VHV quae eadem manet manente basi trianguli AB [Fig. 72 et Fig. 73]Ga naar voetnoot9). Ex altera vero aequatione concursus ejus punc- 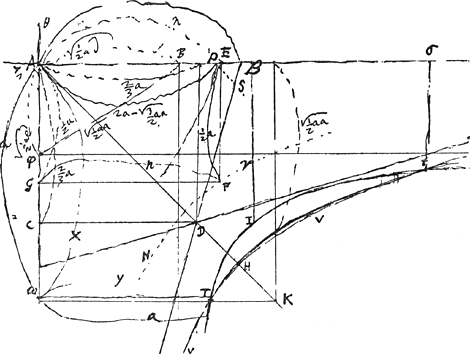 [Fig. 73]
| |||||
[pagina 430]
| |||||
tum est ad curvam TI, quae describitur ope hyperbolae FN cujus rectangulum habet latera ½a et n. Nam sumpta Aw ∞ x ad arbitrium, auferaturà quo. Aω qu. Aφ ∞ ½ae et residui radici sit aequalis Aβ, et applicetur βγ ad hyperbolam FN. Et addatur quo. βγ qu. AB ∞ ½ad, summae radix erit ωT ∞ y. Ita enim ▭ sub
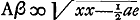 et sub et sub
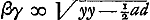 erit aequale ½an sive AF.
Jam intersectio igitur hyperbolae HV et curvae TI indicabit y ∞ T ω, et x ∞ ω A. Debet autem intersectio cadere intra quadratum AK cujus latera ∞ a basi dati trianguli, quia nec x nec y possunt excedere ipsam basin. quod si extra cadat, indicio est sectionis puncta utraque non cadere in illam basin, sed in alterum e lateribus. Dans la Fig. 75 p.e. le point D tombe sur le prolongement de la base BA et le point G sur le prolongement du côté AC pour l'une des erit aequale ½an sive AF.
Jam intersectio igitur hyperbolae HV et curvae TI indicabit y ∞ T ω, et x ∞ ω A. Debet autem intersectio cadere intra quadratum AK cujus latera ∞ a basi dati trianguli, quia nec x nec y possunt excedere ipsam basin. quod si extra cadat, indicio est sectionis puncta utraque non cadere in illam basin, sed in alterum e lateribus. Dans la Fig. 75 p.e. le point D tombe sur le prolongement de la base BA et le point G sur le prolongement du côté AC pour l'une des
 [Fig. 75]
deux manières de diviser le triangle ABC en quatre parties égales par les droites perpendiculaires entr'elles DF et EG.
Ob aequationem xxyy ∞ ½adxx + ½aeyy - ¼aade + ¼aann videtur curva ex quatuor lineis constare quarum hic una descripta est, reliquae similes huic in angulis BAϑ, CAζ, ϑAB sint describendae. Potest enim eadem existere aequatio sive sumantur + x et + y, sive - x et - y, sive + x et - y, sive - x et + y. Sed tres reliquae hic inutiles videntur quia in altera aequatione ad hyperbolam non possunt mutarisigna affectio nis x nec y, ut maneat eadem aequatio. Ergo hic ea tantum intersectio utilis quae cadit intra quadrantem AK, (cadit autem nonnunquam utraque) et quae extra ut hic t, ita solvit problema ut satisfiat postulatis quae in analysi consideravimus, nempe ut [Fig. 72] ▭ sub EA, AG sit ∞ ½ ▭ sub BA, AC, et ▭ EDT ∞ ½ ▭ BDF et anguli ad T recti. | |||||
[pagina 431]
| |||||
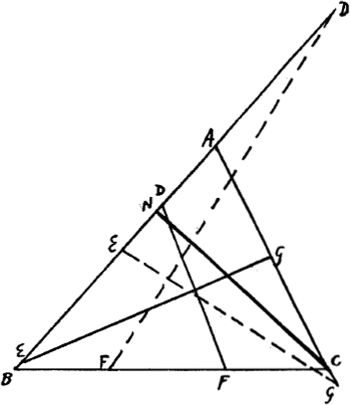
CGa naar voetnoot10). Data base trianguli AB ∞ a [Fig. 76] angulo ad basin BAC et rectangulo
 [Fig. 76]
a lateribus ACB, invenire triangulum. CG perpend. AB. Ratio CG ad GA et ad CA data est, sit CG ad GA ut a ad b, et CG ad CA ut a ad c. 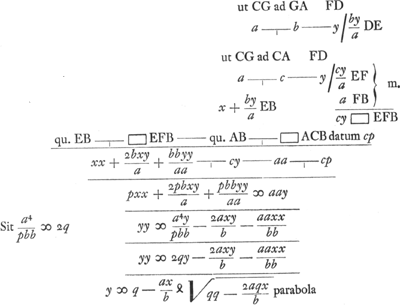 Constructio. Angulus datus BAQ [Fig. 77]. BQ perpend. AB. Ut AR, p ad BQ, aa/b ita haec ad aliam a4/pbb ∞ 2q cujus dimidium BI ∞ q. IL parallela AC, IM ∞ ½IL. M est vertex parabolae. BS perpend. IL. IS ∞ aq/c, ½ latus rectum. Diameter parabolae MI. F intersectio parabolae et circumferentiae centro B radio BA descriptae. BF recta secans AQ in C. Triangulum quaesitum est ACB. Parabola transit per punctum B. 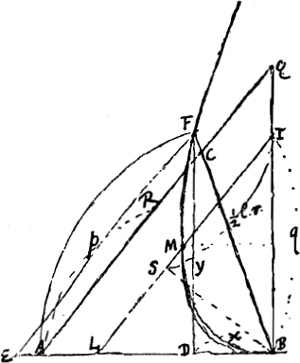 [Fig. 77]
| |||||
[pagina 432]
| |||||
III, 3.Ga naar voetnoot1) Un théorème sur la tangente à l'ellipse.
| |||||
[pagina 433]
| |||||
III, 4Ga naar voetnoot1) Un problème sur le quadrilatère, avec extension du théorème trouvé en cette occasion sur le quadrilatère inscrit dans une circonference de cercle, à un polygone inscrit quelconque.
| |||||
[pagina 434]
| |||||
Sed quia habetur sszz + ttzz estque ss + tt ∞ 2bb + 2cc ut facile apparet, erit quadr. areae trianguli 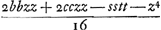 vel si bb + cc dicatur oo, et st sive bb - cc dicatur gg, Erit quadr. areae triang.i vel si bb + cc dicatur oo, et st sive bb - cc dicatur gg, Erit quadr. areae triang.i 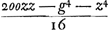 . .
adeo ut regula etiam hoc modo possit enunciari. Summa quadratorum duorum laterum ducatur in quadratum lateris reliqui, et à producti duplo auferatur quadratum differentiae quadratorum duorum priorum laterum, una cum quadratoquadrato lateris reliqui. Residui pars decimasexta erit aequalis quadrato areae trianguli. Sit jam trapezium cujus latera AB ∞ b; BC ∞ c, AD ∞ a, DC ∞ d. Area trapezij ∞ ee [Fig. 79]. 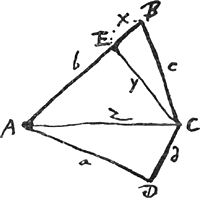 [Fig. 79]
Ducta CE perpend.i in AB sit BE ∞ x, EC ∞ y ut punctum C terminus lateris BC, si potest, ad locum redigatur; cujus intersectio cum circumferentia centro B radio BC descripta dabit determinationem puncti C; adeoque constructionem problematis. Sit bb + cc ∞ oo; bb - cc ∞ gg; aa + dd ∞ hh; aa - dd ∞ ff. Et ducatur diagonius AC ∞ z. Erit igitur area triang.i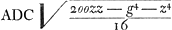 Ga naar voetnoot3) ex regula praemissa. addatur area ∆i ABC ∞ ½by, area trapez. Ga naar voetnoot3) ex regula praemissa. addatur area ∆i ABC ∞ ½by, area trapez.
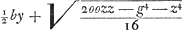 Ga naar voetnoot3) ∞ ee. aequatio pag. praec. Ga naar voetnoot3) ∞ ee. aequatio pag. praec.
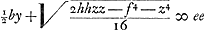 Ga naar voetnoot4) Ga naar voetnoot4) 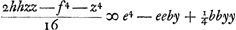 sed yy ∞ cc - xx sed yy ∞ cc - xx
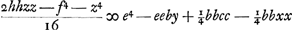
Atqui zz ∞ bb + cc - 2bx ex Euclide. Sive zz ∞ oo - 2bx quia bb + cc ∞ oo. | |||||
[pagina 435]
| |||||
 Est ergo locus puncti C linea recta. Eritque Constructio problematis hujusmodi. Sit BF [Fig. 80] perpend. ad AB. ipsaque BF aequalis sumatur  [Fig. 80]
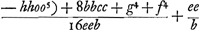 Ga naar voetnoot5) ductaque FG parall. BA et in eandem partem quo tendit BA, sit FG ad ipsi perpendicularem GH, ut 4ee ad hh - oo, sumptâ GH in consequentia punctorum BF si hh majus quam oo, at in partem contrariam si hh minus quam ooGa naar voetnoot6). deinde ducatur FH eamque secet circumf.a radio BC ∞ c, descripta centro B. Intersectio definiet locum puncti C, unde constructio reliqua manifesta est. Ga naar voetnoot5) ductaque FG parall. BA et in eandem partem quo tendit BA, sit FG ad ipsi perpendicularem GH, ut 4ee ad hh - oo, sumptâ GH in consequentia punctorum BF si hh majus quam oo, at in partem contrariam si hh minus quam ooGa naar voetnoot6). deinde ducatur FH eamque secet circumf.a radio BC ∞ c, descripta centro B. Intersectio definiet locum puncti C, unde constructio reliqua manifesta est.
NB. debet BF sumi in partem contrariam si in quantitatibus ipsam BF denotantibus praevaleant signata per -. Hic jam nunc patetGa naar voetnoot7) quod cum circulus CC tangit FH, hoc est cum area maxima, tunc EC ad EB, ut FG ad GH, hoc est ut 4ee ad hh - oo. | |||||
[pagina 436]
| |||||
Cum autem circumferentia secet rectam FH in duobus punctis, duplicem solutionem habebit problema, sed sciendum non semper duobus modis construi posse trapezium ex summa duorum triangulorum ABC, ADC constans, quod dato spatio aequale sit, sed nonnunquam alterum ex summa alterum ex differentia horum triangulorum constitui; quod inde fit quia in prima aequatione, ubi 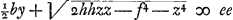 , non referat utrum radix habeat signum + an -, hoc est an summa an differentia triangulorum aequetur areae datae ee; quia ducendo in se , non referat utrum radix habeat signum + an -, hoc est an summa an differentia triangulorum aequetur areae datae ee; quia ducendo in se 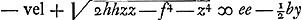 , semper ijdem plane termini orientur. , semper ijdem plane termini orientur.
Estautem limitatio haec, quod si area data major sit quam triangulum ex lateribus AB, BC, et reliquis AD, DC in unam rectam extentis effectumGa naar voetnoot8), tunc dupliciter construi poterit trapezium ex summa triangulorumGa naar voetnoot9). Si vero minor dicto triangulo sit area data, tunc vel nullum vel unum tantummodo hujusmodi trapezium ex summa construi poterit, eritque alterum ipsi aequale ex differentia triangulorum ABC, ADC. AliquandoGa naar voetnoot10) nullum nec ex differentia construi poterit. Quod si circumferentia tangat rectam FH, ducta BC ad punctum contactus, efficietur trapezium omnium quae fieri possunt maximum. Ad inveniendam autem determinationem areae maximae quae datis quatuor lateribus comprehendi possit, repetatur aequatio ultimo reperta, sed brevitatis gratia scribatur,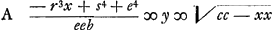 ; ponendo nempe 4hhb - 4oob/16ee ∞ - r3/ee sive hhb - oob/4 ∞ - r3; et - 2hhoo + g4 + 8bbcc + f4/16 ∞ s4. ; ponendo nempe 4hhb - 4oob/16ee ∞ - r3/ee sive hhb - oob/4 ∞ - r3; et - 2hhoo + g4 + 8bbcc + f4/16 ∞ s4.
| |||||
[pagina 437]
| |||||
quadrando utrinque fiet  CurGa naar voetnoot12) non possumus hinc invenire quod x jam 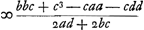 ? ut revera est, aequè ac cum circulo inscribitur trapezium ut inventum est pagina 2Ga naar voetnoot13).
NB.Ga naar voetnoot14) esse hic x ad y sicut r3 ad bee hoc est ut ? ut revera est, aequè ac cum circulo inscribitur trapezium ut inventum est pagina 2Ga naar voetnoot13).
NB.Ga naar voetnoot14) esse hic x ad y sicut r3 ad bee hoc est ut 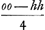 ad ee. Hoc ostendendum esset ita quoque se habere cum trapezium est in circulo. tunc enim regula inde existeret, quae fol. sequ. in fine habetur, ad inveniendam aream trapezij in circulo. ad ee. Hoc ostendendum esset ita quoque se habere cum trapezium est in circulo. tunc enim regula inde existeret, quae fol. sequ. in fine habetur, ad inveniendam aream trapezij in circulo.
Si valor x restituatur in aequatione B, habebitur area ee maxima determinata per latera trapezij data, sed fiet aequatio in qua e12, e8, e4. quae non facile divisibilis cognoscetur etsi revera sit divisibilis. Et licet jam reducta ponatur, nondum constabit an trapezium omnium maximum sit illud quod in circulo inscribatur. Quod hac via itaque inquirere institui.  [Fig. 81]
Si trapezium ABCD [Fig. 81] est in circulo; positis nominibus laterum ut supra, et area ee, ductaque perpend.i CE ∞ y: si porro ducatur perpend. AQ in latus productum CD, erit AQ ∞ ay/c quia triang.a CBE, ADQ sunt similia, ut facile apparet. 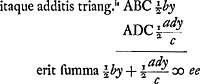 | |||||
[pagina 438]
| |||||
Ergo cum trapezium est in circule fit 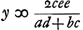 , non tamen cum haec aequalia trapezium est in circulo, quia non consideravi basin communem esse AC.
Cum vero trapezium est maximum fit , non tamen cum haec aequalia trapezium est in circulo, quia non consideravi basin communem esse AC.
Cum vero trapezium est maximum fit 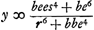 .
Sit igitur oportet .
Sit igitur oportet 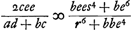 , unde , unde 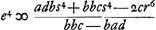 .
Quod si jam haec aequatio sit regula ad inveniendam aream trapezij circulo inscripti; concludam inde idem trapezium circulo inscriptum esse maximum. Si enim, cum trapezium est in circulo, fit e4 ∞ adbs4 &c. hoc est, .
Quod si jam haec aequatio sit regula ad inveniendam aream trapezij circulo inscripti; concludam inde idem trapezium circulo inscriptum esse maximum. Si enim, cum trapezium est in circulo, fit e4 ∞ adbs4 &c. hoc est, 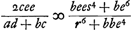 ; estautem, cum trapezium in circulo, ; estautem, cum trapezium in circulo,  . Ergo, cum trapezium in circulo, erit et . Ergo, cum trapezium in circulo, erit et 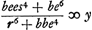 ; hoc autem cum fit, efficitur trapezium maximum. Ergo, cum trapezium in circulo, fiet trapezium maximum. Restat itaque examinandum an aequatio ultimo inventa contineat regulam ad inveniendam aream trapezij in circulo. Quod quidem ita se habere comperi. Nam restituto primum valore r3 et s4, secundum ea quibus aequalia posita fuere, ac deinde restituto etiam valore hh, oo, ff et gg, invenitur divisionem fieri posse per bc - ad, et fit ; hoc autem cum fit, efficitur trapezium maximum. Ergo, cum trapezium in circulo, fiet trapezium maximum. Restat itaque examinandum an aequatio ultimo inventa contineat regulam ad inveniendam aream trapezij in circulo. Quod quidem ita se habere comperi. Nam restituto primum valore r3 et s4, secundum ea quibus aequalia posita fuere, ac deinde restituto etiam valore hh, oo, ff et gg, invenitur divisionem fieri posse per bc - ad, et fit 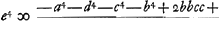 Ga naar voetnoot15). Et rursus abbreviando 16e4 ∞ 2hhoo - f4 - g4 + 8adbcGa naar voetnoot16). Ga naar voetnoot15). Et rursus abbreviando 16e4 ∞ 2hhoo - f4 - g4 + 8adbcGa naar voetnoot16).
Sed quia f4 ∞ h4 - 4aadd et g4 ∞ o4 - 4bbcc, ut facile colligitur quia bb + cc ∞ oo; bb - cc ∞ gg; aa + dd ∞ hh; aa - dd ∞ ff, fit 16e4 ∞ 2hhoo - h4 - o4 + 4aadd + 4bbcc + 8adbc. 16e4 ∞ - qu. hh - oo + qu. 2ad + 2bc. ConvenitGa naar voetnoot17) cum Regula qua invenitur area trapezij in Circulo. quae regula reperitur pag. versaGa naar voetnoot18). 16e4 - ∞ - qu. aa + dd - bb - cc + qu. 2ad + 2bc, ut autem habeatur differentia quadratorum ab his radicibus, multiplicetur summa radicum in ipsarum differentiam, hoc est aa + 2ad + dd - bb + 2bc - cc in bb + 2bc + cc - aa + 2ad - dd ∞ 16e4. | |||||
[pagina 439]
| |||||
Quum igitur haec regula sit ad inveniendam aream trapezij circulo inscripti, eadem regula erit ad inveniendam aream maximi trapezij ex quatuor datis lateribus. Nempe
A quadrato summae quorumlibet duorum laterum auferatur quadratum differentiae duorum laterum reliquorum; et vicissim a quadrato summae horum auferatur quadratum differentiae illorum. duo residua in se ducta dabunt quadratum areae trapezij maximi sexdecuplum.
Vel addantur omnia trapezij latera; à summae dimidio auferantur latera singula; residua quatuor in se ducantur, erit producti radix qu. aequalis areae trapezijGa naar voetnoot19).
Hinc facile demonstratur polygonum quodvis, inaequalium licet laterum, circulo inscriptum maximum esse omnium quod ex ijfdem lateribus eodem vel alio quocunqueGa naar voetnoot20) ordine connexis confici possitGa naar voetnoot21).
Trapezij circulo inscripti aream invenire. 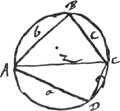 [Fig. 82]
∆ ABC [Fig. 82] secundum Regulam inventam superius ubi de hac quaestione 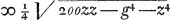 Ga naar voetnoot22). Ga naar voetnoot22).
bc [ad] ad [ut] ∆ ABC ad ∆ ADC. zz ∞ ooad + hhbc/ad + bc secundum regulam inventu facillimamGa naar voetnoot23). | |||||
[pagina 440]
| |||||
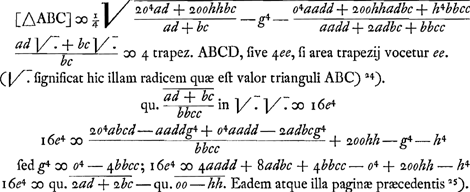 Ga naar voetnoot24)Ga naar voetnoot25) La méthode dont Huygens se sert dans la solution de ce problème est désignée par lui, à la p. 47 du Manuscrit E, par les mots Methodus nostra. La p. 46 donnait la Methodus Romeri. Les côtés étant √a, √b, √c, √d, l'aire e et la diagonale cherchée √x [Fig. 83], Roemer écrit: 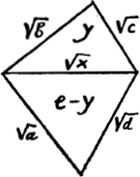 [Fig. 83]
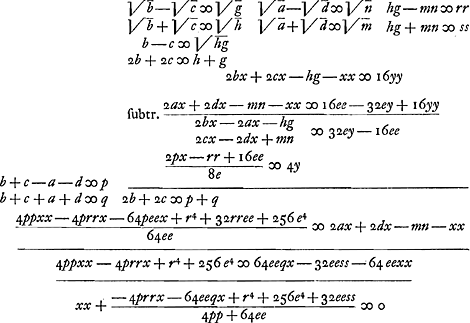 Voyez aussi aux p. 80-81 du T. VIII une solution de A. Monforte, reçue par Huygens en 1678. | |||||
[pagina 441]
| |||||
III, 5Ga naar voetnoot1). Les ‘Quantitez imaginaires’.
|
| xx + 4x + 10 { x + 2 - √ - 6 | |
| xx + 4x + 10 { x + 2 + √ - 6 | Etc. |
On trouve à la p. 58 du Manuscrit E la date 8 Dec. 1675. Quant à la p. 53Ga naar voetnoot1) elle contient aussi le sommaire de la lettre du 30 septembre de Huygens à Leibniz. Nous avons publié ce sommaire, traitant e.a. des quantitez imaginaires, ainsi que la lettre, aux p. 504 et suiv. du T. VII, où l'on voit qu'on a cru devoir dater cette lettre du 30 septembre 1675. Huygens dit dans la lettre avoir este fort longtemps hors d'exercice pour ce qui regarde [les] Equations Algebraiques [considérées]. Il ne se sent apparemment pas porté à poursuivre sérieusement l'étude des quantités imaginaires, ce qui ressort aussi plus ou moins de la plaisanterie sur les racines des équations algébriques en général par laquelle se termine le sommaire.
- voetnoot1)
- Manuscrit D, p. 308, avril 1672.
- voetnoot2)
- Manuscrit D, p. 420-425, août, septembre ou octobre 1673. Ces pages suivent celles (p. 418-419) où Huygens traite de la ‘Problematis Alhazeni analysis brevissima’ (comparez le début de l'Appendice II à la p. 330 qui précède); ce sont surtout les solutions de ce problème qui le familiarisèrent avec les équations du deuxième degré représentant des hyperboles.
Il avait d'ailleurs déjà considéré le même problème vers la fin de 1668 (Manuscrit D, p. 113 et suiv.).
- voetnoot3)
- Voyez la p. 410 du T. VII où Huygens dit avoir visité M. de Maubuisson, qui ne nous est pas connu autrement, en janvier 1675.
- voetnoot2)
- Manuscrit D, p. 420-425, août, septembre ou octobre 1673. Ces pages suivent celles (p. 418-419) où Huygens traite de la ‘Problematis Alhazeni analysis brevissima’ (comparez le début de l'Appendice II à la p. 330 qui précède); ce sont surtout les solutions de ce problème qui le familiarisèrent avec les équations du deuxième degré représentant des hyperboles.
Il avait d'ailleurs déjà considéré le même problème vers la fin de 1668 (Manuscrit D, p. 113 et suiv.).
- voetnoot4)
- Voyez la note 6 de la p. 425 qui suit.
- voetnoot5)
- Voyez la note suivante. Huygens entend sans doute parler des considérations sur l'équation de l'hyperbole qu'on trouve à la p. 14 du Manuscrit E (‘si haec proportionalia, problema erit planum’).
- voetnoot6)
- Ailleurs (Chartae mathematicae, f. 139, voyez sur cette feuille la note suivante) Huygens écrit de même: Problema Pappi apparet hinc planum esse quod centrum circuli BE cadat in axem hyperbolae OA.
Voyez sur Pappus et les problèmes plans les p. 15-16, 213 et 240 du T. XI, 7, 82 et 107-108 du T. XII, et 421 du T. XIV.
- voetnoot7)
- Chartae mathematicae, f. 139 et Manuscrit D p. 427-433 et 435-436, août, septembre ou octobre 1673. La Fig. 72 est empruntée à la f. 139 nommée, qui doit avoir fait partie du Manuscrit D: les calculs de la p. 427 se rapportent à cette figure. Deux feuillets qui précédaient la p. 427 du Manuscrit D ont été coupés. À la p. 427 Huygens écrit inventum pag. praeced. à propos d'une certaine équation de la f. 139. Nous remarquons encore qu'on voit dans la f. 139 nommée le même filigrane que dans les feuillets 429-430 et 433-434 (et beaucoup d'autres feuillets) du Manuscrit D.
- voetnoot8)
- Une feuille séparée qui se trouve dans le Manuscrit D contient encore la figure 74 et quelques équations qui ne sont pas de la main de Huygens, non plus que les lettres de la figure. Est-ce la main de Maubuisson? Cela semble probable.

Une de ces équations (à laquelle satisfait x = ⅚a lorsque y = x) xx ‖ 8ay + 8ax - 4yx - 10aa - yy (où ‖ désigne l'égalité des deux membres) correspond à la première équation de Huygens xx ∞ 4ax - 4xy + 4ay - yy 5/2aa, lorsqu'on y change a en 2a. On trouve en effet sur la feuille les indications BF ‖ x, CE ‖ y, BC ‖ 2a [Fig. 74], tandis que chez Huygens [Fig. 72] le côté BA qui correspond à BC de la Fig. 74 était égal à a.
Huygens y a ajouté ce qui suit: BC bifariam in Q. Ratio BC in QA ut 9 ad 8. Sumantur BF et CE mediae proportionales inter BQ et BQ + QA. fiunt singulae BE, FC ∞ ⅙ BC.
Nous ignorons si Huygens a remarqué qu'on peut passer du cas considéré par lui au cas plus général considéré par Maubuisson en projetant son triangle isoscèle sur un plan quelconque parallèle à l'une des deux sécantes orthogonales entr'elles considérées qui divisent le triangle isoscèle en quatre parties égales. En effet le rapport entre la base et la médiane correspondante, qui était de 9 à 8, reste le même après la projection puisque ces deux lignes font l'une et l'autre dans le triangle isoscèle des angles de 45o avec les sécantes. Il résulte de cette démonstration, ce qui n'est pas de toute évidence dans la Fig. 74, que dans le cas considéré par Maubuisson les sécantes orthogonales se coupent toujours sur la médiane et sont toujours parallèles aux bissectrices des angles Q.
- voetnoot9)
- Puisque cette première équation, celle de l'hyperbole, ne contient d'autre paramètre que a.
- voetnoot10)
- Manuscrit E, p. 14-15, datant probablement de la fin de 1674 (la p. 26 porte la date du 19 Dec. 1674).
- voetnoot1)
- Manuscrit E, p. 29, décembre 1674 ou janvier 1675.
- voetnoot1)
- Manuscrit E, p. 44-50, juillet, aoùt ou septembre 1675 (voyez sur cette date la note 1 de la p. 441 qui suit), et Chartae mathematicae, f. 91-93. Après la p. 50 du Manuscrit E six feuillets ont été coupés. Les trois ou quatre premiers sont évidemment les f. 91-93 des Chartae mathematicae (l'une des feuilles est composée de deux feuillets collés l'un sur l'autre): on trouve sur leurs premières pages les nos 3, 4, 5 de la main de Huygens, tandis que les p. 49 et 50 du Manuscrit E portent les nos 1 et 2. Nous publions le texte des Chartae mathematicae; voyez sur celui du Manuscrit E la note 13 de la p. 437 et la fin de la p. 440.
Il s'agit ici d'un problème déjà posé et résolu en 1661 par G. Schott: voyez la p. 435 de notre T. III. Cette pièce n'avait pas été envoyée directement à Huygens, puisque la lettre de Schott (T. III, no 938) n'était pas adressée à Huygens mais à Vegelin van Claerbergen (voyez, à la p. 582 du T. IV, les Additions et Corrections au T. III). Ce dernier doit l'avoir envoyée à Huygens avec la lettre. Les p. 732-738 du T. X font voir que Huygens était en correspondance avec Vegelin van Claerbergen quoique les lettres échangées ne se trouvent pas dans la collection-Huygens de Leiden. En 1676 Huygens ne fait aucune allusion à la solution de Schott, meis il mentionne celle de Roemer (440 qui suit).
Le mot ‘trapezium’ a le sens général de quadrilatère quelconque.
- voetnoot2)
- Comparez les p. 69-71 du T. XII.
- voetnoot3)
- Lisez:
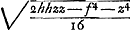 .
.
- voetnoot3)
- Lisez:
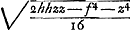
- voetnoot4)
- Il s'agit de l'équation précédente à laquelle Huygens donne maintenant la forme exacte. Dès lors Huygens procède à l'élimination de la variable z.
- voetnoot5)
- Lisez 2hhoo.
- voetnoot6)
- C'est le cas de la Fig. 80; mais cette figure montre encore les traces d'une construction antérieure où GH avait la direction de BF. Cela explique le troisième point C à droite de B qui n'appartient pas à la construction présente.
- voetnoot7)
- Cette remarque fut ajoutée plus tard.
- voetnoot8)
- Huygens suppose donc AB + BC > AD + DC, ce qui est permis, excepté dans le cas, qu'il n'est pas nécessaire de considérer, où AB = DC et AD = BC. De plus lorsque les segments a, b, c, d sont choisis de manière qu'ils peuvent constituer les côtés d'un quadrilatère on aura (supposant AB ≧ BC) AB - BC < AC < AD + DC. La construction du triangle en question est donc toujours possible.
- voetnoot9)
- Commençant par sa valeur maximale, lorsque le quadrilatère devient inscriptible au cercle, on peut diminuer graduellement l'aire donnée. Évidemment les deux quadrilatères seront alors au début égaux à la somme des triangles ABC, ADC et la transition aux autres cas ne peut arriver qu'à l'instant où l'aire de l'un de ces triangles s'annule. Toutefois cela peut toujours arriver de deux manières différentes, savoir celle envisagée par Huygens, où AC devient égale à la somme de AD et DC et, en outre, dans le cas où la différence de AB et BC est plus petite que la différence de AD et DC, celle où AC devient égale à la différence de AD et DC, ou, dans le cas contraire, celle où AC est égale à la différence de AB et BC, auxquels cas c'est l'aire du triangle ABC qui s'annule. Or, il dépend de la grandeur relative des triangles qui restent laquelle de ces manières se présentera la première. Si c'est celle de Huygens sa conclusion est juste; si c'est l'autre, elle doit être modifiée.
- voetnoot10)
- Cette phrase fut ajoutée plus tard.
- voetnoot11)
- Il s'agit d'une application de la méthode de Hudde exposée dans son ‘Epistola secunda de maximis et minimis’ qui fut publiée par van Schooten p. 507-515 de l'édition de 1659 de la ‘Geometria’ de Descartes, Elle est basée sur la considération que pour la valeur maximale de e l'équation en x aura des racines égales. Comparez la Pièce II qui précède (p. 223 et suiv.).
- voetnoot12)
- Cette phrase fut ajoutée plus tard.
- voetnoot13)
- C'est la p. 50 du Manuscrit E (comparez la note 1 de la p. 433). Le raisonnement de Huygens, appliqué à la Fig. 81, revient à ce qui suit. On a QD = a/c. BE = ax/c, et ensuite
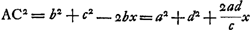 ; équation qui conduit à l'expression désirée.
; équation qui conduit à l'expression désirée.
- voetnoot14)
- Cet alinéa a été ajouté plus tard.
- voetnoot15)
- Ajoutez au numérateur: + 2aabb. Nous avons vérifié ce résultat.
- voetnoot16)
- Cette réduction implique l'addition indiquée dans la note précédente.
- voetnoot17)
- Cette phrase fut ajoutée plus tard.
- voetnoot18)
- Voir la page suivante.
- voetnoot19)
- Cette règle aujourd'hui si bien connue avait été donnée par Snellius sans démonstration sous la forme: ‘Si de dimidio collectorum laterum dati quadranguli in circulum inscripti latera sigillatim subducantur, latus continue à quatuor differentijs facti erit area’; voir la p. 139 de l'ouvrage: ‘Ludolphi à Ceulen De circulo & adscriptis liber. In quo plurimorum polygonorum latera per irrationalium numerorum griphos, quorum libet autem per numeros absolutos secundum Algebricorum aequationum leges explicantur. Quae insuper accesserunt pagina versa indicabit. Omnia é vernaculo Latina fecit, & annotationibus illustravit Willebrordus Snellius R.F. Lugd. Batav. Apud Iodocum Colster Anno 1619’.
On a découvert plus tard que la même règle avait déjà été formulée par le mathématicien hindou Brahmagupta qui vivait au septième siècle.
- voetnoot20)
- Ces trois mots furent ajoutés plus tard.
- voetnoot21)
- Si nous considérons un quadrilatère qui a pour sommets quatre sommets consécutifs A, B, C, D du polygone, son aire doit être maximum, afin qu'il en soit ainsi de l'aire du polygone. Le cercle qui passe par A, B, C doit donc passer par D; donc aussi par E, etc.
- voetnoot22)
- Voir lap. 434.
- voetnoot23)
- La règle se déduit en effet facilement des relations mentionnées dans la note 13 de la p. 437.
- voetnoot24)
- Lisez: 4 ∆ ABC.
- voetnoot25)
- Voir la p. 438.
- voetnoot1)
- Manuscrit E, p. 53. On pourrait douter (comparez la note 1 de la p. 496 du T. XVIII) si cette page est de 1675 ou bien de 1676, mais pour la raison donnée dans le texte nous adoptons la date de septembre 1675.
- voetnoot1)
- Manuscrit E, p. 97-98.


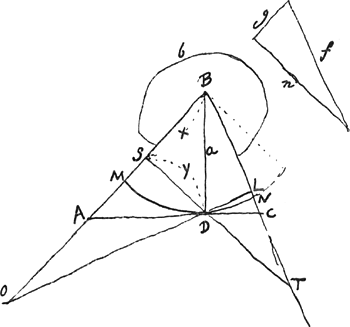

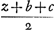 ,
, 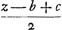 ,
, 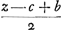 ,
, 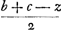 productum erit aequale quadrato areae trianguli.
productum erit aequale quadrato areae trianguli.
