Oeuvres complètes. Tome XX. Musique et mathématique

[p. 442]

IV. À La Haye (juillet 1676 - juin 1678)

IV, 1. Questions se rapportant au traité ‘Van rekeningh in spelen van geluck’.

Voyez les Pièces d'août 1676 etc. aux p. 151 et suiv. du T. XIV.

IV, 2. Question des signes dans les équations de géométrie analytique.
[1676 ou 1677]

Ponantur rectae AB, BC angulum rectum constituere. Sitque indefinite AB ∞ x [Fig. 84], BC ∞ y et a linea data. Aequatio autem curvae AC naturam exprimens²⁾ ax - xx ∞ yy sive xx - ax + yy ∞ 0.

[Fig. 84]

Hic sive ponatur + y sive - y, eadem tamen fit aequatio, unde sequitur curvam AC ejus esse naturae ut BC ∞ y ad utramvis partem rectae AB sumi possit. Estque sane circuli circumferentia cujus diameter a, ut facile apparet.

Non potest autem sumi x in contrariam quoque partem nempe versus D, quia si statuatur - x, non poterit fieri eadem priori aequatione sed erit xx + ax + yy ∞ 0. Nam in priori cum haberetur - ax, essetque + x necesse est fuisse - a. quare posito - x ductoque in - a (nam hoc non mutatur) fit + ax.

2) Quelques années plus tard Huygens parlera simplement de l'‘aequatio parabolae’ (l. 10 de la p. 408 qui précède). En 1691 il se sert couramment de l'expression ‘equation d'une courbe’; voyez la suite du Tome (p. 506 et suiv.).

[p. 443]

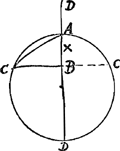
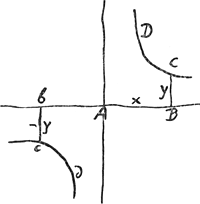
Sit item aequatio xy ∞ aa quae hyperbolae ad asymptotos relationem ostendit [Fig. 85]. Hic potest etiam - x poni sed tunc et - y ponendum, ut fiat utriusque multiplicatione

[Fig. 85]

+ xy. Itaque sumto x in contrariam partem ab A, etiam y sive be in contrariam partem a recta AB sumenda est, tuncque punctum c est ad sectionem oppositam, ut vocant, ipsi CD. Patetque aequatione proposita designari curvam ex duabus CD, cd constantem, non vero pluribus. adeo ut sectiones conjugatae non faciant partem ejus.

Sit rursus aequatio x³ ∞ aay [Fig. 86]. Hic manente + x debet etiam manere + y. at posito - x debet quoque poni - y ut fiat - x³ ∞ - aay, nam haec eadem aequatio est ac + x³ ∞ aay. Unde haec curva erit CAc, quae axem non habebit. Vocatur autem parabola cubica vel Paraboloides.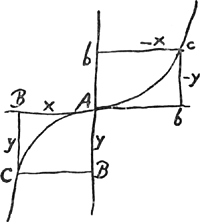

[Fig. 86]

Quod si sit aequatio x³ ∞ aay [Fig. 87]. Hic manente + x potest esse + y vel - y ut eadem maneat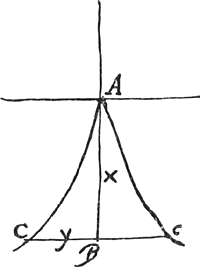

[Fig. 87]

aequatio sed non potest unquam sumi - x sive statuatur + y sive - y. Unde haec curva habebit formam CAc, angulo acutissimo ad A inflexam.