Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 382]
| |||||||
II. Une quadrature approchée du cercleGa naar voetnoot1).
| |||||||
Prop. 2.Iisdem positis dico residuorum ANBS, BFCG centrum gravitatis minus abesse à puncto D quam punctum H. Cum enim portionis parabolicae BECG centrum gravitatis sit in diametro ejus GE, centrum vero gravitatis portionis circularis BECF sit in diametro ejus EF. necesse est centrum gravitatis residui BGCF esse ad eam partem rectae EF quae versus C. Sed non potest esse extra ambitum BECF. Ergo erit intra ambitum EFC, ac proinde minus distabit a basi DC quam punctum F. Ac proinde minus utique quam punctum G vel H. Quare et recta residuorum BFCG, BNAS centra gravitatis conjungens secabit diametrum BD inter H et D. quod erat demonstrandum. | |||||||
Prop. 3.ABC [Fig. 54] circuli portio, cujus diameter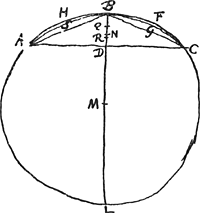 [Fig. 54]
BD. circuli centrum M, diameter BLGa naar voetnoot2). DR ∞ ⅖ BD. Per 18 nostr. de Circ. Magn.Ga naar voetnoot3) si fiat | |||||||
[pagina 383]
| |||||||
ut MR ad ⅔ DL ita BD ad aliam, ea erit altitudo trianguli majoris
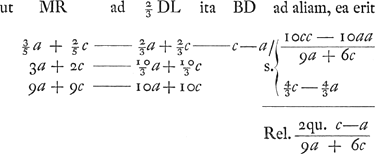 portione circ. ABC. altitudo trianguli aequalis parabolae ASBGC. majus altitudine trianguli aequalis residuo inter portiones parabolae et circuli. Jam quia 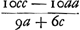 majorem rationem habet ad 4/3c - 4/3a quam portio circuli ABC ad portionem parabolae ASBGC: per conversionem rationis habebit majorem rationem habet ad 4/3c - 4/3a quam portio circuli ABC ad portionem parabolae ASBGC: per conversionem rationis habebit 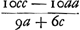 ad ad 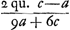 minorem rationem quam portio circuli ABC ad residuam BGCF, BSAH. Sit BQ ∞ ¼ BD. Ergo quia RD ∞ ⅖ BD, ablatis utrisque BQ et RD, quae faciunt 13/20 BD, ab BD, relinquitur QR ∞ 7/20 BD, sive 7/20c - 7/20a. Est autem Q altius quam centrum gravitatis residuorum BFCG: R vero centrum gravitatis parabolae ASBGC. Ergo QR major quam distantia inter centra gravitatis parabolae et dictorum residuorum. Quare si fiat ut minorem rationem quam portio circuli ABC ad residuam BGCF, BSAH. Sit BQ ∞ ¼ BD. Ergo quia RD ∞ ⅖ BD, ablatis utrisque BQ et RD, quae faciunt 13/20 BD, ab BD, relinquitur QR ∞ 7/20 BD, sive 7/20c - 7/20a. Est autem Q altius quam centrum gravitatis residuorum BFCG: R vero centrum gravitatis parabolae ASBGC. Ergo QR major quam distantia inter centra gravitatis parabolae et dictorum residuorum. Quare si fiat ut 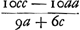 ad ad 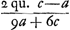 ita QR, 7/20c - 7/20a ad aliam RN ita QR, 7/20c - 7/20a ad aliam RN 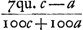 erit jam RN major quam distantia inter centra gravitatis portionis parabolicae et portionis circularis ABC. Adeoque N punctum altius centro gravitatis portionis circuli ABC. Quod si vero ad erit jam RN major quam distantia inter centra gravitatis portionis parabolicae et portionis circularis ABC. Adeoque N punctum altius centro gravitatis portionis circuli ABC. Quod si vero ad 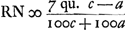 addatur DR ∞ ⅖c - ቖ a, fiet addatur DR ∞ ⅖c - ቖ a, fiet 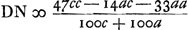 . .
| |||||||
Prop. 4.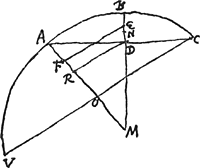 [Fig. 55]
Sit VAC [Fig. 55] circuli portio cujus diameter AO. Et ducta sit AC. Et portionis ABCD sit diameter BD. Et sumatur diametri AO pars AF ∞ ⅖ AO. ducaturque FE basi OC parallela quae diametro BD occurrat in E. Dico punctum E magis distare ab D quod basin AC bisecat quam centrum gravitatis portionis ABCD. Sit enim DR parallela EF; et concurrant productae AO, BD in M, quod erit centrum circuli VABC. Et sit MD ∞ a, MB ∞ c, AD ∞ d. | |||||||
[pagina 384]
| |||||||
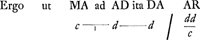 Sed quia AF ∞ ⅖ AO erit inde AF ∞ ⅘ AR, ideoque FR ∞ ⅕ AR, hoc est FR ∞ ⅕ dd/c. Ut autem RM ad MD, hoc est ut MD ad MA ita FR ad DE. 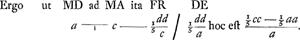 Sit jam in diametro BD inventum punctum N sicut in propositione praecedenti. altius nempe centro gravitatis portionis ABCD. Itaque cum MD sit a, MB, c, erit 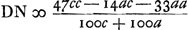 .
At DE est .
At DE est 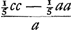 . Dico autem DN minorem esse quam DE. Si enim DN non minor quam DE, . Dico autem DN minorem esse quam DE. Si enim DN non minor quam DE,
 Atqui est minor, cum c sit major quam a. Sit enim c ∞ a + y, fit  Est igitur DN minor quam DE, ac proinde punctum E ulterius distat à basi AC quam centrum gravitatis portionis ABC, cum etiam N amplius distet. | |||||||
Prop. 5Ga naar voetnoot4).ABC [Fig. 56] portio circuli, cujus diameter BD, intra quam parabola descripta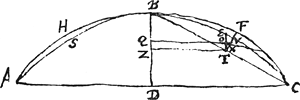 [Fig. 56]
est ASBEC. Sit BQ ∞ ⅖BD. Dico residuorum AHBS, BF CE centrum gravitatis quod est in diametro BD ulterius distare a vertice B quam punctum Q. | |||||||
[pagina 385]
| |||||||
Ducatur enim QOV parallela basi AC, et occurrat diametro portionis parabolicae BECT, quae sit TE, in O, et diametro portionis circuli BFCT, quae sit TF, in V. Et sit TZ parallela quoque AC. Quia ergo BQ ∞ ⅖ BD, hoc est ∞ ⅘ BZ, erit QZ ∞ ⅕ BZ. Sed ET propter parabolam, est dimidiae BZ aequalis. Ergo QZ ∞ ⅖ ET. Ideoque O centrum gravitatis erit portionis parabolicae BECT. Atqui recta QOV ulterius distat a basi AC quam centrum gravitatis portionis circuli BFCT. Ergo portionis hujus centrum gravitatis cadet necessario inter puncta V et T, puta in X. Et centrum gravitatis residui BFCE, cadet in recta OX producta versus X. adeoque minus distabit a basi AC quam recta VQ; eademque ratione centrum gravitatis residui AHBS. Quare utriusque centrum gravitatis commune minus distabit à basi AC sive ulterius à vertice B, quam punctum Q, quod erat demonstrandum. | |||||||
Prop. 6. [Fig. 54]
Repetatur figura prop. 3 [Fig. 54] atque etiam argumentatio eadem usque ad determinationem longitudinis BQ, quae hic ponatur ⅖ BD. Unde sic porro dicemus. RD est similiter ⅖ BD, cum R sit centrum gravitatis portionis parabolicae ASBGC. Ergo restabit QR ∞ ⅕ BD. Est autem Q altius quam centrum gravitatis residuorum AHBS, BFCG; ideoque QR major intervallo inter hoc centrum gravitatis et centrum gravitatis portionis parabolicae ASBGC. Quare si fiat ut 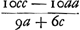 ad ad 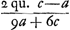 ita ita
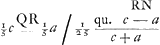 erit N punctum altius quam centrum gravitatis portionis circuli ABC.
Est autem RD ∞ ⅖ c - ⅖ a et DM ∞ a. Ideoque RM ∞ ⅖ c + ⅗ a. cui si addatur erit N punctum altius quam centrum gravitatis portionis circuli ABC.
Est autem RD ∞ ⅖ c - ⅖ a et DM ∞ a. Ideoque RM ∞ ⅖ c + ⅗ a. cui si addatur 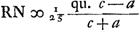 , fit , fit 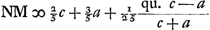 . Jam rursus per 18 de Circ. Magn. si fiat . Jam rursus per 18 de Circ. Magn. si fiat
 Haec autem ad arcuum longitudinem inveniendam transferuntur ut in prop. 19 de | |||||||
[pagina 386]
| |||||||
Circ. Magn.Ga naar voetnoot5). Adeoque si sinus arcus alicujus sit a, subtensa ejusdem c, erit arcus longitudo minor quam 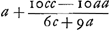 , major autem quam , major autem quam
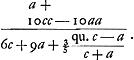
Ergo ad arcus propositi longitudinem inveniendam, fiat ut sexcupla subtensa cum noncuplo sinu, (quae linea composita vocetur N) ad summam sinus subtensaeque ita eorum differentia ad aliam, cujus decupla addatur sinui, habebiturque arcus longitudo vera major. Si vero linea N augeatur tribus quintis lineolae quae sit tertia proportionalis summae et differentiae dictae, fiet, eadem faciendo, longitudo arcus vera minor.
Quanta autem in numerorum characteribus horum terminorum possit esse differentia, simili ratione ac pag. 9 hujusGa naar voetnoot6) ostendemus. Nempe si in a et c primus characterum triens sit idem, differentia terminorum, inter quos arcus longitudo consistit, nunquam plurium quam unius erit characteris. Saepe vero ne unius quidem, sed fractio tantum cujus numerator unum, denominator quinque characteres habebit. Est enim additiuncula quae ad a apponitur, in majori termino ad eam quae in minori ut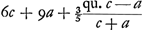 ad 6c + 9a. Ac proinde erit additiuncula major ad differentiam utriusque (quae eadem etiam terminorum est differentia) ut ad 6c + 9a. Ac proinde erit additiuncula major ad differentiam utriusque (quae eadem etiam terminorum est differentia) ut 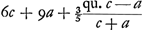 ad ad 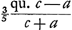 . sive ut . sive ut
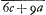 in in 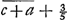 qu. c - a ad ⅗ qu. c - a
Ponatur numerus characterum similium in a et c ∞ s. Ergo tam a quam c habebit characteres 3s. atqui 6c + 9a majores sunt quam 10a. Ergo 6c + 9a habebit characteres non pauciores quam 3s + 1. Ergo et qu. c - a ad ⅗ qu. c - a
Ponatur numerus characterum similium in a et c ∞ s. Ergo tam a quam c habebit characteres 3s. atqui 6c + 9a majores sunt quam 10a. Ergo 6c + 9a habebit characteres non pauciores quam 3s + 1. Ergo et 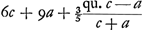 non pauciores habebit quam 3s + 1. Sed c + a non habet pauciores quam 3s. Ergo 6c + 9a in c + a, non habebit pauciores quam 6s, per theor. 1 pag. 5Ga naar voetnoot7). Rursus quia c - a non plures habet quam 2s, habebit qu. c - a non plures quam 4 s. non pauciores habebit quam 3s + 1. Sed c + a non habet pauciores quam 3s. Ergo 6c + 9a in c + a, non habebit pauciores quam 6s, per theor. 1 pag. 5Ga naar voetnoot7). Rursus quia c - a non plures habet quam 2s, habebit qu. c - a non plures quam 4 s.
Est itaque ut numerus constans characteribus non paucioribus quam 6 s ad ⅗ numeri constantis characteribus non pluribus quam 4 s, ita additiuncula major ad differentiam majoris et minoris termini. Ista vero additiuncula non est major quam 5/3 c - 5/3 a, cum | |||||||
[pagina 387]
| |||||||
vix sit major quam 4/3c - 4/3a, ideoque non plures characteres habet quam 5/3 numeri constantis non pluribus quam 2s characteribus. Ergo ad inveniendam terminorum differentiam oportet ducere ⅗ numeri non pluribus constantis characteribus quam 4s, in 5/3 numeri non plures habentis quam 2s. unde orietur numerus non pluribus constans quam 6s, cum fractiones altera alteram tollant. Et hoc productum dividendum per numerum non pauciores habentem quam 6s. unde quotiens, hoc est differentia terminorum dicta non plures uno habebit characteres. Quod si vero a initialem characterem habeat supra 5. et c - a habeat initialem 1; jam 6c + 9a in c + a habebit saltem characteres 6s + 3. Et qu. c - a non plures quam 4s - 1. eoque ducto in c - a, productum non plures quam 6s - 2: quo diviso itaque per 6s + 3, fiet fractio cujus denominator superabit numeratorem quinque characteribus, unde minor utique erit quam 1/10000. Notandum porro minorem terminum semper aliquanto accuratiorem fore majore. ut si c sit latus 60 anguli a ½ lateris 30 anguli, fit major terminus circumferentiae
|
|