Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 361]
| |||||
Appendice
| |||||
[pagina 362]
| |||||
p. 288-290 qui précèdent - Huygens s'exprime comme suit au sujet de l'équation du quatrième degré dont le deuxième terme fait défaut, et de la conséquence qui en découle (il prend ici une hyperbole au lieu d'une ellipse): Soit la parabole CE [Fig. 51], dont l'axe est CB et l'hyperbole FE dont l'axe FB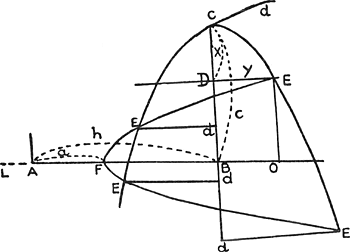 [Fig. 51]
sasse des angles droits avec CB. Et des 4 points E de leur intersection soient menees sur CB les perpendiculaires ED. Je dis que celles qui sont d'un costè seront ensemble egales a celles qui sont de l'autre costè. Soit FL le diametre transverse de l'hyperbole, et son demi diametre transverse AF soit ∞ a, son demi costè droit ∞ b. la distance AB ∞ h, BC ∞ c, le costè droit de la parabole ∞ d. CD ∞ x, DE ∞ y.  Mais OE estant egale a DB elle est c - x. Donc son quarrè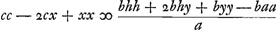 mais, à cause de la parabole, DC est egale à yy/d c'est a dire au quarrè DE appliquè au costè droit d. Donc en substituant dans l'equation trouvée cette valeur au lieu de x, l'on aura mais, à cause de la parabole, DC est egale à yy/d c'est a dire au quarrè DE appliquè au costè droit d. Donc en substituant dans l'equation trouvée cette valeur au lieu de x, l'on aura 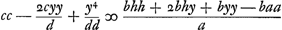
| |||||
[pagina 363]
| |||||
qui est une aequation quarrequarrée qui estant reduite manque de second terme, puisqu'il n'y aura point de y3Ga naar voetnoot3). Et de quelque maniere que la parabole soit couppée par une section conique dont l'axe soit parallele ou a angles droits a celuy de la parabole il est aisè de voir qu'il n'y pourra avoir dans la premiere equation que yy, y et xx et x. Et x estant tousjours ∞ yy/d, il ne peut ij venir en substituant cette quantitè au lieu de x, que yy et y4, et non y3. Or ce second terme manquant a l'equation il est certain que les valeurs de la racine y affirmatives seront ensemble egales aux valeurs negatives de la mesme y. C'est a dire les perpendiculaires DE d'un costè de l'axe CB egales aux perpendiculaires DE de l'autre costè. Car si ces perpendiculaires de l'un costè sont appellées l et m, de l'autre - n et -p ... ou plutôt, pour reproduire exactement le texte, ÷ n et ÷ p. En d'autres endroits aussi on rencontre parfois chez Huygens, au lieu du signe -, le signe ÷ qui a peut-être été inventé par Albert Girard. On ne trouve toutefois ce signe, au lieu du signe -, qu'une seule fois dans l'‘Invention nouvelle en l'algèbre’ de Girard de 1629 (citée à plusieurs reprises par van Schooten dans ses ‘Commentarii’ et ailleurs et sur laquelle on peut consulter aussi la note 120 de la p. 217 qui précède). C'est dans cette brochure que se trouvent les théorèmes sur les relations entre les coëfficients et les racines d'une équation algébrique à une inconnue; mais nous n'osons pas conclure de l'emploi du signe ÷ que Huygens l'avait sous les yeux en ce moment. donc puisque y ∞ l et y ∞ m, et y ∞ -nGa naar voetnoot4) et y ∞ -pGa naar voetnoot4) il s'ensuit que
Et le produit de ces quatre quantitez fera une aequation quarrè quarrée. dont chaque terme sera necessairement egal a chaque terme de l'equation quarrè quarrée qui a este trouvée auparavant. Mais dans cette premiere le terme sous y3 estoit ∞ 0. donc dans l'autre equation le terme sous y3 qui est + ny3 + py3 - my3 - ly3 doit aussi estre ∞ 0, et par consequent n + p egal à m + l. Et la mesme chose devroit estre si trois de ces racines estoient avec le signe contraire de la quatrieme, c'est a dire si trois perpendiculaires tomboient d'un costè et une seule de l'autreGa naar voetnoot5). Dans le Manuscrit E il n'est pas encore question de la deuxième Proposition (ou deuxième lemme) de la Pièce XIII, et Apollonios n'y est pas cité. | |||||
[pagina 364]
| |||||
B. Ailleurs (Chartae mathematicae, f. 163) Huygens donne - évidemment un peu plus tard - une démonstration du même théorème sans faire usage de géométrie analytique. Elle a déjà été publiée en 1921 par F. Schuh, avec notre ‘Pièce XIII’, sous le titre ‘Deux démonstrations dues à Huygens de son théorème concernant les quatre points d'intersection de deux coniques à axes parallèles’ dans le T. I de la revue ‘Christiaan Huygens’ (réd. F. Schuh, Noordhoff, Groningen). Schuh y parle, comme nous l'avons aussi fait plus haut, de l'influence de de la Hire. Voici cette démonstration géométrique des Chartae mathematicae: 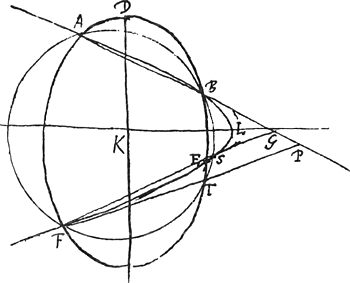 [Fig. 52]
Si deux sections coniques ADB,ALF [Fig. 52], s'entrecouppent en 4 points, A, B, E, F, et que leur axes DK, LK soient paralleles, ou à angles droits, les 4 points d'intersection seront dans un cercle. Car ayant descrit par les 3 points F, A, B un cercle, si ce cercle ne passe pas par le 4e point E; il couppera donc les 2 sections en deux points differents. En marge: Mais on prouvera que cela est impossible. Donc il les couppera au point E qui est leur intersection. En marge: Posons que le cercle couppe la section ALF au point S, et la section ADB au point T. Ayant menè les droites AB, FS, posons qu'elles se rencontrent en quelque point G. Et que FT rencontre la mesme AB en P. Puisque donc, à cause du cercle les rectangles AGB, FGS sont egaux, il s'en suit par la 17.3. des ConicaGa naar voetnoot6) que les droites AG, FG sont egalement inclinees sur l'axe LK de la section ALF. Et par la mesme proposition puisque les rectangles APB, FPT | |||||
[pagina 365]
| |||||
sont egaux à cause du cercle, les droites AP, FP seront egalement inclinees sur la mesme LK, parce qu'elle est perpendiculaire ou parallele a l'axe DK de la section ADB. Donc puisque AG, AP est la mesme ligne droite, il s'ensuit que FG, FP font aussi une mesme droite; parce qu'autrement elles seroient differemment inclinees sur LK. Les points S, T, sont donc dans une mesme droite menée du point F. Et il s'ensuit que ces mesmes points S, T sont coincidents en un, puisqu'ils sont dans une mesme circonference descrite par le point F. Car autrement il faudroit que la droite menee du point F rencontrast la circonference en deux autres points que F. Que si l'on dit que les droites AB, FS peuvent estre paralleles, je dis que si elles sont paralleles, la droite qui joint leur points du milieu sera le diametre du cercle, et sera perpendiculaire a ces deux droites AB, FS. Mais la mesme ligne de jonction sera aussi l'axe de la section ALF parce qu'elle est son diametre a cause du parallelisme des AB, FS, et qu'elle est a angles droits aux appliquees. Donc les lignes AB, FS seront perpendiculaires a l'axe de la section ALF. Et cela estant je dis que la ligne FT sera aussi parallele à AB, car posons qu'elles concourrent; elles seront donc egalement inclinees sur l'axe de la section ADTF par la proposition de ApolloniosGa naar voetnoot6). Mais AB estoit perpendiculaire à l'axe de la section ALF, donc aussi FT, ce qui est absurde puisqu'on les a dit concourrir ensemble. Donc si AB est parallele a FS elle est aussi parallele a FT, et ainsi FS, FT une mesme ligne. l'on montrera de mesme que si FT est parallele a AB, aussi FS sera parallele a AB. Donc si FS concourt avec AB, aussi FT concourra avec AB. Mais toutes les 2, FS, FT seront egalement inclinees a l'axe de la section ALF, avec AB, donc toutes deux concourrent avec AB vers le mesme costè. |
|

