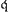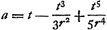Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 367]
| |
Les trois grands problèmes de l'antiquité. | |
[pagina 369]
| |
Avertissement.Dans l'Avertissement précédentGa naar voetnoot1) nous n'avons voué que quelques mots au problème ancien de la quadrature du cercle dont l'impossibilité n'a pas été rigoureusement démontrée au dix-septième siècleGa naar voetnoot2). Quant aux deux autres grands problèmes, celui de la trisection de l'angle dont Huygens s'était beaucoup occupé jadisGa naar voetnoot3) et celui de la recherche de la duplication du cube, autrement dit de deux moyennes proportionnelles entre deux grandeurs données (problème déliaque), ils conduisaient tous les deux à des équations du troisième degré; il a été question du problème déliaque et de la résolution graphique des équations qui s'y rattache, outre dans quelques Tomes précédents, dans plusieurs pages du présent TomeGa naar voetnoot4). Comme on peut le voir au Manuscrit D, la dispute avec Gregory amena Huygens à poursuivre la recherche de solutions approchées pour la quadrature du cercle. Nous publions ici séparément (Pièce II) quelques pages de ce Manuscrit qui auraient pu figurer parmi les AppendicesGa naar voetnoot5) à la Pièce VI dans lesquels on trouve également certaines approximations nouvelles. Ces pages se rattachent au traité ‘De Circuli Magnitudine inventa’ de 1654. | |
[pagina 370]
| |
Il est bien connu que déjà dans l'antiquité la recherche de la quadrature du cercle conduisit Archimède à celles de la quadrature de la parabole et de la spirale qui porte son nom. Dans le ‘De Circuli Magnitudine inventa’ Huygens a constamment présentes à son esprit des propositions exprimant des égalités pour la parabole et donnant lieu par analogie à des théorèmes exprimant des inégalités pour le cercle ou sa circonférence. D'une façon générale on peut dire que dans l'esprit de Huygens comme dans celui de plusieurs de ses contemporains les quadratures d'autres surfaces planes et aussi les rectifications de certaines lignes courbes planesGa naar voetnoot6), constituaient des préparations, des ἀπαγωγάς - voyez p.e. ce mot (si souvent employé par Slusius) dans un passage de Wallis cité plus hautGa naar voetnoot7) - pour la quadrature espérée du cercle. Huygens, on l'a vu plus hautGa naar voetnoot8), admet les nombres entiers, les nombres fractionnaires et les nombres sourds ou irrationnels quoiqu'en vérité ces derniers ne soient pas exprimables par des nombres déterminés de chiffres mais seulement par des lignes (on considère évidemment généralement des lignes droites). Dans l'esprit de Huygens la question de la possibilité de la rectification de la circonférence de cercle revient donc à celles-ci: 1. une ligne peut-elle avoir une longueur telle, par rapport à l'unité donnée de longueur, qu'elle ne soit exprimable ni par un nombre entier, ni par un nombre fractionnaire, ni par un nombre sourd? 2. dans l'affirmative, en est-il ainsi, ou n'en est-il pas ainsi, de la circonférence de cercle par rapport à son rayon? La première question peut être formulée plus brièvement (quoique moins clairement) comme suit: existe-t-il un nombre correspondant à une longueur quelconque? Question à laquelle nous pourrions tout-de-suite (en nous considérant comme des gens du dix-septième siècle) donner une réponse négative, si nous n'avions pas adopté avec Huygens et tant d'autres la convention peut-être assez illogique de parler de ‘nombres sourds’. Depuis des temps fort reculés sans doute les penseurs ont fait une distinction entre la quantité discrète et la quantité continue (voyez p.e. sur ce sujet la note 3 de la p. | |
[pagina 371]
| |
11 qui précède). Depuis l'introduction par MénaechmeGa naar voetnoot9) de courbes donnant par intersection deux longueurs (deux coördonnées, peut-on dire) représentant les deux moyennes proportionnelles entre deux quantités pouvant être, semble-t-il, non seulement des longueurs, mais aussi des nombres, il pouvait sembler désirable d'attribuer une valeur numérique à une longueur quelconque, malgré l'impossibilité de dire exactement ce qu'il faut entendre par une telle valeur numérique. Nous avons dit plus hautGa naar voetnoot10) qu'Aristote ne craint pas d'appliquer le mot ἀριϑμός à une quantité qui varie d'une manière continue. Il est vrai que cet ἀριϑμὸς τῆς ϰινήσεως, le temps qui s'est ‘écoulé’ depuis un instant déterminé, n'est pas une longueur spatiale. Toutefois, après ce premier pas, d'autres - nous songeons surtout à Barrow (note 19 qui suit) - pouvaient avoir l'audace de parler aussi de nombres correspondant à des longueurs spatiales quelconques. D'ailleurs, vers le commencement du dix-septième siècle, plus précisément en 1585, Simon Stevin dans ‘le Premier Livre d'Arithmetique’ avait déjà dit clairement, sans citer Aristote, que, ‘nombre n'est poinct quanite discontinue ... à une continue grandeur correspond le continue nombre qu'on lui attribue ... le nombre est quelque chose telle en grandeur, comme l'humidité en l'eau ...’Ga naar voetnoot11). Ceci mériterait, ajoute l'édition de 1634 de Girard, ‘un traicte particulier’, mais ‘ce ne sera pas icy son lieu’Ga naar voetnoot12). Nous ne trouvons pas que Stevin ait jamais tâché de justifier | |
[pagina 372]
| |
ses affirmations: dans sa thèse c'est le bon sens, l'intuition, qui a la parole et non pas la logique. Le noeud gordien n'est pas défait, il est tranché par un coup d'épéeGa naar voetnoot13). Huygens n'a jamais avancé pareil axiome. Il est vrai que chez lui, comme chez tant d'autres, lorsqu'il se sert de l'expression ‘quantitas’Ga naar voetnoot14), on peut parfois être en doute s'il entend parler exclusivement d'une longueur ou bien peut-être aussi d'une quantité numériqueGa naar voetnoot15); ce qui certes ne suffit nullement pour le considérer comme un partisan de la thèse de StevinGa naar voetnoot16). Nous avons déjà ditGa naar voetnoot17) qu'il déclare expressément ne pas être satisfait de certains raisonnements, ou de certaines définitions, lui paraissant médiocrement logiques, de Wallis. Nous croyons donc aussi pouvoir admettre qu'il est en désaccord avec ce mathématicien là où celui-ci, traitant dans son ‘Arithmetica universalis’ de 1655Ga naar voetnoot18) de la ‘quantitas continua’ ou ‘magnitudo’ d'une part, de la ‘quantitas discreta’ ou ‘numerus’ de l'autre, pense bien faire en effaçant plus ou moins cette distinctionGa naar voetnoot19). Notons que dans l'‘Arithmetica infinitorum’, datant également de 1655Ga naar voetnoot18), Wallis ditGa naar voetnoot20) être convaincu ‘rationem illam | |
[pagina 373]
| |
quae quaerebatur [le rapport de la longueur de la circonférence du cercle à son diamètre] ejusmodi esse ut quae nec veris numeris, nec quidem radicibus surdis (vulgo dictis) esset explicabilis ... alium aliquem notationis modum quam qui adhuc receptus est introducendum putavi, quo numerus ille impossibilis [nous soulignons] indicetur’. Wallis fait allusion à son célèbre théorème exprimant le ‘numerus impossibilis’ par la fraction 3 · 3 · 5 · 5 · 7 · 7 .../2 · 4 · 4 · 6 · 6 · 8 ...Ga naar voetnoot21) (à laquelle se rapporte aussi la courbe suspecte aux yeux de HuygensGa naar voetnoot22) dont il fut question à la p. 234 qui précède) fraction dont Huygens dit admirer la découverte ‘utique si vera est’, ce qui lui semble probableGa naar voetnoot23). On conçoit que Wallis, par cette découverte, croyait avoir démontréGa naar voetnoot24) ce qui à | |
[pagina 374]
| |
son avis comme à celui de Huygens n'était pas démontré dans un ouvrage postérieur par Gregory, que le ‘numerus impossibilis’ n'est pas un nombre dans le sens que Huygens attribuait à ce motGa naar voetnoot25). Huygens, lui, n'a jamais accordé - voyez la Pièce IV qui suit - qu'il fût prouvé que ce ‘numerus’ dit ‘impossibilis’ ne peut pas être un nombre dans le sens restreint dont il vient d'être questionGa naar voetnoot26). Ne réussissant pas à trouver ce nombre il a dû se contenter d'obtenir par des artifices géométriques des valeurs approchées qui peu à peu perdaient leur intérêt. La Pièce II qui suit représente un effort de ce genre dont le résultat n'a pas été publié par luiGa naar voetnoot27). Lorsqu'il avait été démontré par Leibniz que le ‘numerus impossibilis’ - nous parlons toujours de notre nombre π (notation du dix-huitième siècle) - peut être exprimé par la somme algébrique d'une infinité de fractions numériques, Huygens put espérer (Pièce III) que le problème de la quadrature du cercle se montrerait résoluble par la sommation effective des termes de cette série. Le traité d'algèbre de 1685 de Wallis fit connaître à Huygens les approximations de Newton déduites de développements en séries que Newton compare avec celles de Huygens (‘De Circuli Magnitudine inventa’ de 1654). Wallis cite deux lettres de 1676 de Newton à Oldenburg, dont ce dernier envoya des copies tant à Leibniz, auquel elles étaient destinées en premier lieu, qu'à lui. Wallis les avait reçues en juillet 1677 peu avant la mort d'Oldenburg (septembre 1677). On voit par la Pièce IV qui suit que Huygens n'en reçut pas de copies et qu'il apprit seulement à les connaître (ou plutôt à connaitre les grands extraits de ces lettres qui se trouvent dans le livre de Wallis) en 1685 ou 1686. Il s'agit des lettres de Newton à Oldenburg du 13 juin et du 24 octobre 1676, quoique - soit dit en passant - Wallis en deux endroits donne à cette dernière lettre la date du 24 août 1676Ga naar voetnoot28). C'est aux formules de Wallis et de Brouncker que se rattache (même Pièce) le développement par Huygens du ‘nombre π’ en une fraction continue. | |
[pagina 375]
| |
En 1691, ou plutôt déjà en 1689, Huygens revint dans le Manuscrit G (notre Pièce V) sur la ‘Progressio Leibnitsij ad Circuli Quadraturam’ (Pièce III), l'étendant ‘ad sectores quosvis, quod ille nescio an animadverterit’Ga naar voetnoot29). En d'autres termes il démontra, géométriquement, la série arc tg 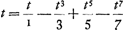 etc.Ga naar voetnoot30) pour des arcs quelconques inférieurs à 45o (ou = 45o). etc.Ga naar voetnoot30) pour des arcs quelconques inférieurs à 45o (ou = 45o).
Les considérations géométriques sont de 1689; elles se rattachent à des considérations géométriques de 1674. La série qui en résulte est de 1691. Tandis que celle de Leibnitz (trouvée d'abord d'une autre façon) est le développement de arc tg i (notation moderne), Huygens propose de prendre plutôt arc tg ⅓√3 ce qu'il appelle la ‘progressio optima ad quadrandum circulum’. Le développement en série de l'arc tangente était connu depuis plusieurs années à diverses personnes: James GregoryGa naar voetnoot31) en avait fait part à John Collins en 1670, mais sans en donner aucune démonstration. En novembre 1690Ga naar voetnoot32) Leibniz écrit à Huygens que dans l'ouvrage qu'il avait ‘composé autrefois sur la quadrature Arithmétique’Ga naar voetnoot33) il avait démontré une proposition générale pour les secteurs des coniques qui, pour le cercle, revient à la formule arc tg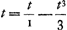 etc. Huygens n'a peut-être pas eu cette formule sous les yeux avant ce tempsGa naar voetnoot34). Le bout de phrase cité plus etc. Huygens n'a peut-être pas eu cette formule sous les yeux avant ce tempsGa naar voetnoot34). Le bout de phrase cité plus
| |
[pagina 376]
| |
haut ‘ad sectores quosvis [secteurs de cercle], quod nescio an ille [Leibniz] animadverterit’ est écrit en marge à la suite d'une considération géométrique de 1689 d'où Huygens peut déduire la formule générale de l'arc tangente. Nous ignorons si cette remarque écrite en marge date de 1689 ou de 1691. Il en est de même d'une autre remarque sur le même sujet, également écrite en marge (fin du § 3 de la Pièce V), où Huygens renvoie à la page ultérieure, datant de 1691, du Manuscrit G où se trouve la série arc tg t = etc. Il est évident que ce renvoi ne peut en tout cas pas être antérieur à 1691. Nous inclinons à croire que les deux remarques marginales datent de cette année. Dans ce cas le ‘nescio an animadverterit’ ne se rapporte pas à un doute sur la connaissance de Leibniz de la formule générale (nous parlons toujours du cercle), mais au fait que Leibniz peut ne pas avoir su qu'elle peut être démontrée de la façon que Huygens indique. La démonstration de Huygens revient à ceci. Il savait depuis 1674 qu'une certaine aire comprise entre trois droites et la courbe à équation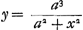 (la ‘versiera’, comme on dira plus tard) est égale à un cercle de rayon ½a et peut d'autre part s'exprimer par a2 (1/1 - ⅓ + ⅖ etc.), d'où résulte la formule de Leibniz. En 1689 il découvre qu'en calculant une aire moins étendue également limitée par trois droites et par la versiera on obtient la surface d'un secteur du même cercle. Or, cette aire peut aussi être exprimée par une série analogue à la précédente. D'où résulte la formule générale qu'il aurait pu déduire en 1689 mais qu'il n'a peut-être déduite en effet qu'en 1691.
Huygens dit que sa ‘progressio optima’ est ‘simplicior ac commodior’ que la ‘progressio Newtoniana’. Il s'agit sans doute de la formule de Newton de la p. 392 qui suit: arc (la ‘versiera’, comme on dira plus tard) est égale à un cercle de rayon ½a et peut d'autre part s'exprimer par a2 (1/1 - ⅓ + ⅖ etc.), d'où résulte la formule de Leibniz. En 1689 il découvre qu'en calculant une aire moins étendue également limitée par trois droites et par la versiera on obtient la surface d'un secteur du même cercle. Or, cette aire peut aussi être exprimée par une série analogue à la précédente. D'où résulte la formule générale qu'il aurait pu déduire en 1689 mais qu'il n'a peut-être déduite en effet qu'en 1691.
Huygens dit que sa ‘progressio optima’ est ‘simplicior ac commodior’ que la ‘progressio Newtoniana’. Il s'agit sans doute de la formule de Newton de la p. 392 qui suit: arc 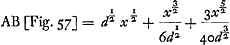 etc., où d est le diamètre du cercle considéré et x la flèche AD de la Fig. 57Ga naar voetnoot35); formule dont Huygens peut avoir causé avec Fatio de Duillier lorsque celui-ci le visita en février 1691 - voyez la p. 396 qui suit - puisque Fatio lui écrit en décembre 1691Ga naar voetnoot35), en citant l'‘Algebra de Mr. Wallis’, en avoir trouvé la démonstrationGa naar voetnoot36). etc., où d est le diamètre du cercle considéré et x la flèche AD de la Fig. 57Ga naar voetnoot35); formule dont Huygens peut avoir causé avec Fatio de Duillier lorsque celui-ci le visita en février 1691 - voyez la p. 396 qui suit - puisque Fatio lui écrit en décembre 1691Ga naar voetnoot35), en citant l'‘Algebra de Mr. Wallis’, en avoir trouvé la démonstrationGa naar voetnoot36).
| |
[pagina 377]
| |
Nous n'avons pas de Pièce de 1666 ou postérieure à cette année qui traite spécialement de la trisection de l'angle. Au sujet du problème déliaque (Pièce VII) on pourrait se demander, en ayant égard à la première partie du présent Tome, si Huygens ne l'a pas parfois considéré dans un rapport étroit avec l'interpolation de tons dans l'échelle musicale. Il faut répondre à cette question qu'il s'est borné à chercher des solutions géométriques, naturellement en faisant usage d'algèbre. Dans l'antiquité aussi, malgré le rapport étroit existant selon plusieurs entre la mathématique et la musique - on peut consulter l'ouvrage de Théon de Smyrne, cité plus hautGa naar voetnoot37) - ce problème, si nous nous en tenons aux textes, paraît avoir été considéré comme essentiellement de nature géométrique. Huygens n'a recours aux logarithmes que lorsque le nombre de termes à interpoler, soit en musique, soit dans d'autres cas pratiques (voyez la p. 294 qui précède), devient plus grand. |
|