Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 334]
| |
Appendice
| |
[pagina 335]
| |
proderet. Jam vero post annos aliquot in Apolloniano problemateGa naar voetnoot3) eandem rationem expertus, ubia puncto dato in datam conisectionem perpendicularis duci imperatur, quod ille ut solidum construit eoque ab alijs reprehendi meruit, inveni solutionem problematis ejus circuli ope ac solîus quae data est sectionis conicae, quod in parabola quidem jam olim praestiteramGa naar voetnoot4), sed in hyperbola et ellipsi multo plus erat negotij, cum autem longiuscula in his esset constructio mea eoque dubitarem an non melior quaepiam invenienda restaret, operae pretium non duxi adversarijs eam describere. Postquam vero gallus quidam geometraGa naar voetnoot5) Slusiana methodo usus, multo operosiorem longioremque solutionem ejusdem problematis edidisset, tunc demum alicujus pretij mea esse mihi visa est, simulque intellexi methodum qua eam inveneram anteponendam Slusianae methodo ad solida pleraque problemata, cum et compendiosior sit nec tantis quaerendi ambagibus obnoxiaGa naar voetnoot6). Inventa solutione per circulum et coni sectionem similem datae, habetur simul solutio per circulum et ipsam sectionem datam, quod d. Slusius in Mesolabo videtur animadvertisse. Inventis enim Ellipsis similis quae describenda non est latere transverso, item circuli, qui illam intersecando problema solvit, diametro; et positione centri ad Ellipsis illius latus transversum. opus tantum est omnia haec augere vel minuere proportionaliter, secundum rationem dicti lateris transversi ad latus transversum ellipsis datae, peractaque constructione qualis inveniebatur cum Ellipsi simili facienda, prodibit non quidem linea quaesita sed ejusmodi quae reducta proportione priori contrariâ, quaesitam exhibeat. | |
[pagina 336]
| |
B.C. Constructio problematum solidorum per resolutionem aequationis in duos locos.BGa naar voetnoot1). § 1. Sit data aequatio abb ∞ x3, quae est ad inveniendas duas medias proportionales inter datas lineas a et b. Est enim hic x mediarum altera, proxima datae b Primum utramque aequationis partem duco in x, fit x4 ∞ abbx, tum divido per bb, sit x4/bb ∞ ax. Jam utrimque addo - xx + ¼bb, fit x4/bb - xx + ¼bb ∞ ax - xx + ¼bb. ut nempe ea pars ubi est x4/bb fiat quadratum; ex altera parte vero accedat - xx, quod cur fiat jam parebit. Aequetur enim utraque pars aequationis quadrato yy, positâ y linea incognita cui x sit ad rectos angulos. fit igitur 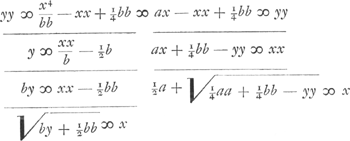 Altera harum aequationum significat locum ad parabolam. Cujus parabolae latus 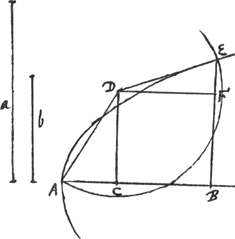 [Fig. 42]
rectum est b. Altera significat locum ad circuli circumferentiam, cujus radius 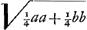 . Haec oritur igitur constructio problematis, per parabolam et circuli circumferentiam, quae est hujusmodi. . Haec oritur igitur constructio problematis, per parabolam et circuli circumferentiam, quae est hujusmodi.
Sint datae extremae a, b. In recta AB [Fig. 42] accipiatur AC ∞ ½b, cui ponatur ad angulos rectos CD ∞ ½a, junctâque AD, sit haec radius circumferentiae describendae centro D. Intelligatur etiam descripta parabola cujus axis AB, vertex A, latus rectum aequale b. Haec circumferentiam secet in E puncto, unde cadat in axem AB per- | |
[pagina 337]
| |
pendicularis EB. Erit mediarum quaesitarum altera EB, proxima nimirum datae b; altera BA. Si enim CB vocetur y; BE, x; erit AB ∞ ½b + y cum AC sit ½b. Rectangulum vero ex AB et latere recto b, erit ½bb + by, aequale propter parabolam quadrato ex EB, nempe xx. Rursus cum quadratum ex AD sive ex DE sit ¼aa + ¼bb, quadratum vero DF, perpendicularis in EB, sit yy, erit EF quadratum ∞ ¼aa + ¼bb - yy. unde EF + FB, sive EB hoc est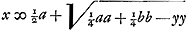 . Hinc autem, relegendo aequationis superioris vestigia, apparet fieri ax - xx + ¼bb ∞ yy. Item ex ½bb + by ∞ xx, quod supra, relegendo similiter vestigia alterius aequationis, apparet fieri . Hinc autem, relegendo aequationis superioris vestigia, apparet fieri ax - xx + ¼bb ∞ yy. Item ex ½bb + by ∞ xx, quod supra, relegendo similiter vestigia alterius aequationis, apparet fieri
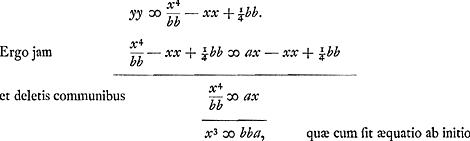 quae cum sit aequatio ab initio proposita, constat eam recte constructam fuisse, et esse continuè proportionales b, x, xx/b, a. Patet etiam BA esse alterum proportionalem xx/b, cum, ex proprietate parabolae, sit latus rectum b, ad applicatam BE, sive x, ut haec ad BA sive xx/b. Est autem constructio haec eadem, quae CartesijGa naar voetnoot2).
B. § 2. Data eâdem aequatione x3 ∞ abb, atque inde, ut ante, x4/bb ∞ ax, si utrimque addatur + xx + ¼bb, et pars utraque aequationis aequetur vv quadrato incognitae v, quam pono perpendicularem in x, fiet hinc quidem vv ∞ x4/bb + xx + ¼bb, hoc est, extracta radice, v ∞ xx/b + ½b, sive bv ∞ xx + ½bb quod significat locum ad para- | |
[pagina 338]
| |
bolam, cujus latus rectum b. Ex altera vero parte fiet vv ∞ ax + xx + ¼bb, qui est locus ad hyperbolen aequalium laterum, cum habeatur + xx, nullâ proportione affectum, desit autem xv. cujus hyperbolae latus transversum est 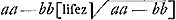 . Hinc igitur datur constructio problematis per intersectionem parabolae et hyperbolae aequilaterae. . Hinc igitur datur constructio problematis per intersectionem parabolae et hyperbolae aequilaterae.
Sed hujusmodi constructio merito rejicitur, cum constet una coni sectione et circuli circumferentia rem conficiGa naar voetnoot3). Nec tamen frustra est illa resolutio in parabolam et hyperbolen aequalium laterum, ut jam ostendemus; id quo in hac methodo praecipuum est ac pulcherrimum. Ex eo enim quod paulo ante invenimus problema construi intersectione parabolae cujus latus rectum b, et circuli circumferentiae: nunc vero idem rursus construi ostendimus intersectione ejusdem parabolae, cujus latus rectum b, et hyperbolae aequilaterae. Hinc inquam colligere licet, intersectionem utramque in idem parabolae punctum casuram, ac proinde in idem hoc punctum etiam cadere intersectionem hyperbolae aequilaterae et circumferentiae circuli. Ita ut jam harum tantum duarum intersectione ad constructionem opus habeamus, omissa parabola. Scimus enim, in superiori constructione, posita CB in axe parabolae ∞ y, et BE ∞ x quae sit ipsi CB ad angulos rectos, esse quidem hanc ordinatim ad axem applicatam. Rursus vero in posteriori constructione scimus, positâ v in ejusdem parabolae axe, esse itidem lineam quaesitam x in eadem parabola ordinatim applicatam, ac proinde eandem ipsi BE ante inventae. Itaque si parabola intelligatur AE latus rectum habens b, cumque eâ sigillatim utraque constructio perficiatur, tam quae intersectione circumferentiae circuli opus habebat, quam quae hyperbolen aequalium laterum requirit, necesse est hoc modo intersectionem circumferentiae et hyperbolae aequilaterae ostendere punctum E, unde ducto in AB perpendiculari EB, sit quaesitae x aequalis. idque ita ut parabolam describere opus non sit. Construetur igitur problema intersectione hyperbolae aequilaterae et circumferentiae circuli hoc modo [Fig. 43]. Circulus quidem eodem modo ac superius describatur AE. Porro producta BA ad G, ut sit AG aequalis AC, hoc est ½b, factaque GH perpendiculari aequali ½a, et quadrato HK aequali differentiae quadratorum HG, GA, centro H, axe HG, vertice K sit descripta hyperbole aequalium laterum KAE, quae secet circumferentiam AE in E, et sit EB perpendicularis in EB, haec ipsa EB erit linea x quaefita. | |
[pagina 339]
| |
Si enim CB [Fig. 43] ut ante vocetur y, BE, x. fit propter circulum, ut supra,
 [Fig. 43].
yy ∞ ax - xx + ¼bb. Rursus si GB seu KH vocetur v, erit summa quadratorum KH, HK, vv + ¼aa - ¼bb. cui summae aequale est, propter hyperbolen aequilateram, quadratum ex KE. unde 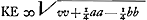 , et BE sive , et BE sive 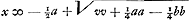 . Hoc est, vv ∞ ax + xx + ¼bb: sive (quia v, hoc est GB, est y + b) . Hoc est, vv ∞ ax + xx + ¼bb: sive (quia v, hoc est GB, est y + b)
yy + 2by + bb ∞ ax + xx + ¼bb, hoc est yy ∞ ax + xx - 2by - ¾bb. Erat autem prius  B § 3. Facilius alia hyperbole circa asymptotos invenietur quae cum eodem rursus circulo problema construat. posita enim aequatione x3 ∞ abb, fiet xx ∞ abb/x. jam si utraque pars aequetur vb, positâ v incognitâ, fiet ex altera parte xx ∞ vb. quae est aequatio ad parabolam, cujus, ut in superioribus, latus rectum est b. Ex altera vero abb/x ∞ bv, hoc est ab ∞ xv, quae est aequatio ad hyperbolam ad asymptotos, et quidem aequalium laterum si v et x angulo recto jungi intelligantur, quod semper in his fieri volumus. Posita autem parabola AE, cujus ut antea latus rectum b, facile apparet quomodo collocanda sit hyperbola de qua hic agitur. Quia enim aequatio parabolae est | |
[pagina 340]
| |
xx ∞ vb, oportet AB vocari v, ut rectangulum vb aequetur quadrato BE, quod est xx. Quia porro aequatio hyperbolae est ab ∞ xv, hoc est ab ∞ rectang. AB, BE, apparet asymptotos esse AB, AM angulum rectum ad A constituentes, factoque rectangulo AL ex lateribus a, b, hyperbolam per L punctum describendam, quae circumferentiam AE in puncto E saepe dicto sectura sit. Facilisque est demonstratio. Nam cum sit, propter circulum, yy ∞ ax - xx + ¼bb, posita ut supra CB ∞ y, et BE ∞ x. Cumque hic sit ab ∞ xv propter hyperbolam, sed v seu BA sit aequalis y + ½b. Erit ergo ab ∞ xy + ½bx, hoc est y ∞ ab/x - ½b. Unde 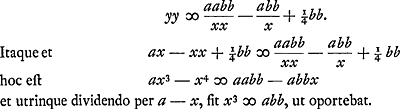 B § 4. Posita rursus aequatione eadem x3 ∞ abb, sive x4 ∞ abbx, sive x4/bb ∞ ax, si utrinque addatur - cxx/b + ¼cc, et utraque pars aequationis aequetur vv fiet 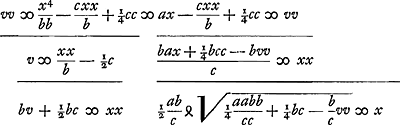 Unde hinc quidem aequatio quae locum ad parabolam designat cujus latus rectum b. Inde vero aequatio quae significat locum ad Ellipsin datae cuivis similem, cujus nempe latus rectum ad transversum ut c ad b, nam c pro arbitrio sumi potest. Dimidium vero lateris transversi ellipseos est 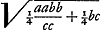 et linea x parallela lateri transverso. Et quoniam in aequatione ad parabolam, latus rectum parabolae est b, idem nempe quod in aequatione superiori ad circuli circumferentiam, hinc oritur problematis constructio, seu inventio duarum mediarum inter duas datas, per circulum et ellipsin similem datae, estque eadem prorfus quae in propos. 1 Slusij in Mesolabo. Unde et altera, propositione ipsius ultimâ, per circulum et ellipsin quamlibet datam facile obtinetur. cum semper data constructione per circulum et ellipsin vel hyperbolen similem datae, facile absque alio calculo inde deducatur constructio per circulum et ellipsin vel hyperbolen datam, quod videtur Slusius non advertisse. et linea x parallela lateri transverso. Et quoniam in aequatione ad parabolam, latus rectum parabolae est b, idem nempe quod in aequatione superiori ad circuli circumferentiam, hinc oritur problematis constructio, seu inventio duarum mediarum inter duas datas, per circulum et ellipsin similem datae, estque eadem prorfus quae in propos. 1 Slusij in Mesolabo. Unde et altera, propositione ipsius ultimâ, per circulum et ellipsin quamlibet datam facile obtinetur. cum semper data constructione per circulum et ellipsin vel hyperbolen similem datae, facile absque alio calculo inde deducatur constructio per circulum et ellipsin vel hyperbolen datam, quod videtur Slusius non advertisse.
| |
[pagina 341]
| |
Hoc vero in sequenti problemate Apolloniano manifestum fiet ubi ex dato puncto ad datam coni sectionem lineam rectam perpendicularem ducemus, ipsius datae sectionis et circuli intersectione, quum Apollonius hyperbolae descriptione utatur, eoque a geometris reprehendi merueritGa naar voetnoot4). Adnoto vero priusquam eo progrediar, potuisse eadem facilitate constructionem duarum mediarum per circulum et hyperbolen datae similem dari, si utrinque addidissem + cxx/b + ¼cc. Indeque etiam per circulum et hyperbolen datam.
CGa naar voetnoot5). § 1. Data Ellipsi, ducere ex puncto intra vel extra eam dato, lineam rectam quae occurrat ipsi ad angulos rectos. 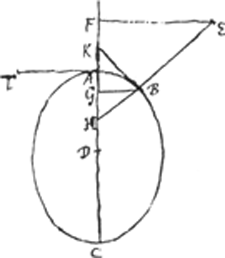 [Fig. 44].
Sit Ellipsis [Fig. 44] cujus axis major idemque latus transversum AC, latus rectum AT, centrum D. deturque punctum E unde oporteat ducere rectam EB quae ellipsi occurrat ad angulos rectos in B puncto. Ponatur factum, occurratque productum EB axi AC in H. Tangens vero in puncto B ideoque recta ad BE, nempe BK, conveniat cum axe in K. Et ducantur ad axem perpendiculares EF, BG. Sit axis AC ∞ a, latus rectum AT ∞ b, DF ∞ c, FE ∞ d, quaesita DG ∞ x. Erit ut a ad b ita rectang. CGA, hoc est ¼aa - xx, ad quadratum GB, quod erit ¼baa - bxx/a. Sicut autem DG, x ad DA, ½a, ita haec ad DK, ¼aa/x, propter tangentem | |
[pagina 342]
| |
BK. Et à DK auferendo DG, x, fiet KG, ¼aa/x - x sive 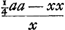 . Ut vero KG ad GB, ita haec ad GH, quae erit bx/a. cui si addatur GF, c - x, fiet HF bx/a + c - x. . Ut vero KG ad GB, ita haec ad GH, quae erit bx/a. cui si addatur GF, c - x, fiet HF bx/a + c - x.
Quod si GB vocetur z, erit ut GH, bx/a ad GB, z ita HF, bx/a + c - x ad FE, d. Ideoque dbx/a ∞ bxz/a + cz - xz, quae aequatio docet locum puncti B esse hyperbolen, atque hinc constructio brevissima quae est apud Apollonium, sed vitiosaGa naar voetnoot6). Quare nos aliam meliorem jam investigabimus in qua non hyperbolâ sed tantum circuli circumferentiâ opus erit.  | |
[pagina 343]
| |
Nempe tantum terminus ppqy habuisset signum + cum prius habuerit signum -, quod etiam cognoscere licet ex Cartesij Regula, quae jubet mutari signa locorum parium (qualis hic sub y, cum y3 non inveniatur) ut radices verae fiant falsae et contra. Falsae enim et hic fiunt radices prius verae y, cum ponimus ½g - x ∞ y. quoniam jam ½g major intelligitur quam x, ideoque y in partem negatam accipienda, hoc est in contrariam ejus quo vergit DG. ponendum autem ½g - x ∞ y quando animadvertimus ½g majorem fore quam x. Quod autem utrobique, si habeatur + ppyy, fiat etiam + ¼ppgr, facile ostenditur. Etenim, si habeatur + ppyy, hoc est si ee majus quam ½gg + ¼aa, fiet etiam 1/16gg + ¼ee majus quam 1/16aa, ideoque + ¼ppgr. at si habeatur - ppyy poterit esse vel + ¼ppgr, vel - ¼ppgr.
C § 2. Ad divisionem porro in duos locos. 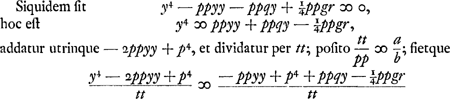 quae pars utraque aequationis ponatur aequalis quadrato vv incognitae quae sit ipsi y perpendicularis; eritque ex altera parte  quae aequatio designat locum ad parabolam cujus latus rectum t. 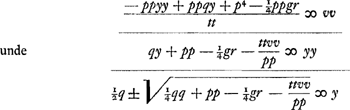 qui est locus ad ellipsin similem datae. nam quia ut pp ad tt ita est axis minor, cui per- | |
[pagina 344]
| |
pendicularis y, ad latus rectum sibi conveniens; erit contra axis major ad latus rectum suum ut tt ad pp, hoc est ut a ad b. Est autem axis major hujus ellipsis 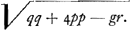 Quod si vero in aequatione fuisset + ppyy, ac proinde y4 ∞ - ppyy + ppqy - ¼ppgr tantummodo utrimque divisissem per tt, ponendo ut ante tt/pp ∞ - a/b; fuissetque
Quod si vero in aequatione fuisset + ppyy, ac proinde y4 ∞ - ppyy + ppqy - ¼ppgr tantummodo utrimque divisissem per tt, ponendo ut ante tt/pp ∞ - a/b; fuissetque 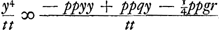 . .
Et aequando rursus utrasque aequationis partes quadrato vv, habuissem hinc vv ∞ y4/tt hoc est v ∞ yy/t vel tv ∞ yy qui locus est ad parabolam cujus latus rectum t. 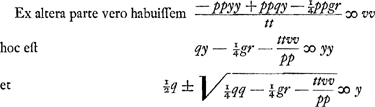 C § 3. Habemus jam constructionem problematis per ellipsin similem datae et per parabolam. Nunc porro alia quaerenda est per parabolen eandem et circulum, qua inventa, habebimus etiam constructionem per ellipsen similem datae et per circulum, atque inde per ellipsin ipsam quae data est, et per circulum.  Subtrahatur utrinque yy sive ttyy/tt. Ergo 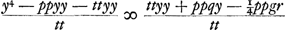 .
Jam, ut ab altera parte fiat quadratum, addendum insuper ¼ quadrati ex .
Jam, ut ab altera parte fiat quadratum, addendum insuper ¼ quadrati ex 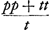 quod vocetur s, itaque addito utrinque ss fiet quod vocetur s, itaque addito utrinque ss fiet 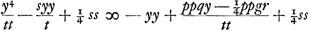 . .
| |
[pagina 345]
| |
Et aequata parte utraque aequationis quadrato incognito z, habebitur 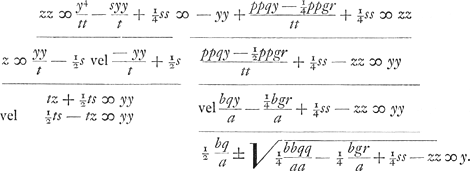 Hinc nimirum aequatio ad parabolam cujus latus rectum t. Inde aequatio ad circuli circumferentiam. Unde datur constructio problematis per hujus parabolae et circumferentiae intersectionem. Et quia etiam antea constructio inventa est per eandem parabolam et ellipsin similem datae, ubi y similiter quoque ad axem applicata erat ut hic, sequitur jam constructionem haberi per ellipsin datae similem et per circuli circumferentiam postremo inventam. Oportet autem, sicut in praecedentibus diximus, ad constructionem hanc; positis parabolae axe et vertice, cujus latus rectum t, quod aequale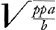 quia posuimus tt/pp ∞ a/b; oportet inquam velut si utramque cum parabola hac constructionem propositam quia posuimus tt/pp ∞ a/b; oportet inquam velut si utramque cum parabola hac constructionem propositam
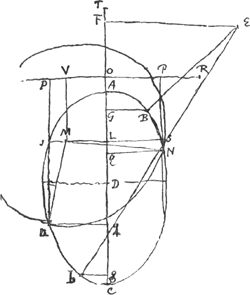 [Fig 45].
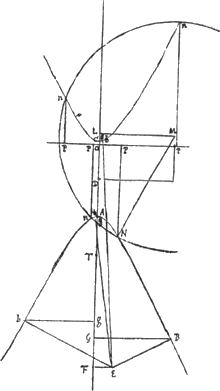
habeamus, tam quae ellipsin quam quae circulum requirit, definire calculo lineas rectas quibusad eas suis locis constituendas opus est, quales aequationes inventae praescribunt. Ita enim cum ad eandem parabolam tam ellipsis quam circuli positus cognoscetur, etiam utriusque horum inter se positus innotescet. Ut autem per ellipsin datam et circulum res absolvatur, opus est tantum ut proportionaliter augeantur vel minuantur lineae quae circuli radium et positionem ipsius ad axem ellipsis similis definiunt, secundum rationem qua ellipsis datae axis superat vel minor est axe ellipsis similis. ac deinde inventa radix reducenda rursus proportione contraria ad obtinendam radicem y. Nempe in constructione per parabolam et ellipsin similem datae, cujus vicem nunc referat ipsa ellipsis ANC [Fig. 45], apparet per- | |
[pagina 346]
| |
pendicularem à centro ellipsis D in axem parabolae (quem referat OP) ductam debere intercipere portionem axis illius ad verticem RO aequalempp/t, propter aequationem ad parabolam yy ∞ tv + pp vel yy ∞ pp - tv. Ipsam vero perpendicularem OD, quae est in axe ellipsis, esse ½q. Rursus in constructione per parabolam eandem et circulum apparet perpendicularem à centre circuli M in axem parabolae intercipere partem VR axis ejus ad verticem, aequalem ½s, propter aequationem ad parabolam yy ∞ ½ts ± tz. Ipsam vero perpendicularem MV esse ½bq/a. Itaque differentia duarum ½q et ½bq/a, hoc est duarum DO, MV, erit pars axis DL, à centro ellipsis, quam intercipit perpendicularis a centro circuli in ipsum axem educta. adeoque DL erit ½ hq/a quia h ∞ a - b. Ipsa vero perpendicularis LM erit differentia duarum ½s et pp/t, hoc est duarum RO, RV. Ideoque LM ∞ ½ht/a quia h ∞ a - b et s ∞ t + pp/t et tt ∞ ppa/b. Radius vero circuli erit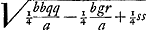 ut patet ex aequatione.
In hac autem ellipsi simili perpendiculares ab intersectionibus N in OP ductae essent radices verae y. Jam vero ut constructio fiat per ellipsin ipsam quae data est, oportet facere sicut axis major ellipsis similis, qui erat ut patet ex aequatione.
In hac autem ellipsi simili perpendiculares ab intersectionibus N in OP ductae essent radices verae y. Jam vero ut constructio fiat per ellipsin ipsam quae data est, oportet facere sicut axis major ellipsis similis, qui erat 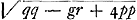 (vocetur autem l) ad a, axem ellipsis datae, ita DL ∞ ½hq/a ad ½hq/l quae erit vera DL qua utendum in ellipsi data. Item ut l ad a ita LM ∞ ½ht/a ad ½ht/l, quae erit vera LM in data ellipsi adhibenda. Ac denique ut l ad a ita radius circuli inventus ad (vocetur autem l) ad a, axem ellipsis datae, ita DL ∞ ½hq/a ad ½hq/l quae erit vera DL qua utendum in ellipsi data. Item ut l ad a ita LM ∞ ½ht/a ad ½ht/l, quae erit vera LM in data ellipsi adhibenda. Ac denique ut l ad a ita radius circuli inventus ad 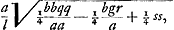 radium circuli quo utendum in ellipsi data.
Itaque in ellipsi data [Fig. 45] accipiatur in axe a centro D recta DL aequalis ½ hq/l. sitque axi perpendicularis LM aequalis ½ ht/l. Erit M centrum circuli, radius vero aequalis radium circuli quo utendum in ellipsi data.
Itaque in ellipsi data [Fig. 45] accipiatur in axe a centro D recta DL aequalis ½ hq/l. sitque axi perpendicularis LM aequalis ½ ht/l. Erit M centrum circuli, radius vero aequalis 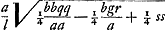 . .
Ab intersectione autem circuli hujus et ellipsis quae sit in puncto N, ducenda perpendicularis NP in rectam OP, axi normalem et abscindentem DO ∞1/2 aq/l à D versus | |
[pagina 347]
| |
L. quia diximus centrum ellipsis similis ab axe parabolae distare ½q; quae reducta, sicut reliquae linea, secundum proportionem l ad a, facit ½aq/l. refert enim sic rursus recta AP axem parabolae. ad quem ducta perpendicularis NP eritay/l. quam reducendo rursus secundum proportionem contrariam a ad l, habebitur y; et ponendo DT ∞ ½g et TG ∞ y, unde DG ℞ ½g - y, erit DG ℞ x quaesitae; quare axi perpendicularis GB quae ellipsi occurrat, ostendet punctum B, ad quod ab E puncto dato ducendo rectam EB, occurrat ipsi ellipsi ad angulos rectos. Potest autem contingere intersectio ellipsis et circuli in punctis quatuor, unde ductis perpendicularibus in OP, ijsque reductis similiter fient singulae y quae ablatae ab ½g, ut accipiuntur à T versus D, dabunt totidem radices x, quae ostendent puncta ellipsis ad quae ipsi ad angulos rectos ducantur à puncto E. C § 4. Et haec quidem rationem methodi perspicue explicant. Si vero breviter solu tionem problematis tradere velimus, ponenda sunt tantum quae pag. 16 et 17 continenturGa naar voetnoot7), vel etiam quae paginis 18, 19, 20, 21Ga naar voetnoot8). Dein ita pergendum. Quodsi y4 - ppyy - ppqy + ¼ppgr ∞ 0, ponatur t ∞ √pp/b, s ∞ pp/t + t,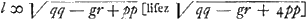 , h ∞ a - b, sicut jam ante positum fuit. Tum a centro ellipsis datae D ponatur in axe ejus, versus F, recta DL ∞ ½hq/l; et erigatur ad axem perpendicularis LM ∞ ½ht/l, statuenda in partem contrariam ejus ubi E punctum. Deinde centro M radio , h ∞ a - b, sicut jam ante positum fuit. Tum a centro ellipsis datae D ponatur in axe ejus, versus F, recta DL ∞ ½hq/l; et erigatur ad axem perpendicularis LM ∞ ½ht/l, statuenda in partem contrariam ejus ubi E punctum. Deinde centro M radio 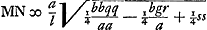 circumferentia describatur, et a punctis N, ubi illa ellipsi occurrit, ducantur NP perpendiculares in OP, quae axem secat ad rectos angulos, abscinditque DO ∞ ½aq/l, idque versus F. Singulae NP vocentur m et ut a ad l ita sit m ad aliam quae vocetur y, et fiat DG ∞ ½g - y, sumpta ½g a D versus F. Denique ducta perpendiculari ad axem rectâ GB, quae occurrat ellipsi in B, jungatur EB: haec occurret ellipsi ad angulos rectos. circumferentia describatur, et a punctis N, ubi illa ellipsi occurrit, ducantur NP perpendiculares in OP, quae axem secat ad rectos angulos, abscinditque DO ∞ ½aq/l, idque versus F. Singulae NP vocentur m et ut a ad l ita sit m ad aliam quae vocetur y, et fiat DG ∞ ½g - y, sumpta ½g a D versus F. Denique ducta perpendiculari ad axem rectâ GB, quae occurrat ellipsi in B, jungatur EB: haec occurret ellipsi ad angulos rectos.
Si ponatur axis ellipsis AC seu a ℞ 1; latus rectum b ∞ ½; DF sive c ∞ 1; FE seu d ∞ √½. fit aequatio y4 - 5/4yy - 5/2y + 7/4 ∞ 0. In cujus constructione signa + et - ita sese habebunt ut in ea quam construere docuimus, quia ipsius aequationis signa | |
[pagina 348]
| |
respondent signis aequationis y4 - ppyy - ppqy + ¼ppgf ∞ 0. Fiunt autem hinc h ∞ ½, g ∞ 2, pp ∞ 5/4, tt ∞ 5/2, q ∞ 2, gr ∞ 28/5, ss ∞ 45/8, l ∞ √17/5, DO ∞ √5/17, DT ∞ 1, DL ∞ ½ √5/17, LM ∞ √1/34. Radius NM ∞ ¾ √½ sive ¾ axis minoris. Sicut autem a ad l, hoc est ficut 1 ad √17/5, ita est NP ad √17/5 NP sive y. Unde DG sive ½g - y erit 1 - √17/5 NP. Quod si ab altera parte centri ponatur Dg ∞ √17/5 np - 1 (est autem np perpendicularis ab altera ellipsis et circuli intersectione, ducta in OP) sitque axi perpendicularis gb. Erit b alterum in ellipsi punctum, ad quod ducta Eb occurrat ipsi ad angulos rectos. Ad demonstrationem, sit NQ perpendicularis ad axem ellipsis. Item sit MS perpendicularis in NP. ut autem a ad l ita sit NQ ad v. Ergo NQ ∞ av/l. Quia autem ut a ad l, ita est NP, sive m ad y, erit m sive NP ∞ ay/l. Jam vero, propter ellipsin, rectangulum CQA, hoc est quadratum DA minus quadrato DQ, est ad quadr. QN, ut axis ellipsis ad latus rectum, hoc est ut a ad b. Sed quadratum DA est ¼aa: quadr. DQ, sive ab DO - NP, est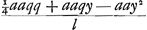 , item quadr. QN, sive nn, est aavv/ll. Hinc igitur, ex proportione ista, datur aequatio ¼bll - ¼bqq + bqy - byy ∞ avv.
Et restituto qq - gr + 4pp in locum ll fit , item quadr. QN, sive nn, est aavv/ll. Hinc igitur, ex proportione ista, datur aequatio ¼bll - ¼bqq + bqy - byy ∞ avv.
Et restituto qq - gr + 4pp in locum ll fit 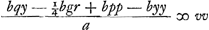 .
Jam porro ut a ad l ita sit MS ad aliam z. Ergo MS ∞ az/l. Est autem, propter circulum, quadr. MN aequale quadratis MS et SN. Sed quadr. radij MN est .
Jam porro ut a ad l ita sit MS ad aliam z. Ergo MS ∞ az/l. Est autem, propter circulum, quadr. MN aequale quadratis MS et SN. Sed quadr. radij MN est 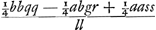 ex constructione, quadratum vero MS est aazz/ll. Et quadr. SN ex constructione, quadratum vero MS est aazz/ll. Et quadr. SN 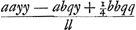 quia SN ∞ NP minus PS sive OL, hoc est ay/l - ½bq/l. quod enim OL ∞ ½bq patet quia DL est ½hq/l hoc est quia SN ∞ NP minus PS sive OL, hoc est ay/l - ½bq/l. quod enim OL ∞ ½bq patet quia DL est ½hq/l hoc est 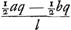 ; DO vero ½aq/l. Fit igitur aequatio ; DO vero ½aq/l. Fit igitur aequatio 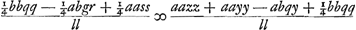 quae reducta facit quae reducta facit 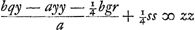 .
Sed quoniam LM erat ∞ ½ht/l, LS vero sive NQ ∞ av/l, erit .
Sed quoniam LM erat ∞ ½ht/l, LS vero sive NQ ∞ av/l, erit 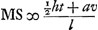 . .
| |
[pagina 349]
| |
Est autem ½ht/l ∞ ½as/l - app/lt ut facile est ostendere, quia h ∞ a - b, et s ∞ t + pp/t, et pp/tt ∞ bt/a. Ergo sit 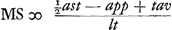 . Sed erat MS ∞ az/l. Ergo haec
aequalia; unde fit z ∞ ½s - pp/t + v. Ideoque zz ∞ ¼ss - spp/t + p4/tt + sv - 2ppv/t + vv. Sed erat inventum . Sed erat MS ∞ az/l. Ergo haec
aequalia; unde fit z ∞ ½s - pp/t + v. Ideoque zz ∞ ¼ss - spp/t + p4/tt + sv - 2ppv/t + vv. Sed erat inventum 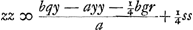 . Unde, substituto in alterutra harum aequationum eo cui aequatur zz in altera, invenitur . Unde, substituto in alterutra harum aequationum eo cui aequatur zz in altera, invenitur 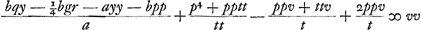 .
ubi si pro -p4/tt substituatur - bpp/a, quia pp/tt ∞ b/a, cum positum fuerit .
ubi si pro -p4/tt substituatur - bpp/a, quia pp/tt ∞ b/a, cum positum fuerit 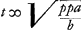 ; atque etiam pro s reponatur ipsi aequale ; atque etiam pro s reponatur ipsi aequale 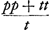 , siet , siet
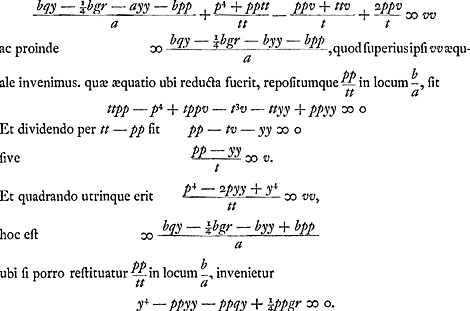 Et hinc quidem facile reliqua demonstratio absolvitur per superioris analyseos regressum. Etenim in hac aequatione repositis pro pp, et ppq, et ¼ppgr, ijs quae per haec superius designavimus, fiet aequatio superior illa y4 - ½ggyy &c. ∞ 0. Et rursus posito y ∞ ½g - x, habebitur aequatio prima x4 - 2gx3 &c. ∞ 0. Unde constat recte se habere constructionem. Et haec quidem una omnia puncta B in ellipsi invenire docet, in demonstratione autem non nulla sed exigua erit diversitas. | |
[pagina 350]
| |
Si in aequatione ∞ 0 habeatur - ¼ppgr, hoc tantum in constructione mutandum, ut termini in quibus gr contraria signa accipiant ijs quae nunc fuere. Sed si in aequatione y4 &c. ∞ 0 fuerit + ppyy; quo casu diximus etiam semper inveniri + ¼ppgr; fiet 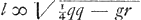 , de caetero autem nihil omnino in constructione priori mutandum. Tunc enim LM quidem statuenda ∞ ½ as/lt; sed s invenitur aequalis t - pp/t. unde LM, sicut ante, fit ½ at/l - ½app/l. , de caetero autem nihil omnino in constructione priori mutandum. Tunc enim LM quidem statuenda ∞ ½ as/lt; sed s invenitur aequalis t - pp/t. unde LM, sicut ante, fit ½ at/l - ½app/l.
C § 5. Problema idem in Hyperbola vel sectionibus oppositis. Sint sectiones oppositae AB, Cb [Fig. 46], axis idemque latus transversum AC, centrum D. Punctum 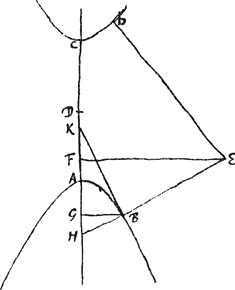 [Fig. 46].
datum E unde oporteat ducere EB quae occurrat hyperbolae ad angulos rectos. Praeparatione eadem adhibita quae fuit in Ellipsi, sint etiam nomina lineis similiter imposita; ut sit AC ∞ a; latus rectum ∞ b; DF ∞ c; FE ∞ d; DG ∞ x. Jam erit rursus ut quadr. GH. ad quadr. GB ita qu. FH ad qu. FE. Invenientur autem qu. GH ∞ bbxx/aa. qu.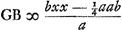 . Qu. FH, posito a + b ∞ h, erit . Qu. FH, posito a + b ∞ h, erit 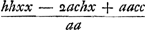 , qu. verò FE est dd. Itaque hinc aequatio orietur, quâ reductâ, et posito x - ½g ∞ y (fiet autem y ∞ ac/h) adauferendum secundum terminum, fiet tandem aequatio , qu. verò FE est dd. Itaque hinc aequatio orietur, quâ reductâ, et posito x - ½g ∞ y (fiet autem y ∞ ac/h) adauferendum secundum terminum, fiet tandem aequatio
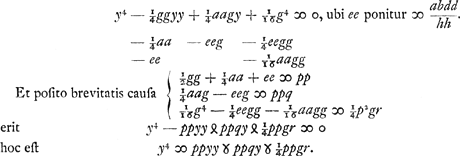 Dividatur per tt indeterminatum; et utraque pars aequetur quadrato incognitae v. Fit | |
[pagina 351]
| |
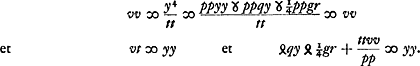 Altera aequatio ad parabolam cujus latus rectum t; altera ad hyperbolam similem datae si ponatur tt/pp ∞ a/b. cujus hyperbolae axis erit 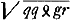 , quod appelletur l. apparet autem fieri , quod appelletur l. apparet autem fieri 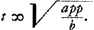 Porro ut aequationes ad circumferentiam circuli, et ad parabolam eandem habeantur, posito rursus
Porro ut aequationes ad circumferentiam circuli, et ad parabolam eandem habeantur, posito rursus 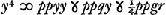 , auferatur utrinque ppyy + ttyy et dividatur per tt; fietque , auferatur utrinque ppyy + ttyy et dividatur per tt; fietque 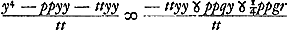 .
Jam ut ab altera parte, ubi est y4, fiat quadratum, addendum insuper ¼ quadrati ex .
Jam ut ab altera parte, ubi est y4, fiat quadratum, addendum insuper ¼ quadrati ex 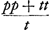 quod vocetur s. Itaque addito utrimque ¼ss, et aequata parte utrâque quadrato incognitae z, fiet quod vocetur s. Itaque addito utrimque ¼ss, et aequata parte utrâque quadrato incognitae z, fiet
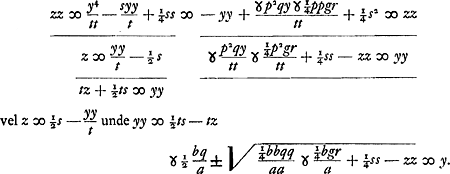 Altera aequatio ad parabolam cujus latus rectum t; altera ad circuli circumferentiam cujus radius 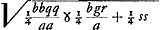 .
Quia autem in hyperbola simili inventus est axis .
Quia autem in hyperbola simili inventus est axis 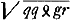 ; patet, si habeatur ; patet, si habeatur 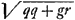 , vel si fuerit , vel si fuerit 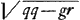 , dummodo qq sit majus quam gr, ad constructionem facere hyperbolam similem datae, ideoque et datam. Erit autem hic + gr, si in aequatione ∞ 0 fuerit + ¼ppgr, hoc est si ¼gg majus quam ¼aa + ee. , dummodo qq sit majus quam gr, ad constructionem facere hyperbolam similem datae, ideoque et datam. Erit autem hic + gr, si in aequatione ∞ 0 fuerit + ¼ppgr, hoc est si ¼gg majus quam ¼aa + ee.
Quomodo autem hyperbola data adhibeatur, etiam cum hic invenitur qq minus quam gr, postea ostendetur. In casibus vero jam dictis constructionem cum data hyperbola discemus, sicut in ellipsi, ex constructione cum hyperbola simili quam hic ipsa data referat. Ponatur aequatio y4 - ppyy + ppqy + ¼ppgr ∞ 0. Si OP recta referat | |
[pagina 352]
| |
axem parabolae cujus vertex 0, latus rectum t, oportet perpendicularem DO [Fig. 47] in axem parabolae a centro hyperbolae ductam cadere in ipsum verticem O, propter
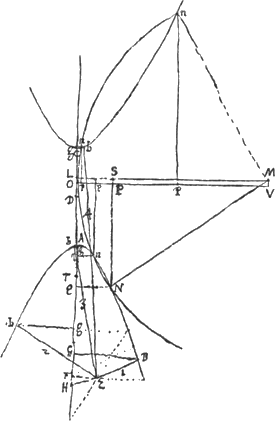 [Fig. 47].
aequationem ad parabolam vt ∞ yy. sunt enim OP ∞ v, PN ∞ y. Ipsa vero OD erit ½q, propter aequationem ad hyperbolen 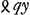 &c. Et patet haberi + qy, cum in aequatione ∞ 0 habeatur + ppqy, ut hic positum; ideoque OD accipiendam in partem affirmatam, hoc est in quam cadit y five TG sumpta à puncto T ubi terminatur ½g ∞ DT.
Rursus in constructione per circulum, oportet perpendicularem a centro circuli M abscindere portionem axis parabolae ad verticem, VO aequalem ½s, propter aequationem ad parabolam &c. Et patet haberi + qy, cum in aequatione ∞ 0 habeatur + ppqy, ut hic positum; ideoque OD accipiendam in partem affirmatam, hoc est in quam cadit y five TG sumpta à puncto T ubi terminatur ½g ∞ DT.
Rursus in constructione per circulum, oportet perpendicularem a centro circuli M abscindere portionem axis parabolae ad verticem, VO aequalem ½s, propter aequationem ad parabolam 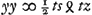 . est enim VP ∞ z. Ipsa vero perpendicularis MV erit ½ bq/a, sumenda in partem negatam, quia hic erit - ½ bq/a propter + ppqy in aequatione ∞ 0. adeo ut VM sive OL, et OD, semper cadant in partes contrarias.
Radius porro circuli MN erit . est enim VP ∞ z. Ipsa vero perpendicularis MV erit ½ bq/a, sumenda in partem negatam, quia hic erit - ½ bq/a propter + ppqy in aequatione ∞ 0. adeo ut VM sive OL, et OD, semper cadant in partes contrarias.
Radius porro circuli MN erit 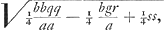 quia ¼ bgr/a debet habere signum contrarium ejus quod, in aequatione ∞ 0, praefixum est ¼ppgr. quia ¼ bgr/a debet habere signum contrarium ejus quod, in aequatione ∞ 0, praefixum est ¼ppgr.
Notetur vero quod OL + OD, hoc est ½ bq/a + ½q aequatur ½ hq/a quia h ∞ a + b. ut proinde DL sit ½ hq/a. Item VO sive ML, quae erat ½s, aequari ½ ht/a, quia s ∞ pp/t + t; et pp/t ∞ tb/a, quia pp/tt ∞ b/a. Et jam quidem perpendiculares NP ab intersectionibus N in rectam OP erunt ipsae radices y in hyperbola data adhibendae; quarum quae sunt a parte affirmata statuendae sunt in axe ejus hyperbolae a puncto T (ubi terminatur DT ∞ ½g), in partem affir- | |
[pagina 353]
| |
matam, velut TG; quae vero NP sunt à parte contraria, etiam a puncto T in contrariam partem accipiendae, ut Tg. Et excitatis (in hyperbola nimirum data) perpendicularibus GB, gb, invenientur omnia puncta B ad quae ductae a dato puncto E sint hyperbolae perpendiculares, quae quidem quatuor esse possunt at lineae notatae 1, 2, 3, 4. Jam porro ut Hyperbola data uti possimus et circulo ad easdem y in veniendas, reductio proportionalis facienda. Nempe augendus vel minuendus radius circuli, itemque rectae quae centrum ipsius definiunt, respectu centri D hyperbolae datae, secundum proportionem l ad a, ponendo l pro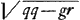 , quod aequale erat axi hyperbolae similis datae. Ergo DL quae erat ½ hq/a, jam erit ½ hq/l, accipienda in partem contrariam puncti F, quia in aequatione prima est + ppqy. Item LM, quae erat ½ h t/a, erit ½ ht/l. Et radius circuli fiet , quod aequale erat axi hyperbolae similis datae. Ergo DL quae erat ½ hq/a, jam erit ½ hq/l, accipienda in partem contrariam puncti F, quia in aequatione prima est + ppqy. Item LM, quae erat ½ h t/a, erit ½ ht/l. Et radius circuli fiet 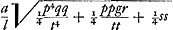 . DO vero, quam abscindit recta OP, cum fuerit ½q, erit jam ½ aq/l. Radices vero NP, hinc inventae erunt ay/l, quae reductae contraria proportione a ad l, dabunt radices veras y sive TG statuendas, ut diximus, à puncto T. Et haec constructio tantum adhibenda. Nam priorem idcirco proposui ut inventionis ratio perspiceretur. Sicut autem constructio haec quadrat illi quam in ellipsi dedimus ita et demonstratio eadem via procedit, nec fere nisi signis + et - differet. quamobrem hic omittetur.
Porro ut etiam casum illum de quo diximus, expediamus, ubi aequatio ad hyperbolam est . DO vero, quam abscindit recta OP, cum fuerit ½q, erit jam ½ aq/l. Radices vero NP, hinc inventae erunt ay/l, quae reductae contraria proportione a ad l, dabunt radices veras y sive TG statuendas, ut diximus, à puncto T. Et haec constructio tantum adhibenda. Nam priorem idcirco proposui ut inventionis ratio perspiceretur. Sicut autem constructio haec quadrat illi quam in ellipsi dedimus ita et demonstratio eadem via procedit, nec fere nisi signis + et - differet. quamobrem hic omittetur.
Porro ut etiam casum illum de quo diximus, expediamus, ubi aequatio ad hyperbolam est 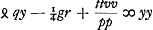 . ac proinde . ac proinde 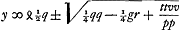 (minus autem qq quam gr). Sciendum hic designari locum ad hyperbolam in qua recta y ad axem ordinatim applicatur, cujusque latus rectum ad transversum ut tt ad pp ut facile est ostendere. Latus transversum verò, sive axis, fit (minus autem qq quam gr). Sciendum hic designari locum ad hyperbolam in qua recta y ad axem ordinatim applicatur, cujusque latus rectum ad transversum ut tt ad pp ut facile est ostendere. Latus transversum verò, sive axis, fit 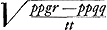 qui nunc vocabitur l. Ut vero haec hyperbola similis fiat hyperbolae datae, oportet tantum ponere tt ad pp sicut b ad a; cum priori casu fuerit tt ad pp ut a ad b. unde tantùm quantitas lineae t mutatur quae fiet ∞ √bpp/a. In aequatione autem ad circuli circumferentiam, observando item quod tt ad pp ut b ad a, invenietur qui nunc vocabitur l. Ut vero haec hyperbola similis fiat hyperbolae datae, oportet tantum ponere tt ad pp sicut b ad a; cum priori casu fuerit tt ad pp ut a ad b. unde tantùm quantitas lineae t mutatur quae fiet ∞ √bpp/a. In aequatione autem ad circuli circumferentiam, observando item quod tt ad pp ut b ad a, invenietur 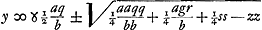 unde raduis circuli unde raduis circuli 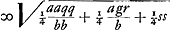 qui adhibendus cum hyperbola simili datae. qui adhibendus cum hyperbola simili datae.
Aequationes ad parabolam sunt eaedem quae priore casu. In constructione autem per hyperbolam et parabolam imaginariam, observandum | |
[pagina 354]
| |
hîc axem parabolae parallelum esse axi hyperbolae, quia eadem y ad utriusque axem ordinatim applicatur. Denique reductio omnium facienda ut prius secundum rationem l ad a.
Posita exempli gratia aequatione y4 - ppyy + ppqr - ¼ppgy ∞ 0 fiunt aequationes ad parabolam et ad hyperbolam similem datae 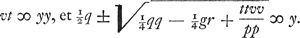 AEquationes autem ad parabolam et ad circumferentiam 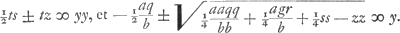 Eritque l, sicut dictum fuit, 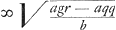 . Item . Item 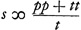 , hoc est ta/b + t, quia hic pp/tt ∞ a/b. Sed ta/b + t est ∞ th/b, quia h ∞ a + b. Ergo s jam erit ∞ th/b, t vero ∞ √bpp/a. Ex his igitur constructio oritur hujusmodi. , hoc est ta/b + t, quia hic pp/tt ∞ a/b. Sed ta/b + t est ∞ th/b, quia h ∞ a + b. Ergo s jam erit ∞ th/b, t vero ∞ √bpp/a. Ex his igitur constructio oritur hujusmodi.
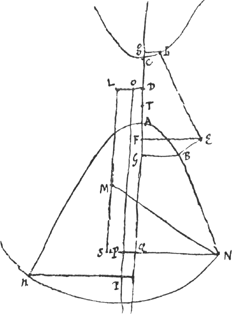 [Fig. 48]
A centro hyperbolae D [Fig. 48] erigatur axi perpendicularis DL ∞ ½ ahq/lb. idque in partem contrariam ejus ubi punctum E, quoniam in aequatione prima habetur + ppqy. Deinde sit LM, axi parallela, aequalis ½ aht/lb, accipienda in partem ubi est punctum F. Centro autem M, radio 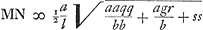 describatur circumferentia et à punctis N, ubi haec occurrit hyperbolae, cadant perpendiculares NP in rectam OP, axi parallelam, positâ DO ∞ ½aq/l. Sicut autem a ad l ita sint singulae NP, quae vocentur m, ad alias lm/a quae dicantur y. Ac denique posita in axe DT ∞ ½g, in partem ubi est E punctum, accipiantur ipsis describatur circumferentia et à punctis N, ubi haec occurrit hyperbolae, cadant perpendiculares NP in rectam OP, axi parallelam, positâ DO ∞ ½aq/l. Sicut autem a ad l ita sint singulae NP, quae vocentur m, ad alias lm/a quae dicantur y. Ac denique posita in axe DT ∞ ½g, in partem ubi est E punctum, accipiantur ipsis
| |
[pagina 355]
| |
lm/a aequales in axe TG, idque ita ut quae ortae sunt à perpendicularibus NP ad partes puncti E positis, cadant à T versus F, reliquae vero in partem contrariam. Jamque axi perpendiculares rectae GB ostendent in hyperbolis oppositis puncta B, ad quae, ductae ex puncto E, occurrant ipsis ad rectos angulos. Si ponatur axis AC seu a ∞ 2; latus rectum ∞ 1, DF sive c ∞ 3/2, FE sive d ∞ 3/2, fiunt h ∞ 3, g ∞ 1, pp ∞ 2, q ∞ ¼, gr ∞ ⅝. unde aequatio y4 - 2yy + ½y - 5/16 ∞ 0, in qua signa + et - conveniunt ijs quae paulo ante posuimus. Porro hic fit t ∞ 1, s ∞ 3, l ∞ 3/2 √½. Unde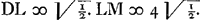 Radius Radius 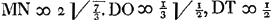
C § 6. Demonstratio Constructionis. Concurrant LM et NP in S, CA, NP in Q. Et ut a ad l ita sit DQ ad aliam quae dicatur v. eritque DQ ∞ av/l. Quia autem ut a ad l ita fecimus m ad y, erit m sive NP ∞ ay/l. Jam vero, propter hyperbolen, rectangulum CQA hoc est quadratum DQ minus quadrato DA, erit ad quadr. NQ, ut axis hyperbolae ad latus rectum, hoc est ut a ad b. Atqui quadr. DQ est aavv/ll. quadratum vero DA ∞ ¼aa. Quadratum denique NQ, hoc est ab NP minus DO, hoc est ab ay/l ½ aq/l, est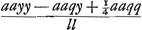 . Ergo ut hoc ad aavv/ll - ¼aa ita b ad a. unde aequatio existit, per quam invenitur . Ergo ut hoc ad aavv/ll - ¼aa ita b ad a. unde aequatio existit, per quam invenitur
vv ∞ ayy - aqy + ¼ aqq + ¼ bll, et restituto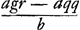 pro ll, fit pro ll, fit 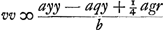 .
Jam porro ut a ad l ita MS ad aliam, quae dicatur z: Ergo MS ∞ az/l. Est autem, propter Circulum, quadratum MN aequale quadratis ab MS et SN. Sed quadr. MN est ¼ a4qq/llbb + ¼ a3gr/llb + ¼ aass/ll ex constructione; quadratum MS ∞ aazz/ll, quadratum vero SN, sive ab NQ + QS, est aayy/ll + a3qy/llb + ¼ a4qq/llbb. Nam si ad NQ, quae erat .
Jam porro ut a ad l ita MS ad aliam, quae dicatur z: Ergo MS ∞ az/l. Est autem, propter Circulum, quadratum MN aequale quadratis ab MS et SN. Sed quadr. MN est ¼ a4qq/llbb + ¼ a3gr/llb + ¼ aass/ll ex constructione; quadratum MS ∞ aazz/ll, quadratum vero SN, sive ab NQ + QS, est aayy/ll + a3qy/llb + ¼ a4qq/llbb. Nam si ad NQ, quae erat 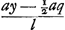 , addatur QS sive DL ∞ ½ahq/lb; hoc est , addatur QS sive DL ∞ ½ahq/lb; hoc est 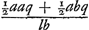 , quia h ∞ a + b; fiet NS ∞ ay/l + ½aaq/lb. Ergo hinc rursus aequatio existit, quae reducta relinquit zz ∞ ¼ agr/b + ¼ss - aqy/b - yy. , quia h ∞ a + b; fiet NS ∞ ay/l + ½aaq/lb. Ergo hinc rursus aequatio existit, quae reducta relinquit zz ∞ ¼ agr/b + ¼ss - aqy/b - yy.
| |
[pagina 356]
| |
Quia vero erat LM ∞ ½aht/lb ex constructione, hoc est ½ as/l, quia s erat ∞ th/b; DQ vero sive LS ∞ ay/l. erit 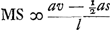 . Erat autem MS ∞ az/l. Ergo haec inter se aequalia, unde z ∞ v - ½s; et zz ∞ vv - vs + ¼ss. Sed erat zz ¼ agr/b + ¼ss - aqy/b - yy. Ergo hinc alia aequatio, ex qua sit . Erat autem MS ∞ az/l. Ergo haec inter se aequalia, unde z ∞ v - ½s; et zz ∞ vv - vs + ¼ss. Sed erat zz ¼ agr/b + ¼ss - aqy/b - yy. Ergo hinc alia aequatio, ex qua sit 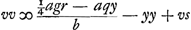 . Sed invenimus antea . Sed invenimus antea 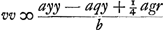 . Ergo alia rursus hinc aequatio. Ex qua invenitur ayy/b ∞ vs - yy, hoc est tv ∞ yy, quia s ∞ ht/b et h ∞ a + b. Itaque est v ∞ yy/t. Et proinde vv ∞ y4/tt. Sed erat . Ergo alia rursus hinc aequatio. Ex qua invenitur ayy/b ∞ vs - yy, hoc est tv ∞ yy, quia s ∞ ht/b et h ∞ a + b. Itaque est v ∞ yy/t. Et proinde vv ∞ y4/tt. Sed erat 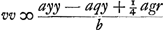 ; sive, restituto ; sive, restituto
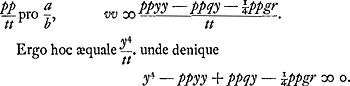 Quae cum sit aequatio eadem quae ex problematis analysi reperta erat, apparet recte se habere constructionem. C § 7. Aliter utroque casu. Sit rursus eadem quae supra aequatio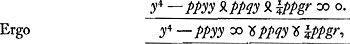 et addita utrinque ttyy et dividendo per pp fit 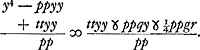 Ut autem ab altera parte fiat quadratum ubi est y4, addendum insuper ¼ quadrati ex 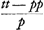 quod vocetur s, itaque addito utrimque ¼ss et aequata parte aequationis utraque quadrato incognitae v, fiet quod vocetur s, itaque addito utrimque ¼ss et aequata parte aequationis utraque quadrato incognitae v, fiet
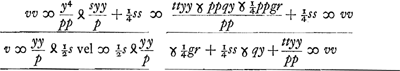 | |
[pagina 357]
| |
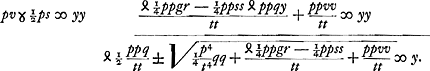 Quarum altera aequatio ad parabolam cujus latus rectum p, altera ad hyperbolen cujus latus rectum ad transversum ut tt ad pp quaeque proinde similis erit datae, ponendo pp/tt ∞ a/b, habebitque latus transversum 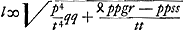 , nempe si in quantitatibus hac radice comprehensis signa + praevaleant signis -. Et tunc quidem linea y parallela intelligitur axi hyperbolae.
Sed si praevaleant in radice signa -, tunc locus designat hyperbolam cujus latus rectum ad transversum ut pp ad tt, quae, proinde, ut similis fiat hyperbolae datae, ponendum pp/tt ∞ b/a. Ejus vero latus transversum sive axis erit , nempe si in quantitatibus hac radice comprehensis signa + praevaleant signis -. Et tunc quidem linea y parallela intelligitur axi hyperbolae.
Sed si praevaleant in radice signa -, tunc locus designat hyperbolam cujus latus rectum ad transversum ut pp ad tt, quae, proinde, ut similis fiat hyperbolae datae, ponendum pp/tt ∞ b/a. Ejus vero latus transversum sive axis erit 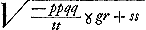 ; et recta y ad axem ordinatim applicata. Porro ad inveniendum locum ad circuli circumferentiam; cum sit ut prius ; et recta y ad axem ordinatim applicata. Porro ad inveniendum locum ad circuli circumferentiam; cum sit ut prius 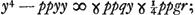 auferatur utrimque ppyy, et divisio fiat per pp, eritque auferatur utrimque ppyy, et divisio fiat per pp, eritque
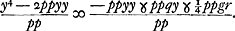 Insuper, ad formandum ab altera parte quadratum, addatur utrimque pp, et pars utraque aequetur quadrato incognitae z. fietque 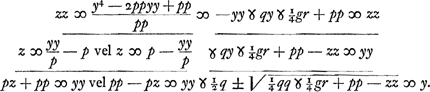 Quarum aequationum altera ad parabolam, cujus rursus latus rectum p. Altera ad circumferentiam cujus radius 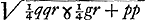 . Notandumque nullam hic utroque casu esse differentiam, nempe in definiendo circuli radio, quia scilicet + hic non habetur. . Notandumque nullam hic utroque casu esse differentiam, nempe in definiendo circuli radio, quia scilicet + hic non habetur.
Ut constructionis ratio utroque casu appareat, ponatur inventa aequatio y4 - ppyy + ppqy + ¼ppgr ∞ 0, et esse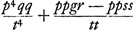 quantitatem affirmatam, et a majus quam b. Fient igitur aequationes ad parabolam et hyperbolam similem quantitatem affirmatam, et a majus quam b. Fient igitur aequationes ad parabolam et hyperbolam similem
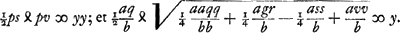 | |
[pagina 358]
| |
Aequationes vero ad parabolam et ad circumferentiam
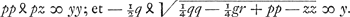 Item l erit 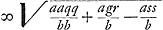 et s ∞ p - bp/a.
Hinc igitur primi casus constructio fiet hujusmodi. Ponatur DL [Fig. 49] in axe et s ∞ p - bp/a.
Hinc igitur primi casus constructio fiet hujusmodi. Ponatur DL [Fig. 49] in axe
 [Fig. 49].
in partem contrariam puncti F, quoniam in aequatione prima habetur + ppqy; sitque DL ∞ ½ahq/lb. Porro sit LM axi perpendicularis ∞ ½ap/l. Jam centro M radio 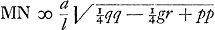 describatur circumferentia. Et a punctis quibus ea hyperbolae vel sectionibus oppositis datis occurrit, cadant perpendiculares in rectam OP, quae ponatur axi ad angulos rectos, sumptâ DO ∞ ½ aaq/lb. quae perpendiculares NP singulae vocentur m. Atque ut a ad l ita sit m ad aliam ml/a. ac denique sumto in axe intervallo DT versus F, quod sit ½g, accipiantur TG aequales singulis ml/a, idque ita ut quae TG sunt à perpendicularibus NP a parte puncti F positis, cadant ultra punctum T à centro D; reliquae vero in partem contrariam. Jamque axi perpendiculares GB ostendent puncta B, ad quae ductae ex puncto E occurrant hyperbolae ad angulos rectos. describatur circumferentia. Et a punctis quibus ea hyperbolae vel sectionibus oppositis datis occurrit, cadant perpendiculares in rectam OP, quae ponatur axi ad angulos rectos, sumptâ DO ∞ ½ aaq/lb. quae perpendiculares NP singulae vocentur m. Atque ut a ad l ita sit m ad aliam ml/a. ac denique sumto in axe intervallo DT versus F, quod sit ½g, accipiantur TG aequales singulis ml/a, idque ita ut quae TG sunt à perpendicularibus NP a parte puncti F positis, cadant ultra punctum T à centro D; reliquae vero in partem contrariam. Jamque axi perpendiculares GB ostendent puncta B, ad quae ductae ex puncto E occurrant hyperbolae ad angulos rectos.
Note ajoutée plus tard. 2 Oct. 1687. Inveni easdem constructiones hasce inveniri methodo Slusij; quae est in Mesolabo ejus pag. 92. si suppleantur in hac methodo quae ibi ad marginem annotavi. Et ex constructione per ellipsin aut hyperbolen datae similem, deducatur constructio per ellipsin aut hyperbolen datam, uti hic fecimus, quod Slusius non videtur animadvertisse semper fieri posse absque novo calculo. Itaque ipsius methodum huic nostrae praefero, magis intricatae. | |
[pagina 359]
| |
Cette remarque ajoutée en 1687 au texte du Manuscrit 11 s'accorde avec ce que l'on trouve à la p. 291 du Manuscrit F, datant également de 1687 (la p. 285 est datée août 1687 et la p. 311 3 déc. 1687): Aequationes meae problematis Apolloniani reductae ad locos secundum methodum Slusij pag. 92 Mesolabi.  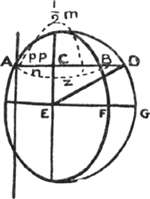 [Fig. 50].
Et restituendo ppnz pro ppyy fit aequatio ad parabolam | |
[pagina 360]
| |
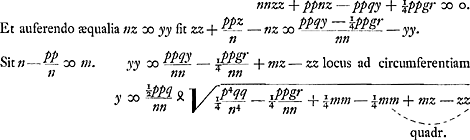 Ex his intellexi meam methodum construendi problema Apollonij de perpendiculari ex dato puncto in hyperbolam vel ellipsin ducenda eodem redire quo Slusij illa pag. 92 Mesolabi, quae non opus habet tantis ambagibus. Sed in ea supplendum quod ibi ad marginem notavi. |
|

