Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 330]
| |
Appendice II
| |
Problema Alhazeni ad inveniendum in superficie speculi sphaerici punctum reflexionis.Extat hoc problema in Alhazeni Arabis libris, quos de rebus opticis conscripsit, unde idem transcripsit, ut caetera fere omnia, VitellioGa naar voetnoot1). Est autem solutio ac demonstratio Alhazeni longa admodum ac tediosa, ipsumque problema difficile visum est geometris plerisque nec a quoquam postea brevius constructum quod sciam. Caeterum analyticae artis opera non uno modo illud resolvimus, quorum tandem hic quem tradimus, visus est omnium optimus brevissimusque. Sit ergo propositum dato circulo cujus centrum A, punctisque B, C, invenire in | |
[pagina 331]
| |
circonferentia punctum H [Fig. 40] ut ductae BH, HC occurrant circumferentiae ad
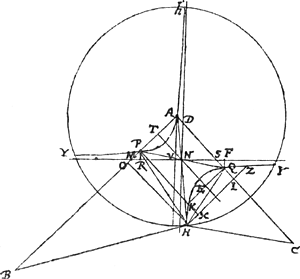 [Fig. 40].
angulos aequales, sive ut aequales sint anguli AHB, AHC. Sit factum, et ducatur HP ut sit angulus HPA aequalis BHA. Item ducatur HQ, ut angulus HQA sit aequalis CHA. Est ergo et angulus HQA aequalis HPA. Erunt vero similia triangula BHA, HPA, cum et angulum A commune habeant. Itemque similia erunt triangula CHA, HQA. Proportionales igitur BA, AH, AP; item CA, AH, AQ. cumque duae priores proportionalium utrobique datae sint, dabitur et tertia. Datae igitur AP, AQ. Vocetur jam AQ, a; AP, b. Ductâque HO parallelâ AC, et HI parallelâ AB, sit AI ∞ x: IH ∞ y. Erunt autem similia triangula HOP, HIQ, cum aequales habeant angulos ad O et I, itemque ad P et Q. Itaque ut HO ad OP ita HI ad IQ. Unde rectangulum HO, IQ, sive rectangulum AIQ aequale rectangulo HI, OP, sive rectangulo AOP. Est autem AI ∞ x; AQ ∞ a. Ideoque QI ∞ x - a. Et rectang. AIQ ∞ xx - ax. Est etiam AO sive IH ∞ y; AP ∞ b; unde OP ∞ y - b, ac proinde rectang. AOP ∞ yy - by. Itaque xx - ax ∞ yy - by. Unde patet, secundum regulas artis, punctum H esse ad hyperbolen; cujus latus transversum rectumque aequalia, siquidem in aequatione inveniuntur xx et yy nulla proportione affecta. Erit autem constructio hujusmodi. Applicato quadrato radij ad singulas AB, AC, fiant AP, AQ, super rectis AB, AC accipiendae; junctâque PQ dividatur ea aequaliter in puncto NGa naar voetnoot2). per quod ducatur recta DN parallela AV, quae angulum BAC aequaliter partitur. Ipsam vero ND ad N, recta alia ad rectos angulos secet, occurrens lineis AB, AC in M et S. Jam, asymptotis DN, NS, descriptae intelligantur hyperbolae oppositae per puncta P, Q transeuntes; quarum altera etiam per centrum A transibit. Hae secabunt circumferentiam in punctis H, h quaesitis ad quae nimirum ductae BH, HC propofitum efficient. | |
[pagina 332]
| |
Demonstratio. Ducantur enim PR, QF rectae NS perpendiculares. Quia ergo PN aequalis NQ ex constructione erit et PR aequalis QF. Similia autem sunt triangula PRM, QFS, propter aequales angulos M et S ex constructione. Ergo MR aequalis SF. Quare et MS aequalis RF. Sed MS dupla est VS: et RF dupla NF, propter aequales PN, NQ. Itaque et VS aequalis NF; ideoque et VN aequalis SF. Est autem sicut SF ad SQ, sive ut SN ad SD ita VN ad AD. Ergo AD aequalis SQ, ideoque punctum A est in sectione opposita ipsi QH sectioni, hoc est in eadem in qua et punctum P, per 16 lib. 2 ConicorumGa naar voetnoot3). Jam ducantur HO parallela AQ et HI parallela AP, occurrens sectioni in Z. Item jungantur AH, HP, HQ, et per N ducatur recta TNE parallela AQ; ea dividet AP aequaliter, quia PN aequalis NQ. Est ergo AP ordinatim applicata ad sectionis diametrum TNE. Quod si ducatur ipsi AP parallela QK, etiam haec diametro TNE ordinatim applicata erit, et ab ea proinde aequaliter dividetur in E. cumque QE sit aequalis AT, erit et tota QK aequalis AP. Quare si ducatur PK, ea erit parallela TE diametro. Conveniat autem cum recta HI in X. Cum igitur HXZ ad diametrum TE ordinatim sit applicata, quippe parallela AP ex constructione, sitque oppositarum sectionum latus rectum transverso aequale, ex prop. 22. lib. 3. ConicorumGa naar voetnoot4) rectangulum PXK aequale esse rectangulo HXZ, ac proinde PX ad XH, hoc est HO ad OP, ut XZ ad XK, hoc est ut HI ad IQ. Est enim XZ aequalis HI, quoniam IX et ZH utraque bisecantur à recta TE. Sunt ergo similia triangula HOP, HIQ, cum anguli ad O et I aequales sint. Quare etiam aequales anguli HPO, HQI: ac proinde et HPA, HQA. Atqui angulus HPA aequalis est BHA, quia similia sunt triangula BHA, HPA, propter proportionales BA, AH, AP ex constructione, angulumque utrique triangulo communem ad A. Similiterque angulus HQA aequalis CHA quia similia sunt triangula CAH, HAQ propter proportionales CA, AH, AQ. Ergo etiam aequales erunt anguli BHA, CHA. quod erat demonstrandum. Conveniunt autem tum constructio tum demonstratio, ijsdem verbis expressae, omnibus casibus, sive extra sive intra circulum puncta B, C data fint, sive alterum extra alterum intra. | |
[pagina 333]
| |
Et in casu quidem quem figura [Fig. 41] exhibet, etiam punctum h reflectit radium in superficie cava, ut ex B manans dirigatur ad C, vel vice versa. Reliquae vero intersectiones, circumferentiae et oppositarum hyperbolarum, ad YY [Fig. 40], hoc tantum
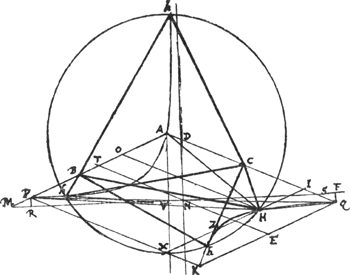 [Fig. 41]Ga naar voetnoot5).
praestant, ut radij, ex B vel C egressi, ita ibi reflectuntur ut respiciant punctum alterum, tanquam ex eo exijssent. At cum utraque puncta B, C intra circulum dantur, quatuor esse possunt vera reflexionis puncta [Fig. 41]. |
|

