Oeuvres complètes. Tome XX. Musique et mathématique

[p. 328]

Appendice I
À la pièce VIII de la p. 265 (Problema Alhaseni)
1672.

25 Maj. 1672.

Problema Alhaseni. Dato circulo cujus centrum A radius AD, et punctis duobus B, C. Invenio punctum H in circumferentia circuli dari, unde ductae HB, HC faciant ad circumferentiam angulos aequales.

Etc. C'est, peut-on dire, la Pièce que nous avons publiée dans le T. VII, p. 187-189 (pièce 1891). Comme on le voit dans ce Tome, elle fut envoyée de Paris par Huygens à Oldenburg dans une lettre du 1 juillet 1672. Les f. 136 et suiv. des Chartae mathematicae, auxquelles nous empruntons le présent Appendice, nous font connaître la date de la composition. Voyez aussi sur la pièce 1891 le premier alinéa de l'Appendice II qui suit.

Dans sa lettre Huygens a copié presque mot à mot la Pièce du 25 mai, mais il a omis la ‘ratio constructionis’ ou plutôt il ne l'a indiquée que dans trois lignes. Voici d'après la Pièce originale cette

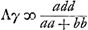
Ratio Constructionis (où il faut consulter les deux figures de la planche vis-à vis de la p. 187 du T. VII). Ducantur Pγ, Qζ perpendiculares in AM. Est ergo ut BA ad PA, hoc est, ut qu. BA ∞ aa + bb ad qu. IA ∞ dd, ita MA ∞ a ad , cui aequalem posuimus p. Ergo Aγ ∞ p. Sed ut AL ad AM ita CA ad AB, et ita PA ad AQ, (est enim ▭ BAP ∞ ▭^o CAQ, quia utrumque aequale qu.^o AD radij). Ut autem PA ad AQ ita Aγ ad Aζ. Ergo ut AL ∞ c ad AM ∞ a ita Aγ ∞ p ad Aζ ∞ ap/c. Quia autem R dividit bifariam rectam PQ, etiam o bifariam secabit γζ. Quamobrem AO erit ∞ ½ Aγ + ½Aζ, hoc est ∞ ½p + ½ap/c, cui aequalem posuimus s. Ergo AO ∞ s. Et OF ∞ x - s.

Porro ut AL ∞ c ad LC ∞ n ita est Aγ ∞ p ad γP, quae est pn/c. Item ut PA ad AQ hoc est ut CA ad AB, hoc est ut CL ∞ n ad MB ∞ b ita Pγ ∞ pn/c ad Qζ, quae ergo erit bp/c. Sed propter PQ bisectam in R, facile apparet esse OR ∞ ½ differentiae inter Qζ et Pγ. Ergo OR erit ½pb/c - ½pn/c, cui aequale posuimus q. Ergo OR sive FV ∞ q. Et VH ∞ y - q. Sed erat OF sive RV ∞ x - s. Ergo ▭ RVH ∞ xy-

[p. 329]

qx-sy + sq. Sed idem ▭ RVH ex constructione aequale est ▭^o AOR hoc est sq, nam AO est s et OR ∞ q. Ergo xy - qx - sy + sq ∞ sq, et ablatis aequalibus sit xy ∞ qx + sy ut in aequatione superius inventa. [Ergo] constat recte constructum esse problema.

Quod autem hyperbolae per puncta P, Q transeunt sic constabit. Si enim in aequatione superiori , fuerit x ∞ p ∞ Aγ, fiet et . Ergo a - c ad b - n ut p ad -y. Sed a - c est ad b - n ut a ad b, quia a ad b ut c ad n. Ergo a ad b ut p ad - y. Sed ut a ad b, hoc est, ut AM ad MB ita p sive Aγ ad γP. Ergo γP ∞ -y quand [sic] Aγ ∞ x. Unde liquet hyperbolam transire per punctum P. Itaque et per Q transibit hyperbola opposita quia PR ∞ RQ ex constructione. Estque R centrum oppositarum sectionum.

Ensuite Huygens considère quelques cas particuliers. Il biffa plus tard ces remarques au crayon, ne les jugeant sans doute pas fort importantes.

Voyez sur les solutions concurrentes de René de Sluse et de Huygens du problème d'Alhazen dans les années 1671 et 1672 les p. 218 et 219 (note 128) de l'Avertissement qui précède.