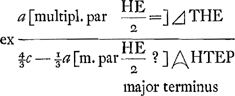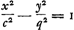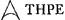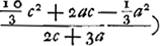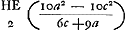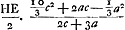Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 323]
| |||||||||||||
Appendice V
| |||||||||||||
[pagina 324]
| |||||||||||||
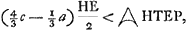 donc, comme dans le cas du cercle, un ‘terminus minor’.Ga naar voetnoot3) donc, comme dans le cas du cercle, un ‘terminus minor’.Ga naar voetnoot3)
| |||||||||||||
[pagina 325]
| |||||||||||||
 Ga naar voetnoot4) Ici aussi il y a chez Huygens erreur dans le cas de l'hyperbole. Il s'agit, comme dans le cas du cercle, d'un ‘terminus major’Ga naar voetnoot5). | |||||||||||||
[pagina 326]
| |||||||||||||
 Ga naar voetnoot6)Ga naar voetnoot7) Comme nous l'avons dit plus haut la première expression correspond au ‘terminus minor’ et la deuxième au ‘terminus major’. On voit tout de suite que la deuxième est supérieure à la première puisque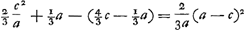 . .
| |||||||||||||
[pagina 327]
| |||||||||||||
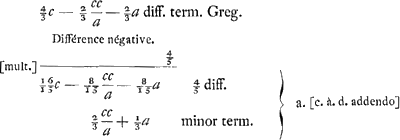 C'est au contraire un ‘terminus major’. L'addition ne donne donc pas, comme Huygens le pense, le terminus minor + ⅘ (t. major - t. minor), mais le t. minor + ⅕ de cette différence. 16/15c + 2/15 cc/a - 3/15 a approximatio Gregorij 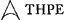 [c'est donc là l'approximation que Huygens appelle ‘approximatio Gregorij’ et dont il disait dans les paroles citées plus haut qu'elle est vraye ... dans l'hyperbole] quae erit minor terminus quippe minor etiam meo termino hic invento [voyez la note 7], ut constabit simili demonstratione ac pag. 4 [nos p. 312-316, démonstration se terminant par les mots: Et cum mea sit major vero et minor quam ipsius, erit et ipsius major vero] observando quod hic a major quam c [de sorte que (c - a)3 est négatif]. On voit en effet que la ‘demonstratio’ est ‘similis’ puisque l'approximation trouvée par Huygens (note 7) [c'est donc là l'approximation que Huygens appelle ‘approximatio Gregorij’ et dont il disait dans les paroles citées plus haut qu'elle est vraye ... dans l'hyperbole] quae erit minor terminus quippe minor etiam meo termino hic invento [voyez la note 7], ut constabit simili demonstratione ac pag. 4 [nos p. 312-316, démonstration se terminant par les mots: Et cum mea sit major vero et minor quam ipsius, erit et ipsius major vero] observando quod hic a major quam c [de sorte que (c - a)3 est négatif]. On voit en effet que la ‘demonstratio’ est ‘similis’ puisque l'approximation trouvée par Huygens (note 7) 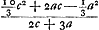 a exactement la même forme pour l'hyperbole que pour le cercle avec cette différence que cette expression constitue un ‘terminus major’ pour le cas du cercle, mais un ‘terminus minor’ pour celui de l'hyperbole.
Il importe peu que c et a soient ici, tant pour la formule 16/15 c + 2/15 cc/a - 3/15 a que pour la formule a exactement la même forme pour l'hyperbole que pour le cercle avec cette différence que cette expression constitue un ‘terminus major’ pour le cas du cercle, mais un ‘terminus minor’ pour celui de l'hyperbole.
Il importe peu que c et a soient ici, tant pour la formule 16/15 c + 2/15 cc/a - 3/15 a que pour la formule 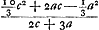 , d'autres grandeurs que dans les formules identiques de la p. 312 (comparez la note 2 de la p. 323). L'‘approximatio Gregorii’ est donc en effet, comme Huygens le dit, un ‘terminus minor’. , d'autres grandeurs que dans les formules identiques de la p. 312 (comparez la note 2 de la p. 323). L'‘approximatio Gregorii’ est donc en effet, comme Huygens le dit, un ‘terminus minor’.
|
|