Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 316]
| |
Appendice IVGa naar voetnoot1)
| |
[pagina 317]
| |
Il s'agit du Problema IV. Propos. XX du Traité de 1654 ‘De circuli magnitudine inventa’ (T. XII p. 172 et suiv.). Comme on peut le voir aussi dans le T. XII, Huygens n'a pas voulu publier la démonstration de cette proposition qui enseigne de trouver, en partant des limites supérieure et inférieure trouvées antérieurement, une limite inférieure plus exacte pour la longueur d'un arc. La limite qu'il calcule ici suivant cette proposition (dans son traité de 1654 il n'avait pas donné de formule algébrique), savoir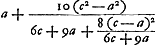 , correspond (lorsqu'on multiplie par 2n, nombre des côtés du polygone inscrit, dont AB = c est le côté) à la formule (terminus minor) de la note 52 de la p. 175 du T. XII, également déduite par nous de cette proposition, , correspond (lorsqu'on multiplie par 2n, nombre des côtés du polygone inscrit, dont AB = c est le côté) à la formule (terminus minor) de la note 52 de la p. 175 du T. XII, également déduite par nous de cette proposition,
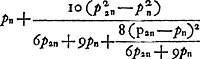 On peut voir aussi dans le T. XII que nous n'avons pas réussi à reconstruire la démonstration de la Prop. XX supprimée à dessein par Huygens et qui ne se trouve pas dans les manuscrits conservés. Per idem praeceptum ut summaGa naar voetnoot4) 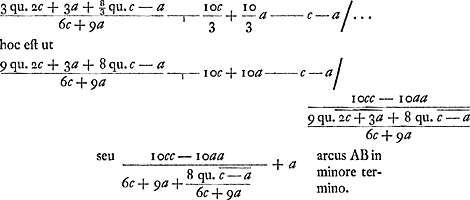 Major terminus ante inventus pag. 1Ga naar voetnoot5) hujus 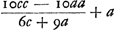 Ga naar voetnoot6). Ga naar voetnoot6).
Additiuncula ad a in majori ad additiunculam in minori termino ad eandem a, est vice versa ut hujus denominator ad illius denominatorem quoniam numerator utrobique idem. Ergo si additiuncula in majori sit HO, in minori HZ [Fig. 33]; erit | |
[pagina 318]
| |
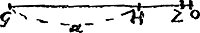 [Fig. 33].
HO ad HZ ut 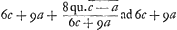 HO ad OZ ut
HO ad OZ ut 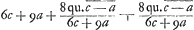 Hinc invento HO invenitur et HZ vel OZ.
HO ad OZ ut Hinc invento HO invenitur et HZ vel OZ.
HO ad OZ ut 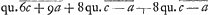 HZ ad ZO ut
HZ ad ZO ut 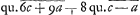 .
Cum ergo ut .
Cum ergo ut 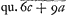 ad 8 qu. ad 8 qu. 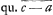 ita sit HZ ad ZO, hinc ostendo differentiam terminorum OZ non esse plurium quam duarum cifrarum si prior triens cifrarum constituentium a et c fit idem. Dicatur enim numerus ille, cifrarum utrobique earundem, s. Ergo tam a quam c habent cifras 3s et c - a non plures quam 2s, per Theor. 4Ga naar voetnoot7).
Demonstratio. Cum ergo 6c + 9a sit major numerus quam 10a; constat numerum factum additione 6c + 9a, habere non pauciores cifras quam 3s + unâ. Unde quadratum ab 6c + 9a non pauciores habebit quam 6s + unâ, per theor. 1 pag. 5 hujus. Sed c - a non habet plures quam 2s, per theor. 4 hujus. Ergo, quadratum ex c - a non habebit plures quam 4s et 8 qu. c - a non plures quam 4s + 1. Ruraus HZ cum sit minor utique quam dupla c - a, non habebit plures quam 2s + 1 per theor. 5 hujusGa naar voetnoot7). Ergo ducendo HZ in 8 ita sit HZ ad ZO, hinc ostendo differentiam terminorum OZ non esse plurium quam duarum cifrarum si prior triens cifrarum constituentium a et c fit idem. Dicatur enim numerus ille, cifrarum utrobique earundem, s. Ergo tam a quam c habent cifras 3s et c - a non plures quam 2s, per Theor. 4Ga naar voetnoot7).
Demonstratio. Cum ergo 6c + 9a sit major numerus quam 10a; constat numerum factum additione 6c + 9a, habere non pauciores cifras quam 3s + unâ. Unde quadratum ab 6c + 9a non pauciores habebit quam 6s + unâ, per theor. 1 pag. 5 hujus. Sed c - a non habet plures quam 2s, per theor. 4 hujus. Ergo, quadratum ex c - a non habebit plures quam 4s et 8 qu. c - a non plures quam 4s + 1. Ruraus HZ cum sit minor utique quam dupla c - a, non habebit plures quam 2s + 1 per theor. 5 hujusGa naar voetnoot7). Ergo ducendo HZ in 8 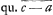 , productum non habebit plures quam 6s + 2. Et dividendo hoc productum per , productum non habebit plures quam 6s + 2. Et dividendo hoc productum per 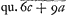 quod non pauciores habebat quam 6s + 1 habebit factus hinc hoc est OZ, non plures quam cifras 2, quantae fiunt cum à 6s + 2 aufertur 6s + 1, et rursus 1 additur per theor. 2 hujus. quod non pauciores habebat quam 6s + 1 habebit factus hinc hoc est OZ, non plures quam cifras 2, quantae fiunt cum à 6s + 2 aufertur 6s + 1, et rursus 1 additur per theor. 2 hujus.
Numquam igitur inter terminos approximationis meae majorem minoremque (sumtis utriusque cifris triplis numero ad multitudinem cifrarum similium in a et c, sinu et subtensa) poterit differentia major esse quam duarum cifrarum. plerumque vero ad unius quidem reperitur, sed tantum fractio aliqua, cum nempe amplius quam triplus verorum characterum numerus efficitur. Quae autem indicant fore minorem differentiam sunt haec. Ratio horum patet ex praecedente demonstratione. Si 6c + 9a habeat plures cifras quam 3s + 1, nam potest habere 3s + 2, si initiales in a et c sint magnae. et sic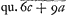 habebit 6s + 3 ut constat ex 1 theor. Rursus si c - a habeat initiales humiles ita ut habebit 6s + 3 ut constat ex 1 theor. Rursus si c - a habeat initiales humiles ita ut 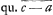 habeat tantum 4s - 1 cifras: simul enim fiet ut HZ, quae non est dupla c - a, tantum habeat 2s cifras. Haec humilitas cifrarum initialium in c - a cernitur in exemplo pag. 3Ga naar voetnoot8) unde ne unius quidem cifrae differentia inter terminos oritur ut videre licet in nostris de magnitudine circuli prop. 20Ga naar voetnoot9), ubi haec polygona adhibentur. habeat tantum 4s - 1 cifras: simul enim fiet ut HZ, quae non est dupla c - a, tantum habeat 2s cifras. Haec humilitas cifrarum initialium in c - a cernitur in exemplo pag. 3Ga naar voetnoot8) unde ne unius quidem cifrae differentia inter terminos oritur ut videre licet in nostris de magnitudine circuli prop. 20Ga naar voetnoot9), ubi haec polygona adhibentur.
| |
[pagina 319]
| |
Caeterum cum nostri termini hi major supra minorem possint differentiam habere duarum cifrarum, et Terminus ex nova approximatione pag. 8Ga naar voetnoot10) possit excessum habere supra majorem eorundem similiter duarum cifrarum. videndum jam quantum excessum habere possit Terminus iste ex nova approximatione supra Terminum minorem. Videretur dicendum prima fronte posse eum excessum esse 4 cifrarum. sed non potest esse plurium quam trium. Nam cum differentia inter minorem et majorem veterem non sit plurium quam 2 cifrarum, non erit major ista differentia quam 99. Et denuo cum differentia inter majorem veterem, et majorem novum sit non plurium quam 2 cifrarum nec major proinde quam 99, utraque differentia juncta, hoc est differentia inter minorem terminum et majorem novum non poterit esse major quam bis 99, sive 198; ideoque non major quam 3 cifrarum. Est vero pulchra quoque nova ista ApproximatioGa naar voetnoot10), quod, sicut vetusGa naar voetnoot11), triplum verarum notarum numerum in arcuum dimensione producit. nam uno ad summum ac plerumque ne uno quidem charactere aberrat, et quanquam pauxillo à veteri vincatur hoc exigui est momenti. Dat autem et constructionem egregiam ac simplicem, et ad numerorum calculum adhibita tantum opus habet latere inscripto, et circumscripto, et inscripto polygoni quod reliquorum numerum laterum subduplum habeat. Nam his datis, sola additione et subtractione arcus longitudinem verae proximam edit, adeo exacte ut si vel45o. gr. sit arcus non differat 1/25000 subtensae. Nempe si sinus sit a, subtensa hic erit arcus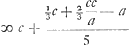 unde constructio erit hujusmodi. unde constructio erit hujusmodi.
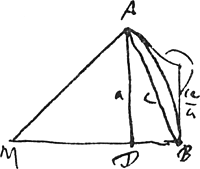 [Fig. 32].
VirijGa naar voetnoot12). 30 Sept. 1668. 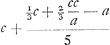 Approximatio nova. paulo major arcu cum a est sinus. c subtensa [Fig. 32]. ideoque cc/a latus polygoni circumscripti totidem laterum quot c. Approximatio nova. paulo major arcu cum a est sinus. c subtensa [Fig. 32]. ideoque cc/a latus polygoni circumscripti totidem laterum quot c.
| |
[pagina 320]
| |
Constructio.Datus fit arcus ABC cujus subtensa AC [Fig. 34]. Dividatur arcus bifariam in B et duplae subtensae AB ponatur aequalis AF. Ductâque BE perpendiculari in AB, ponatur duplae AE aequalis AG. Et sit GH tertia pars GF, et divisa HC in quinque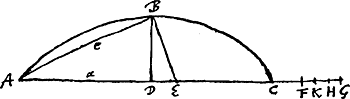 [Fig. 34].
aequales sit earum una FK. Et erit AF [lisez AK] aequalis arcui ABC, minimo excedens. Ratio constructionis. AG sit 2cc/a. AF est 2c. Ergo FG, 2cc/a - 2c. Et GH ∞ ⅔ cc/a - ⅔c. Qua ablata ab GA, 2cc/a fit HA ∞ 4/3 cc/a + ⅔c. Et CH ∞ 4/3 cc/a + ⅔c - 2a. Et hujus ⅕ nempe 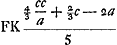 qua addita ad AF ∞ 2c, fit qua addita ad AF ∞ 2c, fit 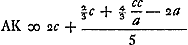 . .
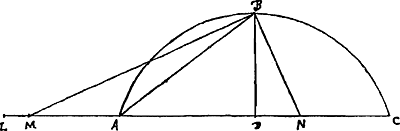
Constructio omnium accuratissima, et elegantissima ex approximatione veteri, 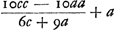 , noviter inventaGa naar voetnoot13). Sit datus arcus portionis ABC, cujus basis , noviter inventaGa naar voetnoot13). Sit datus arcus portionis ABC, cujus basis
 [Fig. 35].
| |
[pagina 321]
| |
AC diameter BD [Fig. 35]. In producta basi accipiatur AL aequalis ⅔ subtensae AB. Et minuatur DL parte sui decima LM. Ductaque recta MC, sit ei perpendicularis BN. Erit AN arcui AB aequalis, et dupla AN arcui ABC. Ratio constructionis quod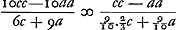 .
Est autem AD ∞ a, AB ∞ c, ideoque .
Est autem AD ∞ a, AB ∞ c, ideoque 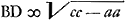 . Unde . Unde
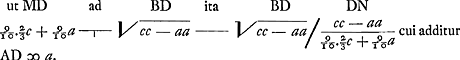 Haec constructio etsi in parvis arcubus parum excellat praecedentem, in magnis tamen arcubus multo praestantior est, nam etsi arcus ABC sit semicirculi, tamen dupla longitudo AN non excedet arcum ABC 1/1400 sui ipsius cum eo casu in priori constructione AK excedat arcum ABC amplius quam 1/370 suae longitudinis. Quod si vero ABC sit triens circumferentiae, jam in posteriori constructione, longitudo dupla AN non excedet arcum ABC 1/13000 sui parte. At si ABC sit circumferentiae quadrans, non erit excessus 1/90000 duplae AN. Rursus si ABC sit ⅛ circumferentiae, non erit excessus 1/5800000 duplae AN. Differentia inter subtensam et sinum est ad differentiam inter arcum et sinum ut sexcupla subtensa cum noncuplo sinu ad decuplum summae sinus et subtensae.
Vel Dato arcu circuli quadrante non majori, si fiat ut sexcupla subtensa cum noncuplo sinu, ad summam sinus subtensaeque ita eorundem differentia ad aliam, ejus decupla addita sinui efficiet longitudinem arcus.
Vel sic optime. Omnis circuli portionis, semicirculo non majoris, arcus aequalis est basi portionis et lineae quae sit ad diametrum portionis ut idem diameter ad novem decimas compo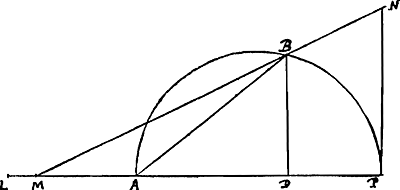 [Fig. 36]
| |
[pagina 322]
| |
sitae ex quadrante basis cum triente lateris trianguli maximi intra portionem inscripti.
Potest et eadem constructio variari hoc modo.
Sit datus arcus BP [Fig. 36] pars semicircumferentiae ABP, dimidia minor. Ducatur BD perpendicularis diametro AP. Et jungatur AB, ejusque duabus tertijs sumatur aequalis AL in producta diametro PA. totaque LD diminuatur parte sui decima LM, et jungatur MB et producatur occurratque tangenti circumferentiam ad P, in puncto N. Erit PN aequalis arcui PB. |
|