Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 310]
| |||||||
Appendice IIIGa naar voetnoot1)
| |||||||
[pagina 311]
| |||||||
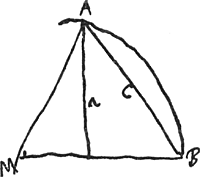
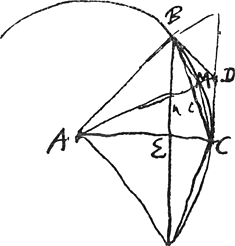 [Fig. 31].
Area polygoni ABC [Fig. 31] est BE ∞ a in AC. Pour trouver l'aire du polygone il faudrait évidemment encore multiplier par n/2, n étant le nombre des côtés.) Area polygoni totidem laterum ABDC est BDC ∞ cc/a in AC (même remarque). cc/a - a (ceci multiplié par AC, et par n/2, donne la différence des aires des polygones circonscrit et inscrit). Per Prop. 6 meam [du Traité nommé, savoir, dans la traduction française: Tout cercle est plus petit que les deux tiers du polygone semblable inscrit, T. XI, p. 130]:
Cette seconde équation correspond à la Prop. V (ou 5), T. XI, p. 128: Tout cercle est plus grand qu'un polygone à côtés égaux, qui lui est inscrit, plus le tiers de la quantité dont ce polygone surpasse un autre polygone inscrit d'un nombre de côtés réduit à la moitié.
Comme Huygens le dit dans la Pièce No. 1669 de notre T. VI (article publié dans le Journal des Sçavans du 12 nov. 1668) Gregory a en effet deux propositions équivalentesGa naar voetnoot2) aux Prop. V et VI de Huygens, de sorte qu'il trouve les mêmes valeurs supérieure et inférieure pour la surface du cercle (il faut toujours supposer les expressions ⅔cc/a + ⅓a etc. multipliées par le rayon AC et le nombre n/2; ou bien, ce qui est plus commode, supposer que le rayon a la longueur 1 et qu'il n'est pas question du cercle entier mais seulement d'un secteur). La différence de ces limites supérieure et inférieure est donc une ‘differentia Gregorij’ tout aussi bien qu'une ‘differentia Hugenii’. | |||||||
[pagina 312]
| |||||||
 D'après Huygens (voyez aussi la p. 274 du T. VI) Gregory croit obtenirGa naar voetnoot4) une nouvelle fort bonne approximation (il s'agit apparemment d'un ‘terminus major’) pour le secteur considéré en ajoutant à l'ancien ‘terminus minor’ seulement les ⅘ de la différence entre l'ancien ‘terminus major’ et l'ancien ‘terminus minor’. Huygens dit à la page citée (c.à.d. dans l'article du 12 novembre 1668 dont il était déjà question plus haut) ‘que cette approximation n'est pas vraye dans le cercle’Ga naar voetnoot5), c.à.d. qu'elle est beaucoup moins bonne que Gregory le pense, (à la p. 41 Huygens écrit: hanc approximationem Gregorius proponit sed inutilis est cum non accedat ad verum), puisqu'on obtient déjà un ‘terminus major’ en ajoutant non pas ⅘ mais ⅕ de la dite différence (voyez aussi sur ce sujet la première note de l'Appendice V qui suit), ce qui donne 2/15 cc/a - 3/15a +16/15c. Le rayon ayant par hypothèse la valeur 1, ce ‘terminus’ pour le ‘sector ABM’ peut tout aussi bien être appelé un ‘terminus’ pour l'arc BC de la même Fig. 31. Huygens peut donc le comparer avec son ‘terminus major’ à lui (le ‘terminus major’ de la Prop. XIX, plus exact que 2/3 c2/a + 1/3a) pour le même arc. Ce faisant il constate que 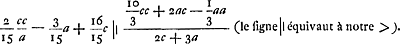 En effet, en multipliant par 2c + 3a, puis par 15/4a, il obtient 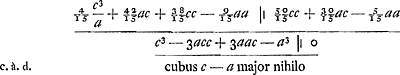 | |||||||
[pagina 313]
| |||||||
ce qui est évidemment exact (première ligne de la p. 275 du T. VI). Il conclut: Et cum mea sit major vero et minor quam ipsius, erit et ipsius major veroGa naar voetnoot6). Notons que Gregory dans sa lettre à Oldenburg du 25 décembre 1668, publiée dans les Philosophical Transactions du 15 février suivant (notre No. 1682, T. VI), nie (p. 309) que Huygens, en faisant cette observation sur la valeur de l'approximation obtenue par l'addition des ⅘ de la différence susdite, ait bien compris ce qu'il voulait dire.
§ 2. Parlant de l'approximation exprimée par l'expression 2/15 cc/a - 3/15a + 16/15c, Huygens dit dans le 4ième alinéa de la p. 274 du T. VI pouvoir démontrer que les polygones [inscrit et circonscrit] s'accordant jusqu'au tiers de leurs chiffres, [l'expression considérée] ne peut differer au plus de la veritable grandeur du cercleGa naar voetnoot7) que dans les deux derniers chiffres; et que le plus souvent il doit avoir tous les mesmes et au delà. Ceci n'est guère compréhensible pour le lecteur qui ne connaît pas le raisonnement de HuygensGa naar voetnoot8). Cette demi-obscurité est peut-être voulue. Quoi qu'il en soit, il ne semble pas inopportun de faire connaître le dit raisonnement. A la page 44 du Manuscrit D Huygens commence par établir les six théorèmes suivants, tous bien simples et dont il ne formule donc pas la démonstration. | |||||||
Theor. 1.Si numerus in numerum ducatur, habebit productum non plures cisras quam summa cifrarum eorum qui ducti sunt. Idem vero productum non pauciores habebit cifras quam summa cifrarum ductorum minus unâ. | |||||||
Theor. 2.Si numerus per numerum minorem dividatur, habebit quotiens non pauciores cifras quam differentia cifrarum eorundem numerorum, non plures vero quam eadem differentia cifrarum plus unâ. | |||||||
Theor. 3.Si duo numeri aequali numero cifrarum priores aliquot cifras easdem habuerint et proxima ab illis cifra majoris excedat binario vel amplius cifram suppositam minoris, | |||||||
[pagina 314]
| |||||||
auferaturque minor numerus à majore. habebit residuum totidem cifras quot erant in alterutro numero dissimiles. | |||||||
Theor. 4.Si duo numeri aequalem multitudinem cifrarum habuerint et priores aliquot cifras easdem alter alteri. ablato minore a majori, reliquus non habebit plures cifras quam quot erant cifrae dissimiles in ijsdem numeris. | |||||||
Theor. 5.Si duo numeri alter alteri addantur, summa non habebit plures cifras quam major numerorum plus unâ. quod autem non pauciores habebit quam major numerus, certum est. | |||||||
Theor. 6.Si numeri alicujus cifra initialis sit 1 vel 2, ejus quadratum cifras habebit bis tot quot latus cifras habebat minus una.
Ensuite, à la p. 47 du même Manuscrit, Huygens raisonne comme suit. Differentia terminorum majorum Gregorij correcti, et mei (voyez le § 1 qui précède) 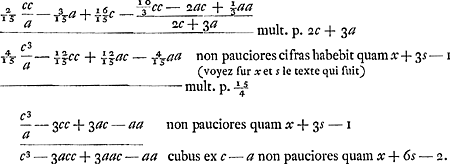 Dico autem quod si numeri c et a habeant priorem tertiam partem cifrarum eandem, sicut essent 104.671912 ∞ c et 104.528463 ∞ a quod tunc terminus istorum alter alterum non superabit numero ultra quam ex duabus cifris constante. Ponatur enim differentia eorum habere cifras x, et numerus cifrarum similium in numeris c et a, vocetur s. Ergo tam c quam a habent singuli cifras 3s. Quia ergo 2c + 3a non habet pauciores cifras quam 3s, sequitur ducendo ut fecimus 2c + 3a in differentiam propositam, productum non habiturum pauciores quam x + 3s - 1 per theorema 1 folii antepenultimi. Quod productum rursus ducendo in 15/4, jam illud quod oritur quoque non pauciores habebit quam x + 3s - 1 quia multiplicatio per 15/4 non potest minuere numerum cifrarum. Rursus multiplicando per a qui | |||||||
[pagina 315]
| |||||||
habet 3s cifras. productum non habebit pauciores quam x + 6s - 2 per theor. 1. Atqui hoc productum est cubus ab c - a. Ergo cubus ab c - a non habet pauciores quam x + 6s - 2. Ergo vicissim x + 6s - 2 non habet plures quam cubus ab c - a. Atqui cubus c - a non habet plures quam 6s, per 1 theor. Ergo x + 6s - 2 non habebit etiam plures quam 6s. Ergo x + 6s non habebit plures quam 6s + 2. Ergo x non plures quam 2. Argumentatio subtilis. |
|


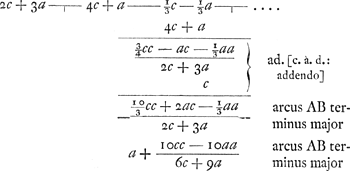
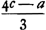 ), qu'une limite supérieure du même arc, celle considérée ici. Les mots ‘arcus AB terminus major’ signifient donc que la quantité
), qu'une limite supérieure du même arc, celle considérée ici. Les mots ‘arcus AB terminus major’ signifient donc que la quantité 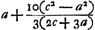 est supérieure à la longueur de l'arc.
est supérieure à la longueur de l'arc.