Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 308]
| |
Appendice IIGa naar voetnoot1)
| |
[pagina 309]
| |
que de dire que nul secteur de cercle ne l'est. Qui dit non omnis ne dit pas nullus. Et ainsi il ne suffit pas de demonstrer que le secteur de cercle a sa figure inscrite n'est pas analytique indefinitè, mais il faut demonstrer que c'est la mesme chose in casu omni definito. comme par exemple quand on prend le secteur qui fait le tiers du cercle, supposant a egal a 1, b ∞ 2: les premiers termes de sa suite convergente seront 3 et 12, les seconds 6 en 8. Que si je disois maintenant que la terminaison de cette suite est .... ou √......, je ne pense pas que par sa prop. 11 il me puisse prouver le contraire. Par consequent il ne s'en suit pas de ses demonstrations que le cercle ne soit au triangle equilateral inscrit comme nombre a nombre. La mesme chose sera vraie dans tous les secteurs dont la soutendente au rayon du cercle aura quelque raison donnee de nombre a nombre soit rationel soit sourd. car depuis qu'entre les quantitez a et b dans sa prop. 11 il y aura proportion numerique, l'on ne pourra plus dire de quelle sacon un autre nombre proposè est composè des premiers ny des seconds termes de la suite convergente. Et par consequent en tous ces cas la propos. 11 ne demonstre point qu'il soit impossible de trouuer la terminaison par quelque autre methode que celle de l'autheur. Et c'est ce qui justifie ma premiere remarque. Pour les autres il est vray qu'elles sont toutes fondees sur ce que l'autheur n'avoit point limitè l'usage de la methode dont il cherche la terminaison dans la 7 prop. ny fait la declaration qu'il fait maintenant en ces mots. Dico igitur et declaro me intelligere nullam quantitatem indefinitam praeter ipsos terminos convergentes compositionem posse ingredi. Et si je n'avois eu sujet de croire qu'il eut ignorè cette rejection des quantitez indefinies, je ne me serois point arrestè a en faire veoir la necessitè, par les fausses consequences qui naissent de son omission. Mais puis que dans sa prop. 7e il faisoit entrer dans la composition la quantitè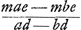 , ou les lettres a et b marquent des quantitez indefinies, j'ay eu raison d'en conclure qu'il les y avoit laissèes quoy que les scachant estre telles. Car necessairement l'un des deux est vray, ou qu'il ait essaiè d'oster a et b de cette quantitè ou qu'il ne l'ait point essaiè. S'il l'a essayè, il faut qu'il n'aye pas veu qu'il les pouvoit oster en divisant pas a - b car s'il l'eut veu, il ne pouvoit plus negliger cette division par inadvertance. N'ayant donc point veu que a et b se pouvoient oster apres l'avoir tentè, il a creu estre obligè d'admettre d'autres quantitez indefinies dans la composition, outre les termes convergents eux mesmes. Que s'il n'a point essaiè d'oster a et b, qu'il scavoit denoter des quantitez indefinies, il s'en suit qu'en les laissant il n'a pas seulement pensè que de telles quantitez ne deussent point entrer dans la composition. Et ainsi je pense avoir assez prouvè que ce ne sont pas mes seules imaginations comme il luy
plait dire qui ont donnè sujet
a mes dernieres objections. Mais quoy qu'il en soit cela ne fait plus rien a la question principale, qui est si M. Gregorius a demonstrè, comme il pretend, que la raison du cercle au quarrè de son diametre n'est pas analytique. , ou les lettres a et b marquent des quantitez indefinies, j'ay eu raison d'en conclure qu'il les y avoit laissèes quoy que les scachant estre telles. Car necessairement l'un des deux est vray, ou qu'il ait essaiè d'oster a et b de cette quantitè ou qu'il ne l'ait point essaiè. S'il l'a essayè, il faut qu'il n'aye pas veu qu'il les pouvoit oster en divisant pas a - b car s'il l'eut veu, il ne pouvoit plus negliger cette division par inadvertance. N'ayant donc point veu que a et b se pouvoient oster apres l'avoir tentè, il a creu estre obligè d'admettre d'autres quantitez indefinies dans la composition, outre les termes convergents eux mesmes. Que s'il n'a point essaiè d'oster a et b, qu'il scavoit denoter des quantitez indefinies, il s'en suit qu'en les laissant il n'a pas seulement pensè que de telles quantitez ne deussent point entrer dans la composition. Et ainsi je pense avoir assez prouvè que ce ne sont pas mes seules imaginations comme il luy
plait dire qui ont donnè sujet
a mes dernieres objections. Mais quoy qu'il en soit cela ne fait plus rien a la question principale, qui est si M. Gregorius a demonstrè, comme il pretend, que la raison du cercle au quarrè de son diametre n'est pas analytique.
|
|

