Oeuvres complètes. Tome XX. Musique et mathématique

[p. 288]

XIII. Théorème sur les points d'intersection des coniques dont les axes sont parallèles ou à angles droits.
Le théorème principal est précédé par deux autres propositions qu'on peut considérer comme des lemmes.
1680¹⁾.

Registres, T. IX, f. 32: Le Samedy 23 de Mars 1680 ... M^r Hugens a donné le théorème suivant touchant les sections coniques.

(Le brouillon du Manuscrit E - voyez l'Appendice - porte la date du 22 mars 1680.)

Theoreme. Si une section conique coupe une autre section conique en 4. points, et que leurs axes soient paralleles ou a angles droits l'un a l'autre ces quatre points seront dans la circonference d'un cercle. Les hyperboles opposees sont comptees pour une section.

D'ou sensuit que si une section conique coupe une parabole en 4 points ayant leur axes paralleles ou a angles droits l'un a l'autre, la somme des perpendiculaires, qui tombent des points d'intersection sur l'axe de la parabole d'un, et d'autre costé seront egales, ou l'une perpendiculaire d'un costé aux trois de l'autre.

Registres, T. IX, f. 33-35: Le Samedy 30^e de Mars [1680] M^r Hugens a donné la demonstration du Theoreme qu'il auoit proposé des sections coniques qui se coupent en 4. points dont suit la copie.

1) Comparez la note 5 de la p. 284 du T. VIII.
Voyez sur la publication de la Pièce XIII par F. Schuh en 1921 le début de la partie B de l'Appendice.

1^re Proposition.

Si une parabole est coupée par une section conique en 4 points, et que leur axes soient paralleles ou a angles droits l'un a l'autre les perpendiculaires menées des 4 points d'intersection sur l'axe de la parabole d'un costé et d'autre, auront leurs sommes egales, ou l'un d'un costé sera esgale aux trois de l'autre costé.

Cecy se demontre facilement par Algebre, parce qu'en mettant pour inconnue l'une de ces perpendiculaires, il paroit qu'on parvient necessairement a une equation quarréquarrée, ou manque le second terme sçauoir celuy qui est affecté sous le cube, d'ou l'on sçait que les valeurs affimées de cette inconnue sont ensemble egales aux valeurs negatiues de la mesme, c'est a dire les perpendiculaires d'un costé ensemble egales a celles de l'autre costé, ou l'une aux trois²⁾.

2) La parabole étant représentée par l'équation y² = 2px, l'ellipse ou hyperbole ayant un de ses axes parallèle à celui de la parabole s'écrira (nous nous servons d'équations de formes modernes) En éliminant x, on trouve en effet une équation du 4^ième degré en y où manque le terme en y³. Il en résulte que la somme algébrique des quatre valeurs d' y qui satisfont à cette équation est nulle; or, ce sont là les quatre perpendiculaires des points d'intersection des deux coniques sur l'axe de la parabole. Il en est de même lorsque la deuxième conique est une parabole dont l'axe est parallèle à celui des y.

[p. 289]

2^e Proposition.

Par trois points donnez qui ne soient pas en une ligne droite, l'on peut decrire une parabole dont l'axe soit parallele a une ligne donnée, pourveu que les points soient donnez en sorte, que des paralleles qu'on menera de chacun a la ligne donnée, il n'y en ait point de coincidentes.

Ce probleme se construit aisement par la conuerse de la 49^e du 1. Livre des Coniques³⁾.

3) Apollonios, Conica I, prop. 49 (d'après le texte latin de l'édition de I.L. Heiberg, Lipsiae, Teubner, 1891): ‘Si recta parabolam contingens cum diametro concurrit, per contactum autem recta diametro parallela ducitur, a uertice autem recta ordinate ductae parallela, et fit, ut pars contingentis inter ordinate ductam punctumque contactus posita ad partem parallelae inter punctum contactus et ordinate ductam positam, ita recta aliqua ad duplam contingentis, quaecunque recta a sectione [contingenti parallela] ad rectam per punctum contactus diametro parallelam ductam ducitur, quadrata aequalis est rectangulo comprehenso recta adsumpta rectaque ab illa ad punctum contactus abscisa’. La ‘recta adsumpta’ est le double paramètre 2p′ de l'équation y′² = 2p′x′ de la parabole par rapport à des axes obliques conjugués (diamètre et tangente). On peut en effet déduire du théorème énoncé que lorsque la direction du diamètre et trois points de la parabole sont donnés, celle-ci est déterminée; la construction du paramètre peut être effectuée.

3^e Proposition.

[Fig. 23].

Si deux sections coniques se coupent en 4 points, et que leurs axes soient paralleles ou a angles droits l'un a l'autre, les 4 points d'intersection sont dans la circonference d'un cercle.

Les hyperboles opposees sont comptees pour une section.

Soient deux sections coniques [Fig. 23] dont les axes EF, GH soient paralleles ou a angles droits et les 4. points de leur intersection A, B, C, D, je dis qu'ils sont dans la circonference d'un cercle.

[p. 290]

Demonstration.

Il y aura tousjours necessairement 3. de ces points situez en sorte qu'on puisse decrire une parabole par les trois, de laquelle l'axe soit parallele a l'axe de l'une des sections coniques données; ou bien les quatre points constitueront un rectangle, et ainsi ils seront manifestement dans la circonference d'un cercle. Soient les trois points A, B, C [Fig. 23 bis] et la parabole decrite CAB laquelle coupera necessairement chacune des sections donnees dans un quatrieme point, et je dis que ce point sera D, ou ces deux sections se coupent entr'elles.

Car puisque la parabole coupe la section GH, les perpendiculaires menées des points A, B, C et du 4^e point d'intersection sur l'axe de la parabole auront leurs sommes egales de part et d'autre par la 1.^re proposition. Et puisque la mesme parabole coupe la section EF les mesmes perpendiculaires des points A, B, C sur l'axe de la parabole, et celle du 4^e point d'intersection auront encore leurs sommes de part et d'autre egales, donc cette 4^e perpendiculaire est necessairement la mesme pour l'intersection de la parabole auec les deux sections GH et EF puisqu'il n'y a pas deux appliquées de mesme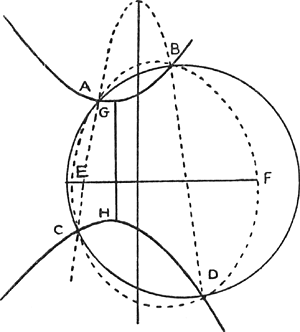

[Fig. 23 bis]

longueurs sur l'axe de la parabole, et du mesme costé, donc les points d'intersection de la parabole auec les deux sections coniques outre les intersections A, B, C conuiennent en un et par consequent ce point est D ou les deux sections s'entrecouppent.

Mais un cercle passant par les points A, B, C [Fig. 23 bis] doit aussi couper la parabole en un 4^e point en sorte que les appliquées de ce point et des points A, B, C sur l'axe de la parabole aient leurs sommes egales de part et d'autre. donc ce 4^e point est encore le mesme ou la parabole coupoit les deux sections sçauoir le point D et ainsi il paroit que les 4 points A, B, C, D sont dans la circonference d'un cercle.