Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 291]
| |
Appendice IGa naar voetnoot1)
| |
[pagina 292]
| |
aa/b - a; aa/b - a + a; aa/b - a + a + b; aa/b - a + a + b + bb/a; aa/b - a + a + b + bb/a + b3/aa... quarum ab ultima si auferatur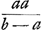 patet residuum aequari summae proportionalium quaesitae. patet residuum aequari summae proportionalium quaesitae.
per Logarithmos. A duplo logaro. termini minoris auferatur logs. differentiae inter terminum minorem et sequentem, et habebitur logar.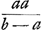 . Residuo addatur logar. proportionis datae, hoc est differentia log.orum termini minoris et sequentis sive quorumlibet duorum continue sequentium, multiplicatus per numerum multitudinis terminorum. Summa erit logar. numeri, a quo numero si auferatur numerus logarithmi . Residuo addatur logar. proportionis datae, hoc est differentia log.orum termini minoris et sequentis sive quorumlibet duorum continue sequentium, multiplicatus per numerum multitudinis terminorum. Summa erit logar. numeri, a quo numero si auferatur numerus logarithmi 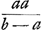 ante inventi; relinquitur summa proportionalium quaesita. ante inventi; relinquitur summa proportionalium quaesita.
§ 2. Iisdem datis, invenire proportionalium summam triangularem incipiendo a minima. 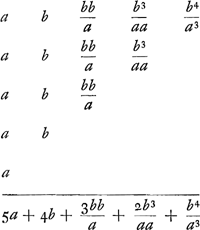 Cum sint proportionales supra inventae 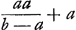 ; ; 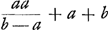 ; ; 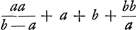 ; ; 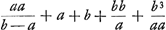 ;....
idque in ratione a ad b. inveniatur earum summa per praecedentem. ab qua si auferatur ;....
idque in ratione a ad b. inveniatur earum summa per praecedentem. ab qua si auferatur 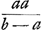 toties quot sunt termini, facile apparet residuum fore summam triangularem quaesitam.
§ 3. Aliter. Proportionalium a, b, bb/a &c summa per praeced. reperta vocetur s. Cum itaque in eadem proportione a ad b sint quoque proportionales aeque multae toties quot sunt termini, facile apparet residuum fore summam triangularem quaesitam.
§ 3. Aliter. Proportionalium a, b, bb/a &c summa per praeced. reperta vocetur s. Cum itaque in eadem proportione a ad b sint quoque proportionales aeque multae 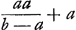 ; ; 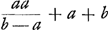 ; &c. erunt ut a ad s ita ; &c. erunt ut a ad s ita 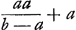 ad summam omnium posteriorum. sive permutando ut a ad ad summam omnium posteriorum. sive permutando ut a ad 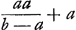 , hoc est, ut b - a ad b ita s ad summam omnium posteriorum, a qua si auferatur , hoc est, ut b - a ad b ita s ad summam omnium posteriorum, a qua si auferatur 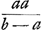
| |
[pagina 293]
| |
ductum in numerum terminorum, relinquitur ut ante summa triangularis proportionalium a, b, bb/a &c. incipiendo ab a. § 4. Prima propositio aliter. 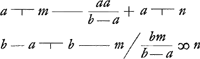 Sit m maxima proportionalium: a minima; b quae proxime post a sequitur. s summa proportionalium a, b, bb/a &c. n maxima proportionalium seriei 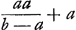 , , 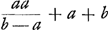 &c. Quum sint in prima propositione proportionales &c. Quum sint in prima propositione proportionales 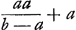 ; ; 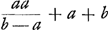 ; &c. totidem quot a, b, bb/a &c. et in ratione eadem a ad b patet esse sicut a ad maximam proportionalium a, b, bb/a &c. ita ; &c. totidem quot a, b, bb/a &c. et in ratione eadem a ad b patet esse sicut a ad maximam proportionalium a, b, bb/a &c. ita 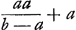 ad maximam sui ordinis n. A qua si auferatur ad maximam sui ordinis n. A qua si auferatur 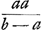 , fit (ut ex eadem prima propositione patet) residuum , fit (ut ex eadem prima propositione patet) residuum 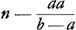 aequale summae s proportionalium a, b, bb/a &c. Sed aequale summae s proportionalium a, b, bb/a &c. Sed 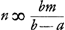 . Ergo . Ergo 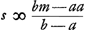 . .
§ 5. Secunda aliter. Erat b - a ⫟ b - s ⫟ summam posteriorum. 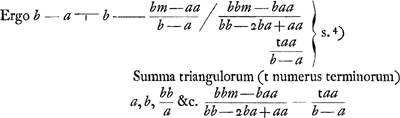 § 6. Si series proportionalium ab a infinitè parva incipere ponatur sive, ab m maxima, deorsum continuári in infinitum, patet ex regulis praecedentibus, cum a ad m infinite parvam rationem habeat, fore summam omnium in infinitum proportionalium 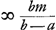 . Item summam triangularem omnium . Item summam triangularem omnium 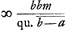 . .
| |
[pagina 294]
| |
§ 7. Tegen hoeveel ten hondert in 't jaer soudemen sijn gelt moeten beleggen, mids oock interest van interest ontfangende, om ten eynde van 41 jaer 3 capitalen boven het sijne te winnen? Antwoord: tegen 3 en 44/100 per cento. Omdat in als 4 capitalen moeten sijn, welcke 4 capitalen maecken de grootste van 42 proportionalen, daer de cleynste van is 100 en de grootste 400, soo divideer ick de differentie der logarithmi van 400 en van 100, te weten 0,60206, door 41, en de quotiens 1468 addeer ick tot de logar. van 100. komt 2,01468, sijnde logar. van 103,44. daerom is het capitael metten interest ten eynde vant eerste jaer 103, 44/100. En dienvolgens den interest van 100 in een jaer, 3 44/100. Ick heb gesegt 42 proportionalen om dat die 41 differentien maecken.  [Fig. 25].
La figure donnée par Huygens pour illustrer le texte [Fig. 25] fait voir que, tout aussi bien que Zarlino (note 1 de la p. 171 qui précède) et Mersenne (p. 33 qui précède, l. 2 d'en bas), il se figure comme des lignes les moyennes proportionnelles qu'il s'agit d'intercaler entre les deux quantités données. Il est évident que si la figure était correctement tracée les extrémités des lignes verticales équidistantes ne se trouveraient pas sur une ligne droite mais sur une logarithmique comme dans la Fig. 24 du § 1. La même remarque s'applique à quelques figures du même genre dans la ‘Chilias Logarith morum’ de 1624 de Kepler, ouvrage que Huygens ne mentionne d'ailleurs nulle part. Les pages suivantes du Manuscrit contiennent encore plusieurs autres calculs, également rédigés en flamand, sur des capitaux placés à intérêt; il y est fait usage de logarithmes et de la formule 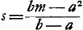 du § 4. du § 4.
|
|



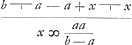 Fiet ut b - a ad a ita a ad
Fiet ut b - a ad a ita a ad