Oeuvres complètes. Tome XX. Musique et mathématique

[p. 265]

VIII. Problema Alhaseni.
[1669. 1670?]

1669

A¹⁾. Dato speculo sphaerico convexo aut cavo, datisque puncto visus et puncto rei visae, invenire in superficie speculi punctum reflexionis.

[Fig. 15]

Ducto plano per speculi centrum A [Fig. 15], et per puncta B, C, oculi et rei visae, fiat sectio in speculi sphaera circulus DP. Junctâque BC sit in eam perpendicularis AE. Et posito puncto reflexionis D, sit etiam DG perpendicularis in BC, et DH perpendicularis in AE. et ducatur recta ADE, quae secabit necessario angulum BDC bifariam, ideoque erit ut BD ad DC ita BF ad FC. quare sumta FQ ∞ FC (quam pono minorem duarum BF, FC) factoque ut BQ ad BF ita FC ad FV, necessario circum-

1) ‘Chartae Mathematicae’ f. 145. Les Fig. 15, 16 et 17 correspondent exactement à des figures des p. 119 et 124 du Manuscrit D qui contient en cet endroit les calculs primitifs, datant apparemment de janvier 1669, puisque la p. 145 porte la date 1 Fevr. 1669. La Fig. 16 correspond aussi à celle de la page, imprimée par Huygens lui-même d'après son procédé spécial, qui est reproduite dans notre T. VI (planche vis-à-vis de la p. 462); le texte de cette page correspond - à quelques variantes près - avec celui de la ‘Constructio’ de la présente Pièce (et aussi avec le texte de la p. 124 du Manuscrit D). La première partie de la présente Pièce motive cette construction ou du moins fournit les données qui permettent de la vérifier.

[p. 266]

ferentia descripta centro V radio VF transibit per punctum D, ut aliunde constat²⁾.

Sint jam AE ∞ a. EB ∞ b. EC ∞ c. radius AD ∞ d. AH ∞ x. HD ∞ y. Ergo FE ∞ ay/x.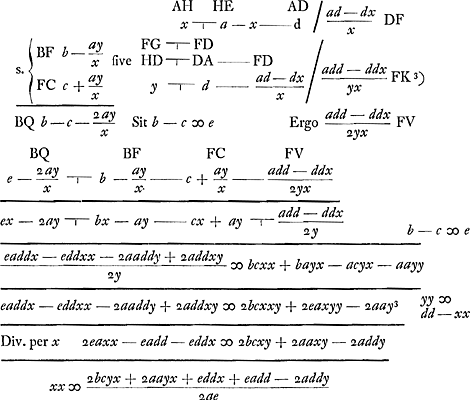

³⁾

Completo igitur rectangulo AHDT, positaque AT ∞ y erit TD ∞ x, punctumque D erit ad hyperbolam ut constat ex aequatione. Sed et ad circumferentiam DP quia

2) Il s'agit, d'après la construction de Huygens, de la circonférence de cercle qui constitue le lieu de tous les points du plan considéré pour lesquels le rapport des distances aux deux points fixes B et C a la valeur constante DB : DC.

3) Puisque l'angle FDK est droit.

[p. 267]

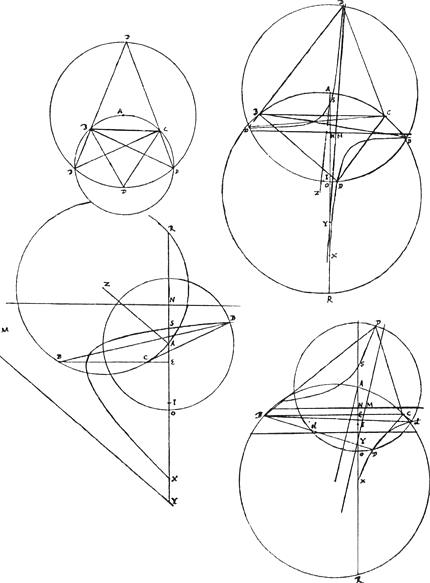
dd - yy ∞ xx. Ergo inventa hyperbola quae locus est puncti D in recta TD, ea circumferentiam DP secabit in puncto D quaesito. Invenietur autem hoc modo.

Constructio⁴⁾.

Per tria puncta A, B, C [Fig. 16] describatur circuli circumferentia cujus centrum sit Z. Occurrat autem ei producta AE in R. Et sit duabus RA, OA tertia proportionalis NA, eritque NM parallela BC, altera asymptotôn. Rursus sint proportionales EA,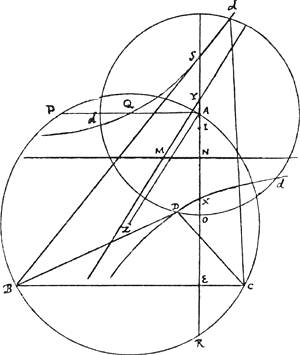

[Fig. 16]

½AO, AI, sumtaque IY ∞ IN, ducatur YM parallela AZ. eaque erit altera asymptotos. Ductâ denique AP in circulo parallelâ BC, divisâque bifariam in Q, erit Q punctum per quod altera oppositarum sectionum transibit⁵⁾. Ad inventas asymptotos describendis⁵⁾, quarum intersectiones cum circumferentia DO, ostendent puncta reflexionis quaesita, quae usque ad quatuor vera esse possunt cum puncta B, C intra circulum Dd data sunt.

Constructio haec ad omnes casus, quibus problema solidum, accommodata est, praeter unum quo non hyperbola sed parabola describenda est, cum nempe circumferentia per puncta A, B, C descripta tangit rectam AE [Fig. 17]⁶⁾. Invenietur

4) Malgré les calculs du Manuscrit D, mentionnés dans la note 1 de la p. 265, il n'est pas clair comment Huygens parvient à cette construction; mais il n'est pas difficile de la vérifier. L'équation de l'hyperbole étant on trouve, en posant y = 0, : c'est l'équation de l'asymptote horizontale.
Comme la circonférence de cercle passant par A, B et C a pour équation , on trouve ; et comme AO = d, on a , conformément à l'équation trouvée de l'asymptote.
Le centre Z de la circonférence a pour coördonnées , ; l'équation de la droite AZ est donc . Or, l'équation de l'hyperbole donne effectivement, en divisant par y² et en posant ensuite y = ∞, ou , de sorte que la deuxième asymptote est parallèle à AZ. Etc.

5) Cette dernière phrase, écrite en marge au crayon, remplace les lignes biffées que voici: denique sumtis IX, IS quae singulae possint ½ qu. AO una cum qu. AI, erunt puncta X et S in hyperbola aut sectionibus oppositis Dd. Ces lignes font encore partie du texte de la planche du T. VI, dont il est question dans la note 1 qui précède.
Dans la Fig. 16 la droite AQP, avec les lettres P et Q, a été ajoutée au crayon.
Le bout de phrase ‘Ad inventas asymptotos describendis’ se rattache aux lignes biffées; le mot ‘describendis’ se rapporte donc à ‘hyperbola aut sectionibus oppocitis Dd’.

5) Cette dernière phrase, écrite en marge au crayon, remplace les lignes biffées que voici: denique sumtis IX, IS quae singulae possint ½ qu. AO una cum qu. AI, erunt puncta X et S in hyperbola aut sectionibus oppositis Dd. Ces lignes font encore partie du texte de la planche du T. VI, dont il est question dans la note 1 qui précède.
Dans la Fig. 16 la droite AQP, avec les lettres P et Q, a été ajoutée au crayon.
Le bout de phrase ‘Ad inventas asymptotos describendis’ se rattache aux lignes biffées; le mot ‘describendis’ se rapporte donc à ‘hyperbola aut sectionibus oppocitis Dd’.

6) Ici finit le texte de la planche du T. VI. Lorsque la circonférence touche la droite AE, on a AR = 0, donc (note 4 de la p. 267), de sorte que l'équation de la conique représente en effet une parabole.

[p. 268]

autem punctum I eodem modo quo prius, per quod ductâ IK parallelâ BC, erit ea axis parabolae. Latus rectum vero tertia proportionalis diametro AL et radio AO,

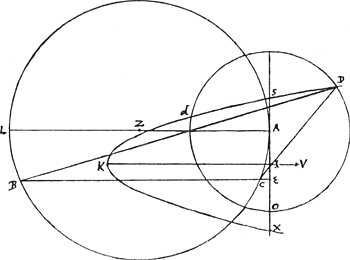[Fig. 17]

quae sit IV. Deinde inventis ut ante punctis S, X, per quae parabola transire debet, facile jam vertex K invenietur, sumta duabus IV, IX tertia proportionali IK.

Notandum est puncta intersectionis circuli et hyperbolae vel parabolae etsi non omnia sint puncta reflexionis, ita tamen sita esse ut angulum à rectis BD, DC comprehensum, vel eum qui deinceps est, recta AD ex centro ducta bifariam secet.

Planum vero erit problema cum vel puncta A, B, C in eadem erunt recta vel cum B et C aequaliter ab A distabunt, quorum prius ex aequatione patet posito nempe a ∞ 0. nam tunc 2bcy ∞ ∓ edd, hoc est y ∞ ∓ edd/2bc. Posterius vero, posito e ∞ 0, tunc enim vel y ∞ 0, vel bcx ∓ aax ∞ add. quo casu intersectio circulorum Dd, ABC duo alia vera reflexionis puncta monstrat si B et C sint intra circulum Dd.

Des quatre figures de la Fig. 18 deux se rapportent à des cas où il y a quatre points de réflexion satisfaisant à la demande, tandis que dans les deux autres il y a respectivement un et trois points de réflexion.

[p. 269]

Ajouté au crayon: multo meliorem constructionem postea invenimus⁷⁾.

[Fig. 18]

7) Il s'agit de la construction du Manuscrit 11 qui constitue notre Appendice II à la p. 330 qui suit. Consultez aussi notre remarque sur cet Appendice à la p. 271 qui suit.

[p. 270]

B⁸⁾. Construction d'un Problème d'Optique, qui est la XXXIX. Proposition du Livre V. d' Alhazen, & la XXII du Livre VI. de Vitellion.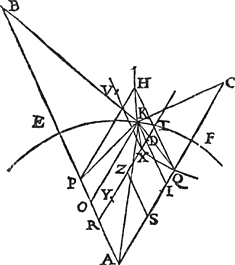

[Fig. 19]
XV aurait dû être une ligne droite.

Les points B C [Fig 19] et le cercle EK dont le centre est A sont donnez sur un mesme plan; il faut trouver le point K sur le cercle, en sorte que les lignes BK, CK fassent avec la ligne AK des angles égaux entr'eux.

Ayant mené AB, AC soit fait comme AC à AF, ainsi AF à AQ; & comme AB à AE, ainsi AE à AP. Soit aussi AR & AS, chacune la moitié de AP & de AQ. Dans l'angle BAC soit achevé les parallélogrammes PAQH & ARZS. Sur RZ prolongée soit pris ZY & ZX, chacune égale à la ligne qui peut la difference d'entre les quarrez de QS & ZS⁹⁾. Ayant fait XV égale à XY et parallèle à AB, sur les deux costez XV, XY soit décrit une hyperbole qui passera par les points Q & H, comme il est évident par la construction: cette hyperbole QXH rencontrera le cercle au point K qui est celuy que l'on cherche.

Ayant mené KO, & KI parallèles à AC & à AB, dont KI rencontre YX au point D; à cause de l'hyperbole le rectangle YDX est égal au quarré de KD ordonnée, ou de OR; & le rectangle YTX est égal au quarré de HT ou de PR; & ayant osté du rectangle YTX le rectangle YDT [lisez: YDX¹⁰⁾], & du quarré de PR le quarré de OR, il restera le rectangle RDT ou AIQ qui sera égal au rectangle AOP: donc PO est à AI ou OK son égale, comme QI est à AO ou IK. Et ayant mené les lignes KP, KQ, les triangles KOP, KIQ seront semblables, & partant équiangles; c'est pourquoy les angles APK, AQK qui sont les mesmes ou les supplemens des angles

8) ‘Divers ouvrages de mathématique et de physique par MM. de l'Académie Royale des Sciences’, 1693, p. 336. Comparez la note 56 de la p. 207 qui précède.

9) C.à.d. Z est le centre de l'hyperbole équilatère, dont l'équation par rapport à deux diamètres conjugués RT et SZ est TZ² - HT² = ZX², ou, si l'on veut, ou bien ou HT² = TY. TX.

10) L'erreur a été corrigée dans la traduction latine des ‘Opera Varia’ de 1724 (tome IV, p. 759).

[p. 271]

égaux OPK, IQK seront égaux entr'eux. Mais par la construction on a fait comme AB à AE ou à AK, ainsi AK ou AE à AP: c'est pourquoy les deux triangles BAK, KAP sont semblables; & pour les mesmes raisons les deux triangles CAK, KAQ sont aussi semblables: c'est pourquoy l'angle BKA est égal à l'angle APK; & l'angle CKA est égal à l'angle AQK. Mais nous venons de démontrer que les angles APK, AQK sont égaux; les angles BKA, CKA seront donc aussi égaux entre eux; ce qu'il fallait démontrer.

Si le point H tomboit sur la circonserence du cercle, ce point H seroit le point K que l'on cherche, & les lignes HP, KP, KO & semblablement les lignes HQ, KQ, KI ne feroient qu'une mesme ligne HP & HQ, d'où l'on prouveroit les mesmes choses qu'on a fait cy-devant, sans avoir besoin de l'hyperbole.

Dans une lettre du 3 septembre 1693 au marquis de l'Hospital (T. X, p. 497) Huygens se dit ‘fachè de voir qu'on ait mis dans les Traitez de l'Academie des Sciences’ la présente solution du problème d'Alhazen, et ‘non pas une beaucoup meilleure’ sur laquelle on peut consulter, outre cette page du T.X., ce que nous observons au début de l'Appendice II à la Pièce VIII à la p. 330 qui suit.

A notre avis Huygens n'avait pas grande raison d'être fâché. L'hyperbole de la Fig. 19 - nous le disons aussi dans la note 2 de la p. 331 qui suit - est la même que celle de la pièce 1891 de 1672 du T. VII et aussi que celle de la solution et de la démonstration de 1673 de l'Appendice II que nous venons de mentionner lesquelles sont appelées par Huygens sa ‘plus belle solution et demonstration’.

On voit dans la Fig. 19, quoiqu'ici cela ne soit pas dit, que pour des raisons de symétrie l'autre branche de l'hyperbole doit passer par le point A, ainsi que par le point P.