Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 260]
| |||||||
VII. Sur la quadrature arithmétique de l'hyperbole par Mercator et sur la méthode qui en résulte pour calculer les logarithmes.
| |||||||
[pagina 261]
| |||||||
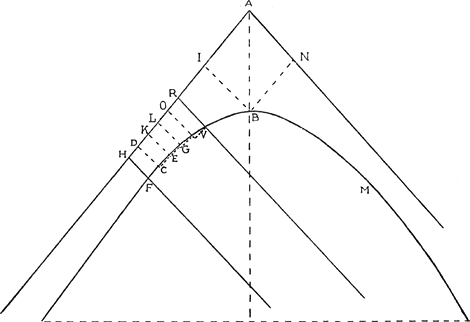
Qu'il y ait maintenant quelque espace hyperbolique FVRH, compris d'une portion de la courbe FV, des deux paralleles a l'asymptote AN, et de la partie qu'elles enferment de l'autre asymptote savoir HR, dont on veüille trouuer le contenu c'est a dire sa proportion au quarré ou rhombe AB; et il n'importe que VR tombe entre BI, FH ou entre BI, NA, quoyque la supputation se fera d'autant plus facilement que HR sera plus petite a raison de HA, comme il paroistra cy apres. La methode pour paruenir a la mesure de l'espace VRHF, consiste premierement a concevoir des petits rectangles ou parallelogrammes circonscrits a tout cet espace comme CH, ED, GK, &c, dont les costez soient paralleles à l'asymptote AN, et leurs largeurs sur l'autre asymptote toutes égales. Et quoyque ces parallelogrammes surpassent de quelque chose l'espace VRHF, toutes fois en considerant comme fait l'auteur qu'il y en a un nombre infini l'on peut dire qu'ils egalent parfaitement ledit espace et il ne reste qu'a trouuer la grandeur de tous ces parallelogrammes mis en une somme. On suppose pour cela AH égale a l'unité ou 1. HR égale a A; IA egale a b. et chasque largeur des petits parallelogrammes comme HD, DK, égale a a. Il est constant maintenant par la proprieté cogneüe de l'hyperbole que comme AH ou 1 est a AI ou b, ainsy AI a FH qui sera bb/1 ou bb. Et par la mesme raison parce que AD est 1 - a, DC sera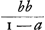 , , 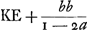 , , 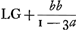 et ainsy des autres hauteurs des petits parallelogrammes.
Mais en faisant la diuision de bb par 1 - a, on trouuera que et ainsy des autres hauteurs des petits parallelogrammes.
Mais en faisant la diuision de bb par 1 - a, on trouuera que 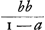 c'est a dire CD est egale à bb + bba + bbaa + bba3 + bba4 &c. a l'infini, c'est a dire à bb multiplié par 1 + a + a2 + a3 + a4 &c. Et partant en multipliant cette hauteur CD par a le parallelogramme CH sera egal à 1 + a + a2 + a3 &c. in abb. De mesme en divisant bb par 1 - 2a on trouvera que c'est a dire CD est egale à bb + bba + bbaa + bba3 + bba4 &c. a l'infini, c'est a dire à bb multiplié par 1 + a + a2 + a3 + a4 &c. Et partant en multipliant cette hauteur CD par a le parallelogramme CH sera egal à 1 + a + a2 + a3 &c. in abb. De mesme en divisant bb par 1 - 2a on trouvera que 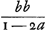 c'est a dire EK est egale a bb in 1 + 2a + c'est a dire EK est egale a bb in 1 + 2a +
| |||||||
[pagina 262]
| |||||||
4aa + 8a3 + 16a4 &c. Et partant le parallelogramme ED sera 1 + 2a + 4aa + 8a3 + 16a4 &c. in abb. Et ainsy en examinant tous les autres petits parallelogrammes on verra facilement qu'ils sont ainsy
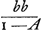 , c'est a dire VR, est egale à cette progression multipliée par bb. Et par conséquent en multipliant de plus par RO ou a le parallelogramme VO doit estre 1 + A + A2 + A3 &c. in abb. , c'est a dire VR, est egale à cette progression multipliée par bb. Et par conséquent en multipliant de plus par RO ou a le parallelogramme VO doit estre 1 + A + A2 + A3 &c. in abb.
Mais pour ce qui est de la consequence par laquelle la somme de tous les parallelogrammes est egalle a A + ½A2 + ⅓A3 &c in bb, elle est fondée sur des Theoremes assez connus des progressions des puissances. Car en considerant les colonnes descendantes des quantites escrites cy dessus on void que la premiere colonne est faite d'unitez multipliées par abb qui font des parallelogrammes egaux entre eulx, dont la somme par consequent sera egalle au dernier abb pris autant de fois qu'il y a des particules egales en la ligne HR ou A faisant les largeurs desdits parallelogrammes. C'est a dire si on met n pour ce nombre infini des parties la somme de tous les parallelogrammes sera nabb, mais na, c'est a dire une des parties multipliée par le nombre des parties est egale a la ligne HR ou A, donc toute la premiere colonne continuée a l'infiny est egale a Abb, comme elle a esté mise. Pareillement la seconde colonne estant a + 2a + 3a + 4a &c. multipliez par abb qui est une suitte de parallelogrammes qui sont comme les nombres depuis l'unité, il est certain que leur somme est egale a la moitié du plus grand A in abb, multipliée par n, c'est a dire prise autant de fois qu'il y a des petites parties en HR ou A. Cette somme sera donc ½ Aanbb, ou parce que na est egale a A ce sera ½ AAbb comme elle a esté mise. De mesme la troisième colonne estant aa + 4aa + 9aa &c. multipliez par abb qui est une suite de parallelogrammes qui sont entre eux comme les quarrez des nombres depuis l'unité: leur somme sera egalle a ⅓ du plus grand multiplié par A c'est a dire a ⅓ AAnabb ou parce que na est egal a A ce sera ⅓ A3bb; et ainsy du reste. Supposant maintenant quelque nombre pour la longueur de A ou HR qui soit moindre que l'unité (car HA est supposé + 1) et de mesme pour b ou AI, la somme susdite A + ½A2 + ⅓A3 + ¼A4 &c. in bb exprimée en nombre sera le contenu de l'espace hyperbolique HFVR. Et quoyqu'il puisse sembler d'abord qu'on cherchera en vain cette somme, parce qu'il y a une multitude infinie de quantitez a adiouter, cependant puifque A est une fraction moindre que l'unité, il s'ensuit que les puis- | |||||||
[pagina 263]
| |||||||
sances de A deviennent d'autant moindres que l'unité qu'elles sont plus hautes, en sorte que les dernieres peuuent estre negligées comme il paroistra par cet exemple. Soit AH ∞ 1; b ∞ 1/10 que l'on escrira ainsy 0, 1; et par conséquent bb ∞ 1/100 ou 0,01; HR ou A ∞ 21/100 ou 0,21.  pour le contenu de l'espaçe hyperbolique FHRV en parties dont le quarré ou Rhombe AB en contient 0,01. Cest a dire que l'espace FHRV sera au quarré ou Rhombe AB comme 23572233/100000000 a 1Ga naar voetnoot4). | |||||||
[pagina 264]
| |||||||
Par la maniere de cette operation il est facile de comprendre la raison de ce qui a esté dict au commencement scavoir que le calcul sera d'autant plus aisé que HR aura moindre raison a HA et d'autant plus long que cette raison sera plus grande, car suiuant cela les puissances de A ou HR diminueront plus ou moins viste pour pouuoir estre negligées ainsy que dans l'exemple proposé l'on voit que les Caractères signifiant des puissances de A se retirent assez viste vers la main droite. Ce qui n'arriveroit pas de mesme si A estoit 0,7 ou 0,8, mais il faudroit continuer l'operation plus auant pour auoir le mesme nombre de veritables caracteres pour le contenu de l'espace hyperbolique. Or cette dimension de l'hyperbole sert aussy a trouver les logarithmes avec facilité parce que ces espaces hyperboliques comme VRHF, BIHF sont tousiours entre eulx comme la raison de VR a FHGa naar voetnoot5) est a la raison de BI a FHGa naar voetnoot5) ce que Gregorius de Sancto Vincentio a monstré le premierGa naar voetnoot5). C'est a dire si l'on pose des nombres pour BI, VR, FH alors comme l'espace VRHF est a BIHF ainsy sera la difference des logarithmes des nombres VR, FH a la difference des logarithmes de BI, FH. La proportion desquelles differences estant connue et supposant ensuitte comme dans les tables 0 pour logarithme de l'unité et 1,0000000000Ga naar voetnoot6) pour celuy de 10, l'on trouue facilement les logarithmes de chaque nombre tels qu'ils sont dans les mesmes tables. |
|