Oeuvres complètes. Tome XX. Musique et mathématique

[p. 256]

IV. De curvis paraboloidibus et hyperboloidibus.
1667¹⁾.

Dans le T. II des Registres le texte de cette Pièce suit celui de la Pièce III.

1) Dans les Registres la Pièce fait corps avec la précédente et n'a donc pas de titre. Dans sa lettre de septembre 1686 à de la Hire - citée aussi dans la note 83 de la p. 212 ainsi que dans la note 125 de la p. 219 qui précèdent - Huygens l'appelle ‘Dimensio Paraboloidum, ou je pourray joindre celle des Hyperboloides’.

Lemma.

Si differentia linearum FL, KL, quae est KF dividatur in quotcunque partes aequales punctis T, S, G, ratio .................................... etc.

C'est à d'insignifiantes différences près (p.e. ‘quotcunque partes’ au lieu de ‘partes quotcunque’), le Lemma qui occupe les p. 283-284 du T. XIV. Ce Lemma nous semble dater de 1667, et non pas de 1657 comme le dit le T. XIV où il est emprunté à une feuille séparée²⁾. En effet, la première rédaction du Lemma - les ratures indiquent que c'est bien la première - se trouve à la p. 188 du Manuscrit C, laquelle date de juillet 1667.

Le Lemma dans la communication est suivi par le

2) Il faut lire à la p. 283, l. 3 du T. XIV ‘Ratio FL ad LK’, non pas ‘ad LT’, et à la p. 284, l. 2 ‘rationem FL’ au lieu de ‘ratione FL’. Nous avons remarqué dans la note 7 de la p. 283 que, par suite d'une inadvertance, Huygens ne s'est pas exprimé correctement. Ceci s'applique au texte de la communication à l'Académie comme à celui du T. XIV.

Theorema.

Si a puncto in paraboloide recta ad axem ordinatim applicetur .... etc., exactement comme dans les feuilles détachées qui ont fourni le texte des p. 284-287 du T. XIV auxquelles nous renvoyons le lecteur. La remarque de Huygens dans la note finale 5 de la p. 287 ‘Convenit .... ad BQ’ fait aussi partie du texte des Registres, et l'on y trouve en cet endroit la ‘figure entièrement analogue à la Fig. 6 de la p. 279’ dont il est question dans la note nommée.

Ce Theorema date apparemment aussi de 1667 puisque dans le Manuscrit C il fait suite au Lemma. Il en est de même du Theorema suivant (p. 285 du T. XIV) qui correspond à celui de la page antérieure 186 du Manuscrit C³⁾. A la p. 185 du Manuscrit C Huygens commençait sa

3) La démonstration n'y est pas achevée et s'arrète au milieu d'une phrase.

[p. 257]

Pièce par les mots: Paraboloides voco curvas in quibus ordinatim applicatae ad axem vel earum potestates quaedam sunt inter se ut interceptae inter easdem applicatas et verticem, vel aliquae earum potestates. Etc.

D'après la note 5 déjà mentionnée de la p. 287 du T. XIV Huygens ajouta encore au crayon à la feuille séparée considérée en cet endroit la remarque Addenda quadratura Hyperboloidum ce qui correspond à ce qu'il a écrit dans la lettre de 1686 citée dans la note 1. Il nous semble que le texte de l'Appendice II (p. 288 et suiv.) du T. XIV, emprunté à la même feuille séparée, doit dater également de 1667 et non pas de 1657: à la p. 190 du Manuscrit C, datant de 1667, on trouve des remarques analogues - quoique non pas identiques - sur les ‘hyperboloides’ ou hyperboles de divers degrés. La publication du texte de cette page du Manuscrit C nous semble superflue.

Outre les parties déjà publiées la communication comprend encore un théorème final que voici. Il correspond en grande partie au texte de la p. 185 du Manuscrit C. Le fait qu'il s'agit ici de la construction d'une tangente d'après la méthode de la Pièce III explique que dans les Registres les Pièces III et VI aient été soudées l'une à l'autre de manière à former en quelque sorte une seule Pièce.

Theorema.

Si Paraboloidem tangens recta linea cum axe conuenit, et a puncto contactus recta ad axem ordinatim applicetur; erit pars axis inter applicatam et tangentem intercepta, ad partem ejusdem axis inter applicatam et verticem, ut exponens potestatis quae in ea paraboloide consideratur in ordinatim applicatis, ad exponentem potestatis quae consideratur in partibus axis, abscissis ad verticem.

Ut si sit Paraboloides AF [Fig. 14] cuius axis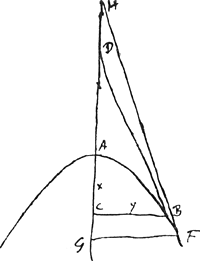

[Fig. 14]

AG vertex A, rectaque eam tangens in puncto B conueniat cum axe in D, sit autem Paraboloides eius naturae ut applicatarum ordinatim BC, FG, quadrato cubi sint inter se sicut quadrata CA, GA, hic quia in ordinatim applicatis consideratur potestas quinta, in abscissis vero ad verticem potestas secunda, dico fore DC ad CA, ut 5 ad 2. Hoc facile ostenditur ex Methodo tangentium. Quod si vero alia item tangens ducatur FH manifestum est ut DA ad AC, et ut AH ad AG, ita esse HD ad CG.