Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 242]
| |
Règle pour trouver les tangentes des lignes courbes.
| |
[pagina 243]
| |
III. Regula ad inveniendas tangentes linearum curvarum.
| |
[pagina 244]
| |
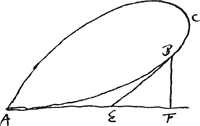
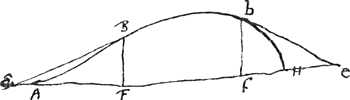
Soit donnée une courbe telle que BC [Fig. 9] ayant une relation connue avec une droite AF donnée également en position. Par
 [Fig. 9.]
conséquent l'ordonnée partant d'un point quelconque B de la courbe est la droite BF la quelle rencontre la droite AF sous un angle donné BFA, et un point A dans la droite AF étant donné, la relation entre AF et FB est exprimée par une certaine équation. Supposons par exemple, en posant AF = x et FB = y, que ce soit l'équation 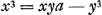 où a désigne une certaine longueur. où a désigne une certaine longueur.
S'il faut mener au point B une tangente BE qui rencontre la droite AF en E et qu'on pose FE = z, la longueur de cette dernière d'après cette règle - la règle de Fermat abrégée - sera tirée uniquement de l'équation donnée. Transportons tous les termes de l'équation donnée dans le premier membre qui devient donc alors égal à zéro. Multiplions d'abord chacun des termes dans lesquels se trouve y par le nombre des dimensions que cette lettre a dans le terme considéré: leur somme sera notre numérateur. Multiplions ensuite de la même manière chaque terme contenant x par le nombre des dimensions de cette dernière et divisions chacun de ces termes par x: la somme obtenue sera notre dénominateur. En formant la fraction de ce dénominateur avec le numérateur trouvé plus haut nous aurons la quantité égale à z ou FE. Quant aux signes + et -, il faut les garder partout comme ils sont. Même si par hasard la quantité du dénominateur ou du numérateur, ou l'une aussi bien que l'autre, est négative, il faut pourtant les considérer comme si elles étaient positives, en observant seulement que lorsque l'une des deux est positive et l'autre négative, FE doit être prise vers le point A; mais qu'elle doit être prise en sens contraire lorsque les deux quantités sont ou bien positives ou bien négatives. Dans le cas de la courbe proposée dont l'équation est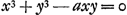 le numérateur deviendra d'après cette règle 3y3 - axy et le dénominateur 3x2 - ay. Partant le numérateur deviendra d'après cette règle 3y3 - axy et le dénominateur 3x2 - ay. Partant 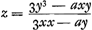 . C'est une longueur connue, x, y et a étant données.
Considérons de même une autre courbe ABH [Fig. 10] à équation . C'est une longueur connue, x, y et a étant données.
Considérons de même une autre courbe ABH [Fig. 10] à équation 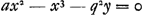 , a et q étant des lignes données, tandis que AF = x et FB = y. Soit BE la tangente et appelons FE z comme auparavant. , a et q étant des lignes données, tandis que AF = x et FB = y. Soit BE la tangente et appelons FE z comme auparavant.
Le numérateur deviendra ici -q2y suivant la règle. Et le dénominateur 2ax-3x2. | |
[pagina 245]
| |
Quod si jam ad punctum B tangens ducenda sit BE, quae occurrat rectae AF in E voceturque FE, z, ejus longitudo per hanc regulamGa naar voetnoot3) inuenietur ex sola aequatione data. Translatis omnibus terminis aequationis datae ad unam aequationis partem, qui proinde aequales fiunt nihiloGa naar voetnoot4); multiplicentur primo termini singuli in quibus reperitur y, per numerum dimensionum quas in ipsis habet y, atque ea erit quantitas dividenda. Deinde similiter termini singuli in quibus x, multiplicentur per numerum dimensionum quas in ipsis habet x, et è singulis una x tollatur; atque haec quantitas pro divisore erit, subscribenda quantitati dividendae jam inuentae, quo facto habebitur quantitas aequalis z siue FE. Signa autem + & - eadem ubique retinenda sunt, atque etiamsi forte quantitas divisoris, vel dividenda, vel utraque minor nihilo siue negata sit, tamen tanquam adsirmatae sunt considerandae: hoc tantum observando, ut cum altera adfirmata est, altera negata, tunc FE sumatur versus punctum A; cum vero utraque vel adfirmata est, vel negata, ut tunc sumatur FE in partem contrariam. In curua proposita cuius aequatio x3 + y - axy3 ∞ 0 fiet secundum hanc regulam dividenda quantitas 3y3 - axy; divisor vero 3xx - ay ideoque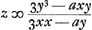 quae est longitudo cognita, cum dentur x, y et a.
Esto item alia curua ABH [Fig. 10], cujus aequatio axx - x3 - qqy ∞ 0 posito scilicet a et q esse lineas datas, AF vero ∞ x, FB ∞ y. Sit BE tangens et FE dicatur quae est longitudo cognita, cum dentur x, y et a.
Esto item alia curua ABH [Fig. 10], cujus aequatio axx - x3 - qqy ∞ 0 posito scilicet a et q esse lineas datas, AF vero ∞ x, FB ∞ y. Sit BE tangens et FE dicatur
 [Fig. 10]
ut ante z. Hic fiet, secundum regulam, dividenda quantitas - qqy. Divisor autem | |
[pagina 246]
| |
D'où 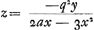 . Or, comme le numérateur est négatif, il faudra, lorsqu'il en est de même du dénominateur, c.à.d. lorsque 2a < 3x, prendre z ou FE du côté opposé à celui où se trouve A; mais lorsque 2a > 3x, il faudra prendre FE du côté de A suivant le précepte de la règle. . Or, comme le numérateur est négatif, il faudra, lorsqu'il en est de même du dénominateur, c.à.d. lorsque 2a < 3x, prendre z ou FE du côté opposé à celui où se trouve A; mais lorsque 2a > 3x, il faudra prendre FE du côté de A suivant le précepte de la règle.
Pour expliquer la raison en même temps que l'origine de la règle simplifiée par 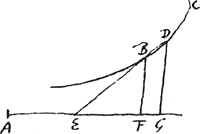 [Fig. 11]
nous, considérons de nouveau une courbe BC [Fig. 11] à laquelle on demande de mener une tangente au point B. Prenons d'abord une droite EBD qui ne touche pas la courbe en B mais qui la coupe tant en ce point qu'en un autre D fort proche de B. Puisse cette sécante rencontrer la droite AG en E, et menons des deux points B, D à la droite AG les deux ordonnées inclinées sous le même angle BF et DG. Soit AF = x et FB = y comme auparavant. Supposons en outre que FG soit une longueur donnée e et cherchons FE = z. On a donc EF : FB, c.à.d. z : y = EG (ou z + e): GD, d'où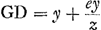 . Il est évident que ceci est vrai pour une courbe quelconque.
Considérons maintenant l'équation exprimant la nature de la courbe; que ce soit par exemple celle proposée plus haut . Il est évident que ceci est vrai pour une courbe quelconque.
Considérons maintenant l'équation exprimant la nature de la courbe; que ce soit par exemple celle proposée plus haut 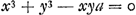 , dans laquelle a désignait une longueur connue (AH). Or, il est évident que lorsque le point D est situé sur la courbe, les deux longueurs AG et GD, c.à.d. x + e et y + ey/z, doivent avoir entr'elles la même relation que AF et FB, c.à.d. x et y. En d'autres termes, lorsque dans l'équation proposée on substitue partout x + e à x et y + ey/z à y, l'équation résultante aura de nouveau zéro dans le second membre. On aura donc , dans laquelle a désignait une longueur connue (AH). Or, il est évident que lorsque le point D est situé sur la courbe, les deux longueurs AG et GD, c.à.d. x + e et y + ey/z, doivent avoir entr'elles la même relation que AF et FB, c.à.d. x et y. En d'autres termes, lorsque dans l'équation proposée on substitue partout x + e à x et y + ey/z à y, l'équation résultante aura de nouveau zéro dans le second membre. On aura donc
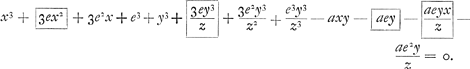 Il est certain que cette équation doit contenir les termes de l'équation précédente qui a servi à sa formation, savoir x3 + y3 - axy. Et comme l'ensemble de ces termes est nul d'après la propriété de la courbe, il est par conséquent nécessaire que, ces termes ayant été supprimés, le reste aussi soit égal à zéro. Or, il est manifeste que dans tous les termes qui sont restés on trouve une ou plusieurs lettres e, et que par conséquent ils peuvent tous être divisés par cette longueur; et je sais qu'il faut égaler à zéro, en | |
[pagina 247]
| |
2ax - 3xx, unde 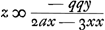 , ubi cum dividenda quantitas sit negata, si fuerit etiam divisor minor nihilo, hoc est si 2a minor quam 3x; erit z siue FE sumenda in partem ab A aversam, si vero 2a major quam 3x sumenda erit FE versus A ex praecepto regulae. , ubi cum dividenda quantitas sit negata, si fuerit etiam divisor minor nihilo, hoc est si 2a minor quam 3x; erit z siue FE sumenda in partem ab A aversam, si vero 2a major quam 3x sumenda erit FE versus A ex praecepto regulae.
Horum vero rationem, ipsiusque regulaeGa naar voetnoot5) originem ut explicemus, proponatur ut ante curua BC [Fig. 11] ad cuius punctum B tangens ducenda sit. Intelligatur primum recta EBD, quae non tangat curuam in B sed eam secet, atque item in alio puncto D, ipsi B proximo. rectae autem AG occurrat in E et ab utrisque punctis B, D, ducantur ad rectam AG, ijsdem angulis inclinatae, BF, DG, et sit AF ∞ x, FB ∞ y sicut antea; ponatur etiam FG data esse quae sit e quaeraturque FE ∞ z. Est itaque sicut EF ad FB, hoc est sicut z ad y; ita EG, hoc est z + e ad GD quae erit y + ey/z, et hoc quidem in qualibet curua ita se habere manifestum est. Nunc porro consideretur aequatio naturam curuae continens, exempli gratia illa superius proposita x3 + y3 - xya ∞ 0, ubi a rectam longitudine datam, velut AH significabat. Et patet cum punctum D in curua ponatur debere eodem modo duas AG, GD, hoc est x + e et y + ey/z ad se mutuo referri atque AF, FB, hoc est x et y. Nempe si in aequatione proposita pro x substituatur ubique x + e et pro y, ubique y + ey/z, debebit aequatio hinc formata terminos omnes habere aequales nihilo, hoc est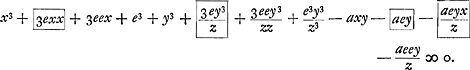 In hac autem aequatione constat necessario terminos prioris aequationis ex qua formata est contineri debere, nempe x3 + y3 - axy, qui cum sint aequales nihilo ex proprietate curuae, idcirco his in aequatione deletis, necesse est etiam reliquos aequari nihilo. In quibus singulis manifestum quoque est vel unum e vel plura reperiri; ideoque omnes per e dividi posse. qui autem post hanc divisionem non amplius habebunt e, eos, neglectis reliquis, scio nihilo aequari debere, quantitatemque lineae z siue FE ostensuros; si nempe BE tanquam tangens consideretur, ideoque FG seu e infinite parua. | |
[pagina 248]
| |
négligeant les autres, tous ceux qui, après cette division, ne contiendront plus e. L'équation ainsi obtenue donnera la droite z ou FE, bien entendu dans le cas où BE est considérée comme une tangente de sorte que FE ou e est infiniment petite. Car les termes dans lesquels e est restée représenteront alors des quantités infiniment petites ou entièrement évanouissantes.
Jusqu'ici nous avons expliqué l'origine et la raison de la règle de Fermat. Voyons maintenant de quelle manière elle a été amenée à une si grande concision. Je constate que de la dernière équation écrite plus haut il suffit de conserver les termes qui contiennent e une seule fois. On a donc ici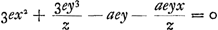 . Il s'agit d'expliquer comment ces termes se déduisent avec facilité de ceux de l'équation donnée . Il s'agit d'expliquer comment ces termes se déduisent avec facilité de ceux de l'équation donnée 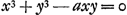 . Il apparaît d'abord que 3ex2 et 3ey3/z ne sont rien d'autre que les deuxièmes termes des cubes de x + e et de y + ey/z et qu'ils se trouvent ici parce que dans l'équation donnée il y avait x3 et y3. Quant à tous les autres termes de ces cubes, de même que les termes correspondants d'autres puissances quelonques de x + e et de y + ey/z, ils contiennent e soit plusieurs fois soit point du tout; comme nous l'avons déjà dit, on les écrirait donc inutilement. Par conséquent, s'il y avait d'autres puissances de x et de y dans l'équation proposée, il faudrait écrire dans la séconde équation seulement les deuxièmes termes des mêmes puissances de x + e et de y + ey/z, en remarquant que ces deuxièmes termes se déduisent des puissances données de x et de y d'après une méthode fixe, savoir, pour une puissance quelconque de
x, en changeant une lettre x en e et en ajoutant un facteur numérique égal au nombre des dimensions de x. De cette façon on trouve ici 3ex2. D'autre part chaque puissance d'y doit être multipliée par e/z, le facteur numérique égal au nombre des dimensions y étant de plus ajouté. Ainsi notre terme y3 donne 3y3e/z. La raison ressort immédiatement du mode de formation des puissances. . Il apparaît d'abord que 3ex2 et 3ey3/z ne sont rien d'autre que les deuxièmes termes des cubes de x + e et de y + ey/z et qu'ils se trouvent ici parce que dans l'équation donnée il y avait x3 et y3. Quant à tous les autres termes de ces cubes, de même que les termes correspondants d'autres puissances quelonques de x + e et de y + ey/z, ils contiennent e soit plusieurs fois soit point du tout; comme nous l'avons déjà dit, on les écrirait donc inutilement. Par conséquent, s'il y avait d'autres puissances de x et de y dans l'équation proposée, il faudrait écrire dans la séconde équation seulement les deuxièmes termes des mêmes puissances de x + e et de y + ey/z, en remarquant que ces deuxièmes termes se déduisent des puissances données de x et de y d'après une méthode fixe, savoir, pour une puissance quelconque de
x, en changeant une lettre x en e et en ajoutant un facteur numérique égal au nombre des dimensions de x. De cette façon on trouve ici 3ex2. D'autre part chaque puissance d'y doit être multipliée par e/z, le facteur numérique égal au nombre des dimensions y étant de plus ajouté. Ainsi notre terme y3 donne 3y3e/z. La raison ressort immédiatement du mode de formation des puissances.
Il apparaît en outre facilement ce qu'il faut écrire dans la seconde équation à cause de la présence de xy dans le terme - axy de l'équation donnée. En esset, comme il faut substituer à xy le produit de x + e par y + ey/z en écrivant seulement les termes qui contiennent e une seule fois, nous ne multiplions par y que le second des termes x et e, et par x seulement le second des termes y et ey/z. Nous obtiendrons ainsi ey + | |
[pagina 249]
| |
Nam termini in quibus adhuc e superest etiam quantitates infinite paruas siue omnino euanescentes continebuntGa naar voetnoot6). Video itaque ex aequationeGa naar voetnoot7) tantum eos terminos scribi necesse esse quibus inest e simplex, velut hic 3exx + 3ey3/z - aey - aeyx/z ∞ 0, qui termini quomodo facili negotio ex datis aequationis terminis x3 + y3 - axy ∞ 0 describi possint deinceps explicandum. Et primo quidem apparet 3exx + 3ey3/z nihil aliud esse quam secundos terminos cuborum ab x + e et ab y + ey/z ideo scriptos, quia in aequatione habentur cubi ab x et y, nam reliqui omnes termini cuborum, ut et quarumuis aliarum potestatum ab x + e et ab y + ey/z, vel plura quam unum e habent, vel nullum; ideoque uti jam diximus frustra scriberentur. Eadem itaque ratione, si aliae potestates ab x vel y essent in aequatione propositae [lisez plutôt: propositaGa naar voetnoot8)], scribendi forent in aequatione altera, termini secundi tantum similium potestatum ab x + e et ab y + ey/z notandumque secundos hosce termines ex ipsis datis potestatibus ab x et y certa ratione confici, nempe ex potestate quauis x, velut x3, mutando unum x in e et praeponendo numerum dimensionum ipsius x. Ita hic fit 3exx. Ex potestate y vero ducendo eam in e/z praeponendoque similiter numerum dimensionum ipsius y. Ita hic ab y3 fit 3y3e/z quorum quidem rationem ex potestatum formatione intelligere facillimum. Porro propter xy in termino aequationis - axy, facile quoque apparet quid in aequatione secunda scribendum sit. cum enim substituendum fit pro xy productum ab x + e in y + ey/z, sed ea tantum scribenda in quibus unum e, ideo de duobus x + e tantum e ducemus in y et tantum x in ey/z adeoque fient ey + exy/z quibus in a ductis, praepositoque signo -, quia habetur - axy, existet - aey - aexy/z sicut supra. | |
[pagina 250]
| |
exy/z et en les multipliant par - a, puisqu'il y avait - axy, il viendra - aey - aexy/z comme ci-dessus. De la même manière, sil y avait x2y3 dans l'équation proposée, je prendrais à cause de x2 les deux premiers termes du carré de x + e, savoir x2 + 2ex; et à cause de y3 les deux premiers termes du cube de y + ey/z, savoir y3 + 3ey3/z; leur produit doit être substitué à x2y3. Mais ici aussi il suffit de multiplier seulement le premier des deux termes x2 et 2ex par 3ey3/z, et le deuxième seulement par y3, car les autres produits partiels contiendraient e plufieurs fois ou pas du tout. Il vient donc 3ex2y3/z + 2exy3. Il appert par ces considérations que l'un et l'autre des deux termes requis peut toujours être déduit du terme donné, qui est ici x2y3; savoir l'un en changeant une lettre x en e et en y ajoutant comme facteur numérique le nombre des dimensions de x; c'est ainsi en effet qu'on trouve 2aexy3; l'autre en multipliant le terme donné par e/z et en y ajoutant de même comme facteur le nombre des dimensions d'y; c'est ainsi qu on obtient le terme 3ex2y3/z. Or, comme il a été montré un peu plus haut que les termes de la seconde équation proviennent des deuxièmes termes des puissances de x + e et de y + ey/z correspondant aux puissances de x et de y dans l'équation donnée, il est à présent manifeste que les différents termes de l'équation donnée contenant x ou une de ses puissances, donnent lieu dans la seconde équation à un nombre égal de termes ne contenant pas z, tandis que les différents termes contenant y ou une de ses puissances engendrent de la manière susdite un nombre égal de termes fractionnaires ayant z pour dénominateur, sans que cette lettre apparaisse ailleurs. Ceci étant connu, c.à.d. sachant comment de l'équation quelconque proposée, comme ici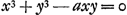 , on en tire une autre, comme ici , on en tire une autre, comme ici 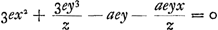 , j'observe ensuite que lorsque les termes ayant z pour dénominateur sont transportés dans l'autre membre et que tous les termes sont multipliés par z, et qu'on divise ensuite par la somme des termes qui primitivement ne contenaient pas cette lettre, on trouve la quantité z toute seule d'un côté de l'équation. De cette façon on obtient ici , j'observe ensuite que lorsque les termes ayant z pour dénominateur sont transportés dans l'autre membre et que tous les termes sont multipliés par z, et qu'on divise ensuite par la somme des termes qui primitivement ne contenaient pas cette lettre, on trouve la quantité z toute seule d'un côté de l'équation. De cette façon on obtient ici 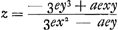 . J'en conclus que pour calculer la quantité z il suffit d'écrire les termes de la seconde équation qui proviennent de ceux des termes de la première qui contiennent y, en supprimant le dénominateur z et en invertissant les signes + et -, et de diviser ensuite ces termes par ceux provenant des . J'en conclus que pour calculer la quantité z il suffit d'écrire les termes de la seconde équation qui proviennent de ceux des termes de la première qui contiennent y, en supprimant le dénominateur z et en invertissant les signes + et -, et de diviser ensuite ces termes par ceux provenant des
| |
[pagina 251]
| |
Sic quoque si in aequatione proposita haberetur xxy3 sumerem propter xx duos priores termines quadrati ab x + e, nempe xx + 2ex; et propter y3 duos priores terminos cubi ab y + ey/z nempe y3 + 3ey3/z quorum productum pro xxy3 surrogandum. sed etiam hic de duobus xx + 2ex tantum xx ducendum in 3ey3/z tantumque 2ex in y3 (nam caetera vel plura quam unum e vel nullum haberent) adeo ut fiat 3exxy3/z + 2exy3. Atque ex his animadvertere licet, semper utrumque eorum terminorum describi posse ex dato termino, qui hic xxy3, alterum quidem mutato uno x in e et praeponendo numerum dimensionum ipsius x: ita enim fit 2exy3: alterum vero ducendo datum terminum in e/z, praeponendoque similiter numerum dimensionum ipsius y; ita enim fit 3exxy2/z. cumque hac eadem immutatione, paulo ante etiam secundos terminos potestatum ab x + e et ab y + ey/z ex potestatibus x et y aequationis datae describi ostensum sit, manifestum jam est a singulis terminis aequationis datae, in quibus x vel potestas eius, describi praedicta methodo, in secunda aequatione, totidem terminos in quibus non est z, a singulis vero in quibus y vel potestas eius, describi totidem terminos, dicta etiam methodo, quarum fractionis denominator sit z, nec alibi hanc litteram in secunda aequatione repertum iri. Hoc igitur cognito quo pacto ex aequatione quauis propofita, velut hic x3 + y3 - axy ∞ 0 alia describenda fit, ut hic 3exx + 3ey3/z - aey - aeyx/z ∞ 0, animadverto porro si termini divisi per z, ad alteram partem aequationis transferantur, ductisque omnibus in z, divisio deinde fiat per terminos in quibus initio non erat z, existere tunc ipsam quantitatem z ab una aequationis parte, uti hic fiet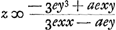 . Atque hinc intelligo ad consequendam quantitatem z ponendos tantum eos terminos aequationis qui descripti sunt ex terminis aequationis primae in quibus y, sublato tantum denominatore z mutatisque signis + & -. deinde dividendes istos terminos per eos . Atque hinc intelligo ad consequendam quantitatem z ponendos tantum eos terminos aequationis qui descripti sunt ex terminis aequationis primae in quibus y, sublato tantum denominatore z mutatisque signis + & -. deinde dividendes istos terminos per eos
| |
[pagina 252]
| |
termes contenant x de la première équation. il paraît en outre que tous les termes tant du numérateur que du dénominateur peuvent être divisés par e; de sorte que dans notre exemple on trouve 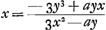 . On supprime donc e/z dans les termes provenant de ceux qui contiennent y. En effet, nous avons dit plus haut qu'ils se dérivaient des termes donnés en multipliant ceux-ci par e/z et en y ajoutant le facteur numérique indiquant les dimensions d'y. On voit donc que pour obtenir ces termes nécessaires pour la détermination de z il n'y a d'autre changement à apporter aux termes contenant y de l'équation donnée, que celui d'y ajouter comme facteur le nombre des dimensions d'y et d'intervertir les signes + et -. De cette façon y3 - axy donne - 3y3 + axy. Quant aux termes provenant de ceux de la première équation qui renferment x, comme il s'est montré qu'il faut seulement y supprimer la lettre e, et comme nous avons dit antérieurement qu'ils sont déduits de telle manière qu'une lettre x a été changée en e et que de plus on y a ajouté comme facteur le nombre des dimensions de x, il appert que désormais, pour constituer le dénominateur requis, il suffit d'ajouter commefacteur à chacun des termes contenant x de la première équation le nombre
indiquant les dimensions de x, et de supprimer ensuite une seule lettre x dans chaque terme. C'est ainsi que de x3 - axy proviendra 3x3 - axy et ensuite, en divisant par x, 3x2 - ay. Par ces raisonnements la règle énoncée au début est maintenant démontrée. Il est vrai que nous avons dit à présent qu'il faut changer les signes + et - dans les termes qui proviennent de ceux contenant y, tandis que dans la règle nous disions qu'il ne faut rien changer dans les signes, mais il est évident que ceci revient au même puisque nous disions aussi qu'il faut considérer chaque quantité négative [numérateur ou dénominateur] comme si elle était positive. Mais pour qu'on comprenne la raison de la remarque ajoutée à la règle sur le sens de la ligne FE, nous répéterons ici la figure considérée plus haut dans laquelle nous avons vu que . On supprime donc e/z dans les termes provenant de ceux qui contiennent y. En effet, nous avons dit plus haut qu'ils se dérivaient des termes donnés en multipliant ceux-ci par e/z et en y ajoutant le facteur numérique indiquant les dimensions d'y. On voit donc que pour obtenir ces termes nécessaires pour la détermination de z il n'y a d'autre changement à apporter aux termes contenant y de l'équation donnée, que celui d'y ajouter comme facteur le nombre des dimensions d'y et d'intervertir les signes + et -. De cette façon y3 - axy donne - 3y3 + axy. Quant aux termes provenant de ceux de la première équation qui renferment x, comme il s'est montré qu'il faut seulement y supprimer la lettre e, et comme nous avons dit antérieurement qu'ils sont déduits de telle manière qu'une lettre x a été changée en e et que de plus on y a ajouté comme facteur le nombre des dimensions de x, il appert que désormais, pour constituer le dénominateur requis, il suffit d'ajouter commefacteur à chacun des termes contenant x de la première équation le nombre
indiquant les dimensions de x, et de supprimer ensuite une seule lettre x dans chaque terme. C'est ainsi que de x3 - axy proviendra 3x3 - axy et ensuite, en divisant par x, 3x2 - ay. Par ces raisonnements la règle énoncée au début est maintenant démontrée. Il est vrai que nous avons dit à présent qu'il faut changer les signes + et - dans les termes qui proviennent de ceux contenant y, tandis que dans la règle nous disions qu'il ne faut rien changer dans les signes, mais il est évident que ceci revient au même puisque nous disions aussi qu'il faut considérer chaque quantité négative [numérateur ou dénominateur] comme si elle était positive. Mais pour qu'on comprenne la raison de la remarque ajoutée à la règle sur le sens de la ligne FE, nous répéterons ici la figure considérée plus haut dans laquelle nous avons vu que 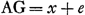 et et 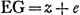 , d'où se concluait , d'où se concluait 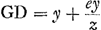 . Si toutefois la tangente tombe de l'autre côté de la ligne BF [Fig. 12], comme ici be, et qu'elle est d'abord, comme l'autre, censée couper la courbe, savoir en d, et qu'on tire dg parallèle à bf, il arrivera qu'en posant de nouveau fg = e et fe = z, Ag devient égale x + e, mais eg à z - e, d'où résulte . Si toutefois la tangente tombe de l'autre côté de la ligne BF [Fig. 12], comme ici be, et qu'elle est d'abord, comme l'autre, censée couper la courbe, savoir en d, et qu'on tire dg parallèle à bf, il arrivera qu'en posant de nouveau fg = e et fe = z, Ag devient égale x + e, mais eg à z - e, d'où résulte
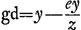 . Il est facile d'en conclure que la seconde équation résultant de l'équation
proposée . Il est facile d'en conclure que la seconde équation résultant de l'équation
proposée 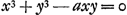 sera dans ce cas sera dans ce cas 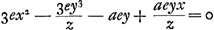 . C.à.d. les termes à dénominateur z y ont des signes contraires à ceux qu'ils avaient dans l'équation antérieurement déduite qui était . C.à.d. les termes à dénominateur z y ont des signes contraires à ceux qu'ils avaient dans l'équation antérieurement déduite qui était 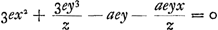 . Il résulte de cette dernière que lorsque la quantité 3ex2 - aey ou plutôt 3x2 - ay (qui constitue le dénominateur suivant la règle) est inférieure à zéro ou négative, . Il résulte de cette dernière que lorsque la quantité 3ex2 - aey ou plutôt 3x2 - ay (qui constitue le dénominateur suivant la règle) est inférieure à zéro ou négative,
| |
[pagina 253]
| |
qui descripti sunt ex terminis aequationis primae, in quibus x. Porro ex omnibus tam divisis quam dividentibus, patet rejici posse e; adeo ut in hoc exemplo fiat 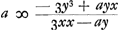 . Itaque rejicitur e/z ex terminis qui descripti sunt ab ijs qui habent y. Sic autem descriptos eos superius diximus, ut ducerentur in idem e/z, praeponereturque numerus dimensionum y. Itaque nihil requiri apparet ad terminos hosce (quatenus ad definiendam quantitatem z hic adhibentur) ex terminis aequationis primae in quibus y describendos, quam ut praeponamus tantum ijs numerum dimensionum quas in ipsis habet y, signaque + & - invertamus, sic nempe ab y3 - axy, describetur - 3y3 + axy. A terminis vero qui descripti sunt a terminis aequationis primae in quibus x, cum tantum e, hic rejiciendum patuerit; cumque eos ita prius descriptos dixerimus, ut unum x mutaretur in e, praeponereturque numerus dimensionum ipsius x; apparet eos quatenus hic adhibentur ad constituendum divisorem, sic tantum describi opus esse ex terminis propositae aequationis in quibus x, ut praeponatur ijs numerus dimensionum ipsius x, ac deinde unum x auferatur; sic nempe ab x3 - axy describetur 3x3 - axy & dempto ubique x uno fiet 3xx - ay; atque ex his ratio regulae ab initio positae manifesta est. nam quod signa + & - in terminis qui
describuntur ab ijs in quibus y, hic immutanda diximus, in regula vero nulla omnino immutanda, id eodem redire liquet, cum quantitatem negatam siue minorem nihilo, tanquam affirmatam considerandam ibi dixerimus. Ut autem ratio . Itaque rejicitur e/z ex terminis qui descripti sunt ab ijs qui habent y. Sic autem descriptos eos superius diximus, ut ducerentur in idem e/z, praeponereturque numerus dimensionum y. Itaque nihil requiri apparet ad terminos hosce (quatenus ad definiendam quantitatem z hic adhibentur) ex terminis aequationis primae in quibus y describendos, quam ut praeponamus tantum ijs numerum dimensionum quas in ipsis habet y, signaque + & - invertamus, sic nempe ab y3 - axy, describetur - 3y3 + axy. A terminis vero qui descripti sunt a terminis aequationis primae in quibus x, cum tantum e, hic rejiciendum patuerit; cumque eos ita prius descriptos dixerimus, ut unum x mutaretur in e, praeponereturque numerus dimensionum ipsius x; apparet eos quatenus hic adhibentur ad constituendum divisorem, sic tantum describi opus esse ex terminis propositae aequationis in quibus x, ut praeponatur ijs numerus dimensionum ipsius x, ac deinde unum x auferatur; sic nempe ab x3 - axy describetur 3x3 - axy & dempto ubique x uno fiet 3xx - ay; atque ex his ratio regulae ab initio positae manifesta est. nam quod signa + & - in terminis qui
describuntur ab ijs in quibus y, hic immutanda diximus, in regula vero nulla omnino immutanda, id eodem redire liquet, cum quantitatem negatam siue minorem nihilo, tanquam affirmatam considerandam ibi dixerimus. Ut autem ratio
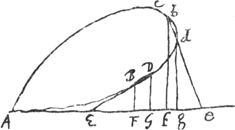 [Fig. 12]
observationis ibidem adjectae, in utram partem linea FE accipienda sit intelligatur, repetemus figuram in principio positam ubi vidimus AG esse x + e. EG vero z + e, unde fiebat 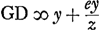 . Si autem [Fig. 12] tangens ab altera parte lineae BF cadere intelligatur, velut be, atque haec primum curuam secare fingatur, ut ibi factum est in d, ducaturque dg parallela bf, fiet ponendo rursus fg ∞ e, et fe ∞ z, ut Ag quidem fiat x + e, sed eg erit z - e, unde . Si autem [Fig. 12] tangens ab altera parte lineae BF cadere intelligatur, velut be, atque haec primum curuam secare fingatur, ut ibi factum est in d, ducaturque dg parallela bf, fiet ponendo rursus fg ∞ e, et fe ∞ z, ut Ag quidem fiat x + e, sed eg erit z - e, unde 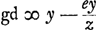 . atque hinc porro facile est perspicere, aequationem secundam quae ex proposita aequatione x3 + y3 - axy ∞ 0 describitur, hoc casu fore . atque hinc porro facile est perspicere, aequationem secundam quae ex proposita aequatione x3 + y3 - axy ∞ 0 describitur, hoc casu fore 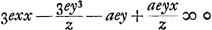 . ut nempe termini qui per z dividuntur, habeant signa contraria ijs quae habebant in aequatione descripta casu priori, quae erat . ut nempe termini qui per z dividuntur, habeant signa contraria ijs quae habebant in aequatione descripta casu priori, quae erat 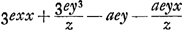 . Ex hac veroGa naar voetnoot9) sequitur, . Ex hac veroGa naar voetnoot9) sequitur,
| |
[pagina 254]
| |
la quantité restante 3ey3/z - aeyx/z, ou aussi la quantité 3y3 - ayx (qui, suivant la règle, constitue le numérateur) est positive; que lorsqu'au contraire celle-là est positive, celle-ci est négative, puisque la somme totale de tous les termes est nulle. Mais il en est autrement dans le cas de l'équation 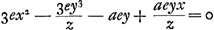 . De celle-ci il résulte que lorsque la quantité 3ex2 - aey, ou plutôt 3x2 - ay, est négative, la partie restante . De celle-ci il résulte que lorsque la quantité 3ex2 - aey, ou plutôt 3x2 - ay, est négative, la partie restante 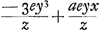 ou aussi la quantité - 3y3 + ayx, est positive, et par conséquent 3y3 - ayx négative; tandis que, lorsque 3x2 - ay est une quantité positive, - 3y3 + ayx doit être négative, et par conséquent l'expression 3y3 - ayx positive.
Ceci fait voir que des quantités trouvées par la règle et contenues dans l'équation ou aussi la quantité - 3y3 + ayx, est positive, et par conséquent 3y3 - ayx négative; tandis que, lorsque 3x2 - ay est une quantité positive, - 3y3 + ayx doit être négative, et par conséquent l'expression 3y3 - ayx positive.
Ceci fait voir que des quantités trouvées par la règle et contenues dans l'équation 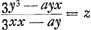 , on peut inférer auquel des deux cas appartient la construction de la tangente: d'une différence de signe entre le dénominateur et le numérateur on peut conclure qu'on se trouve dans le premier cas, c.à.d. que z ou FE doit être prise vers A, tandis que dans le cas de l'égalité des signes c'est dans la direction opposée qu'il faut la prendre.
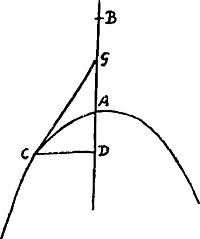
Or, la quantité z ou FE trouvée d'après la règle peut parfois être réduite à des termes plus simples au moyen de l'équation donnée exprimant la nature de la courbe. Il en est ainsi par exemple dans la présente courbe AC [Fig. 13] possédant l'axe AD et le sommet A et dont la nature est telle que si de son point C on mène l'ordonnée CD le produit de BD3 (B étant un point donné sur l'axe en dehors de la courbe) par DA2 est égal à DC5. En d'autres termes posant BA = a, BD = x, DC = y l'équation exprimant la nature de la courbe deviendra , on peut inférer auquel des deux cas appartient la construction de la tangente: d'une différence de signe entre le dénominateur et le numérateur on peut conclure qu'on se trouve dans le premier cas, c.à.d. que z ou FE doit être prise vers A, tandis que dans le cas de l'égalité des signes c'est dans la direction opposée qu'il faut la prendre.
Or, la quantité z ou FE trouvée d'après la règle peut parfois être réduite à des termes plus simples au moyen de l'équation donnée exprimant la nature de la courbe. Il en est ainsi par exemple dans la présente courbe AC [Fig. 13] possédant l'axe AD et le sommet A et dont la nature est telle que si de son point C on mène l'ordonnée CD le produit de BD3 (B étant un point donné sur l'axe en dehors de la courbe) par DA2 est égal à DC5. En d'autres termes posant BA = a, BD = x, DC = y l'équation exprimant la nature de la courbe deviendra 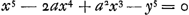 , CG étant une tangente qui rencontre l'axe en G, et posant DG = z, on obtient d'après la règle , CG étant une tangente qui rencontre l'axe en G, et posant DG = z, on obtient d'après la règle 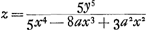 . Mais comme d'après l'équation donnée . Mais comme d'après l'équation donnée 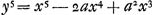 , on trouve, en substituant à 5y5 sa valeur, , on trouve, en substituant à 5y5 sa valeur,
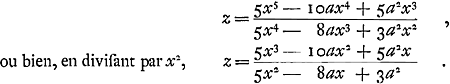 Et en divisant de nouveau par x - a on aura 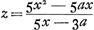 , ce quisignifie que loriqu'on prend le rapport BD : DG égal à 5BD - 3BA (ou 2BA + 5AD): 5AD, GC touchera la courbe AC en C. , ce quisignifie que loriqu'on prend le rapport BD : DG égal à 5BD - 3BA (ou 2BA + 5AD): 5AD, GC touchera la courbe AC en C.
| |
[pagina 255]
| |
quando quantitas 3exx - aey siue quando 3xx - ay (quae divisorem constituit secundum regulam) fuerit minor nihilo, siue negata, tunc quantitatem reliquam 3ey3/z - aeyx/z fiue etiam 3y3 - ayx (quae quantitatem dividendam secundum regulam constituit) esse affirmatam; aut cum illa est affirmata, hanc esse negatam; quia omnes simul aequationis termini aequantur nihilo. At contra ex illa aequatione 3exx - 3ey3/z - aey + aeyx/z ∞ 0 sequitur quando quantitas 3exx - aey, siue 3xx - ay, fuerit negata tunc reliquam - 3ey3/z + aeyx/z, siue etiam - 3y3 + ayx esse affirmatam, ac proinde 3y3 - ayx esse negatam: aut quando 3xx - ay fuerit affirmata, tunc - 3y3 + ayx esse negatam, ac proinde 3y3 - ayx esse affirmatam. Per haec itaque apparet ex quantitatibus per regulam inuentis, quae erant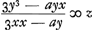 , judicari posse ad utrum casum constructio tangentis pertineat, nempe ex comperta dissimilitudine affectionis in divisore et dividendo, sequi ad priorem casum eam pertinere, hoc est z siue FE accipiendam esse versus A. Ex similitudine vero eorum affectionis sequi ad contrariam partem sumendam. , judicari posse ad utrum casum constructio tangentis pertineat, nempe ex comperta dissimilitudine affectionis in divisore et dividendo, sequi ad priorem casum eam pertinere, hoc est z siue FE accipiendam esse versus A. Ex similitudine vero eorum affectionis sequi ad contrariam partem sumendam.
 [Fig. 13]
Potest autem quantitas z siue FE, perregulam inuenta, nonnunquam ad simpliciores terminos reduci ope aequationis datae quae naturam curuae continet, velut in hac curua AC [Fig. 13] axem habente AD verticem A, cujusque ea est proprietas ut si a puncto C in ea sumpto applicetur ordinatim CD, fiat productum ex cubo BD (est autem B punctum in axe extra curuam datum) in quadratum DA aequale cubo quadrato DC. Siue ponendo BA ∞ a, BD ∞ x, DC ∞ y, fiat aequatio naturam curuae continens, x5 - 2ax4 + aax3 - y5 ∞ 0. Hic ponendo CG esse tangentem, quae occurrat axi in G, vocandoque DG, z. fit secundum regulam 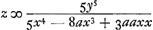 . quia autem ex data aequatione est ∞ y5 ∞ x5 - 2ax4 + aax3 restituendo pro 5y5 id quod ipsi aequale est fiet . quia autem ex data aequatione est ∞ y5 ∞ x5 - 2ax4 + aax3 restituendo pro 5y5 id quod ipsi aequale est fiet 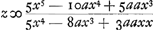 siue dividendo per xx erit siue dividendo per xx erit 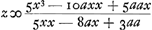 . Et rursus dividende hanc fractionem per x - a habebitur . Et rursus dividende hanc fractionem per x - a habebitur 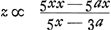 , quod significat faciendum ut sicut BD quinquies sumpta, minus BA ter, siue ut BA bis, una cum AD quinquies, ad AD quinquies, ita BD ad DG, atque ita GC tacturam in C curuam AC. , quod significat faciendum ut sicut BD quinquies sumpta, minus BA ter, siue ut BA bis, una cum AD quinquies, ad AD quinquies, ita BD ad DG, atque ita GC tacturam in C curuam AC.
|
|

