Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 228]
| |
Démonstration de la règle des maxima et des minima.
| |
[pagina 229]
| |
II. Demonstratio regulae de maximis et minimis.
| |
[pagina 230]
| |
Puisque AE = a et EG = x, on aura 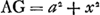 . Et puisque . Et puisque 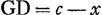 et BD = b, on aura et BD = b, on aura 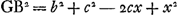 , de sorte que , de sorte que 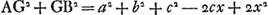 , expression que nous désignerons par les mots ‘termes antérieurs’. Ceci s'applique également à tout autre problème se rapportant à un maximum ou un minimum. D'autre part, lorsqu'on substitue partout dans l'équation trouvée x + e à x, (x + e)2 à x2 et ainsi de suite s'il s'y trouve quelque puissance plus élevée de x, il est certain qu'on obtiendra la somme FA2 + FB2. Celle-ci sera donc , expression que nous désignerons par les mots ‘termes antérieurs’. Ceci s'applique également à tout autre problème se rapportant à un maximum ou un minimum. D'autre part, lorsqu'on substitue partout dans l'équation trouvée x + e à x, (x + e)2 à x2 et ainsi de suite s'il s'y trouve quelque puissance plus élevée de x, il est certain qu'on obtiendra la somme FA2 + FB2. Celle-ci sera donc
a2 + b2 + c2 - 2cx - 2ce + 2x2 + 4ex + 2ee. Cette expression sera appelée ‘termes postérieurs’. Il faut l'égaler à AG2 + GB2. Nous aurons donc l'équation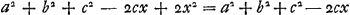 , d'où sortira la valeur EG ou x, GF ou e désignant une ligne de longueur donnée.
Or, en prenant e infiniment petite la même équation donnera la valeur de EG lorsqu'elle est égale à EF. De cette façon nous aurons déterminé le point cherché C pour lequel , d'où sortira la valeur EG ou x, GF ou e désignant une ligne de longueur donnée.
Or, en prenant e infiniment petite la même équation donnera la valeur de EG lorsqu'elle est égale à EF. De cette façon nous aurons déterminé le point cherché C pour lequel 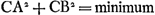 . Après avoir ôté d'abord les fractions s'il y en a (mais dans l'exemple considéré il n'y en a point), il faut supprimer de part et d'autre les termes égaux, lesquels sont nécessairement tous ceux qui ne contiennent pas la lettre e: on le comprend aisément puisque, comme nous l'avons dit, les termes posté- . Après avoir ôté d'abord les fractions s'il y en a (mais dans l'exemple considéré il n'y en a point), il faut supprimer de part et d'autre les termes égaux, lesquels sont nécessairement tous ceux qui ne contiennent pas la lettre e: on le comprend aisément puisque, comme nous l'avons dit, les termes posté-
| |
[pagina 231]
| |
Itaque quia AE ∞ a et AG ∞ x, erit quad. AG ∞ aa + xx. Et quia GD ∞ c - x et BD ∞ b, erit quad. GB ∞ bb + cc - 2cx + xx, unde quadrata AG, GB simul sumpta fient ∞ aa + bb + cc - 2cx + 2xx, qui dicantur termini priores; idque similiter in quouis alio problemate intelligendum, ubi maximum aut minimum inquiritur. Rursus autem quia EF ∞ x + e, si ubique in summa quadratorum inuenta substituam x + e pro x, et quadratum ab x + e pro xx, atque ita deinceps, si altior potestas ipsius x reperiatur, certum est exorituram summam quadratorum FA, FB quae quidem erit aa + bb + cc - 2cx - 2ce + 2xx + 4ex + 2ec aequanda summae quadratorum, AG, GB; dicantur autem hi termini posteriores. Itaque erit aa + bb + cc - 2cx + 2xx ∞ aa + bb + cc - 2cx - 2ce + 2xx + 4ex + 2ee ex qua aequatione prodibit valor EG siue x, quando GF siue e certae magnitudinis lineam refert. Ponendo autem e infinite paruamGa naar voetnoot2) apparebit ex eadem aequatione quanta futura sit EG cum ipsi EF aequalis est adeoque habebitur determinatio quaesita puncti C unde ductae CA, CB faciant summam quadratorum minimam, nempe sublatis primum fractionibus (si quae sint) quae in hoc exemplo nullae sunt, delentur termini qui utrinque ijdem habentur, quales sunt necessario omnes quibus littera e admixta non est, idque | |
[pagina 232]
| |
rieurs se tirent des termes antérieurs en substituant x + e à x dans toutes les puissances de cette dernière. Ensuite on divise tous les termes par e et on détruit ceux qui, après cette division, contiennent encore cette lettre, puisqu'ils représentent des quantités infiniment petites par rapport à ceux qui ne renferment plus e. C'est de ces derniers seuls qu'on tire enfin la quantité x satisfaisant au problème proposé. Telle est la méthode de Fermat; en l'abrégeant, j'ai trouvé la méthode suivante composée de deux parties. 1o. Lorsque les termes dont nous supposons qu'ils doivent posséder un maximum ou un minimum, ne comprennent aucune fraction contenant dans son dénominateur la quantité inconnue cherchée, il faut multiplier chaque terme par le nombre des dimensions que la quantité inconnue a dans ce terme, en négligeant les termes qui ne la contiennent point; et la somme de tous ces produits doit être égalée à zéro. Dans l'exemple proposé, où les termes antérieurs étaient a2 + b2 + c2 - 2cx + 2x2, somme de deux carrésGa naar voetnoot4bis) que je veux rendre minimale, il suffit donc d'effectuer la multiplication suivante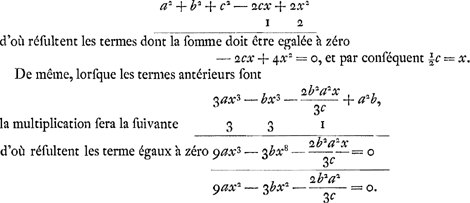 Pour comprendre la raison de ce procédé abrégé, il faut remarquer en premier lieu que, puisque les termes postérieurs se tirent des termes antérieurs en substituant partout x + e à x, tous les termes antérieurs se retrouvent nécessairement parmi les | |
[pagina 233]
| |
facile est intelligere, cum dixerimus posteriores terminos, ex prioribus describi, ponendo x + eGa naar voetnoot3) vel potestatem ejus, quoties invenitur x vel potestas ejus aliqua in prioribus. Deinde omnes termini per e dividuntur, quibusque post eam divisionem adhuc unum e aut plura inesse inueniuntur, ii delentur, quippe cum quantitates infinite paruas contineant, respectu coeterorum terminorum quibus nullum amplius inest e. Ex quibus denique solis inuenitur quantitas x quaesita in casu determinationis proposito; et haec est ratio methodi Fermatianae, quâ in compendium redactâ, hanc aliam inueni, cuius partes duae suntGa naar voetnoot4). nam primo Quando termini quos Maximum aut Minimum designare volumus, nullam fractionem habent, in cuius denominatore quantitas incognita quaesita continetur; multiplicandus est terminus quisque per numerum dimensionum quem in illo habet quantitas incognita, omissis terminis ijs in quibus incognita quantitas non reperitur; omniaque producta illa aequanda nihilo. Ita in exemplo proposito ubi termini priores inuenti sunt aa + bb + cc - 2cx + 2xx, summam quadratorum duorumGa naar voetnoot4bis) continentes, quam volo esse minimam, Hujus compendii ratio ut intelligatur, sciendum primò, quoniam termini posteriores ex prioribus describuntur, ponendo tantum ubique x + e pro x, necessario omnes | |
[pagina 234]
| |
termes postérieurs, de sorte qu'il est inutile de les écrire attendu qu'il faudrait immédiatement les supprimer, et que par conséquent il suffit d'écrire ceux qui contiennent e une ou plusieurs fois, comme dans le cas de notre exemple - 2ce + 4ex + 5e2, et d'égaler leur somme à zéro. Mais il appert en outre que les termes contenant e plus d'une seule fois seront eux aussi écrits inutilement, puisqu'il a été établi qu'après la division par e ils devront être supprimés, comme nous l'avons dit un peu plus haut. Il faut donc dès le début écrire comme termes postérieurs ceux-là seulement qui contiennent e une seule fois. Or, ces termes-là se déduisent facilement des termes antérieurs puisqu'il paraît que ce sont les deuxièmes termes des puissances de x + e, tous les autres termes de ces puissances contenant e ou plus d'une fois ou pas du tout. De sorte que partout où l'on trouve x dans les termes antérieurs il faut écrire x + eGa naar voetnoot5) dans les termes postérieurs, et où il y a x2 dans les antérieurs, 2ex dans les postérieurs; où il ya x3, 3ex2, etc. Mais lesdits deuxièmes termes de chaque puissance de x + e se tirent facilement de la puissance correspondante de x: il suffit de changer une lettre x en e et de mettre devant chaque terme le nombre des dimensions de x, de sorte que x2 ou xx devient 2ex et x3 se change en 3ex2 etc. Par conséquent on tire aisément les termes postérieurs dont nous avons dit que la somme doit être égalée à zéro des termes antérieurs contenant x (les seuls qu'il faille considérer, comme nous l'avons fait voir) en multipliant chacun d'eux par le nombre des dimensions de x. Car il n'est pas même nécessaire de changer une lettre x en e puisqu'il revient au même de diviser ensuite par e ou par x. Par ces considérations la raison de la méthode abrégée de la première partie de la règle est devenue évidente. Passons maintenant à la deuxième qui est la suivanteGa naar voetnoot6). 2o. Lorsque les termes dont nous voulons établir la valeur maximale ou minimale comprennent des fractions, dans le dénominateur desquelles se trouve la quantité inconnue, il faut d'abord supprimer les quantités connues, s'il y en a; ensuite, si les autres quantités n'ont pas le même dénominateur, il faut les y réduire. Après cela il faut multiplier chacun des termes qui constituent le numérateur de la fraction par chaque terme du dénominateur et multiplier chaque produit ainsi obtenu par la différence des dimensions de la quantité inconnue telle qu'elle se trouve respectivement dans le terme du numérateur et dans celui du dénominateur, en donnant à chaque produit le signe exigé par la règle de la multiplication lorsque le nombre des dimensions de la quantité inconnue dans le terme du numérateur surpasse celui du terme du dénominateur, et le signe contraire lorsqu'il en est autrement; enfin il faut égaler à zéro la somme de tous les termes obtenus. | |
[pagina 235]
| |
terminos priores etiam in posterioribus reperiri, ideoque illos nihil opus esse describi cum utrobique mox delendi forent, atque adeò illos tantum scribendos in quibus unum e vel plura insunt, ut in exemplo nostro - 2ce + 4ex + 2ee, eosque aequandos nihilo. Sed etiam illos quibus plura quam unum e inerunt, scribi frustra apparet, cum divisione facta per e delendos postea constet, ut paulo ante diximus. Itaque nulli praeterea ab initio describendi inter terminos posteriores, quam quibus inerit e simplex. Hi autem termini ex terminis prioribus facile deducuntur cum constet, nihil aliud esse quam secundos terminos potestatum ab x + e quia caeteri omnes plura quam unum e, vel nullum habent. Adeo ut ubicumque in prioribus terminis habetur x scribendum sit in posterioribus x + eGa naar voetnoot5) et ubi habetur xx in prioribus, ponendum 2ex in posterioribus, et ubi x3 in prioribus, in posterioribus 3exx atque ita deinceps. Dicti autem termini secundi cujusque potestatis x + e ex ipsa potestate x facile describuntur, mutando unum x in e, et praeponendo numerum dimensionum ipsius x; ita enim ab xx fit 2ex et ab x3, 3exx, atque in caeteris pari modo. Itaque ex terminis prioribus in quibus x, quos solos considerandos esse patuit, facile etiam termini posteriores ii quos nihilo adaequandos diximus, describuntur, multiplicando tantum singulos in numerum dimensionum quas in ipsis habet x. Nam mutare unum x in e ne quidum opus est, cum eodem redeat, siue omnes postea per e aut per x dividantur. Ex his quidem aperta est ratio compendii ad primam partem regulae pertinentis. nunc ad aliam veniamus quae est eiusmodiGa naar voetnoot6). Si terminis quos Maximum aut Minimum designare volumus fractiones habeant, in quarum denominatore occurrat quantitas incognita, delendae primum sunt quantitates cognitae, si quae adsint; deinde si reliquae quantitates non habeant eundem denominatorem, eo reducendae sunt. Tum termini singuli numeratorem fractionis constituentes ducendi in terminos singulos denominatoris, productaque singula multipla sumenda secundum numerum quo dimensiones quantitatis incognitae in termino numeratoris differunt a dimensionibus ejusdem incognitae quantitatis in termino denominatoris. Signa autem affectionis productis singulis praeponenda qualia lex multiplicationis exigit, quoties dimensiones quantitatis incognitae plures sunt in termino numeratoris, quam in termino denominatoris, at quoties contra evenit contraria quoque signa productis praeponenda, quae denique omnia aequanda nihilo. | |
[pagina 236]
| |
Supposons par exemple qu'on ait trouvé comme termes antérieurs que nous voulons saire acquérir une valeur maximale les suivants 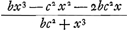 , où il n'y a pas de quantité connue. Suivant la règle je multiplie tous les termes du numérateur d'abord par bc2, et du premier produit obtenu, celui de bx3 par bc2, je prends le triple parce que bx3 a trois dimensions de la quantité inconnue x tandis que bc2 n'en a aucune; du deuxième produit, celui de - c2x2 par bc2, j'écris le double puisque dans - c2x2 il y a deux dimensions de x et aucune dans bc2; quant au troisième produit, celui de - 2bc2x par bc2, je l'écris simplement puisque dans - 2bc2x et bc2 la différence des dimensions de x est l'unité. Et je donne à ces trois produits leurs vrais signes puisque les dimensions de x dans les termes du numérateur surpassent celles du terme bc2 qui sont nulles. De sorte que ces trois produits sont , où il n'y a pas de quantité connue. Suivant la règle je multiplie tous les termes du numérateur d'abord par bc2, et du premier produit obtenu, celui de bx3 par bc2, je prends le triple parce que bx3 a trois dimensions de la quantité inconnue x tandis que bc2 n'en a aucune; du deuxième produit, celui de - c2x2 par bc2, j'écris le double puisque dans - c2x2 il y a deux dimensions de x et aucune dans bc2; quant au troisième produit, celui de - 2bc2x par bc2, je l'écris simplement puisque dans - 2bc2x et bc2 la différence des dimensions de x est l'unité. Et je donne à ces trois produits leurs vrais signes puisque les dimensions de x dans les termes du numérateur surpassent celles du terme bc2 qui sont nulles. De sorte que ces trois produits sont
3b2c2x3 - 2bc4x2 -2b2c4x. Ensuite je multiplie tous les mêmes termes du numérateur par x3, second terme du dénominateur. Or, je néglige le premier produit, celui de bx3 par x3, en d'autres termes je le multiplie par zéro, parce que les dimensions de x sont les mêmes de part et d'autre et que leur différence est donc nulle. Quant au deuxième produit de - c2x2 par x3, je l'écris simplement parce que pour ces termes-là la différence des dimensions de x est l'unité; et j'écris doublement le troisième produit, celui de - 2bc2x par x3, puisque la différence des dimensions de x y est 2. Je donne à ces deux derniers produits des signes contraires à ceux qu'exigerait la loi de la multiplication parce que dans les deux cas les dimensions de x sont moindres dans les termes du numérateur que celles de x3, terme du dénominateur. Les deux produits seront donc + c2x5 + 4bc2x4. En les ajoutant aux trois précédents + 3b2c2x3 - 2bc4x2 - 2b2c4x on obtient la somme qu'il faut égaler à zéro: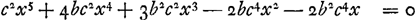 .
Divisant cette équation par c2bx + c2x2 on trouve .
Divisant cette équation par c2bx + c2x2 on trouve 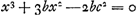 .
Ici aussi nous expliquerons à l'aide d'un seul exemple comment la règle a été obtenue: on comprendra qu'il en est de même dans tous les autres cas. Considérons donc les termes antérieurs proposés tantôt, savoir .
Ici aussi nous expliquerons à l'aide d'un seul exemple comment la règle a été obtenue: on comprendra qu'il en est de même dans tous les autres cas. Considérons donc les termes antérieurs proposés tantôt, savoir 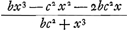 . Si j'en veux tirer, comme cela a été fait précédemment, en substituant x + e à x, d'autres termes auxquels je pourrai les comparer, je constate d'abord que parmi les termes postérieurs l'on peut négliger ceux qui contiennent plus d'une seule lettre e parce qu'il en résultera toujours des quantités contenant elles aussi plus d'une seule e et devant par conséquent être finalement supprimées pour la raison exposée plus haut. L'égalité des termes antérieurs et postérieurs sera donc exprimée par l'équation suivante: . Si j'en veux tirer, comme cela a été fait précédemment, en substituant x + e à x, d'autres termes auxquels je pourrai les comparer, je constate d'abord que parmi les termes postérieurs l'on peut négliger ceux qui contiennent plus d'une seule lettre e parce qu'il en résultera toujours des quantités contenant elles aussi plus d'une seule e et devant par conséquent être finalement supprimées pour la raison exposée plus haut. L'égalité des termes antérieurs et postérieurs sera donc exprimée par l'équation suivante: 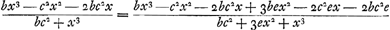 . .
| |
[pagina 237]
| |
Sint exempli gratia inventi termini priores quos maximum designare velimus isti 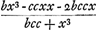 ubi nulla est quantitas cognita. Hic ergo secundum regulam multiplico terminos omnes numeratoris primum per bcc, priorisque producti ex bx3 in bcc scribo triplum, quia bx3 habet tres dimensiones quantitatis incognitae x, bcc vero nullam, secundi producti ex -ccxx in bcc, scribo duplum, propterea quod in -ccxx duae sunt dimensiones x et in bcc nullae; tertium vero productum ex -2bccx in bcc, scribo simplex quia in -2bccx et bcc differentia dimensionum x est unitas. Tribus autem hisce productis vera signa affectionis adscribo, quoniam dimensiones x in terminis numeratoris excedunt eas quae in termino bcc, quippe quae nullae sunt, ita ut tria haec producta sint ubi nulla est quantitas cognita. Hic ergo secundum regulam multiplico terminos omnes numeratoris primum per bcc, priorisque producti ex bx3 in bcc scribo triplum, quia bx3 habet tres dimensiones quantitatis incognitae x, bcc vero nullam, secundi producti ex -ccxx in bcc, scribo duplum, propterea quod in -ccxx duae sunt dimensiones x et in bcc nullae; tertium vero productum ex -2bccx in bcc, scribo simplex quia in -2bccx et bcc differentia dimensionum x est unitas. Tribus autem hisce productis vera signa affectionis adscribo, quoniam dimensiones x in terminis numeratoris excedunt eas quae in termino bcc, quippe quae nullae sunt, ita ut tria haec producta sint
3bbccx3 - 2bc4xx - 2bbc4x.
Iam porro terminos omnes eosdem numeratoris duco in x3 terminum alterum denominatoris primumque productum ex bx3 in x3 scribere omitto, siue per 0 multiplico, quoniam eaedem dimensiones utrobique sunt ipsius x, ideoque differentia nulla. Secundum autem productum ex -ccxx in x3 scribo simplex, quia in his terminis differentia dimensionum x est unitas; at tertium productum ex - 2bccx in x3 scribo duplum quia differentia dimensionum x in his est 2. Signa vero affectionis productis hisce duobus adscribo contraria ijs quae requireret lex multiplicationis, eo quod dimensiones x pauciores sunt utrobique in terminis numeratoris quam in x3 termino denominatoris. Itaque producta bina erunt haec +ccx5 + 4bccx4. quae addita tribus praecedentibus + 3bbccx3 - 2bc4xx - 2bbc4x faciunt summam aequandam nihilo ccx5 + 4bccx4 + 3bbccx3 - 2bc4xx - 2bbc4x ∞ 0 qua aequatione divisa per ccbx + ccxx fit x3 + 3bxx - 2bcc ∞ 0. Quomodo autem ad haec perventum sit, uno exemplo rursus explicabimus, ex quo eandem in omnibus caeteris rationem esse intelligetur. Videamus igitur priores terminos quos modo proposueram, nempe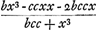 ex quibus si alios quibuscum eos comparem, ut initio factum est, describere velim, ponendo ubique x + e ubi est x, video quidem primo omnes illos in posterioribus terminis posse negligi in quibus plura quam unum e inerit, quia semper ex ijs quantitates orientur, in quibus plura uno e inerunt, quaeque proinde delendae tandem erunt, ob causam in superioribus traditam. Itaque erunt termini priores aequandi posterioribus ex quibus si alios quibuscum eos comparem, ut initio factum est, describere velim, ponendo ubique x + e ubi est x, video quidem primo omnes illos in posterioribus terminis posse negligi in quibus plura quam unum e inerit, quia semper ex ijs quantitates orientur, in quibus plura uno e inerunt, quaeque proinde delendae tandem erunt, ob causam in superioribus traditam. Itaque erunt termini priores aequandi posterioribus 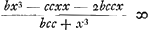 qui nempe ex prioribus hac lege descripti sunt, ut ubicunque est x vel potestas eius in prioribus ibi ponatur x + e, vel potestatis x + e duo priores termini; quoniam scimus in caeteris plura quam unum e contineri. qui nempe ex prioribus hac lege descripti sunt, ut ubicunque est x vel potestas eius in prioribus ibi ponatur x + e, vel potestatis x + e duo priores termini; quoniam scimus in caeteris plura quam unum e contineri.
| |
[pagina 238]
| |
Les termes postérieurs y sont tirés des termes antérieurs en substituant partout à x ou ses puissances x + e ou les deux premiers termes des puissances de x + e, puisque nous savons que dans les termes ultérieurs il y a plus d'une seule lettre e. Or, comme les termes sans e dans les numérateurs des termes antérieurs et postérieurs sont absolument les mêmes, il appert que de part et d'autre les multiplications des termes sans e des dénominateurs avec les termes sans e des numérateurs peuvent être omises, parce qu'il en résulterait de part et d'autre des quantités égales qui se détruiraient. C'est pourquoi il suffisait d'écrire dès le commencement comme termes postérieurs ceux-là seulement qui contiennent une seule lettre e en négligeant tous les autres; de sorte que l'équation devient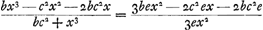 . .
Maintenant il faudrait donc faire les multiplications croisées pour se débarrasser des fractions. Mais en examinant avec quelqu'attention quels seront les résultats de ces multiplications, nous trouverons encore un nouvel abrègement: nous découvrirons qu'il n'est point du tout nécessaire d'écrire les termes postérieurs. En effet, comme ils découlent des termes antérieurs par le changement d'une lettre x en e et l'addition d'un facteur égal au nombre des dimensions de x, il n'est pas difficile de conclure des termes antérieurs seulement quels seront tous ces produits. Par exemple la présence de -c2x2 dans les termes antérieurs donnant lieu à celle de -2c2ex dans les termes postérieurs, et celle de x3 dans le premier dénominateur à celle de 4ex2 dans le second, on voit aisément que les deux produits, celui de -c2x2 par 3ex2, et celui de -2c2ex par x3, qui sont -3c2ex4 et -2c2ex4, seront composés des mêmes lettres, mais que les facteurs 3 et 2 seront différents, et que cette dernière différence résulte du fait que x dans le terme c2x2 a une dimension de moins que dans le terme x3. Supprimant ensuite -2c2ex4 dans les deux membres de l'équation, il appert qu'il restera -c2ex4 du côté des termes antérieurs. C'est ce qu'on peut donc obtenir de suite en multipliant simplement dans les termes antérieurs le -c2x2 du numérateur avec le x3 du dénominateur, en changeant dans le produit une lettre x en e, et en écrivant le produit simplement puisque dans ces deux termes la différence des dimensions de x est l'unité. De la même manière les produits de -2bc2x par 3ex2 et de -2bc2e par x3, lesquels ont les mêmes lettres, étant -6bc2ex3 et -2bc2ex3, auront des facteurs numériques différents parce que dans -2bc2x il n'y a qu'une seule dimension de x, tandis qu'il y en a trois dans x3; soustrayant -2bc2ex3 de part et d'autre de l'équation, je constate qu'il reste - 4bc2ex3 du côté des termes antérieurs, ce qui pouvait de nouveau être aperçu dès le début puisque la même quantité provient de la multiplication du terme - 2bc2x du premier numérateur par le terme x3 du dénominateur lorsque dans le produit on remplace une lettre x par e et qu'on y ajoute le facteur 2 qui exprime la différence des dimensions de x dans les termes - 2bc2x et x3. Mais comme dans les termes bx3 et x3 la dimension de x est la même, il s'ensuit que | |
[pagina 239]
| |
Iam vero porro quia termini in quibus nullum e in numeratore ac denominatore priorum ac posteriorum terminorum ijdem plane reperiuntur, patet multiplicationes alternas eorum terminorum denominatoris in terminos numeratoris partis alterius e carentes omitti posse, cum quantitates inde ortae, eaedem utrinque essent futurae, ideoque delendae. Quare in terminis posterioribus tantum ij ab initio scribendi erant, in quibus unum e, omissis omnibus reliquis; ut aequatio hic futura sit ista 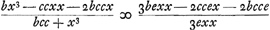 . .
Hic jam multiplicationes alternae per denominatores instituendae essent ad tollendas fractiones, verum examinando diligentius quaenam futura sint earum multiplicationum producta, aliud adhuc compendium inueniemus, et nec scribendos quidem omnino esse terminos posteriores; quia enim describuntur ex prioribus mutato x in e, praepositoque numero dimensionum ipsius x, non difficile est colligere ex solis terminis prioribus quaenam futura sint omnia ista producta. Ita quoniam propter - ccxx in prioribus habetur - 2ccex in posterioribus, et propter x3 in denominatore priorum, in posteriorum denominatore est 3exx, facile perspicitur utraque producta ex - ccxx in 3exx et ex - 2ccex in x3 quae sunt - 3ccex4 et - 2ccex4, easdem literas habitura, sed diversos numeros praepositos 3 & 2; idque inde fieri quod in termino ccxx unam dimensionem minus habeat x quam in termino x3. Itaque et auferendo postea ex utraque parte aequationis - 2ccex4, apparet superfuturum -ccex4 a parte terminorum priorum. Quare ab initio hoc sciri potest, multiplicando tantum in terminis prioribus - ccxx numeratoris in x3 denominatoris, unumque x in e mutando, ac productum simplex scribendo quia differentia dimensionum x in istis duobus terminis est unitas. Eadem ratione producta ex - 2bccx in 3exx et ex -2bcce in x3 quae easdem litteras habent, sunt enim - 6bccex3 et - 2bccex3, habebunt numeros praepositos diversos, propterea quod in - 2bccx una tantum est dimensio x, at in x3 tres, unde ablato ex utraque parte aequationis - 2bccex3, scio superfuturum a parte terminorum priorum - 4bccex3, quod rursus ab initio cognosci potuit quia eadem quantitas oritur multiplicando - 2bccx numeratoris terminorum priorum in x3 denominatoris, mutandoque unum x in e et productum multiplicando per 2 quae est differentia dimensionum x in terminis - 2bccx et x3. At quoniam in bx3 et in x3 eadem est dimensio x, sequetur producta ex bx3 in 3exx et ex 3bexx in x3 tum literas easdem, tum eosdem numeros praepositos habitura, ideoque sese mutuo sublatura, ut proinde multiplicatio illa possit omitti. Atque eiusmodi animadversionibus inuentum quod in regula praecipitur, terminos singulos numeratoris in singulos denominatoris terminos esse ducendos, productaque quaelibet multipla sumenda secundum differentiam dimensionum quantitatis incognitae, in terminis binis, qui in se mutuo ducuntur. Nam quod non praecipitur unum x in e mutandum, id hanc rationem habet, quod non referat utrum postea per e an per x termini dividantur. | |
[pagina 240]
| |
les produits de bx3 par 3ex2 et de 3bex2 par x3 auront non seulement les mêmes lettres, mais aussi les mêmes facteurs numériques et que par conséquent ils se détruiront, de sorte que cette multiplication peut être omise. C'est par des remarques de cette sorte qu'a été trouvé ce qui est prescrit dans la règle, savoir que les différents termes du numérateur doivent être multipliés par ceux du dénominateur, et que chaque produit doit être multiplié par un facteur résultant de la différence des dimensions de l'inconnue dans les deux termes qui forment le produit. Il n'y est pas dit qu'il faut changer une lettre x en e; en effet, il n'importe que la division qui doit suivre soit faite par e ou bien par x. Quant au précepte suivant lequel il faut donner à chaque produit le vrai signe toutes les fois que les dimensions de x dans le numérateur sont supérieures en quantité à celles de x dans le dénominateur, ceci aussi pourra être compris d'après ce que nous avons dit; et par conséquent aussi qu'il faut donner les signes contraires lorsque le contraire est vrai pour les nombres des dimensions. Ici par exemple le produit de bx3 par bc2 doit être écrit avec le signe - et le facteur 3, de sorte qu'il vient - 3b2c2x3; en effet, à cause de bx3 nous savons que nous aurons 3bcx2 dans les termes postérieurs, ce qui multiplié par bc2 fera + 3b2c2ex2, mais transporté dans la partie antérieure de l'équation, ceci deviendra - 3b2c2ex2, ou bien, si l'on ne change pas x en e, - 3b2c2x3Ga naar voetnoot8). Enfin, l'exemple suivant fera voir que la règle enseigne à bon droit que toutes les fois qu'il y a des termes connus parmi les termes antérieurs avant leur réduction à un dénominateur commun, il faut commencer par les supprimerGa naar voetnoot9). Supposons qu'on ait trouvé les termes antérieurs suivants devant avoir une valeur maximale ou minimale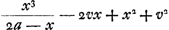 , où v2 désigne une quantité connue. Pour qu'il apparaisse que v2 doit être supprimé, voyons ce qui se passera si l'on ne supprime point ce terme, auquel cas, pour le réduire au dénominateur commun, il faudra le multiplier par 2a - x, de sorte qu'il viendra , où v2 désigne une quantité connue. Pour qu'il apparaisse que v2 doit être supprimé, voyons ce qui se passera si l'on ne supprime point ce terme, auquel cas, pour le réduire au dénominateur commun, il faudra le multiplier par 2a - x, de sorte qu'il viendra 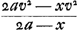 dans les termes antérieurs. Pour lesquels il faudra, suivant l'explication donnée plus haut, écrire dans les termes postérieurs dans les termes antérieurs. Pour lesquels il faudra, suivant l'explication donnée plus haut, écrire dans les termes postérieurs 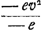 ; par conséquent dans la multiplication croisée il faudra multiplier 2a - x par -ev2 d'un côté, et de l'autre -e par 2av2 - xv2; or, les mêmes termes résulteront nécessairement des deux multiplications, puisque des deux
côtés on multiplie continuellement les mêmes facteurs 2a - x, -e, et v2. Ces termes se détruiraient donc et seraient par conséquent écrits inutilement: il en résulte qu'on peut en toute sécurité supprimer directement la quantité v2. Et, en examinant diligemment la chose, on apercevra clairement qu'il doit en être de même dans tous les autres cas. ; par conséquent dans la multiplication croisée il faudra multiplier 2a - x par -ev2 d'un côté, et de l'autre -e par 2av2 - xv2; or, les mêmes termes résulteront nécessairement des deux multiplications, puisque des deux
côtés on multiplie continuellement les mêmes facteurs 2a - x, -e, et v2. Ces termes se détruiraient donc et seraient par conséquent écrits inutilement: il en résulte qu'on peut en toute sécurité supprimer directement la quantité v2. Et, en examinant diligemment la chose, on apercevra clairement qu'il doit en être de même dans tous les autres cas.
| |
[pagina 241]
| |
Quod vero signaGa naar voetnoot7) affectionis vera productis singulis praeponenda dicuntur quoties dimensiones x plures sunt in numeratore quam in denominatore; id quoque ex jam dictis intelligetur; uti consequenter etiam hoc, quod contraria signa sunt apponenda quoties dimensionum numerus contra se habet. Velut hic productum ex bx3 in bcc scribendum est cum signo - proposito numero 3 ut fiat - 3bbccx3Ga naar voetnoot8), quia nempe propter bx3 scimus in posterioribus terminis fore 3bcxx, quod ductum in bcc faciet + 3bbccexx sed translatum in partem priorem aequationis fiet - 3bbccexx, siue, non mutato x in e, - 3bbccx3Ga naar voetnoot8). Quod denique in Regula habetur, quoties in prioribus terminis priusquam ad eundem denominatorem reducantur, quantitates cognitae occurrunt, eas primum omnium delendas; id ex sequenti exemplo intelligetur recte praecipiGa naar voetnoot9). Sint enim reperti termini priores, quos maximum aut minimum designare oporteat, isti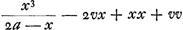 , ubi vv quantitatem cognitam significet. Id igitur delendum esse ut appareat, videamus quid futurum sit, si non deleatur, nempe ut ad eundem denominatorem cum caeteris omnibus reducatur, ducendum vv in 2a - x, fietque inde , ubi vv quantitatem cognitam significet. Id igitur delendum esse ut appareat, videamus quid futurum sit, si non deleatur, nempe ut ad eundem denominatorem cum caeteris omnibus reducatur, ducendum vv in 2a - x, fietque inde 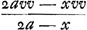 in terminis prioribus. Propter quos in terminis posterioribus, secundum superius explicata, scribetur in terminis prioribus. Propter quos in terminis posterioribus, secundum superius explicata, scribetur 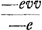 adeoque multiplicatione, alternatim utrinque per denominatores instituta, ducendum erit hinc 2a - x in -evv, inde -e in 2avv - xvv, ex quibus multiplicationibus eosdem utrinque terminos oriri necesse est, cum utrobique eadem haec tria in se mutuo ducantur 2a - x in -e in vv, qui proinde termini sese mutuo sublaturi essent, eoque frustra scriberentur; ac proinde liquet tuto deleri posse ab initio quantitatem vv. Idemque quod in hoc exemplo accidit, necessario quoque in quibuslibet alijs contingere diligenter intuenti manifestum erit. adeoque multiplicatione, alternatim utrinque per denominatores instituta, ducendum erit hinc 2a - x in -evv, inde -e in 2avv - xvv, ex quibus multiplicationibus eosdem utrinque terminos oriri necesse est, cum utrobique eadem haec tria in se mutuo ducantur 2a - x in -e in vv, qui proinde termini sese mutuo sublaturi essent, eoque frustra scriberentur; ac proinde liquet tuto deleri posse ab initio quantitatem vv. Idemque quod in hoc exemplo accidit, necessario quoque in quibuslibet alijs contingere diligenter intuenti manifestum erit.
|
|


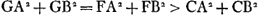 .
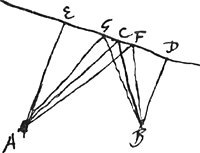
Pour trouver C de telle manière que CA2 + CB2 = minimum, je me figure d'abord que, AE et BD ayant été menées perpendiculairement à ED (je pose AE = a, BD = b, ED = c), la différence des deux droites EG et EF soit égale à une ligne donnée e; et je demande quelle doit être la valeur de EG, que j'appelle x, pour qu'on ait
.
Pour trouver C de telle manière que CA2 + CB2 = minimum, je me figure d'abord que, AE et BD ayant été menées perpendiculairement à ED (je pose AE = a, BD = b, ED = c), la différence des deux droites EG et EF soit égale à une ligne donnée e; et je demande quelle doit être la valeur de EG, que j'appelle x, pour qu'on ait 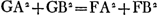 .
.