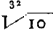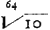Oeuvres complètes. Tome XX. Musique et mathématique

[p. 225]

I. Regle pour trouuer les logarithmes¹⁾.
[1666 ou 1667]

Registres de l'Académie Royale des Sciences, T. II²⁾, p. 40-42.

(Voyez sur une rédaction antérieure de cette règle, datant apparemment de 1661, comme celle du Manuscrit B mentionnée dans la note 1, l'Appendice II à la p. 295 qui suit).

Le calcul suiuant cette regle est beaucoup plus court que par celle dont on s'est servy iusques icy, et pour faire uoir la difference il faut seulement remarquer que pour trouuer par exemple le Logarithme de 2 iusques a 10. chiffres vrais, il falloit extraire enuiron quarante fois la racine quarrée d'un nombre de 64. chiffres, la ou par la presente regle pour auoir le mesme Logarithme, il ne faut qu'extraire 6. fois la racine quarrée d'un nombre de 28. chiffres, et faire ensuitte trois divisions, et une multiplication.

La Regle est celle cy.

Il faut auoir une fois pour tout les racines quarrées du nombre 10. extraites consecutiuement iusques a la sixiesme, et chaque racine de 14. chiffres, si³⁾ l'on desire auoir les Logarithmes iusqu'a 10. characteres ueritables, ou iusque la septieme ou 8^e.

1) Voyez sur cette Règle les p. 431-434 du T. XIV. La Pièce correspondante du Manuscrit C (p. 110-111) - que nous avons déjà mentionnée dans la note 1 de la p. 452 du T. XIV - porte la date du 2 novembre 1666 [2 Nov. 1666. Ex libro B. Le Fundamentum regulae nostrae ad inveniendos logarithmos du Manuscrit B (p. 17-19) date déjà d'août 1661. Voyez la p. 451 du T. XIV]. Les quelques différences entre cette Pièce et celle des Registres sont absolument insignifiantes (voyez cependant la note 7 de la p. 227). Huygens l'a sans doute copiée, et ce doit être une copie de sa copie qui a été insérée dans les Registres. D'après la place qu'elle occupe dans les Registres cette dernière copie doit dater du commencement de 1667 (ou peut-être de la fin de 1666).

2) Voyez sur le T. II, intitulé ‘Registres de Mathematiques de l'année 1667 et d'une partie de l'année 1668 jusqu'au mois d'Auril,’ les l. 4-5 de la p. 180 du T. XIX.

3) Le copiste avait écrit à tort ‘et si’. Le texte du Manuscrit C est correct.

[p. 226]

racine, et dauantage (et quand et quand⁴⁾ de plus de chiffres si l'on les ueut encore plus precisement): et de ces racines l'on n'a qu'a considerer les deux dernieres. Ainsy

La racine 5^e. extraitte de 10⁵⁾ est 10746078283213. qui soit appellée a [nous remplaçons les quelques majuscules du texte des Registres par des minuscules; Huygens - ou bien plutôt le copiste; voyez les notes 1 et 3 - se sert indiff éremment des deux].

La racine 6^e.⁶⁾ est 10366329284377. qui soit b.

L'unité 10000000000000. qui soit d, c'est a dire estant multipliée par 1⑬, comme le sont aussy les dites racines pour faire en aller les fractions.

Maintenant il faut trouuer un nombre égal a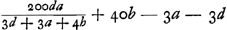 , lequel nombre est icy 559661035184532. On le multipliera par a - d dont le produit sera 4175509443116778 &c, dont il sera assés de prendre ces premiers characteres; et il faut noter que ce nombre une fois trouué seruira ensuitte au calcul de tous les Logarithmes.

Soit proposé de trouuer le Logarithme de 2. Il faut auoir semblablement la 5^e et 6^e racine extraite de 2. en 14. chiffres, comme auparauant du nombre 10.

La 5^e. racine de 2. est 10218971486541. qui soit dite f.

La 6^e. racine de 2. est 10108892860517. qui soit dite g.

Et l'unité comme deuant 10000000000000. soit d.

Il faut apres trouuer un nombre egal a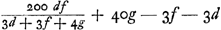 , lequel nombre est icy 545869542830178. On le multipliera par a - ad/f, et le produit sera 12569535892606. &c.

Maintenant comme le nombre dessus trouué 41755&c a cettuy cy 12569&c, ainsy sera le Logarithme de 10. a scavoir 100000&c. au logarithme de 2. qui sera 0,30102999567; ou il y a 10. characteres vrais, et l'unziesme qui surpasse le vray de l'unité. L'on scait qu'il faut mettre un zero pour characteristique a cause que le nombre 2. est au dessous de 10.

Or pour trouuer le Logarithme d'un nombre au dessus de 10, il faut tant de fois extraire continuellement la racine quarrée, que la derniere extraite soit moindre que

4) Manucrit C: quant et quant.

5) C.à.d. .

6) C.à.d. .

[p. 227]

la racine sixiesme extraite de 10. c'est a dire aux nombres depuis 10. iusqua 100. il faudra extraire 7. fois. Depuis 100. iusqua 10000. huit fois. Depuis 10000 à 100000000 neuf fois. Et en se seruant des deux racines dernieres, et les appelant f et g et operant comme dessus, l'on aura le Logarithme de la racine qui est la 7^e en comptant de la derniere en arriere, et cela aussy precisement que nous auons trouué le Logarithme de 2. c'est a dire iusqua 10. characteres vrais. Doublant apres ce logarithme trouué l'on aura celuy du nombre proposé, si l'on n'a fait que 7. extractions ou doublant encore une fois, si l'on a fait 8. extractions, et encore une fois si l'on en a fait 9⁷⁾.

Registres, T. I⁸⁾, p. 246. le 26 Octobre 1667 ... Mr. Auzout prendra la peine de disposer le trauail de Messieurs Auoye⁹⁾, Richer, et Niquet pour faire des Logarithmes¹⁰⁾.

7) La Pièce du Manuscrit C - voyez la note 1 de la p. 225 - ajoute: Par exemple, pour trouver le logarithme du nombre premier 7859 il faut avoir la 7^e et 8^e racine de ce nombre, qui soient nommees n, o, p, q, r, s, f, g, et le logarithme que l'on trouvera sera celuy de la racine o, qui est la 7^e en commencant par la derniere g. Et doublant ce logarithme on aura celuy de la racine n. Et doublant encore ce dernier logarithme on aura celuy du nombre proposè 7859.

8) Voyez l'endroit du T. XIX cité dans la note 2 de la p. 225. Le ‘T. I.’ est intitulé ‘Registre de physique 1667 et une partie de 1668’. Sur le dos on lit en outre ‘1666, 1667. 1668’.

9) Faut-il lire ‘de la Voye’ (voyez sur lui le T. XVIII)? Dans la brochure de 1938 de M. Harcourt Brown ‘l'Académie de physique de Caen (1666-1675) d'après les lettres d'André de Graindorge’ (Caen, Le Tendre) nous trouvons à la p. 21 le passage suivant d'une lettre de Graindorge du 7 mai 1668: ‘Notre assemblée physique a été différée à aujourd'hui ... A la dernière, où assistèrent Mr. Vogel [c.à.d. Martin Fogel, médecin d'Hambourg] et autres Allemands avec Mr. Avoye, nous éprouvâmes, etc.’ M. Brown nous écrit ne pas savoir qui était ce Mr. Avoye.

10) Il paraît donc qu'à l'Académie on a calculé des logarithmes suivant la méthode de Huygens.