Oeuvres complètes. Tome XX. Musique et mathématique

[p. 188]

II.¹⁾ l'Incommensurable.

7 Jan. 1675.

Diameter quadrati incommensurabilis est ejusdem lateri.

Sit quadratum cujus latus AC, diameter AB [Fig. 5]. Dico AB, AC incommensurabiles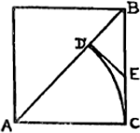

[Fig. 5]

esse. Si enim non, sunto si possunt commensurabiles. Erunt ergo ut numerus ad numerum.

Sit AB ad AC ut numerus FG ad FH [Fig. 6] integer uterque.

Les deux derniers mots ont été ajoutés dans l'interligne. Dans le premier alinéa Huygens prenait le mot ‘numerus’ dans le sens du grec ἀριϑμός, nombre entier²⁾. Ses ‘numeri integri’ sont opposés aux nombres fractionnaires²⁾. Nous n'avons pas trouvé que Huygens parle de nombres incommensurables³⁾. Le ‘nombre π’ date de plus tard⁴⁾. Il est vrai qu'il parle parfois de nombres sourds⁵⁾ ou irrationnels⁶⁾ - comme on faisait assez généralement longtemps avant lui⁷⁾ - et que déjà en 1661 (voyez la p. 12 qui précède) il accorde le nom de ‘nombres’ aux logarithmes. Voyez encore sur les nombres sourds etc. la p. 370 qui suit.

Porro centro A radio AC descripta circumferentia secet diametrum in D, unde

1) Portef. ‘Physica varia’, f. 11 v.

2) C.à d. dans le sens que les mathématiciens grecs (antérieurs à Diophante qui admet les nombres fractionnaires) donnent à ce mot; chez Aristote - voyez la note 27 de la p. 181 qui précède - le mot ἀριϑμός est appliqué aussi à une quantité qui varie d'une manière continue, le temps.

2) C.à d. dans le sens que les mathématiciens grecs (antérieurs à Diophante qui admet les nombres fractionnaires) donnent à ce mot; chez Aristote - voyez la note 27 de la p. 181 qui précède - le mot ἀριϑμός est appliqué aussi à une quantité qui varie d'une manière continue, le temps.

3) Comme on pourrait le croire d'après la l. 2 d'en bas de la p. 245 du T. XII. Voyez les l. 4-5 de la p. 126 du T. XIV (datant de 1675), avec la note 6.

4) Comparez la note 3 de la p. 372 du T. XVI.

5) L. 12 de la p. 273 du T. VI (dispute avec Gregory sur la question de la quadrature du cercle, 1668).

6) Voyez la p. 244 du T. VIII (correspondance avec Leibniz, 1679).

7) Ludolf van Ceulen p.e. parle de ‘irrationale ghetallen’ dans son ouvrage ‘De Arithmetische en Geometrische fondamenten’ de 1615: voyez la note 3 de la p. 93 du T. XII.

[p. 189]

ducta DE perpendicularis AB occurrat lateri CB in E. Sunt ergo ED, EC aequales quia ab eodem puncto E egredientes circumferentiam CD tangunt. Quia autem AB ponitur ad AC sive ad AD ut numerus GF ad numerum FH. [Fig. 6] erit et AD ad reliquam DB ut numerus FH ad numerum HG. Sed

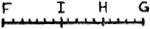[Fig. 6]

DB est aequalis DE sive EC, et AD aequalis AC sive BC. Ergo et BC ad CE ut numerus FH ad HG. Auferatur ab FH numerus HI aequalis HG. Ergo BC ad CE ut numerus FH ad HI. Et BE ad EC ut numerus FI ad IH. Est autem quadratum BE duplum quadrati BD, propter similes triangulos ABC, EBD⁸⁾. Ergo quadratum BE duplum quoque quadrati EC. Et quadratum numeri FI duplum quadrati ab IH. Apparet ergo, positis numeris integris GF, FH, quorum illius quadratum sit hujus quadrati duplum, dari necessario duos alios minores numeros integros FI, IH quorum unius quadratum sit alterius duplum. Itaque positis FI, IH, alij duo his minores numeri integri dabuntur quorum quadrata similiter duplam proportionem servent. Atque ita in infinitum. Quod est absurdum quia numeri integri descendendo infiniti non sunt. Non sunt ergo AB, AC commensurabiles.

Potest et aliter perfici demonstratio: si FG et FH ponantur numeri minimi inter se rationem AB ad AC habentes. Ostendetur enim uti prius numeros existere FI, IH minores quam GF, FH, quorumque eadem inter se ratio quam AB ad AC; quod absurdum, cum positi sint GF, FH minimi eorum qui istam rationem inter se obtinent.

8) Le théorème de Pythagore est donc supposé connu, du moins pour le triangle rectangle équilatère.