Oeuvres complètes. Tome XX. Musique et mathématique
(1940)–Christiaan Huygens–
[pagina 49]
| |||||||||||||||||||||||||||||||||||||||||||||||||
BGa naar voetnoot1). Divisio monochordi I.
| |||||||||||||||||||||||||||||||||||||||||||||||||
| V | a | L | 2x3/aa |
| V♯ | 16x7/a6 | ♭ | a3/4xx |
| R | 2xx/a | C | 4x5/a4 |
| M♭ | a4/4x3 | V2 | ½ a |
| M | 4x4/a3 | V2♯ | 8x7/a6 |
| F | aa/2x | R2 | xx/a |
| F♯ | 8x6/a5 | R2♯ | a4/8x3 |
| S | x | M2 | 2x4/a3 |
| S♯ | 16x8/a7 | F2 | aa/4x |
| a5/8x4Ga naar voetnoot3) | |||
8 Jul. 1661.
§ 1. Sit tota chorda VP partium aGa naar voetnoot2). SP putetur sonare diapente ad VP, et esse SP partium x. huic alia similis diapente putetur SR2. Ergo ut a ad x ita x ad xx/a ∞ R2 hoc est R2P. Ergo R diapason R2 erit 2xx/a. huic rursus fiat similis diapente RL, ergo ut a ad x ita 2xx/a ad 2x3/aa ∞ L. huic rursus similis diapente sit LM2. Ergo ut a ad x, ita 2x3/aa ad 2x4/a3 ∞ M2. Unde M diapason M2 erit 4x4/a3. huic rursus diapente sit MC. Ergo ut a ad x ita 4x4/a3 ad 4x5/a4 ∞ C. Iam quia SV2 est diatessaron sumatur ei similis diatessaron VF. Nempe ut x ad ½a ita sit a ad aa/2x ∞ F. ab F ad ♭ sumatur similis item diatessaron, fit ♭ ∞ a3/4xx. Porro tertiae majori VM sumatur similis tertia
RF♯. fit F♯ ∞ 8x6/a5. item similis istis MS♯ fit S♯ 16x8/a7. Item LV2♯. fit V2♯ ∞ 8x7/a6. unde diapason ejus nempe V♯ ∞ 16x7/a6. Rursus ab R2 sumatur tertia major deorsum R2♭, fit ♭ ∞ a3/4xx. Similiter tertia major SM♭; fit M♭ ∞ a4/4x3. atque ita omnes toni ac semitoni reperti suntGa naar voetnoot4).
Erunt autem ex constructione diapente similes VS, SR2, RL, LM2, MC. sed et similis illis V♯S♯. item M♭C♭Ga naar voetnoot5), CF2♭, item ♭F2. Item FV2, F♯V2♯. omnes enim uti a ad x. sunt ergo 11; quare dissimilis 1, S♯M♭Ga naar voetnoot6).
Diatessaron similes sunt ex constructione SV2, VF, F♭; siunt autem similes et istae V♯F♯, RS, ML, F♯ C, S♯V2♯, LR2, C♭M♭2, CM. omnes enim ut x ad ½a, five 2x ad a. Sunt ergo 11; et dissimilis 1Ga naar voetnoot7). Tertiae majores similes ex constructione VM, RF♯, MS♯, LV2♯, ♭R2, R♯SGa naar voetnoot8). fiunt autem et istae FL,SC. omnes enim ut a4 ad 4x4. Sunt ergo 8, et dissimiles 4.Ga naar voetnoot9).
Tertiae minores similes fiunt VR♯, V♯M, RF, MS, F♯L,S♭, S♯C, LV2, CR2. Sunt ergo 9 et dissimiles 3Ga naar voetnoot10).
Sextae majores similes sunt VL,RC,R♯V2Ga naar voetnoot11), MV2♯,FR2,SM2,LF2♯,♭S2, CS♯2. Nempe sunt complementa tertiarum minorum. Ergo 9 similes, et 3 dissimilesGa naar voetnoot12).
Sextae minores similes sunt V♯L,R♭,MV2, F♯R2, SR2♯, S♯M2,LF2,CS2, nempe 8, complementa tertiarum majorum. Reliquae dissimiles 4Ga naar voetnoot13).
§ 2. Horum omnium intervallorum indeterminata est hactenus magnitudo, nam
qualiscunque adsumatur x, similitudo dicta ubique locum habebit. (En marge: omnes toni aequales VR; RM; FS; SL; LC. item MF♯; F♯S♯; CV♯). Videamus ergo quanta convenientissime possit statui x. Sane si ponatur x ∞ ⅔a, constat quintas omnes ac proinde et quartas perfectas fore. Verum tunc fit VL ∞ 2x3/aa ∞ 16/27 a. Sed ut sit perfecta sexta major VL, deberet esse L ∞ ⅗ a, quod majus est quam 16/27 a. Ergo ratio LP ad VP minor est vera ad efficiendam sextam majorem, quamobrem sexta haec major erit justo. atque ita omnes reliquae sextae majores supra enumeratae, quia omnes inter se sunt similes. Hinc vero et tertiae minores omnes supradictae, quae sunt complementa sextarum majorum erunt minores justoGa naar voetnoot14). Differentia autem erit 1/80Ga naar voetnoot15) id quod comma vocant, nam 16/27 est ad ⅗ ut 80 ad 81. quae valde est notabilis, ita ut facile imperfectio ejusmodi tertiarum ac sextarum aure percipiatur. Est enim comma 1/9 toni proximeGa naar voetnoot16).
Sed et tertia major VM ex illa positione, nempe si x sit ∞ ⅔a, major vera contingit, est enim M ∞ 4x4/a3 ∞ 64/81 a, cum debeat esse ⅘a ad faciendam consonantiam tertiae majoris. Estque 64/81 ad ⅘ ut 80 ad 81. quae rursus notabilis est commatis differentia, qua etiam sextae minores à veris deficient, quippe tertiarum majorum complementa. Praestat igitur quintam VS paulo minorem vero sumere, hoc est x paulo majorem quam ⅔a. hinc enim video sextam majorem VL et omnes similes minorem factum iri quam prius, crescente nempe L quae erat 2x3/aa. videoque simul tertiam majorem VM decrescere sicut requiritur, nam etiam 4x4/a3 major efficitur dum major ponitur x. quanto igitur majorem sumimus x quam ⅔a? Optimum videtur ut ita comparetur si fieri possit, ut quintae tanto minores evadant perfectis quanto sextae majores veras excedent.

differentia ergo est 1/480 proximè totius chordaeGa naar voetnoot17) qua x sive SP debet major sumi quam ⅔a. quae differentia est valde exigua.
Omnes igitur tertiae majores et sextae minores similes, sunt perfectae in hoc systemate. Quintae vero et tertiae minores pauxillo minores sunt veris, aequali defectuGa naar voetnoot18). nam chordae partes quae sonant quintas vel tertias minores contra tonum aliquem graviorem excedunt veras proximè 1/320 sui parteGa naar voetnoot19); accurate autem quartâ parte commatis. Quartae autem, et sextae majores tantundem veras superantGa naar voetnoot20).
En marge: dico id quo S nostrum temperatum distat ab S vero sive ⅔a esse accurate ¼ commatis, nam ratio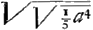 sive x ad ⅔a quadruplicata facit rationem ⅕a4 ad 16/81 a4 hoc est ut 81 ad 80, quae est commatis.
sive x ad ⅔a quadruplicata facit rationem ⅕a4 ad 16/81 a4 hoc est ut 81 ad 80, quae est commatis.
Notandum etiam tonos omnes istos aequales esse VR,RM,M♭F, MF♯, FS, F♯S♯, SL, LC,C♭V2,CV2♯. Dissimiles tantum V♯R♯,S♯C♭Ga naar voetnoot21).Semitonia majora similia V♯R, RM♭,MF,F♯S,S♯L,LC♭,CV2. Reliqua quinque minora etiam inter se similia VV♯, M♭M,FF♯,SS♯,C♭C.
§ 4. Si velimus ut tertiae minores majoresque, et sextae majores minoresque aeque multum a veris distent
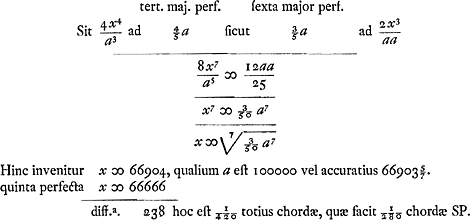
At ex priori systemate erat 1/320. Ergo hic perexigua differentia est, sed tamen quintae paulo adhuc minores. et quartae majores.
Porro fit LP sive 2x3/aa ∞ 59893 7/10 quae subducta a vera sextae majoris longitudine quae est 60000, relinquit tantum 105Ga naar voetnoot22), hoc est 1/1000 fere tantum totius chordae, quae fecit 1/563 chordae LP. at ex priori systemate erat 1/320, quantum nempe quintae longitudo veram superabat. Ergo hic jam sextae majores, simulque tertiae minores meliores fiunt quam in systemate praecedentiGa naar voetnoot23). Tertiae autem majores et sextae minores jam a veris recedunt tantundem praecise quantum tertiae majores et sextae minoresGa naar voetnoot24). fit enim MP ∞ 80142 quae debebat esse 80000, differentia est 142, quae etiam est 1/563 chordae MPGa naar voetnoot25).
Hic igitur tertiae majores et tertiae minores aequaliter à veris deficiunt, nempe accurate 1/7 commatisGa naar voetnoot26), quae differentia auribus nescio an percipi possit. Sextae vero majores et minores tantundem veras superant. Quintae deficiunt a veris duplo tanto nempe 2/7 commatisGa naar voetnoot27), accuratè, ac tantundem quartae veras superant.
§5. Ostendit autem experientia melius gratiusque auribus esse prius systema, necmirum cum in illo nulla consonantia tantum a vera recedat quam hîc. nam hîc jam sensibilius fit, etsi exiguo quintarum et quartarum vitium. deinde et tertiae majores, licet tantum 1/7 commatis deficiant, minus gratum sonum edunt quam cum perfectae sunt, ut in priori illo systemate, frequentissime autem occurrunt. Sed et facilius harum adjumento chordae omnes clavicymbali val fistulae organi ad suum quaeque tonum componuntur. Omnino igitur priori systemate uti praestat.
Modus autem quo secundùm illud chordae in ordinem rediguntur sive accordandi ut vocant clavecymbali vel organi est isteGa naar voetnoot28). Primo fiat
VM tertia major perfecta. et deinde MM2, diapason perfecta ut omnes.
Quo autem certius accipi possit 3a major perfecta, fiat primum diapason VV2. deinde inter has S quod sonet 5 tam perfectam ad V: et 4tam ad V2. tunc inter V et S ponatur M utrique perfectè consonans, alteri per 3am majorem, alteri per minorem. Postea relicto M perfecto, parum remittatur S, ut sit
VS quinta exiguo minor vera.
SR2 quinta similis. et R2R diapason.
RL quinta similis. Si jam LM2 inveniatur esse quinta prioribus similis recte se habent
hactenus omnia, sin minus tres tantum illae S, R2, L corrigendae sunt, usquedum LM2 inveniatur, ut dictum est, quinta deficiens similis. Hinc reliquae per tertias majores perfectas deducuntur LF, SC,LV2♯, MS♯, RF♯, R2L♯; SM♭. Ita omnes habentur, unde reliquae per diapafon sursum ac deorsumGa naar voetnoot29).
Si ad semitonos S♯, V♯, M♭ alij semitoni superaddantur, poterit quisque tonus diatonicus infra ac supra habere consonantes secundum omnes consonantias. Ponendo V2S* tertiam majorem perfectam, ut et CR2*, FV*. fit ergo S* ∞ a5/8x4. R2* ∞ 16x9/a8, V* ∞ a6/8x5Ga naar voetnoot30).
Falsae quartae sive tritoni similesGa naar voetnoot31) sunt VF♯, RS♯, M♭L,FC,SV2♯C♭ M2. suntque paulo minores quam 7 ad 5, nempe 1/571Ga naar voetnoot32), hoc est minus quam 1/7 commatis. ac fortasse et haec consonantia censenda est. quintae falsae sive quintae minores similes sunt V♯S, M♭. F♯V2,S♯R, LR2♯, CF2; tantundem superant rationem 10 ad 7. vocentur hae tritoni majoresGa naar voetnoot33).
- voetnoot1)
- Portefeuille ‘Musica’, f. 7-8. Huygens intitule cette Pièce ‘Divisio Monochordi’.
- voetnoot3)
- Ici as est déterminé comme le ton formant une tierce avec le ton plus haut
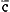 .
.
- voetnoot2)
- Partant d'une corde de longueur a Huygens calcule les longueurs des cordes dont les tons forment avec le ton fondamental les intervalles du système pythagoricien. Il pose x pour la longueur de la corde correspondant à la quinte du ton fondamental, de sorte que le rapport x/a de l'intervalle fondamental de la construction pythagoricienne reste momentanément indéterminé.
Soit en notations modernes V (c) le ton de la corde fondamentale. Comme nous l'avons dit, Huygens prend pour le ton S (g) une corde de longueur x. Pour R2 (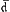 ) il en déduit x2/a en montant d'une quinte (diapente), et pour R (d) 2 x2/a en descendant ensuite d'une octave (diapason). De la même manière L (a) et M2 (e) se dérivent de ce dernier ton en montant chaque fois d'une quinte, ensuite M (e) en descendant d'une octave. La quinte de M donne C (b). Puisque l'intervalle SV2 (g-
) il en déduit x2/a en montant d'une quinte (diapente), et pour R (d) 2 x2/a en descendant ensuite d'une octave (diapason). De la même manière L (a) et M2 (e) se dérivent de ce dernier ton en montant chaque fois d'une quinte, ensuite M (e) en descendant d'une octave. La quinte de M donne C (b). Puisque l'intervalle SV2 (g-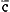 ) est une quarte, le rapport des longueurs des cordes correspondantes est apparemment a/2x. Ensuite F (f) se tire de V (c); en montant de nouveau d'une quarte on trouve ♭ (bes). L'intervalle VM (c-e) est une tierce majeure pythagoricienne, à laquelle correspond le rapport des longueurs 4(x/a)4. Le même intervalle sépare R (d) de F♯ (fis), M (e) de S♯ (gis), L (a) de V2♯ (cis), d'où suit V♯ (cis). ♭ (bes) est calculé une deuxième fois en descendant d'une tierce majeure à partir de R2 (
) est une quarte, le rapport des longueurs des cordes correspondantes est apparemment a/2x. Ensuite F (f) se tire de V (c); en montant de nouveau d'une quarte on trouve ♭ (bes). L'intervalle VM (c-e) est une tierce majeure pythagoricienne, à laquelle correspond le rapport des longueurs 4(x/a)4. Le même intervalle sépare R (d) de F♯ (fis), M (e) de S♯ (gis), L (a) de V2♯ (cis), d'où suit V♯ (cis). ♭ (bes) est calculé une deuxième fois en descendant d'une tierce majeure à partir de R2 (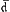 ). M (es) provient de S (g) de la méme manière.
). M (es) provient de S (g) de la méme manière.
Tous les tons du système ont donc été déduits du ton fondamental par des sauts de quintes et de tierces avec réductions d'octaves; la relation de chacun d'eux avec la tonique est donnée dans le tableau suivant, où T indique un saut de tierce, Q un saut de quinte et O un saut d'octave, chaque symbole placé dans le numérateur désignant une ascension, dans le dénominateur, une descente.V V♯ R R♯(M♭) M F F♯ S S♯ L 3QT/2O 2Q/O Q/T 4Q/2O = T O/Q 2QT/O Q 2T 3Q/O C♭ C V2 V2♯ R2 R2♯(M2♭) M2 F2 2O/2Q = 2Q/T TQ O 3QT/O 2Q QO/T 4Q/O 2O/Q
- voetnoot4)
- Nous remarquons que Huygens, pour obtenir une gamme chromatique pythagoricienne juste de 12 intervalles, emprunte les tons destinés à compléter la gamme diatonique en partie (savoir cis, fis et gis) à la partie ascendante, en partie (savoir es et bes) à la partie descendante de la série des quintes. En poursuivant la marche ascensionnelle, il aurait trouvé 32x9/a8 pour dis et 32x10/a9 pour ais. Dans l'octave qui commence par V2, M♭2 a été remplacé par R♯ (lisez R2♯).
- voetnoot5)
- Appelé plus haut ♭ [bes].
- voetnoot6)
- Il faut entendre S♯M♭2; permutation enharmonique de
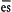 et de
et de 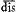 .
.
- voetnoot7)
- Savoir M♭S♯, de nouveau en vertu d'une substitution enharmonique.
- voetnoot8)
- Ou plutôt M♭S.
- voetnoot9)
- Savoir V♯F, F♯♭, S♯V2, CM♭2 (chez Huygens CR♯2).
- voetnoot10)
- Savoir M♭F♯, FS♯, ♭V2♯.
- voetnoot11)
- Lisez M♭V2.
- voetnoot12)
- Savoir V♯♭, F♯M2♭, S♯F2.
- voetnoot13)
- Savoir VS♯, M♭C, FV2♯ et ♭F2♯.
- voetnoot14)
- Il appert donc ici qu'on ne peut faire accorder la construction de la gamme par sauts de quintes et réductions d'octaves avec les rapports des intervalles consonants suivant le tempérament harmonique naturel.
- voetnoot15)
- C'est à dire pour obtenir la vraie sixte majeure, la corde LP devrait être allongée de 1/80 (ou bien la corde VP raccourcie de 1/81).
- voetnoot16)
- Le ton entier VR (c-d) acquiert la valeur 8:9. Pour monter d'un ton entier, il faut donc diminuer la longueur de la corde de 1/9, c.à.d. 9 fois d'avantage que pour passer de la vraie sixte majeure à celle figurant dans la construction pythagoricienne. C'est ce qu'on peut exprimer en disant qu'un comma (savoir un comma syntonique) est environ 1/9 d'un ton. Il s'agit en somme de l'approximation (80/81)9 = (1 - 1/81)9 ≈ 1 - 1/9.
- voetnoot17)
- En effet, 208/100000 ≈ 1/480.
- voetnoot18)
- La longueur de la corde devient pour la tierce mineure 5¾/4 a = 3/2.5¼ · 5/6 a. Son intervalle avec la véritable tierce mineure est donc égal à celui de la quinte tempérée avec la quinte véritable: en effet, ∜1/5 a4 = 3/2.5¼ · 2/3 a.
- voetnoot19)
- En effet, 1/480 a = 1/320 · 2/3 a.
- voetnoot20)
- D'après l'hypothese initiale pour la sixte; pour la quarte on trouve a2/2x = a.5¼/2 = 2.5¼/3 · 3/4 a.
- voetnoot21)
- Comme plus haut, ceci résulte d'une substitution enharmonique. On trouve les mêmes intervalles que dans les cas énumérés, lorsqu'on prend 32x9/a8 pour R♯ et qu'on remplace C (bes) par ais (32x10/a9).
- voetnoot22)
- Lisez 106.
- voetnoot23)
- Le système trouvé dans ce § est connu sous le nom de tempérament de Zarlino; voyez l'Avertissement (p. 46).
- voetnoot24)
- Lisez: quantum sextae majores et tertiae minores.
- voetnoot25)
- Ceci résulte de la condition imposée aux tierces et sixtes majeures. La validité de la thèse pour les tierces et sixtes mineures résulte de ce que la condition
a4/4x3 : 5/6 a = 5/8 a : a5/8x4
(voyez la note 3 de la p. 51) conduit elle aussi précisément à la valeur de x dont il vient d'être question dans le texte.
- voetnoot26)
- On trouve pour la tierce majeure la longueur de corde 4(3/50)4/7a, c.à.d. 5(3/50)4/7 · 4/5a. Lorsque l'intervalle avec la tierce majeure naturelle est septuplé, on obtient 57(3/50)4 = 81/80, c.à.d. le comma syntonique.
- voetnoot27)
- En effet, la longueur de corde de la quinte devient
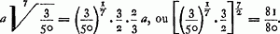
- voetnoot28)
- Le Manuscrit 13 contient (f. 52) une note sur le même sujet sous le titre: Chordas Clavicymbali in ordinem redigemus hoc modo. Cette Pièce se distingue de notre texte par le remplacement de M♭ par R♯ et par quelques changements et compléments que nous indiquons dans les notes qui suivent.
- voetnoot29)
- Manuscrit 13: nec nisi per octavos sursum ac deorsum procedere est opus.
- voetnoot30)
- Cet alinéa fait défaut dans le Manuscrit 13.
- voetnoot31)
- Dans le Manuscrit 13 seulement: Tritoni minores similes.
- voetnoot32)
- Pour x = a ∜ 1/5 on obtient F♯ = 8x6/a5 = 8(1/5)3/2 · a. Pour a = 100000 ceci devient 71554, ce qui surpasse 5/7. 100000 ou 71429 de 125, c.à.d. de 1/571. 71429.
- voetnoot33)
- Dans le Manuscrit 13 la phrase ‘Quintae falsae... tritoni majores’ à été remplacée par Horum complementa sive tritoni majores similes sunt F♯, V2 : S♯, R2 : L,R2♯ : C,F2 : V♯, S : M,L♯ : quae tantundem superant rationem 10 ad 7. ideoque omnino majores sunt tritonis minoribus cum jam ratio 10 ad 7 sit major quam 7 ad 5. Fortasse autem et horum uterque consonantijs accensendus est.

