Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695
(1937)–Christiaan Huygens–Chap. III. De la refraction.De mesme que les effets de la Reflexion ont esté expliquez par les ondes de la lumiere reflechies à la surface des corps polis, nous expliquerons la transparence, & les phenomenes de la refraction, par les ondes qui s'étendent au dedans & au travers des corps diaphanes, tant solides, comme le verre, que liquides, comme l'eau les huiles &c. Mais afin qu'il ne paroisse pas estrange de supposer ce passage des ondes au dedans de ces corps, je feray voir auparavant qu'on peut le concevoir possible en plus d'une maniere. | |
[pagina 481]
| |
Premierement donc quand la matiere etherée ne penetreroit | aucunement les corpsGa naar margenoot+ transparens, leurs particules mesmes se pourroient communiquer successivement le mouvement des ondes, de mesme que celles de l'Ether; estant supposeés, comme celles cy, de nature à faire ressort. Et cela est aisé à concevoir pour ce qui est de l'eau, & des autres liqueurs transparentes, comme estant composeés de particules detachées. Mais il peut sembler plus difficile à l'egard du verre, & des autres corps transparens & durs; par ce que leur solidité ne semble pas permettre qu'ils puissent recevoir du mouvement que dans toute leur masse à la fois. Ce qui pourtant n'est pas necessaire, parce que cette solidité n'est pas telle qu'elle nous paroit; estant probable que ces corps sont plustost composez de particules, qui ne sont que posées les unes auprés des autres, & retenues ensemble par quelque pression de dehors d'une autre matiere, & par l'irregularité des figures. Car premierement leur rareté paroit par la facilité avec laquelle y passe la matiere des tourbillons de l'aimant, & celle qui cause la pesanteur. De plus l'on ne peut pas dire que ces corps soient d'un tissu semblable à celuy d'une éponge, ou du pain leger, parce que la chaleur du feu les fait couler, & change par là la situation des particules entre elles. Il reste donc que ce soient, comme il a esté dit, des assemblages de particules qui se touchent, sans composer un solide continu. ce qui estant ainsi, le mouvement que ces particules reçoivent pour continuer les ondes de lumiere, ne faisant que se communiquer des unes aux autres; sans qu'elles sortent pour cela de leur place, ou qu'elles se dérangent entr'elles; il peut fort bien faire son effet sans prejudicier en rien à la solidité du composé qui nous paroit. Par la pression de dehors, dont j'ay parlé, il ne faut pas entendre celle de l'air, qui ne seroit pas suffisante, mais une autre d'une matiere plus subtile, laquelle pression se manifeste dans cette experience que le hazard m'a fait rencontrer il y a long|temps;Ga naar margenoot+ sçavoir de l'eau purgée d'air, qui demeure suspenduë dans un tuyau de verre ouvert par le bout d'enbas, non-obstant que l'air soit osté du vaisseau où ce tuyau est enferméGa naar voetnoot1). L'on peut donc de cette maniere concevoir la transparence sans qu'il soit besoin que la matiere etherée, qui sert à la lumiere, y passe, ny qu'elle trouve des pores pour s'y insinuer. Mais la verité est que cette matiere non seulement y passe, mais mesme avec grande facilité; dequoy l'experience de Torricelli, dessus alleguée, est deja une preuve. Par ce que le vif argent & l'eau, quitant la partie haute du tuyau de verre, il paroit qu'elle est remplie aussi-tost de la matiere etherée, puisque la lumiere y passe. Mais voicy un autre argument qui prouve cette penetrabilité aiseé, non seulement dans les corps transparens, mais aussi dans tous les autres. | |
[pagina 482]
| |
Lorsque la lumiere passe à travers d'une sphere creuse de verre, fermée de toutes parts, il est constant qu'elle est pleine de la matiere etherée, autant que les espaces au dehors de la sphere. Et cette matiere etherée, comme il a este monstré cy devant, consiste en des particules qui se touchent prez à prez. Si elle estoit donc tellement enfermée dans la sphere qu'elle ne pûst sortir par les pores du verre, elle seroit obligée de suivre le mouvement de la sphere lorsqu'on la fait changer de place: & il faudroit par consequent la mesme force à peu pres pour imprimer une certaine vitesse à cette sphere, lorsqu'elle seroit posée sur un plan horizontal, que si elle estoit pleine d'eau ou peutestre de vif argent: parce que tout corps resiste à la vitesse du mouvement, qu'on veut luy donner, selon la quantité de la matiere qu'il contient, & qui doit suivre ce mouvement. Mais on trouve au contraire que la sphere ne resiste à l'impression du mouvement que selon la quantité de la matiere du verre dont elle est faite: donc il faut que la matiere etherée, qui est dedans, ne soit point enfermée, mais qu'elle couleGa naar margenoot+ à travers avec tres grande liberté. | Nous ferons voir cy apres que la mesme penetrabilité se conclud aussi, par ce moyen, en ce qui est des corps opaques. La seconde maniere donc d'expliquer la transparence, & qui paroit plus vrai-semblable, c'est en disant que les ondes de lumiere se continuent dans la matiere etherée, qui occupe continuellement les interstices, ou pores des corps transparens. Car puisqu'elle y passe continuellement, & avec facilité, il s'ensuit qu'ils s'en trouvent tousjours remplis. Et l'on peut mesme demonstrer que ces interstices occupent beaucoup plus d'espace que les particules coherentes qui constituent les corps. Car s'il est vray ce que nous venons de dire, qu'il faut de la force pour imprimer certaine vitesse horizontale aux corps, à proportion qu'ils contiennent de la matiere coherente; & si la proportion de cette force suit la raison des pesanteurs, ce qui se confirme par l'experience; donc la quantité de la matiere constituante des corps suit aussi la proportion des pefanteurs. Or nous voyons que l'eau ne pese que la quatorzieme partie autant qu'une portion egale de vif argent: donc la matiere de l'eau n'occupe pas la quatorzieme partie de l'espace que tient sa masseGa naar voetnoot1). Mesme elle en doit occuper bien moins, puisque le vif argent est moins pesant que l'or; & que la matiere de l'or est fort peu dense: comme il s'ensuit de ce que la matiere des tourbillons de l'aimant, & de celle qui cause la pesanteur y passent tres librement. Mais on peut objecter icy que, si le corps de l'eau est d'une si grande rareté, & que ses particules occupent une si petite portion de l'espace de son étendue apparente, il est bien étrange comment elle resiste pourtant si sort à la Compression, sans se laisser condenser par aucune force qu'on ait essaié jusqu'ici d'y employer; conservant mesme toute sa liquidité, pendant qu'elle souffre cette pression. Ga naar margenoot+ Ce n'est pas icy une petite difficulté. Laquelle pourtant on | peut resoudre en disant que le mouvement tres violent & rapide de la matiere subtile qui rend l'eau liquide, | |
[pagina 483]
| |
en ébranlant les particules dont elle est composée, maintient cette liquidité malgré la pression que jusqu'icy on se foit avisé d'y appliquer. La rareté des corps transparens estant donc telle que nous avons dit, l'on conçoit aisement que les ondes puissent estre continuées dans la matiere etherée qui emplit les interstices des particules. Et de plus l'on peut croire que le progrez de ces ondes doit estre un peu plus lent au dedans des corps, à raison des petits detours que causent les mesmes particules. Dans laquelle differente vitesse de la lumiere, je feray voir que consiste la cause de la refraction. J indiqueray auparavant la troisiéme & derniere maniere dont on peut concevoir la transparence, qui est en supposant que le mouvement des ondes de lumiere se transmet indifferemment & dans les particules de la matiere etherée, qui occupent les interstices des corps, & dans les particules qui les composent, en sorte que ce mouvement passe des unes aux autres. L'on verra cy apres que cette hypothese sert beaucoup à expliquer la refraction double de certains corps diaphanes. Que si l'on objecte que les particules de l'ether estant plus petites que celles des corps transparens, puis qu'elles passent par leurs intervalles, il s'ensuivroit qu'elles ne leur pourroient communiquer que peu de leur mouvement; l'on peut respondre, que les particules des corps sont encore composées d'autres particules plus petites; & qu'ainsi ce seront ces particules secondes qui recevront le mouvement de celles de l'ether. Au reste, si celles des corps transparents ont leur ressort un peu moins prompt que n'est celuy des particules etherées, ce que rien n'empesche de supposer, il s'ensuivra derechef que le progrez des ondes de lumiere sera plus lent au dedans de ce corps, qu'elle n'est au dehors dans la matiere etherée. C'est là tout ce que j'ay trouvé de plus vrai-semblable pour la maniere dont les ondesGa naar margenoot+ de la lumiere passent à travers les corps transparens. A quoy il faut encore adjouter en quoy ces corps different de ceux qui sont opaques; & d'autant plus qu'il peut sembler, à cause de la facile penetration des corps par la matiere etherée, dont il a este parlé, qu'il n'y auroit point de corps qui ne fût transparent. Car par la mesme raison de la sphere creuse, que j'ay emploiée pour prouver le peu de densité du verre, & sa penetrabilité aiseé à la matiere etherée, l'on peut aussi prouver que la mesme penetrabilité conuient aux metaux & à toute autre sorte de corps. Car cette sphere estant d'argent par exemple, il est certain qu'elle contient de la matiere etherée qui sert à la lumiere, puisque cette matiere y estoit aussi bien que l'air, lorsqu'on bouchoit l'ouverture de la sphere. Cependant estant fermée, & poseé sur un plan horizontal, elle ne resiste au mouvement qu'on luy veut donner que suivant la quantité de l'argent dont elle est faite. de sorte qu'il en faut conclurre, comme dessus, que la matiere étherée, qui est enfermée ne suit point le mouvement de la sphere; & que partant l'argent, aussi bien que le verre, est tres facilement penetré par cette matiere. Il s'en trouve donc continuellement & en quantité entre les particules de l'argent & de tous les autres corps opaques; & puis qu'elle sert à la propagation de la lumiere, il semble | |
[pagina 484]
| |
que ces corps devroient aussi estre transparens, comme le verre; ce qui pourtant n'est point. D'où dira-t-on donc que vient leur opacité? est ce que les particules qui les composent sont molles, c'est-à-dire que ces particules, estant composées d'autres moindres, sont capables de changer de figure en recevant l'impression des particules etherées, des quelles par là elles amortissent le mouvement, & empeschent ainsi la continuation des ondes de lumiere? Cela ne se peut: car si les particules des metaux sont molles,Ga naar margenoot+ comment | est ce que l'argent poli, & le mercure reflechissent si fortement la lumiere?! Ce que je trouve de plus vrai-semblable en cecy, c'est de dire que les corps des metaux, qui sont presque les seuls veritablement opaques, parmi leurs particules dures en ont de molles entremeslées; de sorte que les unes servent à causer la reflexion, & les autres à empescher la transparence; au lieu que les corps transparens ne contiennent que des particules dures, qui ont la faculté de faire ressort, & servent ensemble avec celles de la matiere etherée, ainsi qu'il a esté dit, à la propagation des ondes de la lumiere. Passons maintenant à l'explication des effects de la Refraction; en supposant, comme nous avons fait, le passage des ondes de la lumiere à travers les corps transparens, & la diminution de vitesse que ces mesmes ondes y souffrent. La principale proprieté de la Refraction est, qu'un rayon de lumiere, comme AB [Fig. 183], estant dans l'air, & tombant obliquement sur la surface polie d'un corps transparent comme FG, se rompt au point d'incidence B, en sorte qu'avec la droite DBE, qui coupe la surface perpendiculairement, il fait un angle CBE moindre que ABD, qu'il faisoit avec la mesme perpendiculaire estant dans l'air. Et la mesure de ces angles se trouve en décrivant un cercle du point B, qui coupe les rayons AB, BC. Car les perpendiculaires AD, CE menées des points d'intersection sur la droite DE, lesquelles on appelle les Sinus des angles ABD, CBE, ont entre elles une certaine raison, qui est tousjours la mesme dans toutes les inclinaisons du rayon incident, pourGa naar margenoot+ ce qui est d'un certain corps transparent. Estant dans le verre fort | prés comme de 3 à 2, & dans l'eau fort prés comme de 4 à 3; & ainsi differente dans d'autres corps diaphanes. Une autre proprieté, pareille à celle-cy, est que les refractions sont reciproques entre les rayons entrans dans un corps transparent, & ceux qui en sortent. C'est-à-dire que si le rayon AB en entrant dans le corps transparent se rompt en BC, aussi CB, estant pris pour un rayon au dedans de ce corps, se rompra, en sortant, en BA. Pour expliquer donc les raisons de ces phenomenes suivant nos principes, soit la droite AB [Fig. 184], qui represente une surface plane, terminant les corps transparens qui sont vers C & vers N. Quand je dis plane, cela ne signifie pas d'une egalité parfaite, mais telle qu'elle a esté entendue en traitant de la reflexion, & par la mesme raison. Que la ligne AC represente une partie d'onde de lumiere, dont le centre soit supposé si loin, que cette partie puisse estre considerée comme une ligne droite. L'endroit C donc, de l'onde AC, dans un certain espace de temps sera avancé jusqu'au plan AB suivant la droite CB, que l'on doit imaginer qu'elle vient du centre lumineux, | |
[pagina 485]
| |
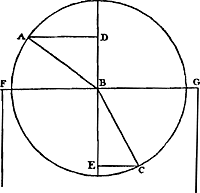 [Fig. 183.]
 [Fig. 184.]
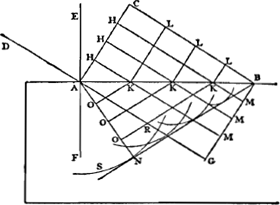
& qui par consequent coupera AC à angles droits. Or dans le mesme temps l'endroit A seroit venu en G par la droite AG, egale & parallele à CB; & toute la partie d'onde AC seroit en GB, si la matiere du corps transparent transmettoit le mouvement de l'onde | aussi vîte que celle de l'Ether. Mais supposons qu'elle transmetteGa naar margenoot+ ce mouvement moins vîte, par exemple, d'un tiers. Il se sera donc repandu du mouvement depuis le point A, dans la matiere du corps transparent, par une etendue egale aux deux tiers de CB, faisant son onde spherique particuliere, suivant ce qui a esté dit cy devant; laquelle onde est donc representeé par la circonference SNR, dont le centre est A, & le demi diametre egal aux ⅔ de CB. Que si l'on considere ensuite les autres endroits H de l'onde AC, il paroit que dans le mesme temps que l'endroit C est venu en B, ils ne seront pas seulement arrivez à la surface AB, par des droites HK paralleles à CB, mais que de plus ils auront engendré, des centres K, des ondes particulieres dans le diaphane, representées icy par des circonferences dont les demi-diametres sont egaux aux ⅔ des lignes KM, c'est à dire aux ⅔ des continuations de HK jusqu' à la droite BG; car ces demi-diametres auroient esté agaux aux KM entieres, si les deux diaphanes estoient de mesme penetrabilité. Or toutes ces circonferences ont pour tangente commune la ligne droite BN: sçavoir la mesme qui du point B est faite tangente de la circonference SNR, que nous avons considerée la premiere. Car il est aisé de voir que toutes les autres circonferences vont toucher à la mesme BN, depuis B jusqu'au point de contact N, qui est le mesme ou tombe AN perpendiculaire sur BN. C'est donc BN, qui est comme formée par de petits arcs de ces circonferences, qui termine le mouvement que l'onde AC a communiqué dans le corps transparent, & ou ce mouvement se trouve en beaucoup plus grande quantité que par tout ailleurs. Et pour cela cette ligne, suivant ce qui a esté dit plus d'une fois, est la propagation de l'onde AC dans le moment que son endroit C est arrivé en B. Car il n'y a point d'autre ligne au dessous du plan AB qui, comme BN, soit tangente commune de | |
[pagina 486]
| |
 [Fig. 184.]
 [Fig. 185.]
Ga naar margenoot+ toutes lesdites ondes particulieres. Que si l'on veut sça | voir comment l'onde AC est venue successivement en BN, il ne faut que dans la mesme figure tirer les droites KO paralleles à BN, & toutes les KL paralleles à AC. Ainsi l'on verra que l'onde CA, de droite est devenue brisée dans toutes les LKO successivement, & qu'elle est redevenue droite en BN. Ce qui estant evident par ce qui a desja esté monstré, il n'est pas besoin de l'eclaircir davantage. Or, dans la mesme figure, si on mene EAF [Fig. 184], qui coupe le plan AB à angles droits au point A, & que AD soit perpendiculaire à l'onde AC, ce sera DA qui marquera le rayon de lumiere incident, & AN, qui estoit perpendiculaire à BN, le rayon rompu: puisque les rayons ne sont autre chose que les lignes droites suivant lesquelles les parties des ondes s'estendent. D'où il est aisé de reconnoitre cette principale proprieté des refractions, sçavoir que le Sinus de l'angle DAE, a tousjours une mesme raison au Sinus de l'angle NAF, quelle que soit l'inclinaison du rayon DA: & que cette raison est la mesme que celle de la vitesse des ondes dans le diaphane qui est vers AE, à leur vitesse dans le diaphane vers AF. Car considerant AB comme rayon d'un cercle, le Sinus de l'angle BAC est BC, & le Sinus de l'angle ABN est AN. Mais l'angle BAC est egal à DAE; puisque chacun d'eux, adjouté à CAE, fait un angle droit. Et l'angle ABN est egal à NAF;Ga naar margenoot+ puisque chacun d'eux avec BAN fait | un angle droit. Donc le Sinus de l'angle DAE est aussi au Sinus de NAF comme BC à AN. Mais la raison de BC à AN estoit la mesme que celle des vitesses de la lumiere dans la matiere qui est vers AE & dans celle qui est vers AF; donc aussi le Sinus de l'angle DAE au Sinus de l'angle NAF sera comme lesdites vitesses de la lumiere. Pour voir ensuite quelle doit estre la refraction, lorsque les ondes de lumiere passent dans un corps, où le mouvement s'étend plus vîte que dans celuy d'ou ils sortent, | |
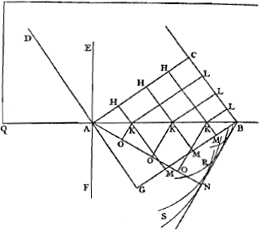
[pagina 487]
| |
(posons derechef selon la raison de 3 à 2) il ne faut que repeter toute la mesme construction & demonstration que nous venons de mettre; en substituant seulement partout 3/2 au lieu de ⅔. Et l'on trouvera par le mesme raisonnement, dans cette autre figure, que lorsque l'endroit C [Fig. 185] de l'onde AC sera parvenu jusqu'a la surface AB en B, toute la partie d'onde AC sera avancée en BN, en sorte que BC perpendiculaire sur AC soit à AN perpendiculaire sur BN comme 2 à 3. Et que cette mesme raison de 2 à 3 sera enfin entre le Sinus de l'angle EAD, & le Sinus de l'angle FAN. D'icy l'on voit la reciprocation des refractions du rayon entrant & sortant d'un mesme diaphane: sçavoir que si NA tombant sur la surface exterieure AB, se rompt en AD, aussi le rayon DA se rompra, en sortant du diaphane, en AN. L'on voit aussi la raison d'un accident notable qui arrive dans cette refraction; quiGa naar margenoot+ est que depuis une certaine obliquité du rayon incident DA, il commence à ne point pouvoir penetrer dans l'autre diaphane. Car si l'angle DAQ ou CBA est tel que dans le triangle ACB, CB soit egal aux ⅔ de AB, ou plus grande, alors AN ne peut pas faire un côté du triangle ANB parce qu'elle devient egale à AB, ou plus grande: de sorte que la partie d'onde BN ne se trouve nulle part, ni par consequent AN, qui luy devoit estre perpendiculaire. Et ainsi le rayon incident DA ne perce point alors la surface AB. Quand la raison des vitesses des ondes est de deux à trois, comme dans nostre exemple, qui est celle qui convient au verre & à l'air, l'angle DAQ doit estre plus grand que de 48. deg. 11. min. afin que le rayon DA puisse passer en se rompant. Et quand la raison de ces vitesses est de 3 à 4, comme elle est à fort peu prés dans l'eau & l'air, cet angle DAQ doit exceder 41. degrez 24. minutes. Et cela s'accorde parfaitement avec l'experience. Mais on pourroit demander icy, puisque la rencontre de l'onde AC contre la surface AB doit produire du mouvement dans la matiere qui est de l'autre costé, pourquoy il n'y passe point de lumiere. A quoy la réponse est aisée si l'on se souvient de ce qui a esté dit cidevant. Car bien qu'il s'engendre une infinité d'ondes particulieres dans la matiere qui est de l'autre costé de AB, il n'arrive point à ces ondes d'avoir une ligne tangente commune (soit droite ou courbe) en un mesme instant; & ainsi il n'y a point de ligne qui termine la propagation de l'onde AC au delà du plan AB, ni où le mouvement soit ramassé en assez grande quantité pour produire de la lumiere. Et l'on verra aisement la vérité de cecy, sçavoir que CB estant plus grande que les ⅔ de AB, les ondes excitées au delà du plan AB n'auront point de commune tangente, si des centres K l'on de|crit alors des cercles, ayans les rayons egaux aux 3/2 des LBGa naar margenoot+ qui leur répondent. Car tous ces cercles seront enfermez les uns dans les autres, & passeront tous au dela du point B. Or il est à remarquer que, dés lors que l'angle DAQ est plus petit qu'il ne faut pour permettre que le rayon DA rompu puisse passer dans l'autre diaphane, l'on trouve que la reflexion interieure, qui se fait à la surface AB, s'augmente de beaucoup | |
[pagina 488]
| |
en clarté; comme il est aisé d'experimenter avec un prisme triangulaire: dequoy l'on peut rendre cette raison par nostre Theorie. Lorsque l'angle DAQ est encore assez grand pour faire que le rayon DA puisse passer, il est manifeste que la lumiere de la partie d'onde AC est ramassée dans une moindre estendue, lorsqu'elle est parvenue en BN. Il paroit aussi que l'onde BN devient d'autant plus petite que l'angle CBA ou DAQ est fait plus petit; jusqu'a ce qu'estant diminué jusqu'a la determination peu auparavant marquée, cette onde BN se ramasse toute comme dans un point. C'est à dire que quand l'endroit C de l'onde AC est alors arrivé en B, l'onde BN, qui est la propagation de AC, est toute reduite au mesme point B; de mesme que, quand l'endroit H estoit arrivé en K, la partie AH estoit toute reduite au mesme point K. Ce qui fait voir qu'a mesure que l'onde CA est venu rencontrer la surface AB, il s'est trouvé grande quantité de mouvement le long de cette surface; lequel mouvement se doit estre repandu aussi en dedans du corps transparent, & avoir renforcé de beaucoup les ondes particulieres, qui produisent la reflexion interieure contre la surface AB, suivant les loix de la reflexion cy devant expliquées. Et parce qu'un peu de diminution à l'angle d'incidence DAQ, fait devenir l'onde BN, d'assez grande qu'elle estoit, à rien: (car cet angle estant dans le verre de 49. degrez 11. min. l'angle BAN est encore de 11. degrez 21. min, & le mesme angleGa naar margenoot+ DAQ estant diminué d'un degré seulement, l'angle BAN est re|duit à rien, & ainsi l'onde BN reduite à un point:) dela vient que la reflexion interieure d'obscure devient subitement claire, dés lors que l'angle d'incidence est tel qu'il ne donne plus passage à la refraction. Or pour ce qui est de la reflexion exterieureGa naar voetnoot1) ordinaire, c'est a dire qui arrive lors que l'angle d'incidence DAQ est encore assez grand pour faire que le rayon rompu puisse penetrer au dela de la superficie AB: cette reflexion se doit faire contre les particules de la matiere qui touche le corps transparent par dehors. Et c'est apparemment contre les particules de l'air & autres, meslées parmy la matiere etherée, & plus grossiere qu'elle. Comme d'autre costé la reflexion exterieure de ces corps se fait contre les particules qui les composent, & qui sont aussi plus grosses que celles de la matiere étherée, puisque celle-cy coule dans leurs intervalles. Il est vray qu'il reste en cecy quelque difficulté dans les experiences où cette reflexion interieure se fait sans que les particules de l'air y puissent contribuer, comme dans des vaisseaux ou tuyaux d'où l'air a esté tiréGa naar voetnoot2). L'experience au reste nous apprend que ces deux reflexions sont à peu pres d'egale force, & que dans les differens corps transparens elles en ont d'autant plus que la refraction de ces corps est plus grande. Ainsi l'on voit manifestement que la reflexion du verre est plus forte que celle de l'eau, & celle du diamant plus forte que celle du verre. | |
[pagina 489]
| |
Je finiray cette theorie de la refraction en demonstrant une proposition remarquable qui en depend; sçavoir qu'un rayon de lumiere pour aller d'un point à un autre, quand ces points sont dans des diaphanes differens, se rompt en sorte à la surface plane qui joint ces deux milieux, qu'il employe le moindre temps possible; tout de mesme qu'il arrive dans la reflexion contre une surface plane. Mr. Fermat a proposé le premier cette proprieté des refractionsGa naar voetnoot3), tenant comme nous, & dire|ctement contre l'opinionGa naar margenoot+ de Mr. Des Cartes, que la lumiere passe plus lentement à travers le verre & l'eau qu'a travers l'air. Mais il supposoit outre cela la proportion constante des Sinus, que nous venons de prouver par ces seuls divers degrez de vitesse: ou bien, ce qui vaut autant, il supposoit outre ces diverses vitesses, que la lumiere employoit en ce passage le moindre temps possible, pour en conclurre la proportion constante des Sinus. Sa demonstration, qui se voit dans ses ouvrages imprimez & dans le livre des lettres de Mr. Des Cartes, est fort longue; c'est pourquoy je donne icy cette autre plus simple & plus facile. 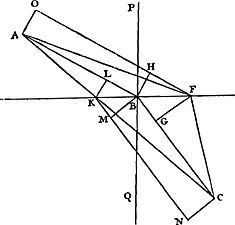 [Fig. 186.]
Soit la surface plane KF [Fig. 186]; le point A dans le diaphane que la lumiere traverse plus facilement, comme l'air; le point C dans un autre plus difficile à penetrer, comme l'eau; & qu'un rayon soit venu de A, par B en C, ayant este rompu en B suivant la loy peu auparavant demonstrée; c'est à dire qu'ayant mené PBQ, qui coupe le plan à angles droits, le sinus de l'angle ABP au sinus de l'angle CBQ ait la mesme raison que la vitesse de la lumiere dans le diaphane, où est A, à sa vitesse où est C. Il faut demonstrer que les temps du passage de la lumiere par AB & BC, pris ensemble, sont les plus courts qu'ils peuvent estre. Prenons qu'elle soit venue par d'autres lignes, & premierement par AF, FC, en sorte que le point de refraction F soit plus distant que B du point A, & soit AO, perpendiculaire sur | AB, FO parallele à AB; BH perpendiculaireGa naar margenoot+ sur FO, & FG sur BC. Puisque donc l'angle HBF est egal à PBA, & l'angle BFG egal a QBC; il s'ensuit que le sinus de l'angle HBF aura aussi au sinus de BFG la mesme raison que la vitesse de la lumiere dans le diaphane A, à sa vitesse dans le diaphane C. Mais ces sinus sont les droites HF, BG, en prenant BF pour demi-diametre d'un cercle. Donc ces lignes, HF, BG ont entre elles ladite raison des vitesses. Et partant le temps de la lumiere | |
[pagina 490]
| |
par HF, supposé que le rayon fut OF, seroit egal au temps par BG au dedans du diaphane C. Mais le temps par AB est egal au temps par OH; donc le temps par OF est egal au temps par AB, BG. Derechef le temps par FC est plus long que par GC, donc le temps par OFC sera plus long que par ABC. Mais AF est plus grande que OF, donc le temps par AFC excedera d'autant plus le temps par ABC. Prenons maintenant que le rayon soit venu de A en C par AK, KC; le point de refraction AK estant plus prés de A que n'est le point B; & soit CN perpendiculaire sur BC, KN parallele à BC: BM perpendiculaire sur KN, & KL sur BA. Icy BL & KM sont les sinus des angles BKL, KBM, c'est à dire des angles PBA, QBC; & partant elles sont entre elles comme la vitesse de la lumiere dans le diaphane A, à la vitesse dans le diaphane C. Donc le temps par LB est egal au temps par KM; & puis que le temps par BC est egal au temps par MN, le temps par LBC sera egal au temps par KMN. Mais le temps par AK est plus long que par AL: donc le temps par AKN est plus long que par ABC. Et KC estant plus longue que KN, le temps par AKC surpassera d'autant plus le temps par ABC. Ainsi il paroit que le temps par ABC est le plus court qu'il peut estre; ce qu'il falloit demonstrer. |
|

