Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

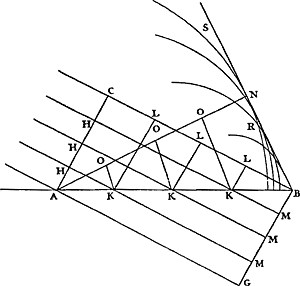
Chap. II. De la reflexion.

Ayant expliqué les effets des ondes de lumiere, qui s'étendent dans une matiere⁺ homogene, nous examinerons ensuite ce qui leur arrive en rencontrant d'autres corps. Nous ferons voir premierement comment par ces mesmes ondes s'explique la Reflexion de la lumiere, & pourquoy elle garde l'egalité des angles. Soit une surface plane & polie, de quelque metail, verre ou autre corps, AB, [Fig. 181] que d'abord je considereray comme parfaitement unie (me reservant à parler des inégalitez, dont elle ne peut estre exempte, à la fin de cette demonstration) & qu'une ligne AC, inclinée sur AB, represente une partie d'une onde de lumiere, dont le centre soit si loin que cette partie AC puisse estre considerée comme une ligne droite; parce que je considere tout cecy comme dans un seul plan, m'imaginant que le plan, ou est cette figure, coupe la sphere de l'onde par son centre, & le plan AB à angles droits; ce qu'il suffit d'avertir une fois pour toutes.

L'endroit C de l'onde AC, dans un certain espace de temps, sera avancé jusqu'au⁺ plan AB en B, suivant la droite CB, que l'on doit s'imaginer venir du centre lumineux, & qui par consequent est perpendiculaire à AC. Or dans ce mesme espace de

+ (p. 21).

+ (p. 22).

[p. 478]

[Fig. 181.]

temps, l'endroit A de la mesme onde, qui a esté empesché de communiquer son mouvement par de là le plan AB, ou du moins en partie, doit avoir continué son mouvement dans la matiere qui est au dessus de ce plan, & cela dans une étenduë egale à CB; faisant son onde spherique particuliere, suivant ce qui a esté dit cydessus. Laquelle onde est icy representeé par la circonference SNR, dont le centre est A, & le demidiametre AN égal à CB.

Que si l'on considere en suite les autres endroits H de l'onde AC, il paroit qu'ils ne seront pas seulement arrivez à la surface AB par les droites HK paralleles à CB, mais que de plus ils auront engendré, des centres K, des ondes spheriques particulieres dans le diaphane, representeés icy par des circonferences dont les demidiametres sont égaux aux KM, c'est à dire aux continuations des HK jusques à la droite BG parallele à AC.

Mais toutes ces circonferences ont pour tangente commune la ligne droite BN, sçavoir la mesme qui de B est faite tangente du premier de ces cercles, dont A estoit le centre, & AN le demidiametre égal à BC, comme il est aisé de voir.

C'est donc la ligne BN (comprise entre B & le point N, où tombe la perpendiculaire du point A), qui est comme formeé par toutes ces circonferences, & qui termine le mouvement qui s'est fait par la reflexion de l'onde AC; & c'est aussi où ce mouvement se trouve en beaucoup plus grande quantité que par tout ailleurs. C'est pourquoy, selon ce qui a esté expliqué, BN est la propagation de l'onde AC dans le moment que son endroit C est arrivé en B. Car il n'y a point d'autre ligne qui comme BN soit tangente commune de tous lesdits cercles, si ce n'est BG, au dessous du plan AB;⁺ laquelle BG seroit la propagation de l'onde si | le mouvement s'estoit pû étendre dans une matiere homogene à celle qui est au dessus du plan. Que si l'on veut voir comment l'onde AC est venue successivement en BN, l'on n'a qu'a tirer dans la mesme figure les droites KO paralleles à BN, & les droites KL paralleles à AC. Ainsi l'on verra que l'onde AC de droite est devenue briseé dans toutes les OKL successivement, & qu'elle est redevenue droite en NB.

Or il paroit d'icy que l'angle de reflexion se fait egal à l'angle d'incidence. Car les triangles ACB, BNA estant rectangles, & ayant le costé AB commun, & le costé

+ (p. 23).

[p. 479]

CB égal à NA, il s'ensuit que les angles opposez à ces costez seront égaux, & partant aussi les angles CBA, NAB. Mais comme CB, perpendiculaire à CA, marque la direction du rayon incident, ainsi AN, perpendiculaire à l'onde BN, marque la direction du rayon reflechi; donc ces rayons sont également inclinez sur le plan AB.

Mais en considerant la demonstration precedente, l'on pourroit dire qu'il est bien vray que BN est la tangente commune des ondes circulaires dans le plan de cette figure; mais que ces ondes, estant dans la verité spheriques, ont encore une infinité de pareilles tangentes, sçavoir toutes les lignes droites qui du point | B sont menées⁺ dans la surface du cone engendré par la droite BN autour de l'axe BA. Il reste donc à monstrer qu'il n'y a point de difficulté en cecy; & par la mesme raison l'on verra pourquoy tousjours le rayon incident & le reflechi sont dans un mesme plan perpendiculaire au reflechissant. Je dis donc que l'onde AC, n'estant considereé que comme une ligne, ne produit point de lumiere. Car un rayon visible de lumiere, quelque mince qu'il soit, a tousjours quelque épaisseur; & partant pour representer l'onde dont le progrez fait ce rayon, il faut au lieu d'une ligne AC, mettre une figure plane, comme dans la figure suivante le cercle HC, en supposant, comme on a fait, le point lumineux infiniment éloigné. Or il est aisé de voir, ensuite de la precedente demonstration, que chaque petit endroit de cette onde HC, estant parvenu jusqu'au plan AB, & engendrant de là chacun son onde particuliere; cellescy auront toutes, lorsque C sera arrivé en B, un commun plan qui les touchera, sçavoir un cercle BN pareil à CH, & qui sera coupé par le millieu, & à angles droits, par le mesme plan qui coupe ainsi le cercle CH & l'ellipse AB [Fig. 182].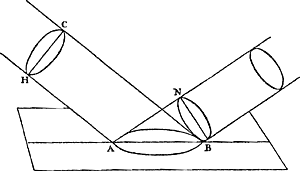

[Fig. 182.]

L'on voit aussi que les dites spheres des ondes particulieres ne peuvent point avoir d'autre commun plan touchant que le cer|cle BN; sorte que ce sera ce plan ou il⁺ y aura beaucoup plus de mouvement reflechy que par tout ailleurs, & qui pour cela portera la lumiere continuée de l'onde CH.

J'ay dit aussi dans la demonstration precedente, que le mouvement de l'endroit A de l'onde incidente ne s'est pû communiquer au de là du plan AB, ou du moins pas entierement. Où il faut remarquer que, quoyque le mouvement de la matiere etherée se communiquast en partie à celle du corps reflechissant, cela ne peut alterer

+ (p. 24).

+ (p. 25).

[p. 480]

en rien la vitesse du progrez des ondes, duquel depend l'angle de reflexion. Car une legere percussion doit engendrer des ondes aussi vîtes qu'une tres forte, dans une mesme matiere. Ce qui vient de la proprieté des corps qui font ressort, de laquelle nous avons encore parlé cy dessus; sçavoir que peu ou beaucoup pressez ils se restituent en des temps égaux. Partant dans toute reflexion de la lumiere, contre quelque corps que ce soit, les angles de reflexion & d'incidence doivent estre égaux; non-obstant que ce corps fust de telle nature qu'il ostast une partie du mouvement qui fait la lumiere incidente. Et l'experience monstre qu'en effet il n'y a aucun corps poli dont la reflexion ne suive cette regle.

Mais ce qu'il faut sur tout remarquer dans nostre demonstration, c'est qu'elle ne demande pas que la surface reflechissante soit considerée comme un plan uni; ainsi qu'ont supposé tous ceux qui ont tasché d'expliquer les effets de la reflexion; mais seulement d'une egalité telle que peuvent composer les particules de la matiere du corps reflechissant, mises les unes aupres des autres; lesquelles particules sont plus grandes que celles de la matiere etherée, comme il paroitra par ce que nous dirons en traitant de la transparence & de l'opacité des corps. Car la surface consistant ainsi en des particules mises ensemble, & les particules etherées estant par dessus, & plus⁺ petites, il est evident qu'on ne sçauroit demonstrer l'egalité des angles d'incidence, | & de reflexion par la ressemblance de ce qui arrive à une balle poussée contre un mur, de laquelle on s'est tousjours servi. Au lieu que dans nostre maniere la chose s'explique sans difficulté. Car la petitesse des particules du vif argent, par exemple, estant telle qu'il en faut concevoir des millions dans la moindre surface visible proposée, arrangées comme un amas de grains de sable, qu'on auroit applani autant qu'il en est capable; cette surface alors devient égale comme un verre poli à nostre égard; & quoiqu'elle demeure tousjours raboteuse à l'egard des particules de l'Ether, il est evident que les centres de toutes les spheres particulieres de reflexion, dont nous avons parlé, sont à peu prés dans un mesme plan uni, & qu'ainsi la commune tangente leur peut convenir assez parsaitement pour ce qu'il faut à la production de la lumiere. Et c'est ce qui seulement est requis, dans nostre maniere de demonstrer, pour faire l'égalité desdits angles, sans que le reste du mouvement reflechi de toutes parts puisse produire aucun effet contraire.

+ (p. 26).