Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 444]

XII.
Quelques considérations ultérieures sur les ondes dans le cristal d'islande, e.a. sur celles qui traversent deux cristaux successivement. La réflexion intérieure dans le cas du même cristal.
[1679]

§ 1¹⁾.

In situ parallelo crystallorum duorum naturali figura praeditorum unusquisque e bifidis radijs suam tantum movet materiam²⁾.

In refractione per 2 crystalla. Cum radius est in plano per utrumque axem ducto et in superficiem secundo loco refringentem perpendiculari³⁾, unusquisque e bifidis radijs non nisi suam materiam movet²⁾. Cum vero planum per radium et per axem ultimo refringentis secat axem primum refringentis angulo 45 graduum tunc unaquaeque materia non suam sed alteram vicissim movet. Attamen hic in obliquiore incidentia radij unaquaeque utramque movet⁴⁾.

1) La Pièce XII est empruntée aux p. 206-208 du Manuscrit E. Les p. 202 et 221 sont respectivement datées ‘a Paris le 14 Aoust 1679’ et ‘a Paris 11 Jan. 1680’.

2) Cette hypothèse s'accorde avec celle de 1672 ou 1673 du Manuscrit D (§ 8 de la Pièce I qui précède), où Huygens avait déjà dit qu'elle n'explique pourtant pas les phénomènes observés lorsque les rayons passent successivement par deux cristaux non parallèles.
Observons cependant que Huygens parle ici simplement de ‘bifidi radij’, tandis qu'en 1672 il parlait des ‘deux divers mouvements d'undulation [des] deux matieres de l'éther’.
Dans le Traité de la Lumière (par. 18 et 19 du Chap. V) il parle de ‘deux différentes émanations d'ondes de lumière’, dont l'une, la régulière, se ferait ‘dans la matiere étherée repandue dans le corps du cristal’ et l'autre tant dans cette même matière ‘que dans les particules dont [le cristal] est composé’.
Dans la [lettre à Papin du 14 décembre 1690 (T. X, p. 178) Huygens émet l'hypothése que la réfraction irrégulière pourrait se faire par des ondes s'étendant dans trois matières, savoir, outre les deux déjà mentionnées, ‘une autre qui occupe les intervalles qui restent autour des ... spheroides [c.à.d. des particules composantes] et qui sert a les tenir joints ensemble’.

3) Ici Huygens ne suppose plus - comparez la p. 517 qui suit - ‘que les deux surfaces qui se regardent soient paralleles’.

2) Cette hypothèse s'accorde avec celle de 1672 ou 1673 du Manuscrit D (§ 8 de la Pièce I qui précède), où Huygens avait déjà dit qu'elle n'explique pourtant pas les phénomènes observés lorsque les rayons passent successivement par deux cristaux non parallèles.
Observons cependant que Huygens parle ici simplement de ‘bifidi radij’, tandis qu'en 1672 il parlait des ‘deux divers mouvements d'undulation [des] deux matieres de l'éther’.
Dans le Traité de la Lumière (par. 18 et 19 du Chap. V) il parle de ‘deux différentes émanations d'ondes de lumière’, dont l'une, la régulière, se ferait ‘dans la matiere étherée repandue dans le corps du cristal’ et l'autre tant dans cette même matière ‘que dans les particules dont [le cristal] est composé’.
Dans la [lettre à Papin du 14 décembre 1690 (T. X, p. 178) Huygens émet l'hypothése que la réfraction irrégulière pourrait se faire par des ondes s'étendant dans trois matières, savoir, outre les deux déjà mentionnées, ‘une autre qui occupe les intervalles qui restent autour des ... spheroides [c.à.d. des particules composantes] et qui sert a les tenir joints ensemble’.

4) Huygens suppose ici que le rayon incident, se trouvant sans doute dans le plan de la section principale du premier cristal, fasse avec l'axe optique un angle aigu de 45^o au moins. Dans ce cas il est possible de mener par le rayon (ou plutôt par l'un quelconque des deux rayons parallèles au rayon incident qui ont traversé le cristal) un plan (ou deux plans) P faisant avec l'axe optique un angle de 45^o. L'axe optique du deuxième cristal est par hypothèse situé dans le plan P.
Le cas le plus simple est celui où le rayon incident (considérons-le comme vertical) est perpendiculaire à la face supérieure du premier cristal. En effet, puisque l'axe optique fait avec cette face un angle qui ne diffère guère de 45^o (p. 427 qui précède), le plan P est alors à peu près perpendiculaire à la section principale du premier cristal; et le deuxième cristal peut avoir ses faces horizontales parallèles à celles du premier, tandis que sa section principale n'est autre que le plan P. Huygens disait déjà en 1672 ou 1673, (Pièce I, § 7) que dans les cristaux à faces horizontales parallèles et dont les sections principales sont perpendiculaires entr'elles - cristaux croisés -, le rayon ordinaire (p.e. vertical; avant-dernier alinéa du § 7) produit par réfraction un rayon extraordinaire et réciproquement.

[p. 445]

§ 2.

In reflexione intrinseca unius crystalli. Cum radius est in plano per axem ducto et in superficiem reflectentem perpendiculari unusquisque è bifidis non nisi suam materiam movet⁵⁾; alias utramque, sed est exceptio⁶⁾.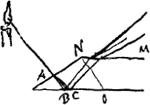

[Fig. 168.]

[Fig. 169.]

5) Dans le § 5 qui suit Huygens semble considérer le cas où un rayon extraordinaire non situé dans une section principale produit par réflexion intérieure un rayon ordinaire.

6) Il n'est pas clair quels sont les autres cas où exceptionnellement, suivant Huygens, un rayon produit par réflexion intérieure un rayon unique. Il peut avoir songé à son expérience du § 3 [Fig. 168].

§ 3.

Hic [Fig. 168] duae tantum imagines fiunt etsi radij AB, AC non sint in plano per axem crystalli ducto et in planum reflectens perpendiculari. Sectio NO facienda ut appareat an parallelismus NM, BO, impediat duplicationem radiorum⁷⁾.

7) Nous ne trouvons pas que Huygens ait fait cette expérience. Il aurait pu constater qu'en effet les rayons AB et AC de la Fig. 168 peuvent produire chacun deux rayons par réflexion intérieure.
Bartholinus avait déjà constaté (Exper. XI des ‘Experimenta crystalli Islandici etc.’) que les rayons peuvent être doublés de cette manière.

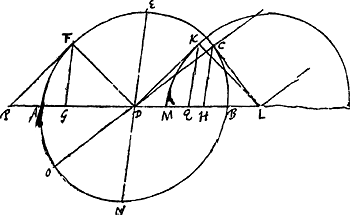
§ 4. Invenire reflexionem intrinsecam Crystalli Islandicae in materia refractionis anomalae⁸⁾.

Sit CD [Fig. 169] radius intra crystallum cujus superficies AB. Spheroidis positio qualis AECBN circà centrum D. Sit EDN diameter conjugata AB. CH parallela ED.

8) Il s'agit d'une réflexion intérieure, où le rayon extraordinaire situé dans le plan principal produit par réflexion un nouveau rayon extraordinaire, évidemment situé dans le même plan.

[p. 446]

DG aequalis DH, GF parallela ED. Erit DF reflexio radij CD.

Demonstratio. CL tangens est undae portio, secundum quam extenditur radius CD. Dum vero punctum C venit in D, punctum undae L undam spheroidem MK aequalem et similiter positam ipsi AEB genuisse debet, cujus tangens DK est itaque reflexio undae CD [lisez plutôt: undae CL] cum C est in D, per theoriam nostram in libro dioptricae explicatam⁹⁾. Ergo LK, et ipsi parallela ex D puncto educta, terminant progressum undae DK factae ex reflexione undae CL. Atqui parallela ista est DF, nam quia DG aequalis DH, et GF, HC ordinatim applicatae ad diametrum AB, sunt et GF, HC aequales, et ductis tangentibus FP, CL, fiunt aequales DP, DL, quia proportionales PD, AD, GD, itemque LD, BD, HD. Atqui LM aequalis est DA. Ergo MD aequalis AP. Et propter paritatem ellipsium MK, AF, quarum tangentes DK et PF, si ducatur LK ad punctum contactus, erunt singulae DK, KL aequales singulis PF, FD. Sunt autem et DL, DP aequales. Ergo LK parallela DF ut dicebamus. Cum ergo LK, DF terminent utrimque progressum undae reflexae DK, erit DF progressus puncti D postquam venit per CD.

9) Le Traité de la Lumière avait été rédigé en 1678. Comparez la p. de l'Avertissement.

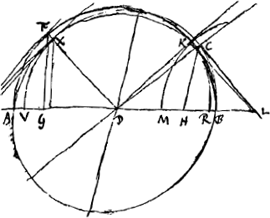
§ 5.

Radius incidens [Fig. 170] CD. ACB spheroides. CH ordinatim applicata ad AB. Ut DB ad semiaxem spheroidis sive minorem diametrum ellipsis ACB ita DH ad DG. AFB semicirculus. GF perpendicularis AB. DF est reflexio radij CD, in materiam analogam ex anomala¹⁰⁾.

10) La construction qui suit fait voir que Huygens entend parler ici d'une réflexion intérieure, où le rayon extraordinaire incident produit par réflexion un rayon ordinaire; la ‘materia analoga’ est donc la matière éthérée dans laquelle se propagent les rayons, ou les ondes, ordinaires.
On voit dans la Fig. 170 que le rayon réfléchi considéré est ordinaire, puisque DK est ici tangente à une circonférence de cercle, tandis que dans la Fig. 169 DK touchait à une ellipse. Les points H et L sont les mêmes dans les deux figures, mais les points G et par conséquent aussi les points P sont différents.

[p. 447]

[Fig. 170.]

[Fig. 171.]

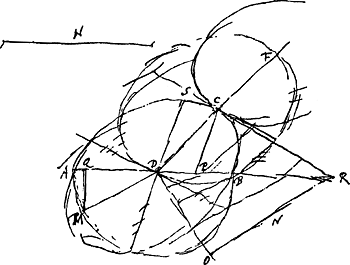
Demonstratio. Sit DH ⫟ DB - DB ⫟ DL.

ML ∞ semiaxis. MK arcus circuli centro L. DK tangens. Jam DK est reflexio undae CL.

§ 4. Chaque endroit d'onde spheroide aussi bien que spherique s'avance parallelement a la tangente en cet endroit. et suivant la direction de celle qui du centre est menée a cet endroit. Cela se demonstre de mesme qu'il a estè fait dans les ondes spheriques.

Du centre D soit descrite l'ellipse ACB qui marque la section de l'onde spheroide née du point D. Et soit CR [Fig. 171] tangente en C. laquelle representera une portion d'onde ayant le centre fort eloignè; de la quelle portion le point C s'avance suivant CD. Car la ligne CD venant du centre d'une ellipse qui est vers F, semblable et semblablement posée à l'ellipse ACB, a cause de la disposition du cristal, CR sera aussi tangente en C de cette autre ellipse, et en representera une portion si on concoit l'ellipse infiniment grande.