Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 439]

XI.
Lecture de ‘la dioptrique’, c.à.d. du traité de la lumière, en diverses séances de l'académie des sciences, et pièces sur la réfraction du cristal d'islande écrites dans le cours de cette lecture.
1679.

Registres de l'Académie, T. VII. Les f 176 r et 185 r mentionnent le retour de Huygens à Paris en juillet 1678 et le ‘nouveau microscope’ qu'il apporta ‘qui est d'une petitesse extraordinaire et comme un grain de sable et qui grossit les objets d'une maniere incroyable’. Nous avons publié un extrait des Registres de juillet dans la note 1 de la p. 96 du T. VIII. Voyez aussi les p. CVII et 678-679 du T. XIII.

Le samedi 6 août 1678 il est dit (f. 186r): ‘Samedy prochain M^r. Hugens parlera des refractions’. Toutefois Huygens le 13 août (f. 196r) ne parla pas de ce sujet mais ‘des lieux plans d'Apollonius’. Nous apprenons ensuite que le 20 août 1678 ‘M^r. Roëmer a apporté une nouvelle maniere de microscopes de M^r. Hugens qui presente plusieurs objets successivement par le moyen d'une roüe’. Voyez les p. 98, 99 et 112 du T. VIII, 680 et suiv. du T. XIII. Les Registres font mention (d'observations faites le 6 mai 1679¹⁾.

Avant le retour de Huygens d'autres membres - le discours de Römer a été mentionné dans la Pièce III - avaient parlé de la réfraction²⁾. En avril 1678 (T. VII, p. 149) ‘M^r. Mariotte a commencé aussy de donner les demonstrations touchant les couleurs de l'arc-en-ciel, et du prisme de verre qui font une partie de son traitté d'optique’. Mariotte parla de nouveau sur la lumière après le retour de Huygens (T. VII, f. 239 v, le samedi 11 mars 1679): ‘Messieurs Mariotte et de la Hire ont parlé de quelques obseruations qu'ils ont faittes sur les refractions de la lumiere, qui passant par un petit trou, et tombant perpendiculairement sur la premiere surface se rompent dans la 2e surface ... etc. Ils ont encore parlé d'autres obseruations qu'ils ont faittes, que M^r. Mariotte donnera comme l'explication du second arc-en-ciel’.

1) Registres, T. VII f. 244 (le 6 mai 1679): ‘M^r. Picard a fait voir par le microscope de M^r. Hugens la poussiere qui se trouve dans l'heliotropium majus Americanum ou grand soleil qui paroist comme des boules avec des rayons, et celle du trifolium acetosum dont les parties sont rondes, et comme percées par le milieu, et de la jonquille qui paroist comme des pigeons d'Inde. On a veu aussy la poussiere qui paroist sur les aisles des papillons, qui paroist auec trois pointes, et rayée. On a aussy veu l'enueloppe exterieure de la paille, qui paroist rayée, et on voit entre les rayes comme une espece de vis ou chainette ondée. Le moelle d'une plume paroist comme un raiseau. On a veu aussy un petit morceau de sapin avec une infinité de petits cercles concentriques et des fibres en quelques lieux transuersales’.

2) Le 26 mars 1678 (Registres, T. VII, f. 141 v) ‘M^r. Carcaui a proposé de faire une optique entiere; Messieurs Mariotte, Picard et de la Hire y trauailleront conjointement’.

[p. 440]

Le samedi 13 mai 1679 (f. 244 v.) ‘on a commencé a lire le traitté de M^r. Hugens de la Dioptrique’. Le 20 mai ‘on a continué la lecture de la Dioptrique de M^r. Hugens’. Le 27 mai M^r. Hugens a continué la lecture de sa Dioptrique’. Le 3 juin ‘on a continué la lecture de la Dioptrique de M^r. Hugens’. Le 10 juin ‘en lisant la Dioptrique de M^r. Hugens on a proposé de faire quelques expériences sur la compressibilité de l'eau [comparez la p. 482 qui suit du Traité de la Lumière] par le moyen des vaisseaux de metal qu'on remplira d'eau, et estans bien bouchez on les battra fortement, et en faisant quelque ouverture on verra si l'eau rejaillit [nous avons déjà cité ce passage à la p. 334 qui précède]. On a proposé aussi de faire des experiences sur les sels dissouts dans l'éau, pour voir s'ils font hausser l'eau³⁾. La f. 252 du T. VII parle de nouveau du microscope et des lieux plans d'Apollonius et dit aussi, évidemment en récapitulant: ‘M^r. Hugens a aussi beaucoup trauaillé sur la Dioptrique et on a commencé a lire la premiere partie de son traitté qui contient les raisons physiques de la réfraction et des phenomenes du cristal d'Islande’. F. 152 v (1 juillet 1679): ‘M^r. Hugens a continué la lecture de son traitté de la Dioptrique’.

3) Le 17 juin suivant ‘on a vérifié l'experience de la dissolution du sel dans l'eau rapportée par plusieurs autheurs et on a trouué que le sel dissout n'augmentoit pas le volume de l'eau’.

A. Observation faite le 3 Juillet 1679. qui prouve manifestement que ce n'est pas le rayon parallele aux costez du cristal qui passe sans refraction comme j'avois creu jusqu'icy⁴⁾.

CA [Fig. 163] est la surface superieure du cristal. C [Fig. 164] l'angle solide obtus compris de 3 angles plans obtus egaux chacun a KCK. Ayant marquè un point D dans cette surface, il faut sur la surface opposée trouver le point B directement opposè à D suivant l'obliquitè du cristal, c'est a dire que la droite qui joint ces points, en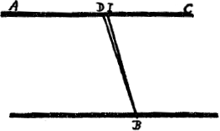

[Fig. 163.]

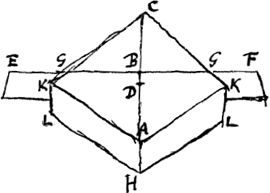[Fig. 164.]

traversant le cristal, soit parallele aux costez AH, KL. Puis ayant mis une regle platte

4) Consultez sur cette Pièce, tirée du Manuscrit D, p. 358, la note 2 de la p. 410 qui précède.

[p. 441]

EF sous le cristal a angles droits au diametre et dont le costè EF passe par le point du fond B, il faut regarder cette regle a travers l'epaisseur du cristal et placer l'oeil en sorte que tout le costè EF paroisse une ligne droite, scavoir le costè EF qui paroit par la refraction irreguliere qui est celle qui donne l'image plus basse que l'autre refraction.

Ce lieu de l'oeil estant trouvè il faut marquer dans le diametre CA le lieu ou paroit le point B, qui sera different du point D, ce qui prouve que ce n'est pas le rayon qui joint les points D B ni aucun a luy parallele qui passe sans refraction, mais scachant la distance entre D et le point ou paroit B dans la mesme surface superieure, avec l'epesseur du cristal, l'on trouvera l'inclination du rayon qui joint B et le point de son apparence, et c'est cettuicy et ses paralleles qui passent sans refraction.

Dans cette autre figure [Fig. 163] qui represente la section du cristal par le diametre AC, DB est la ligne qui joint les points D, B, parallele aux costez du cristal. IB celle qui joint le point B avec le point I, où B paroit dans le diametre AC. Et l'angle DIB est de 2 1/2 degrez environ. IB le rayon qui passe sans refraction.

Registres, T. VII, f. 252 v (8 juillet 1679): ‘La Compagnie estant assemblee, M^r. Hugens a continué la lecture de son traitté de la Dioptrique’. F. 255 v. (15 juillet 1679): ‘On a continué la lecture de la Dioptrique de M^r. Hugens’. (22 juillet): ‘M^r. Hugens a continué la lecture de sa Dioptrique’¹⁾.

1) Registres, T. VIII, f. 222 v. (19 juillet 1679): ‘M^r. Mariotte a commencé de lire son traitté des couleurs’. Il en continua la lecture le 9 août, etc. Comparez la note 1 de la p. 362 du T. XVII.

B. A Paris 6 Aoust 1679. ʿEYRHKA. La confirmation de ma theorie de la lumiere et des refractions²⁾.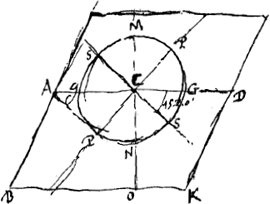

[Fig. 165.]

ABKD [Fig. 165] la section principale du cristal qui divise l'angle obtus des faces opposees en deux egalement. gSG le spheroide dans lequel s'estend la lumiere dans le cristal. SCS l'axe du spheroide. PP le grand diametre.

Comme la refraction irreguliere de la surface AD se regle par le demispheroide gNG, ainsi en coupant le cristal par le plan MCO, la refraction de la surface MO se doit regler par le demi-

2) Manuscrit E, p. 197-198.

[p. 442]

spheroide NGM. Et si on le coupe par le plan PCP la refraction de la surface PP se doit regler par l'hemispheroide PSP, et ainsi des autres. Or comme l'angle GCS que fait l'axe du spheroide SC sur le plan gG est de 45.20′, si le plan MN est pris en sorte que l'angle SCN que l'axe CS fait sur luy soit de mesme de 45.20′, les demispheroides GNG, MGN seront pareils et semblables; et il s'en suivra, si nostre theorie est vraye, que la surface MNO fera toutes les mesmes refractions que la surface gG. Et non seulement la surface MNO, mais toute autre dont le plan couppera le cristal en sorte que l'axe SS soit inclinè sur luy d'un pareil angle de 45.20′. De sorte qu'il y a une infinitè de telles couppes qui doivent produire precisement les mesmes refractions que la couppe naturelle suivant AD. Souhaitant donc de voir cette grande preuve de la veritè de mon hypothese et par consequent de toute ma theorie de la lumiere et des refractions, j'ay taschè de trouver quelque moyen de polir cette pierre apres l'avoir couppée en differentes manieres.

Ce poli est tres difficile et ne succede point par les voies ordinaires dont on se sert pour les autres corps. Mais j'y ay a la fin reussi en frottant premierement les surfaces sur des limes plattes et fort fines; puis sur des pierres a eguiser qui servent aux rasoirs; puis en dernier lieu sur une glace de miroir que j'avois fait depolir et bien doucir en suite. Cela donne un assez bon poli a ce cristal pour pouvoir remarquer ce qui s'y passe dedans pour la refraction; et en addoucissant encore plus la glace du miroir, je crois qu'on viendroit a plus grande perfection. Mais n'estant qu'a peu pres poli, si on graisse la surface avec de l'huile d'amandes, que l'on rend uni en passant une regle dessus, alors elle devient transparente a peu pres comme les surfaces qui se font en fendant le cristal¹⁾.

De cette maniere j'ay fait la section MNO, et j'ay trouvè que les surfaces qu'elle a faites avoient les mesmes refractions que la surface gG, d'ou je crois que toutes celles qui seront egalement inclinees a l'axe SS feront encore la mesme chose.

J'ay aussi fait la section par le plan SS, qui ne rompt point le rayon perpendiculaire, comme aussi elle ne devoit point suivant nostre theorie. Mais en regardant obliquement on appercoit deux images de l'object l'une au dessus de l'autre. Et cela est de mesme dans la section que j'ay faite par ASPS.

Je puis faire une piramide quarree, pentagone, hexagone ou de tant d'angles qu'on voudra de ce cristal. et qui soit equilaterale, dont toutes les surfaces plattes fassent la mesme refraction. Ces surfaces feront avec l'axe du cristal un angle de 45^o.20′. J'en puis faire [Fig. 166] des rhomboides semblables a celuy qui est le naturel, qui fassent de tous les costez les mesmes refractions que le naturel, et qui pourtant se fendent tout autrement. J'en puis aussi faire des prismes triangulaires ou de tant de costez que je veux dont les bases ni les costez ne rompront point le rayon perpendiculaire, quoy-

1) Huygens ajouta plus tard dans l'interligne: Voiez une meilleure maniere de ce poli cydessous, apres 5 seuilles. Mais on n'en trouve rien dans le Manuscrit. Comparez sur la nouvelle manière la p. 516 qui suit.

[p. 443]

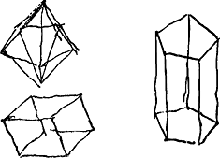[Fig. 166.]

[Fig. 167.]

que pourtant ils fassent tous double refraction. le cube est compris parmy ces prismes. les bases sont des sections perpendiculaires a l'axe du cristal et les costez des sections paralleles a l'axe.

Il paroit que ce n'est point la disposition des feuilles du cristal qui contribue a la refraction irreguliere.

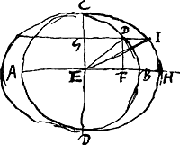
C. Pour les spheroides des ondes de la lumiere dans le Cristal d'Islande²⁾.

AB et CD [Fig. 167] estant des diametres d'un cercle qui se couppent a angles droits, s'il y a un mouvement qui s'estende du centre E vers la circonference en ligne droite (ED), et que du point D l'on tire les perpendiculaires DF, DG sur les diametres AB, CD, l'on scait que ce mouvement se peut considerer comme composè de deux mouvements l'un vers B l'autre vers C. Et dont les lignes EF, EG representent les vitesses, ou bien les espaces passez en mesmes temps. Que si le mouvement vers C demeurant le mesme, l'autre mouvement vers B est augmentè en certaine raison, comme de EB à EH, il est evident que le mouvement qui auparavant se seroit estendu par ED, s'estendra par EI, en sorte que la droite IDG soit à DG comme HB à EB. Parce qu'il faut que l'espace passè par le mouvement de E vers C soit le mesme qu'auparavant sçavoir EG, et que l'espace passè par le mouvement de E vers B soit plus grand que EF ou GD, suivant la raison de HE à EB. Or le point I est dans l'ellipse dont le demi grand diametre est EH et le demi petit diametre EC, par la proprietè connuë de cette figure. D'icy il est aisè de comprendre, si ACBD est une sphere, et CHD un spheroide ayant le mesme axe CD, que le mouvement qui estant egal de tous costez autour du centre E, s'estendroit en sphere, s'estendra en ce spheroide CHD, si le mouvement autour de l'axe CD est tousjours augmentè suivant la raison de HE à EB. Parce qu'un spheroide n'est autre chose qu'une sphere elargie ou restrecie proportionnellement dans le sens des perpendiculaires à l'axe.

Registres, T. VII, f. 256: ‘Le Samedy 12e d'Aoust 1679, la Compagnie estant assemblée, on a continué la lecture de la Dioptrique de M^r. Hugens’.

2) Manuscrit E, p. 199-200.