Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695
(1937)–Christiaan Huygens–
[pagina 432]
| |
VIII.
| |
[pagina 433]
| |
novembre (T. VIII, p. 42) qu'en effet ‘illi indicium debetur, ego rem aliter atque ille examinavi’. Avant de rédiger sa deuxième lettre qui se rapporte à ce sujet Huygens écrivit dans le Manuscrit E (p. 99-101) la Pièce qui suit. Elle sert (voyez la fin) à démontrer le théorème de Römer (lettre du 1 nov.) imprimé en italiques à la p. 39 du T. VIII. 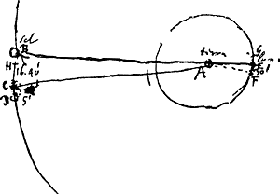 [Fig. 157.]
§ 1. Tychonica vel Ptolemaica hypothesis. Sit terra in A [Fig. 157] immobilis, B sol, cujus lux ut perveniat in A opus erit 400 horis, si opus est una hora ad peragendum intervallum quo a nobis abest luna nempe 30 diametrorum terrestrium. cum ego a terra ad solem statuam 12000 diametros terrestres. Hinc sequitur eo momento quo solis ex B progressi lux ad terram A pertinget, solem fore in C, ita ut angulus BAC sit 16 gr. 40′. quia nempe in 24 horis conficit grad. unum. Quod si jam eodem momento luna foret in E, ita ut BAE sit recta linea; observatio non contingeret lunam, quia umbra seu defectus luminis post horam demum perveniet in E, adeo ut luna jam 30′ inde progressa foret. Necesse est igitur, si luna illâ observatione contingi debet, ut eo momento quo lux solis pervenit in A, ipsa fuerit in F. 30′ anterior puncto E. Sic enim invenietur eodem instanti in E quo et umbra terrae eo pervenerit. Terra autem obscurationem lunae post horam demum a tempore quo contigit perceptura est, hoc est duabus horis posterius quam lux solis ad A pervenerit. Istis autem duabus horis sol à C ad D motus est per 5 min. Ergo terrae apparitura est luna obscurata in E cum sol erit in D, ipsa vero luna in G, posito arcu EG 30′. Sol vero non apparebit in D, sed in H ita ut arcus BH sit tantum 5 min. Etenim eo momento quo lux solis ex B egressa pervenit in A, solis apparens locus est in B, ideoque 6 [lisez 2] horis post in H. Itaque in hypothesi Tychoniana luna eclipsata observaretur cum 5 min. adhuc a loco opposito soli apparenti abest. Sed a loco opposito soli vero, 16 gr. 40′ min. Atque haec posito illo horario luminis trajectu à luna ad nos. Si vero a sole ad nos perveniat lux 11 minutis horarijs ut invenit RomerusGa naar voetnoot1), erit plane inobservabilis differentia lunae eclipsatae a puncto oppositionis apparente. | |
[pagina 434]
| |
Lunae observatae locus observatus sequitur locum oppositum soli apparenti angulo duplo ejus quem peragit sol dum lux trajicit spatium quo luna a nobis abest [comparez la fin du § 2]. Hic non refert quanta sit solis distantia. 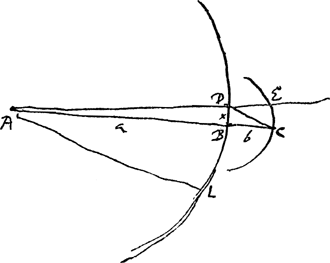 [Fig. 158.]
Comparez la figure de la p. 43 du T. VIII. § 2. A sol [Fig. 158]. BD orbita terrae annua. BC distantia lunae. Arcus BD quem terra percurrit dum lux bis peragit spatium BC. Quaeritur angulus DCB quo luna observata sequitur oppositionem observatam. n tempus lucis per AB. c spatium motus horarij terrae in orbita sua. h tempus horae. BD ∞ x. 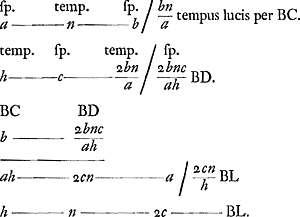 | |
[pagina 435]
| |
c est hic tempus per arcum orbitae terrestris 2 1/2 min. [ou plutôt: c est la longueur d'un arc de 2½ min.]. 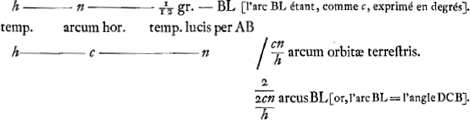 Ceci correspond à l'avant-dernier alinéa du § 1.
Absque ullo calculo. Si BD est arcus quem percurrit terra dum lux bis peragit spatium BC, sequitur ducta AL parallela CD, fore BL arcum quem percurret terra dum lux bis peragit spatium AB. Ergo cum notus sit arcus horae tempore emensus a terra in orbita sua notumque ponatur tempus quo lux peragit spatium AB, noscetur et arcus BL, cujus gradus aequantur gradibus anguli DCB quo luna obscurata sequitur oppositionem observatam. Est enim angulus BAL tot graduum quot percurreret terra eo tempore quo lux peragit duplum spatium AB. Atque hoc est Theorema RomeriGa naar voetnoot1). Dignum notatu autem quod non referat quae sit lunae à terrisGa naar voetnoot2) distantia.
Theorema Romeri ita habet. Umbra terrae motae, ubilubet extra terram è terra visa, sequitur punctum oppositum soli, extra terram è terra visa, duplo angulo quo promovetur terra circa solem interea dum lumen ab eo ad nos perveniat.
Cette Pièce est suivie par un projet de la lettre à Römer du 18 novembre 1677. Nous avons fait mention de ce projet dans la note 1 de la p. 42 du T. VIII. |
|

