Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 428]

VII.
Explication, par ondes sphéroïdales, de la réfraction extraordinaire du cristal d'islande. arrangement régulier des particules qui constituent le cristal.
1677.

§ 1¹⁾. ʿEYRHKA 6 Aug. 1677. Causam mirae refractionis in Crystallo Islandica.

AC [Fig. 151] radius recta penetrans. AB refractio radij perpendicularis. AS axis anguli solidi obtusi. AP perpendicularis AS, axis ellipseos seu spheroidis, tangentis BD in B. Bγ, Bδ perpendiculares in AP, AS. AP media proportionalis inter Aγ, AD. Item AS media proportionalis inter Aδ, Aζ [d'où résulte que Dζ touche l'ellipse au point B].

ϰμ parallela tangenti in C, μL parallela AC. angulus μLA rectus.

Quo tempore lux in aere facit sphaeram cujus radius μL, eadem intra crystallum facit spheroides πϰη simile PCH [on voit que le petit axe de l'ellipse πϰη est égal, ou peu s'en faut, aux ⅗ de μL; comparez le paragraphe 33 du Chap. V du Traité de la Lumière].

Ut μL ad Aη ita KA ad HA. fit AE (ducta ad contactum KE) refractio radij maximè inclinati μA. vel in minori spheroide posita ϰA aequali Lμ, et ducta Aε ad contactum ϰε [c'est un cas particulier de la construction du § 2 qui suit, ou bien du paragraphe 28 du Chap. V du Traité de la Lumière, où le rayon incident ne rase pas la surface, mais fait avec elle un angle quelconque].

Videndum an AH ∞ AI [on aurait AH = AI, I étant un point de l'ellipse et non pas de la tangente en B, si l'angle KAS, et par conséquent aussi l'angle IAS (AI étant par hypothèse perpendiculaire à AK), était de 45^o; d'après le paragraphe 26 du Chap. V du Traité de la Lumière le calcul de cet angle conduisit Huygens - comparez la Pièce XIB à la p. 441 qui suit - à la valeur 45^o20′]. Tunc semper refractio ordinaria fieret sed ita ut sinus intra crystallum applicetur ad diametrum ellipsis AB [voir sur cette proposition le § 2 qui suit].

1) Les §§ 1 et 2 sont empruntés à la p. 93 du Manuscrit E.

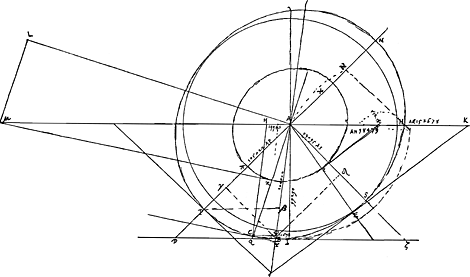
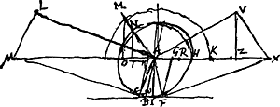
§ 2.

Cμ tangens in C [Fig. 152]. μL parallela CA. μLA rectus. MA radius incidens. AV perpendicularis MA. AVX rectus. VX ∞ μL. XF tangit ellipsin. AF est refractio radij MA. Sit AM ∞ VX vel Lμ. FG parallela BA. Ergo proportionales XA, HA, GA. sed et proportionales AX, XV, XZ. Ergo XZ vel AO ad AG ut qu. XV sive qu. MA ad qu. HA.

[p. *10]

[Fig. 151.]

[p. 429]

[Fig. 152.]

[Fig. 153.]

[Fig. 154.]

Sit ut MA seu KA ad HA ita haec ad RA. Ergo jam AG ad AO ut AR ad AK. sed AO ad AT (facto semicirculo HN) ut MN ad NA seu KA ad AN. Ergo ex aequo AG ad AT ut AR ad AH sive ut AH ad AK.

Lμ, sive AK ad AH ut 152678 ad 98470 [ce qui est un peu inférieur à 8/5; comparez sur cette dernière fraction la p. 411 qui précède].

On a donc AG : AH = AT : AK. Or, suivant la Fig. 152,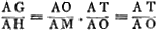 sin i, où i désigne l'angle d'incidence du rayon MA.

D'autre part AG/AH = AG/AI lorsque AI = AH (fin du § 1). Si nous appelons sin r le rapport AG/AI, on aura donc sin i/sin r = AO/AT = Lμ/AH = constante, bien entendu en considérant AI comme égale à AH. C.Q.F.D.

Mais on peut plus simplement considérer, comme Huygens le fera au par. 32 du Traité de la Lumière, la constance du rapport AT/AG et dire que c'est celui d'un sinus linéaire AT à une espèce de ‘sinus intra crystallum applicatus ad diametrum ellipsis AB (§ 1 qui précède)’. Alors la condition AI = AH ou ∠ KAS = 45^o n'est plus nécessaire.

D'après la Fig. 151 Huygens trouva, en posant AB = 100000 : AP = 105022, AS = 93095, AI ou AI′ = 99290, AH = 98473, AK = 152678, BI′ = 11898 (I′ désignant le point de la tangente au point B situé sous le point I).

Les calculs du Traité de la Lumière conduisent à des résultats un peu différents, savoir AP = 105032, AS = 93410, AI′ = 99324, AH = 98779, AK (ou N) = 156962, BI′ = 11609 (par. 27, 30 et calculs à la fin du Chap. V).

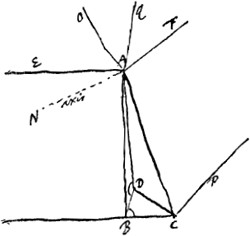
§ 3.

Les p. 86-96 du Manuscrit E contiennent beaucoup de calculs numériques que nous ne croyons pas devoir reproduire puisque les résultats obtenus plus tard furent différents (voir la fin du § 2). En voici un échantillon.

Les Fig. 154 font voir que Huygens se servait en 1677 de triangles sphèriques.

[p. 430]

Ex positis a Bartholino fit ABD 76.22′ et OAC 72.34′. Si sumamus ABD 75.54′ tunc angulus OAC fit 72^o.0′, nempe angulus pentagoni. Et EAC 101.18′.

Si EAC 101.27′, fiet ABD 75.40′. Si EAC 101.33′, fiet OAN 45^o. C'est l'angle dont il s'agissait à la fin du § 1; et qui plus tard fut trouvé égal à 45^o20′.

§ 4.

Les p. 182-196 du Manuscrit E sont également remplis de calculs numériques sur la réfraction du cristal d'Islande. Les lignes qui suivent sont empruntées aux p. 182 et 186.

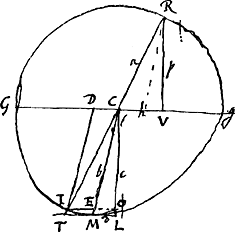
Refractio regularis paulo major ex ultima exactissima observatione quam 5 ad 3, et optimè convenu cum ista 500 ad 293.

Elevatio fundi minima major observata plurimis vicibus quam fiebat posita N 153456, et ad minimum quanta est ponendo N ∞ 158928. Voyez sur N la fin du § 2 qui précède ainsi que la Fig. 171 qui suit et le par. 28 du Chap. V du Traité de la Lumière.

Angulus radij transeuntis sine refractione fuit circiter 73 gr. quantus ad minimum est ex observatione exacta. L'angle est de 73^o20′ d'après le par. 16 du Chap. V du Traité de la Lumière.

Posita N 158928 et proportione refractionis regularis 500 ad 293 fit ratio N ad minorem spheroidis axem eadem quae N ad radium sphaerae extensionis luminis in refractione regulari.

CR, CG ∞ a ∞ 98473 [Fig. 155]. sin. c. 6.50′ ∞ CL ∞ c 00 99290. sin 6.50′ ∞ LM ∞ d ∞ 11898. CM ∞ rad. 100000 [comme au § 2].

N ad CG proximè major quam 8 ad 5 [puisque la valeur adoptée pour N est ici plus grande qu'au § 2].

Crassitudo cristalli quo ad observationes usus sum 3 pollicum parisiensium.

Comparez la Fig. 155 avec celles du par. 40 du Chap. V du Traité de la Lumière. À la p. 184 du Manuscrit E se trouve une figure analogue à celle [Fig. 206] du par. 42. Seulement dans le Manuscrit le calcul avait conduit aux nombres 99290, 71875, 63190 au lieu de ceux (99324, 70283, 62163) du par. 42.

[p. 431]

[Fig. 155.]

§ 5.

Les figures [Fig. 156] font voir qu'en 1677 Huygens supposait déjà le cristal composé de particules sphériques ou sphéroïdales. C'est cette dernière forme qu'il adopte dans le Chap. V du Traité de la Lumière (p. 519-521 qui suivent). Voyez aussi l'Appendice III à la p. 544 qui suit.

[Fig. 156.]¹⁾

1) Manuscrit E, p. 93.