XII.
Remarque sur l'oscillation cycloidale du pendule triangulaire. horloge réglée par la circulation de deux billes placées dans un canal parabolique.
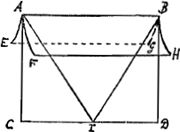
À la p. 16 du T. XVIII nous avons dit, en parlant du pendule triangulaire de l'horloge marine représentée en cet endroit [Fig. 10 et 11] que Huygens ne pouvait guère savoir, puisqu'il ne semblait pas avoir examiné la question, si les oscillations du point I [Fig. 93], suspendu à des cordes
obliques A I et B I, venant s'appliquer sur des cylindres cycloïdaux A E G B et A F H B, jouissent
[Fig. 93.]
de la propriété de l'isochronisme.
Or, Mons. J. Yzerdraat, qui s'occupe avec M. Muller von Czernicki - voir la p. 547 du T. XVII - de la reconstruction des horloges de HuygensGa naar voetnoot1), nous a fait remarquer qu'on peut aisément démontrer que l'isochronisme subsiste dans le cas de fils obliques. Huygens a sans doute trouvé la démonstration trop évidente pour la mettre par écrit.
Il suffit en effet de démontrer que le point I décrit une cycloïde. Or, il en est ainsi lorsque ce point est suspendu au plan flexible et inextensible ABDC. Par conséquent il en est de même lorsqu'on supprime diverses parties de ce plan, jusqu'à ce qu'il n'en reste plus que les bandes infiniment étroites AI et BI qui, à la limite, deviennent des fils sans épaisseur.
Nous n' avons pas encore reproduit dans le T. XVIII la figure 93 bis (Manuscrit C, p. 216) de l'horloge réglée par la circulation de deux billes placées dans un canal parabolique. On voit que, abstraction faite du moment d'inertie du canal, cette horloge est réglée de la même manière que l'horloge à pendule conique (T. XVIII, p. 11, 363, 437). Nous ignorons si Huygens a fait construire une horloge de ce genre, mais nous en faisons mention ici puisque M. Yzerdraat en a construit une, en même temps qu'une horloge à pendule conique, d'après les projets de M. Muller von Czernicki, lesquelles seront placées dans le ‘Nederlandsch Historisch Natuurwetenschappelijk Museum’ à Leiden.