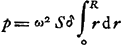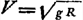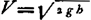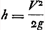Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 166]

XI.
Hydrodynamique¹⁾.

A. § 1²⁾.

Apres avoir considerè les experiences que nous avons faites touchant l'ecoulement et le jalissement de l'eau, je crois qu'on en doibt conclure que la Theorie qu'en a donnse Toricelli fondée sur des semblables experiences est veritable et quoy que l'on trouve parfois que la pratique ne respond pas tout a fait exactement a la speculation, cela ne depend que de quelques circonstances particulieres, les quelles estant bien examinees font veoir la cause de cette difference³⁾.

Nous avons trouvè premierement que deux vases d'egale hauteur mais de differente largeur ayant le fonds percè d'ouvertures egales, et estant entretenus pleins, rendent egale quantitè d'eau en temps egaux, pourveu toutefois que ces ouvertures soient petites a proportion de la largeur des vases; le plus estroit des nostres ayant eu.... pouces, l'autre.... pouces, tous deux la hauteur de.... et le diametre des ouvertures n'estant que de... lignes.

Nous avons aussi trouvè que la surface de l'eau qui s'ecoule descend en parties egales de temps par des espaces inegaux, qui diminuent en mesme proportion comme ceux que passe un corps pesant jetté vers en haut; c'est a dire comme les nombres impairs qui composent le quarrè des parties du temps. Ainsi en divisant la hauteur du vase en 25 parties egales, la surface descend en 5 temps egaux par les espaces decroissans de 9, 7, 5, 3, 1 parties.

La demonstration de cecy et de toutes les autres propositions du traitè de Toricelli dependent d'un effet de la nature qui ne se pouvant jusqu'icy demonstrer par raison

1) Voyez sur cette Pièce la note 4 de la p. 85, ainsi que les notes 4 et 6 de la p. 121 qui précède.

2) Le § 1 de la Pièce A est emprunté aux p. 98-102 du Manuscrit D. La p. 86 porte la date du 28 octobre 1668 (comparez, à la p. 102, le début de la Pièce IV qui précède) et la p. 118 est datée 1669. Toutefois le contenu de ce § doit dater d'avant octobre: voyez le § 2.

3) E. Torricelli ‘De motu aquarum’ dans le Lib. II (‘De motu projectorum’) de ‘De Motu gravium naturaliter descendentium et projectorum Il. duo’ (dans ‘Opera Geometrica’ de 1644, p. 191): ‘Supponimus. Aquas violentèr erumpentes.... etc. (passage déjà cité dans la note 2 de la p. 28 qui précède). Quelques mois plus tard - voyez la note 4 de la p. 171 qui suit - Huygens constata que la différence est parfois considérable.

[p. 167]

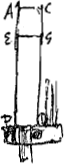[Fig. 88.]

[Fig. 89.]

mais bien par experience doit estre pris pour principe, qui est que les eaux et autres corps parfaitement liquides en sortant par quelque ouverture du vase qui les contient ont la force de remonter aussi haut qu'est leur surface dans le vase³⁾.

De la il est aifè de prouver que l'eau en sortant de quelque ouverture du vase qui la contient doit avoir la mesme vitesse qu'auroit une goute qui seroit tombée de la hauteur que la surface de l'eau du vase a par dessus cette ouverture [Fig. 88]. Car puis qu'un corps acquiert par sa cheute justement autant de mouvement qu'il en faut pour le ramener a la mesme hauteur dont il est descendu, et que l'experience fait veoir que cette eau qui sort de l'ouverture du vase a le mouvement qui est capable de la mener a la hauteur de la surface de l'eau contenue, il s'en suit que ce mouvement doit estre egal a celuy qu'elle auroit acquis en tombant de la hauteur de la surface.

Le premier empeschement qui est la resistance de l'air est d'autant plus grand que l'ouverture D est plus petite, car l'eau s'en dissipe et esparpille d'avantage, et parce que l'air resiste par les surfaces des goutes, qui ont plus grande proportion a la soliditè dans les petites que dans les grandes, il s'en suit que les petites goutes doivent plus ressentir cette resistance que les grandes.

L'autre empeschement qui fait que le jet d'eau ne puisse pas monterjusqu'a la hauteur dela surface BF, est l'eau mesme qui retombe sur elle quand le jet est perpendiculaire, et fait par consequant obstacle a celle qui monte d'enbas. Que si l'on dispose l'ajutage en sorte que le jet ne soit pas perpendiculaire, il ne pourra pas aller si haut que devant par une autre raison, qui est que toute la vistesse de l'eau n'a pas sa direction vers en haut, mais une partie s'en va au mouvement lateral.

Il y a un troisieme empeschement lorsque le vase n'a guere de largeur a proportion de la grandeur de l'ouverture D. parce que l'eau estant contrainte de descendre assez viste et ne se mouvant pas avec une entiere libertè le long des costez du vase à cause de l'adhesion, cela fait qu'elle ne pousse pas celle qui sort pour faire le jet, avec la mesme force qu'elle auroit en descendant librement, comme elle fait quand le vase est large. Et cecy est mesme confirmè par une experience qui montre la mesme difficultè de mouvement en l'air quand il passe par un canal estroit. car si l'on prend une sarbacane de 2 ou 3 pieds de longueur et qui n'aye que 3 ou 4 lignes de creux, l'on

3) E. Torricelli ‘De motu aquarum’ dans le Lib. II (‘De motu projectorum’) de ‘De Motu gravium naturaliter descendentium et projectorum Il. duo’ (dans ‘Opera Geometrica’ de 1644, p. 191): ‘Supponimus. Aquas violentèr erumpentes.... etc. (passage déjà cité dans la note 2 de la p. 28 qui précède). Quelques mois plus tard - voyez la note 4 de la p. 171 qui suit - Huygens constata que la différence est parfois considérable.

[p. 168]

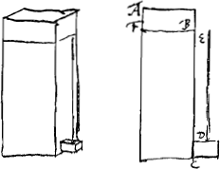
trouvera en soufflant dedans que l'air passe beaucoup plus difficilement que par un morceau de la mesme farbacane qui n'ait que la longueur d'un pouce ou 2.

Mais il y a une autre raison pour la quelle cette figure estroite du vase empesche l'ecoulement de l'eau qui merite sur tout d'estre considerée. Car supposè par exemple que le trou D [Fig. 89] soit la motiè aussi grand que la base du cylindre AC, et que pendant que l'eau s'ecoule par D, on en remette continuellement par en haut en sorte que le cylindre demeure tousjours plein. je dis que l'ecoulement de l'eau ne se fera pas avec la mesme libertè ni par consequent avec la mesme vistesse que si le cylindre estoit beaucoup plus gros.

Car si elle couloit avec autant de vistesse, il faudroit necessairement ou que toute l'eau du cylindre AD descendoit avec la moitiè autant de vitesse que sort l'eau par D, puisque la grosseur du cylindre est double a celle du trou D, la quelle vitesse seroit donc la mesme qu'un corps en acquiert en tombant de la hauteur AE qui est ¼ de AF. ou il faudroit qu'en toutes les hauteurs du cylindre il y eust partie de l'eau qui descendit encore avec plus de vistesse, et partie qui allast plus lentement. Tellement que l'un ou l'autre devroit aussi arriver a l'eau qui est par dessus EG. Mais cette eau et sur tout sa partie plus haute ne peut pas encore avoir acquis d'elle mesme la vitesse qu'un corps acquiert en tombant de la hauteur AE. Il faut donc que celle qui est au dessous de EG aide à luy donner du mouvement en l'attirant apres elle, et par consequent celle sous EG doit presser moins fortement qu'elle ne feroit sans ce retardement, c'est a dire si le vase estoit fort large, parce qu'alors la masse d'eau ne doibt descendre que tres lentement, d'ou il parait donc que le cylindre estroit ne peut pas donner tant d'eau par en bas que le gros, quand les hauteurs et ouvertures sont egales.

Et d'icy peut venir en partie ce que l'experience a fait veoir, que lors qu'on laisse aller l'eau par le trou D¹⁾ sans en remplacer d'autre dans le cylindre AD, elle saute du commencement plus haut que lors qu'on le tient plein, car ne venant point de nouvelle eau en AC a qui celle d'enbas soit obligee de donner mouvement, elle n'en est pas tant retardée.

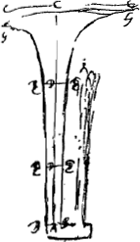
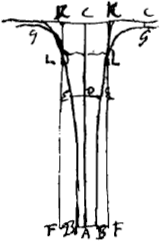
L'on peut mesme determiner par regle quelle largeur il faut dans toutes les differentes hauteurs d'un vase dont la hauteur et l'ouverture d'en bas est donnée, afin que la descente de l'eau se fasse librement²⁾. Car cette ouverture estant par exemple BB [Fig. 90] et la hauteur du vase AC, il faut que la largeur du tuyau vers en haut aille en augmentant suivant la ligne courbe BEEG, qui est une espece d'hyperboloide ayant ses asymptotes ADC et CC et dont la propriété est que comme CD à CA ainsi

1) La Piéce suivante (A § 2) ajoute: ‘débouché subitement’.

2) La Pièce suivante (A § 2) ajoute: ‘quant a ce dernier empeschement’.

[p. 169]

[Fig. 90.]

[Fig. 90 bis.]

le quarrè-quarrè de AB au qu.qu. de DE. Car le tuyau aijant cette figure il arrivera qu'a chaque hauteur EE l'eau aura acquis par sa cheute depuis CC la vistesse requise pour qu'il en passe egale quantitè en temps egaux par la section EE et par BB. dont la demonstration est aisee³⁾.

Car la vistesse acquise en A [Fig. 90 bis] estant a la vistesse acquise en D, en raison sousdouble de la hauteur CA à CD, et d'un autre costè la section EE estant a la section BB comme le quarrè de EE au quarrè de BB, c'est a dire en raison sousdouble du quarrè-quarrè de EE au qu.qu. de BB, ou bien en raison sousdouble de CA à CD. il s'en suit que la vistesse en A est a la vistesse en D comme la section EE est a la section BB, et que par consequent il passera mesme quantitè d'eau en mesme temps par EE et par BB, par la seule vistesse acquise par la cheute CC, sans que la partie plus basse de l'eau attire aucunement la plus haute.

3) La Pièce suivante a, au lieu des cinq derniers mots et de l'alinéa suivant: ‘dont la demonstration est la mesme que donne Torricelli pour prouuer que l'eau en s'escoulant par un trou rond percé dans le fonds du vase forme un corps, qui va en diminuant suivant cette mesme figure donnée au tuyau GEB [la figure fait défaut], car il prouve que comme la vistesse de l'eau acquise en tombant de la hauteur CA est a celle qui s'acquiert en tombant de CD, ainsy la section circulaire EE a l'ouverture BB, d'ou s'ensuit qu'il passera egale quantité d'eau en temps egaux par EE et par BB, et cela par la seule vistesse acquise par la cheute depuis CC, sans que la partie plus basse de l'eau soit obligée d'attirer la plus haute’.
Cette proposition de Torricelli se trouve à la p. 197 de l'ouvrage cité dans la note 3 de la p. 166. Torricelli l'attribue à Castelli. Au début de ‘De Motu aquarum’ il avait déjà fait mention de l'‘Abbate Benedicto Castellio praeceptore meo’. Voir encore sur Castelli la p. 173 qui suit.

[p. 170]

Que si l'on propose un cylindre droit KKFF dont le fonds soit percè d'une ouverture donnee BB, l'on pourra connoistre par le moien de cette ligne courbe jusqu'a quel endroit sa largeur suffit pour laisser a l'eau la descente libre, car ayant descrite la courbe BEG aux asymptotes AC et CK, elle coupera le costè du cylindre KKBB, comme icy en L, et ce sera depuis BB jusqu'en L que sa largeur sera suffisante, le reste estant trop estroit, de sorte que l'eau qui sera depuis L jusqu'en K donnera quelque empeschement a l'escoulement de l'eau, de sorte que suivant cette theorie il y aura tousjours tant soit peu de cet empeschement, de quelque largeur que soit le cylindre droit, parce que la courbe BEG coupera necessairement ses costez.

Le § 2 est tiré des Registres de l'Académie (T. III, p. 111 et suiv.).

§ 2. Du Mercredy 8^e. Oaust 1668.

M^r Hugens a fait plusieurs reflections sur ces experiences [les expériences mentionnées au début du § 1¹⁾]. Il a dit qu'on en pouuoit conclure que la theorie que Torricelli a donnée de l'escoulement des eaux est veritable et que si la pratique ne respond pas tout a fait exactement à la speculation cela ne vient que de quelques circonstances particulieres qui estant bien examinées font descouurir la cause de cette difference²⁾.

De la premiere expérience il a inferé que la largeur du vaisseau ne fait plus rien a la pression sur les parties du fond, au cas de cette expérience, mais que sa force depend seulement de la hauteur de l'eau contenue, puisqu'il est constant que la hauteur estant diminuée l'eau coule moins viste qu'auparauant.

Sur la seconde experience il a dict qu'on en peut conclure que le fond est pressé

1) D'après le p. 110 du T. III des Registres de l'Académie des Sciences on fit le 8 août 1668 les expériences suivantes (après que Picard eut parlé sur ce sujet le 25 juillet et plus tard): ‘Premièrement ayant remply d'eau deux vaisseaux cylindriques d'egale hauteur mais de largeur differente, dont le second estoit percé d'ouuertures egales et les ayant soigneusement entretenus plains d'eau on a trouué, qu'ils rendoient une egale quantité d'eaüe en temps egaux, pourveu neantmoins que ces ouuertures fussent petites en proportion de la largeur des uaisseaux.....
Secondement on a percé d'une egale ouuerture un mesme uaisseau en differents endroicts de son fond; et l'on a trouué qu'il sortoit par ces ouuertures une egale quantité d'eau en temps egaux.
Troisiemement on a obserué que la surface de l'eau qui s'escoule d'un uaisseau cylindrique descend en parties egales de temps par des espaces inegaux qui diminuent en mesme proportion que ceux que parcourt un corps pesant ietté en haut ...’
On voit que dans le § 1 Huygens ne parle que de la première et de la troisième expérience.

2) Comparez le début du § 1 qui précède.

[p. 171]

également en toutes ses parties; et puis qu'il est constant d'ailleurs, que le fond soustient toute la pesanteur de l'eau contenue dans le vase, il s'ensuit que chaque partie du fond est pressée iustement autant qu'elle le seroit par un cylindre d'eau qui auroit cette mesme partie pour base, et la hauteur egale a celle de la profondeur de l'eaüe. Je dis, adiouta t'il, qu'elle est autant pressée, parce que je ne crois pas qu'une partie du fonds soit pressée seulement par le cylindre d'eaüe qui a cette partie pour base. Car asseurement comme ce n'est pas l'eau de ce cylindre qui suit la premiere pour s'escouler quand on ouvre le fond par cet endroict, pendant que le reste de celle qui est contenue dans le vaisseau demeure immobile, mais que de tous costez l'eau s'approche vers l'ouuerture d'en bas, il faut aussy dire que toute l'eau du vase contribue au pressement qui se fait sur chaque partie du fonds, mais que ces forces sont balancées et distribuées d'une telle facon qu'elles viennent toutes a esgaler la force que feroit le poids du cylindre d'eau qui est directement dessus.

Pour representer en quelque facon cette pression de l'eau, et quelles parties s'escoulent successivement l'une apres l'autre, i'ay mis icy le vase BBCC³⁾ percé au fonds en A, par ou l'eau s'escoule pendant qu'on l'entretient tousiours plain, vers laquelle ouuerture l'eau du vase se doit approcher enuiron suiuant l'ordre des espaces que comprennent les lignes courbes que ie suppose de telle nature que chaque bande enfermée de deux de ces lignes a ses largeurs proportionnées aux hauteurs qu'il y a de chaque endroict jusqu'a la surface de l'eau BB. Ainsy la largeur de la bande EDE en D doibt estre a celle en E comme la hauteur GD a FE. Car il est certain qu'a mesure que l'eau commence a s'escouler par A, celle qui est la plus proche de cette ouuerture vient la premiere a remplir sa place, et cela en sorte que ses parties y tendent selon qu'elles sont plus ou moins pressées. De sorte que les premieres courbes aupres du trou A doiuent pour cela estre a peu pres circulaires, et de là peu a peu s'estendre plus uers les costez que vers en haut comme elles sont icy marquées.

Or suiuant ce mouuement des parties de l'eau vers A elles doiuent aussy faire impression a cet endroit puisque le pressement n'est autre chose que l'effort d'un corps a succeder a la place d'un autre.

Pour ce qui est de la 3^e. experience, il a dit que pour la demonstrer comme toutes les autres propositions du traitté de Toricelli, il faut supposer un effect de la nature, qui ne s'estant pû jusqu'icy demonstrer par raison, mais seulement prouuer par experience, doit estre pris pour principe en cette matiere⁴⁾. C'est que ....... etc. à peu près comme dans la Pièce du § 1. Le texte des premiers alinéas qui suivent diffère consi-

3) La figure fait défaut. Voyez la p. 93 qui précède.

4) Quelques mois plus tard - nous l'avons dit aussi dans la note 3 de la p. 166 -, plus précisément le 16 février 1669, Huygens crut constater que la loi de Torricelli est loin d'être exacte. Comparez la note 4 de la p. 121 qui précède et le § 4 à la p. 173 qui suit.

[p. 172]

dérablement de celui des alinéas suivants du § 1, mais le sens est le même. Viennent ensuite plusieurs alinéas presque identiques avec ceux du § 1; les variantes sont fort peu importantes; voir cependant les notes des p. 168 et 169.

Le Registre ajoute: ‘On a resolu de traitter dans la prochaine assemblée des principes generaux du mouuement des eaux. et de continuer aussy a examiner le mouvement des eaux qui s'écoulent d'un reservoir percé par le fond a quoy on a prié Mons.^r Picard de penser’. Dans la séance du 28 août 1668¹⁾ Picard avança en effet ‘plusieurs propositions sur ce subject’, lesquelles sont rapportées dans le Registre.

Il est dit à la fin de ce dernier rapport: ‘Le mesme jour M^r de Roberval a parlé des principes generaux du mouuement des eaux’.

On fit encore quelques expériences sur l'écoulement en septembre de la même année, et l'on commença la discussion sur la ‘force de l'eau courante’ ou ‘force de l'eau a mouuoir’, qui conduisit aux expériences de 1669, rapportées dans la Pièce V qui précède.

1) Le 28 août 1668 est désigné par ‘mercredy’. Or, ce jour était un mardi. Il y a donc peut-être une erreur de date.

§ 3²⁾.

Aqua ex imo tubo erumpens habet celeritatem aequalem ei quam plumbum quod decidit ex altitudine quantam habet aquae superficies supra aperturam. quia ad eandem superficiei altitudinem exibit nisi quod ab aere nonnihil impediatur [voyez cependant le § suivant].

Plumbum vero ex altitudine ped. 15 et 1 poll. decidens tempore unius scrupuli secundi²⁾ celeritatem eam acquirit qua bis tantum spatium hoc est 30 ped. 2 poll. uno secundo scrupulo percurreret motu aequabili. Ergo et aqua pressa altitudine 15 ped. 1 poll. ea celeritate erumpit qua 30 ped. 2 poll. uno secundo conficeret. Ergo per foramen quadratum pollicare exeunt, in ista altitudine, 362 poll. cubi tempore 1″. Ergo, tempore 1′, sexagies tot pollices cubi hoc est 21720 poll. Ergo 1 horâ pollices 1303200. Est autem foramen quadratum pollicare ad foramen rotundum diametri pollicaris ut 14 ad 11. Ergo per foramen hoc rotundum exibunt pollices 1023943 in hora. hoc est pedes cubi 592½. Et in 24 horis pedes cubi 14220. Et per foramen rotundum cujus diameter 1 linea sive 1/12 pollicis exibunt in 24 horis pedes cubi 98 5/7, hoc est proximè 100, premente semper 15 pedum et 1 pollicis altitudine.

Quod autem vocant un muid d'eau, 8 pedibus cubis aestimatur. Ergo isti pedes cubi 98 5/7 faciunt 12 muids et ⅓.

Quod autem dicunt une ligne d'eau, à fonte promanans, id censetur implere un muid, sive 8 pedes cubos, spatio 24 horarum.

Pressio 14 pedum hinc invenitur per foramen linearis diametri exprimere proxime 12 muids in 24 horis.

Si scire velim quantum per idem foramen eodem tempore expressura fit altitudo 20 pedum, facio ut 14 ad 20 ita 12 modij ad 17 1/7, quo ducto in 12, et ex producto extracta radice fit proximè 14⅓ modij, qui exibunt.

2) Manuscrit D, p. 139. La p. 118 est datée 1669 et la p. 145 1 Febr. 1669.

2) Comparez la Pièce II à la p. 96 qui précède.

[p. 173]

§ 4³⁾. 16 fevr. 1669.

Experience faite avec un tuyau de fer blanc ayant de hauteur 35 pouces Paris. diametre de la base 5 pouc. 9 lignes. Il y avoit au fond un trou rond du diametre de 4 lignes.

Estant rempli d'eau et placè perpendiculairement se vuidoit en 2 min. 57 sec. Estant entretenu plain vuidoit autant d'eau, qu'il en faloit pour le remplir, en 1 min. 35 sec.

Huygens calcule que le ‘contenu du cilindre’ est de ‘909¼ pouc. cubes’.

Pour scavoir en combien de temps se devoit vuider autant d'eau qu'est le contenu dudit cilindre par ledit trou de 4 lignes, estant le cylindre entretenu plein: suivant la vitesse prise de la cheute des corps pesants, de 15 pd. 1 pouc. en une seconde [pied de Paris].

Nous supprimons le calcul qui donne 65⅖ secondes.

On peut supputer cela plus facilement, de ce que comme le trou du fond est a tout le fond ainsi le temps de la cheute d'un corps quitomberoit de la hauteur qu'a l'eau dans le vase, au temps de l'ecoulement total; dont la moitiè est le temps de l'ecoulement d'autant d'eau en tenant le vase plein⁴⁾. Ce temps icy selon ce calcul ne se trouue que de 1′ 5⅖″, et par l'experience il est trouuè de 1′, 35″, qui sont presque comme 2 à 3. Ce qui montre que toute l'eau qui sort par le trou du vase n'a pas autant de vitesse qu'auroit un corps en tombant de la surface de l'eau, mais seulement une partie la quelle jalit a la hauteur de la surface, ce qui n'estoit pas facile a deviner⁵⁾.

On trouve déjà plusieurs propositions et corollaires sur la quantité d'eau sortant en un temps donné par une ouverture donnée dans les ‘Hydraulica, pneumatica, etc.’, faisant partie des ‘Cogitata physicomathematica’ de 1644 de Mersenne (cités aussi aux p. 87 et 142 qui précèdent). Mersenne cite (p. 55) ‘Castellanus tract. de aqua currente’. Il s'agit de Benedetto Castelli (1577-1643) ‘Della misura delle acque correnti’, Roma 1628. Comparez sur Castelli la note 3 de la p. 169 qui précède.

La f. 256v. du T. VII des Registres de l'Académie nous apprend que ‘M^r. Roemer a rendu compte le 26. d'Aoust 1679 des experiences qu'il a fait a Versailles en presence de M^r. Picard par ordre de Monseigneur Colbert. Il a trouué que les trous de 8. et 12. lignes fournissaient plus d'eau que de petites ouuertures de 3. ou 4. lignes, car on a trouué que les petites ouuertures fournissoient beaucoup moins d'eau que la demonstration de M^r. Hugens n'exige, mais a l'egard des grandes ouuertures la quantité d'eau qui en sortoit s'accordoit parfaitement avec la proportion de M^r. Hugens. Il a encore trouué que dans les grandes et petites ouuertures, la quantité d'eau qui en sortoit estoit tousjours proportionnelle au sous-double des hauteurs. Etc.’

Ce qui précède fait voir que Huygens savait fort bien que la règle énoncée sur la quantité d'eau qui s'écoule en un temps donné est parfois loin d'être exacte. Comparez les p. 167-168.

3) Manuscrit D, p. 159. Huygens fait mention de l'expérience du § 4 dans le discours du 29 mai 1669 (p. 137 qui précède).

4) Cette règle correspond à la loi de Torricelli. Elle suppose qu'il n'y a pas de contraction du jet.

5) Il doit y avoir eu contraction du jet; comparez la p. 91 de l'Avertissement.

[p. 174]

[Fig. 92.]

[Fig. 91.]

B¹⁾. Aquam saliendo ascendere ad altitudinem superficiei ejus quae est in vase²⁾.

Vires centrifugas esse ut distantias à centro in partibus aquae ejusdem tubi horizontaliter conversi.

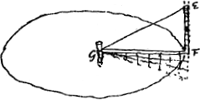
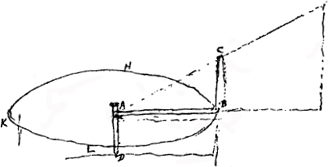
AB [Fig. 91] canalis circa axem AD rotatus in plano horizonti parallelo. Ad B est apertura, unde aqua pressa, per vim centrifugam ejus quae canalem AB replet exilit ad altitudinem BC aequalem ½ AB. suppletur autem aqua per orificium in A, quod in ipsa superficie stagnantis aquae situm pono.

Quaeritur jam qua celeritate extremum punctum B converti debeat comparando eam ad celeritatem casus ex CB. Dico huic ipsi aequalem requiri. Cum enim aqua continuè saliat ad altitudinem BC, id fieri non potest nisi pressio aquae in extremo tubo B aequalis sit pressioni aquae in tubo EF [Fig. 92] cujus altitudo aequalis BC³⁾.

1) Manuscrit G. f. 126 v. et 127r. Les f. 123 et 127v. portent respectivement les dates du 1 septembre et du 1 octobre 1691.

2) Suivant le principe (p. 166, § 1) que Huygens emprunte à Torricelli.

3) En formules: la pression en B résultant de la force centrifuge est (ω = vitesse angulaire, S = section droite du tube, δ = densité de l'eau, R = AB) ou bien p = ½ S δ V², V étant la vitesse linéaire de l'extrémité B. Le poids de la colonne d'eau EF(EF = ½ R) est p′ = = ½ S δ g R (g = accélération de la pesanteur). On a donc p = p′ lorsque , vitesse qui correspond à une chute libre suivant EF.

[p. 175]

Quis autem labor est tubum AB convertentis, nisi ut singulis conversionibus tantundem aquae atque eo tempore exilit ex B, celeritatem imprimat eam quae est puncti B, circumferentiam BHKL percurrentis [Fig. 91]. quare aequè celer est motus aquae ad B exilientis, quam in circumferentia BHKL circumvolutae.

Videndum amplius. Considerandum quod, si talis celeritas esset puncti B, aqua sic exiliens parabolas describeret angulo 45^o surgentes, ac propterea, praeter celeritatem qua adscenditur ad BC, etiam lateralem motum aquae imprimi oporteret, cujus opera, tempore ascensus per BC, conficeret spatium laterale duplum ipsius BC. Itaque ad convertendum tubum AB salientem, ut extremum B feratur in circumferentia tanta celeritate quanta acquiritur cadendo ex CB, duplo plus virium requiretur quam si singulis aquae partibus eadem haec celeritas imprimenda esset. Sed quandiu quaerimus celeritatem puncti B, non adhuc scimus quali angulo parabolae ascendant, etsi altitudinem earum sciamus esse BC. qualescunque autem sint istae parabolae, sequitur non utiliter⁴⁾ hujus modi machinam adhiberi extollendae aquae.

Si tubus GFE [Fig. 92] habeat partem perpendiculariter erectam FE dimidiae FG aequalem et revolutione sua circa G sustineat aquam in GFE (aperto nempe tubo circa G) jam ostendi potest vis centrifuga in F aequalis esse gravitati. Ergo et exiliente aqua ad altitudinem BC ∞ FE, vis centrifuga erit aequalis gravitati.

Meum autem theorema dicit vim centrifugam in F aequalem esse gravitati quando F fertur in circumferentia celeritate quanta acquiritur cadendo ex EF⁵⁾. Ergo, si verum est theorema meum, necesse est exiliente aqua ad altitudinem BC ∞ ½BA, celeritatem B in circumferentia aequalem esse celeritati ex casu per CB. Est autem verum theorema, ergo &c. Sed si demonstranda hinc sit theorematis mei veritas⁶⁾, oportet probare aquâ exiliente per BC, hoc est sustentatâ in FE, hoc est quando vis centrifuga in B aequatur gravitati, tunc celeritatem B in circumferentia aequari celeritati ex casu per CB.

An posset probari qualicunque celeritate gyretur tubus AB, semper ab exiliente aqua parabolas describi quae ascendant angulo 45^o. quod procul dubio verum est, sed quomodo demonstrabitur [?]⁷⁾. Hoc satis esset.

4) A cause du trop grand ‘labor tubum convertentis’.

5) De Vi Centrifuga, Prop. V (T. XVI, p. 275, p. 316, ou T. XVIII, p. 366).

6) C.à.d. si l'on veut démontrer expérimentalement par l'expérience du jet d'eau la vérité du théorème sur la force centrifuge.

7) Lorsque EF (comparez la note 3) n'est pas égale à ½ R, mais a une longueur quelconque h, on aura p = p′ pour ; c.àd. en vertu de la force centrifuge l'eau dans la partie verticale du tube peut être maintenue à une hauteur . Or, suivant le principe de Torricelli l'eau qui remplit un tube de hauteur h s'écoule avec une vitesse , c.à.d. = V. On peut en conclure que, lorsque la partie verticale du tube fait défaut, l'eau n'étant plus tenue en équilibre, sortira du tube horizontal (recourbé vers le haut à son extrémité) avec cette même vitesse verticale V. Le jet s'élancera donc sous un angle de 45^o.
Mais ceci ne peut guère être considéré comme une démonstration en règle. Dans la pratique on constatera sans doute de notables écarts.

[p. 176]

En 1686 avait paru à Paris le ‘Traité du mouvement des eaux et des autres corps fluides’ par Mariotte (éd. de la Hire). Daniel Bernoulli dans son ‘Hydrodynamica’ de 1638 (le mot hydrodynamica désigne à la fois l'hydrostatique et l'hydrodynamique, cette dernière étant appelée hydraulica) donne dans la Sectio Prima un aperçu historique du sujet⁸⁾.

Il dit e.a. (§ 18) ‘Jam vero tandem principiorum, quorum toties mentionem fecimus, ratio reddenda est. Praecipuum est conservatio virium vivarum, seu, ut ego loquor, aequalitas inter descensum actualem ascensumque potentialem’. § 19 ‘malui ... hanc hypothesin verbis Hugenianis .... accommodare, eamque nomine aequalitatis inter descensum actualem ascensumque potentialem insignire [Huygens toutefois ne se servait point des expressions “actuel” et “potentiel”; comparez les notes 4 de la p. 341 et 4 de la p. 349 du T. XVI, et la p. 469 du T. XVIII] quam altero conservationis virium vivarum [comparez la p. 466 du T. XVIII] ... Mihi quidem in tota doctrina Leibnitiana de viribus vivis nihil esse videtur, de quo non omnes, suo tamen loquendi modo, conveniunt’.

Il jugeait oiseuse la ‘querelle des forces vives’, dont il est question dans la note 2 de la p. 162 qui précède.

8) On peut consulter aussi la ‘Raccolta d'Autori che trattano del Moto dell' Acque’ (9 vol. 2 ième éd. Firenze, nella stamperia di sua Altezza Reale, 1765-1774).