Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 51]

VII.
Spartostatique.
[1667 et 1688-1691]

[Fig. 23.]

[Fig. 24.]

¹⁾²⁾

1) La partie A de la Pièce VII - la division en §§ est de nous, comme partout ailleurs - est empruntée aux p. 196-205 du Manuscrit C, lesquelles contiennent encore plusieurs autres figures dans le genre des Fig. 23 et 24, ainsi que des calculs plus amples. Les p. 194 et 203 du Manuscrit portent respectivement les dates du 15 août et du 5 septembre 1667, la p. 231 celle du 25 février 1668. - Les §§ 4-6 sont reproduits dans l'écriture de Huygens aux f. 118 et 119 des Chartae mechanicae. La date ‘5 Sept. 1667’ - voir le § 5 du texte - s'y trouve au § 4. Nous n'indiquons pas les variantes des §§ 4 et 5.
Du Hamel dit dans son ‘Historia’ (p. 40) que Huygens traita le problème de l'équilibre des cordes à l'Académie en 1667 et le ‘scripto exposuit’: comparez la note 4 de la p. 53 qui suit.

2) Le noeud des trois cordes PE, QE, SE ayant été transporté de E en C, Huygens écrit l'équation qui exprime que la somme des travaux est nulle; p, q et s représentent évidemment les tensions des cordes. Comparez sur le principe des déplacements virtuels la p. 16 qui précède.

[p. 52]

³⁾

d'où l'on peut tirer les tensions lorsque les angles sont donnés.

[Fig. 25.]

3) Ici les tensions des quatre cordes sont représentées par P, R, S, T ou p, r, s, t. Huygens considère quatre déplacements virtuels respectivement perpendiculaires aux quatre cordes, ce qui donne 4 équations.

[p. 53]

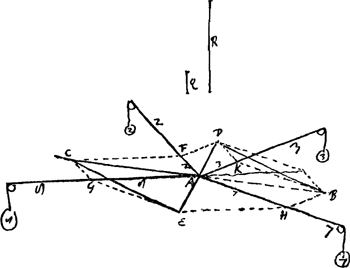
VII, A. § 3. Datis quatuor ponderibus quorum chordae A7, A3, A2, A8. communi nodo ad A connectuntur [Fig. 25]. Invenire quales angulos inter se chordae illae efficere debeant. Unus angulus A7, A3 sumatur ad lubitum, et in chordis A7, A3 sumantur distantiae AH, AK quae sint inter se ut pondera 7 ad 3. et compleatur parallelogrammum KH. cujus diameter BA producatur versus A et sumatur in ea AC aequalis AB. Porro ut pondus 3 ad 2 ita sit AK ad rectam Q et ut pondus 2 ad pondus 8 ita sit Q ad R. Et super recta AC fiat triangulum AFC cujus latus AF ∞ Q; et FC ∞ R. (Quod si Q + R sint minores quam AC, indicio est angulum 7A3 majorem sumi debuisse). Deinde ducatur AG parallela FC. Eruntque AF, AG chordae ponderum 2 et 8.

Si enim essent chordae tres duntaxat A7, A3, AC trahereturque chorda AC pondere quodam quod ad pondus 7 esset ut AB vel AC ad AH. constat fore aequilibrium manente nodo in A. Atqui tantundem efficiunt pondera 2 et 3 trahentia chordas AF, AG, atque pondus illud trahens AC. Ergo et pondera 2 et 3 trahentia chordas AF, AG aequilibrium facient cum ponderibus 7, 3, trahentibus chordas AH, AK.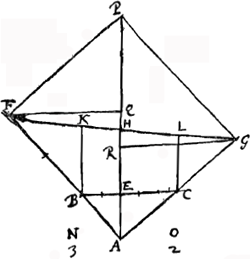

[Fig. 26.]

VII, A. § 4⁴⁾. Si punctum A [Fig. 26] trahatur per fila duo AB, AC, angulum facientia, sintque potentiae trahentes ut filorum ipsorum AB, AC longitudines multiplices secundum numeros datos N et O. ac jungatur BC et dividatur in E, ut reciproce sit CE ad EB sicut numerus N ad O, et jungatur AE, dico attractioni filorum AB, AC per dictas potentias aequipollere attractionem per filum AE, à potentia quae sit ut longitudo AE multiplex secundum numerum aequalem utrisque N et O.

Producantur enim AB, AC et sit AF multiplex AB secundum numerum N. Et AG multiplex AC secundum numerum O. Et juncta FG, occurrat ei AE producta in H; sintque BK, CL parallelae AH.

4) Le texte des §§ 4, 5 et 6 a été publié dans la version des ‘Chartae mechanicae’ (comparez la note 1 de la p. 56) dans les ‘Divers Ouvrages de Math. et de Phys. par MM. de l'Ac. R.d. Sciences’ de 1693, p. 317-319) sous le titre ‘De potentiis fila funesve trahentibus’. Le texte des ‘Divers Ouvrages’ s'accorde avec celui des Registres de l'Académie des Sciences, T. II, p. 142-147 (comparez le deuxième alinéa de la note 1 de la p. 51).

[p. 54]

Est ergo FH ad HK ut FA ad AB, hoc est, ut numerus N ad unitatem. HK vero ad HL ut BE ad EC, hoc est, ut numerus O ad numerum N. Ergo, in proportione perturbata, erit FH ad HL ut numerus O ad unitatem, hoc est, ut GA ad AC, sive ut GH ad HL. Ergo cum ratio FH ad HL sit eadem, quae GH ad HL, erit FH aequalis HG.

Sit jam AH continuata in P ut sint aequales AH, AP, et jungantur PF, PG. Eritque FAGP parallelogrammum ad cujus diametrum PA ducantur FQ, GR parallelae BC. Et manifestum est fieri triangula similia et aequalia FPQ, GAR, quorum latera inter se aequalia PQ, RA. Est autem AE ad AQ ut AB ad AF, hoc est, ut unitas ad numerum N. Eadem vero AE ad AR ut AC ad AG, hoc est ut unitas ad numerum O. Ergo AE ad utramque simul AQ, AR sive AQ, AP ut unitas ad utrumque numerum N et O.

Cum ergo potentiae fila AB, AC trahentes sint ut AF, AG, ijsque aequipolleat attractio per filum AE in potentia quae sit ut AP, manifesta est propositionis veritas.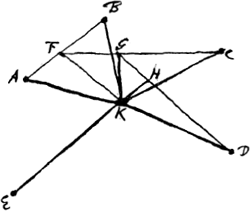

[Fig. 27.]

VII, A. § 5. 5 Sept. 1667.

Datis positione punctis quotlibet, sive in eodem plano fuerint sive non: si à puncto, quod eorum commune est gravitatis centrum, ad unumquodque datorum fila extendantur, eaque singula trahantur a potentijs, quae sint inter se ut filorum longitudines; fiet equilibrium manente nodo communi in dicto gravitatis centro.

Sint data positione puncta A, B, C, D, E [Fig. 27], quae vel in eodem plano vel aliter utcumque collocata concipiantur. Attributa autem singulis aequali gravitate, constat commune eorum gravitatis centrum inveniri hoc modo. Nempe jungantur duo quaelibet datorum punctorum recta AB; qua bifariam secta in F, erit hoc centrum gravitatis punctorum A, B. Ducatur deinde ad punctum tertium recta FC, quae sece-

[p. 55]

tur in G, ut CG sit dupla GF, et erit G centrum gravitatis punctorum trium A, B, C. Rursus ducatur GD ad punctum quartum, seceturque in H ut DH sit tripla HG, et fiet H centrum gravitatis punctorum quatuor A B C D. Denique ducta HE ad punctum quintum E, secetur ea in K ut sit EK quadrupla KH; eritque K centrum gravitatis punctorum quinque A B C D E. similique ratione quotlibet punctorum centrum gravitatis inveniri liquet.

Porro extendendo fila a puncto K ad A, B, C, D, E, quae trahantur a potentijs quae sint inter se ut ipsae longitudines KA, KB, KC, KD, KE; dico fieri aequilibrium manente nodo communi in K.

Ducantur enim a centris gravitatis inventis F, G, H, ad centrum gravitatis omnium punctorum K, lineae rectae FK, GK, HK. Itaque constat filis AK, BK punctum K trahentibus cum potentijs quae sunt ut longitudines horum filorum, aequipollere potentiam trahentem filum KF, quae sit ut dupla KF. Rursus vero filo KF trahenti cum potentia quae sit ut dupla KF, et filo KC trahenti cum potentia quae sit ut longitudo KC, his inquam duobus aequipollet filum KG tractum a potentia quae sit ut tripla KG, per propositionem praecedentem. Et similiter filo KG ita tracto, et filo KD à potentia quae sit ut longitudo KD, aequipollet filum KH tractum à potentia quae sit ut quadrupla KH. Ergo filis KA, KB, KC, KD punctum K trahentibus, aequipollet filum KH tractum a potentia quae sit ut quadrupla KH, hoc est, ut KH multiplex secundum numerum punctorum A, B, C, D. Atqui filo HK in directum opponitur filum KE, tractum a potentia quae est ut longitudo KE, id est, ut quadrupla KH. Ergo cum filis KH et KE cum potentia aequali trahentibus ac directe sibi invicem oppositis, necessario punctum K locum suum servaturum sit, sequitur etiam filis KA, KB, KC, KD uti dictum est trahentibus, et ex alia parte filo KE, nodum K restare immotum. quod erat demonstrandum.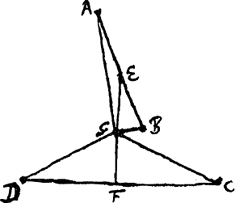

[Fig. 28.]

Possunt autem et binorum quorumque punctorum centra gravitatis primum inveniri, et per haec deinceps contra quaternorum, et per haec octonorum, prout numerus punctorum patietur. qua ratione simplicior plerumque fit demonstratio, ac praesertim si punctorum numerus sit pariter par. ut si quatuor data fuerint A, B, C, D [Fig. 28], sive in eodem plano, sive non: junctis AB, DC, divisisque bifariam in E, F, erunt haec centra gravitatis punctorum A, B et C, D, et juncta deinde EF divisaque bifariam in G, erit hoc centrum gravitatis commune

[p. 56]

omnium punctorum A, B, C, D. Quod si jam nodus G trahatur per fila GA, GB, GC, GD cum potentijs quae sint inter se ut hae ipsae longitudines, dico fieri aequilibrium.

Constat enim filis GA, GB aequipollere filum GE tractum à potentia quae fit ut dupla GE. Filis vero GC, GD aequipollere filum GF, tractum a potentia quae sit ut dupla GF. Cum ergo GE, GF aequales sint unamque lineam rectam efficiant, eodem modo punctum G trahitur ac si traheretur a potentijs aequalibus per fila GE, GF. Unde immotum manere necesse est. quod erat demonstrandum.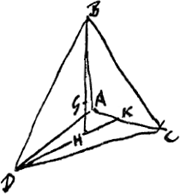

[Fig. 29.]

VII, A. § 6. Constat vero, si puncta A, B, C, D [Fig. 29] non sint in eodem plano fore G centrum gravitatis pyramidis, cujus anguli ipsa puncta A, B, C, D. quoniam in omni pyramide centrum gravitatis solidi est idem quoque centrum gravitatis quatuor punctorum angularium. Sit enim pyramis A, B, C, D. et sit H centrum gravitatis trianguli baseos DAC, quod idem quoque patet esse centrum gravitatis trium punctorum D, A, C; nam producta DH, secat latus AC bisariam unde K centrum gravitatis punctorum AC. ipsa vero DK dividitur in H, ut DH sit dupla HK. unde liquet punctum H esse centrum gravitatis punctorum A, B, C. Jam vero HB dividitur a centro gravitatis pyramidis G ut sit BG ad GH ut 3 ad 1. unde constat punctum G esse quoque centrum gravitatis quatuor punctorum angularium A, B, C, D¹⁾.

1) Dans les ‘Chartae mechanicae’ - comparez la note 1 de la p. 51 - le texte correspondant à ce que nous appelons ici le § 6 est le suivant: Constat vero, si puncta A, B, C, D non sint in eodem piano, fore G centrum gravitatis pyramidis cujus anguli haec ipsa quatuor puncta. Cum in omni pyramide idem sit centrum gravitatis ipsius solidi, et quatuor punctorum angularium, ut ostendere facillimum est. Et hinc patet veritas theorematis Robervalliani, quod si a centro gravitatis pyramidis fila tendantur ad 4 angulos, quae trahantur a potentijs quae sint inter se ut filorum ipsorum longitudines, fieri aequilibrium manente nodo in dicto gravitatis centro.
Ce texte s'accorde exactement avec celui qu'on trouve à la p. 147 du T. II des Registres de l'Académie des Sciences de Paris. - La Pièce entière (nos §§4-6) y occupe les p. 142-147.
Quant au ‘theorema Robervallianum’, on trouve en effet aux p. 85-113 du T. II des Registres un traité de Roberval ‘du centre de grauité’, contenant douze propositions et leurs démonstrations, dont la onzième est la suivante: ‘Tout ce que dessus estant supposé comme démonstré, je dis que s'il y a quatre puissances aux quatre poincts A, B, C, D, qui tirent par les quatre lignes qui aboutissent au centre, I, qui soient autant de Cordes IA, IB, IC, ID, ces quatre puissances estant supposées estre en equilibre, elles seront proportionnées entre elles comme leur quatre Cordes’. D'après la p. 162 du même Tome, ce traité fut lu par Roberval le 27 avril 1667.

[p. 57]

[Fig. 30.]

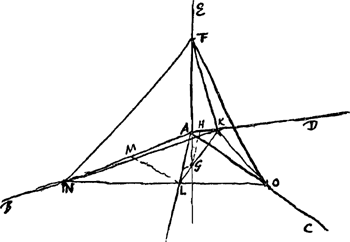
VII, A. § 7. Datis quatuor rectis ab uno puncto A eductis ut AB, AC, AD, AE [Fig. 30], quaeque ita sint positae ut plano quovis per A ducto non sint omnes ad partem ejus eandem nec tres in ipso plano; Invenire pyramidem FNOK, cujus anguli sint in praedictis lineis rectis, centrum vero gravitatis in puncto A.

Intelligatur una datarum linearum ut EA produci, sumtaque in ea AF ad arbitrium, ponatur ex altera parte AG aequalis trienti AF. Oportet igitur ducere planum per punctum G, quod occurrens rectis AC, AD, AB in punctis O, K, N, faciat ut G sit centrum gravitatis trianguli OKN. Sic enim pyramis quaesita erit FOKN, cujus centrum gravitatis punctum A; quoniam FG, quae a vertice ad centrum gravitatis baseos NKO ducta est, dividitur in A ut FA sit tripla AG. Ut igitur inveniatur positio plani istius per. punctum G ducendi intelligatur planum duci per rectas AK, AG, itemque aliud per AN, AO, sitque eorum intersectio recta AL. Jam ducatur GH parallela AL, occurratque rectae AD in H, et sumatur AK tripla AH; et ducatur KG, quae producta occurrat ipsi AL in L. Ergo et KL erit tripla GL. Jam in plano ANO, ducatur LM parallela AO, occurratque ipsi AB in M, et sumatur AN dupla AM, et ducatur NLO, occurrens rectae AC in O. Erit jam NO dupla quoque NL. sicut NA dupla est NM. Itaque G erit centrum gravitatis trianguli NKO, cum KL dividat basin NO bisariam sitque secta in G ut KG sit dupla GL. Ergo junctis OF, OK, KN, KF, NF pyramis NFOK erit quae quaerebatur.

[p. 58]

[Fig. 31.]

[Fig. 31 bis.]

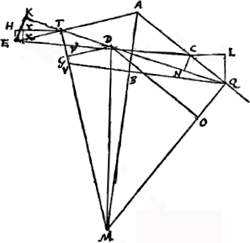
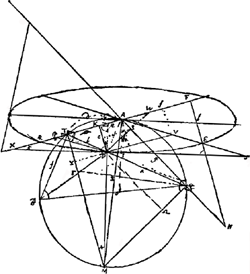
VII, B. § 1¹⁾. 20 Dec. 1688. Theorema: Si fuerint in plano, ad horizontale planum erecto, duae lineae rectae AE, AQ [Fig. 31] a puncto A deorsum tendentes, intraque angulum ab ipsis comprehensum aptetur linea recta TQ ita posita ut quae ex adsumto in ea puncto D ad perpendiculum descendit tendat ad punctum M in quo conveniunt quae a lineae aptatae terminis T, Q perpendiculares ducuntur in rectas dictum angulum efficientes. Punctum D in linea aptata adsumptum inferiore loco invenietur quam alio quovis positu ejusdem lineae intra eundem angulum.

1) Les §§ 1-6 de la partie B de la Pièce VII sont empruntées aux p. 8-11 du Manuscrit G. Il s'agit dans le § 1 de déterminer la position d'équilibre de la barre inflexible et impondérable TDQ, portant un poids en D et pouvant glisser en T et Q sur les droites AT et AQ se trouvant dans un même plan vertical. Huygens n'ignore pas que le lieu des points D est une ellipse; c'est ce qu'indiquent trois figures des p. 6 et 7 du Manuscrit, dont nous reproduisons la dernière [Fig. 31 bis]. Nous ne reproduisons pas les considérations géométriques se rapportant à ces figures. Il s'agit évidemment de déterminer la position du point le plus bas de cette ellipse, mais nous ne voyons pas que les équations écrites conduisent à ce but. Comme on voit, Huygens a ensuite résolu le problème sans parler de l'ellipse. L'intersection des perpendiculaires TM et QM donne le centre instantané de rotation (comparez la note 4 de la p. 401 du T. XVIII); la tangente à la courbe décrite p.e. par le point D attaché à la barre est donc perpendiculaire à MD, et comme cette tangente doit être horizontale, il faut que la droite MD soit verticale.
Huygens s'était occupé de ce problème déjà en 1646; voir sa lettre à Mersenne (p. 40-44 du T. I); consultez aussi la note 1 de la p. 35 du T. I. Mais en 1646 il n'avait considéré que le point milieu de la barre mobile; il avait réussi à prouver que ce point-là décrit une ellipse. Comme en 1688, c'était en réalité de spartostatique qu'il s'agissait.

[p. 59]

Aptetur enim recta ipsi TQ aequalis alio positu, sitque CE. Et ut QT divisa est puncto D ita dividatur CE puncto F. Sit autem punctum C illud quod versus A ascendit, E vero quod ex T descendit, nam si E non descendat ascendente C jam manifestum erit punctum F altius esse quam D. Dico autem et descendente E, punctum F altius esse puncto D.

Sint enim CN, EK perpendiculares in QT qua opus productam. Quia autem anguli CQN, ETK singuli minores recto, cadet necessario punctum N inter QT et K extra. Agantur porro QL, EH parallelae DM, ijsque occurrant ad angulos rectos CL, TH. Est ergo QL mensura ascensus puncti Q in C translati, et HE mensura descensus puncti T translati in E. Sint etiam DO, DG perpendiculares rectis QM, TM. Et jungatur AM quam secet in B ad rectos angulos QV occurrens rectae TM in V. Ac denique sumpta TX in recta AE aequali CQ cadat XY perpendiculum in TH. Quia igitur CQ parallela est DO, et QL parallela DM, erit angulus CQL aequalis MDO, ideoque et angulus QCL aequalis DMO et triangulum CLQ simile MOD. Simili ratione quia TE parallela DG, et EH parallela DM, erit angulus TEH aequalis MDG, ideoque et angulus ETH aequalis DMG et triangulum TEH sive TXY simile MDG. Sicut igitur LQ ad QC ita OD ad DM, et sicut QC sive huic aequalis TX ad XY ita DM ad DG. Ergo ex aequo sicut LQ ad XY ita OD ad DG. Quia itaque ratio LQ ad HE componitur ex ratione LQ ad XY, et ex XY ad HE, seu XT ad TE; componitur eadem ratio LQ ad HE ex ratione DO ad DG et ex TX seu CQ ad TE. Sed ratio haec CQ ad TE major est, ut postea ostendetur, ratione QM ad MT. Ergo ratio LQ ad HE major erit quam composita ex DO ad DG, et ex QM ad MT. Ex his vero componitur ratio trianguli MDQ ad triangulum MDT, estque horum triangulorum ratio ea quae QD ad DT. Ergo ratio LQ ad HE major erit quam QD ad DT. Transposita itaque recta QT in CE, major est ratio ascensus termini Q, qui est QL, ad descensum termini T qui est HE, quam QD ad DT unde constat punctum D, quod jam est in F, altius factum esse, quia nempe in eadem qua prius altitudine mansisset si dictus ascensus ad descensum eandem rationem habuisset quam CD ad DT. Semper autem ascensus ad descensum ratio major esse probatur.

Quod autem dictum est rationem CQ ad TE majorem esse quam QM ad MT, id sic ostenditur. Quia puncta TAQM sunt in circuli circumferentia erunt aequales anguli AQT, AMT, ideoque triangula rectangula similia QNC, MBV. Eademque ratione anguli aequales erunt AMQ, ATQ, hoc est ETK, quam ob rem et triangula rectangula similia erunt MBQ, TKE. Sicut igitur MV ad MB ita CQ ad QN, et sicut

[p. 60]

MB ad MQ ita KT ad TE. Quod si jam QN, KT aequales essent, colligeretur ex aequo esse ut MV ad MQ ita CQ ad ET. Sed KT minor est quam QN. Nam quia CE aequalis TQ, CE vero major quam NK, erit et TQ major quam NK, et ablata communi NT fiet KT minor quam NQ. Itaque ratio CQ ad ET major erit quam MV ad MQ. Est autem ut MV ad MQ ita MQ ad MT, propter similia ∆^la VMQ, QMT quippe angulum communem ad M habentia cum praeterea angulus BQM seu BAQ sit aequalis MTQ eo quod puncta AQMT sint in circuli circumferentia. Itaque apparet rationem CQ ad TE majorem quoque esse quam MQ ad MT. quod probandum supererat.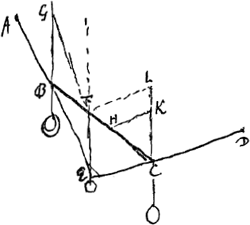

[Fig. 32.]

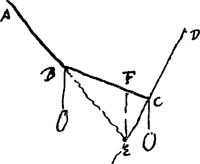
VII, B. § 2. Ex Fune ABCD suffixo in A et D [Fig. 32] pendeant alligata pondera in B et C. Dico si ex puncto E quo conveniunt productae AB, DC, ducatur horizonti perpendicularis EF, eam secare BC, ut sit BF ad FC sicut gravitas in C ad gravitatem in B.

Perficiantur enim parallelogrammata EFGB, EFLC, et sumta CH aequali BF, ducatur rectae CD parallela HK, quae occurrat rectae CL in K. Est igitur gravitas in B ad potentiam attrahentem punctum B versus C, sicut GB ad BF, per praecedentem. Eadem vero est potentia attrahens B versus C, ei qua C versus B attrahitur, quippe cujus utriusque mensura est tensio funis BC¹⁾. Estque potentia haec qua C ad B trahitur ad gravitatem C suspensam, sicut HC ad CK, ex praecedenti. hoc est sicut BF ad CK. Erit igitur ex aequo gravitas ex B ad gravitatem in C sicut GB ad KC, hoc est sicut LC ad KC, hoc est, sicut FC ad CH sive ut FC ad FB, quod erat demonstrandum²⁾.

Quod aequalia non possunt servare locum, si perpendicularis ab intersectione E non

1) En marge: in altero casu, pellens B versus C ei qua C pellitur versus B, quippe cum nec B pellat C, nec C pellat B.

2) En 1646 (voir la note 1 de la p. 58) Huygens n'avait démontré cette proposition que pour le cas où les poids suspendus en B et C sont égaux.

[p. 61]

[Fig. 33.]

[Fig. 34.]

secat BC aequaliter [Fig. 33]. Si enim tunc sit ponderum in C et B ea ratio quae BF ad FC, manebunt suis locis. Ergo diminuto pondere ex C donec aequale sit pendenti ex B, non amplius manebunt.

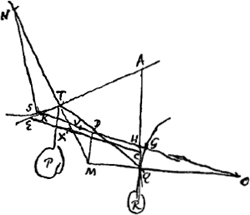
Ex fune NTQO fixo in N, O [Fig. 34] pendeant pondera P, R ligata in T et Q, ita ut si a puncto M, quo conveniunt productae NT, OQ, ducatur plano horizontis ad angulos rectos MD, ea secet TQ ut sint reciproce TD ad DQ sicut gravitas R ad P. dico pondera ita suspensa eo positu permanere.

Si enim non manent transferatur funis NT in NS et OQ in OG, adeoque TQ in SG, et dividatur SG in V similiter ac TQ in D. sitque S altius vel aeque altum ac G. Sit ATE funi NT ad angulos rectos, itemque AQ funi OQ. Itaque AE, AQ secabunt SG, quia S et G sunt in circumferentijs circulorum tangentium rectas AE, AQ in T et Q. sint autem dictarum intersectionum puncta K et H.

Manifestum vero rectas AE, AQ deorsum esse inclinatas, angulosque ATQ, AQT singulos minores recto, quia recti ATN, AQO; minores vero duobus rectis singuli NTQ, OQT, propter flexum funis NTQO in T et Q.

Quod si jam intra angulum EAQ aptetur EC parallela et aequalis SG, ea major erit quam KH; ideoque punctum E inferius quam K, ac proinde inferius quoque quam S quia recta GS versus S ascendere posita fuit, vel horizonti esse parallela. Itaque punctum X quo EC divisa ponatur similiter ac SG in V humilius erit puncto V. Atqui punctum X altius est puncto D, per praecedentem. Ergo multo magis punctum V altius erit quam D. Atque ita centrum gravitatis ponderum P, R ascendisset, quod impossibile.

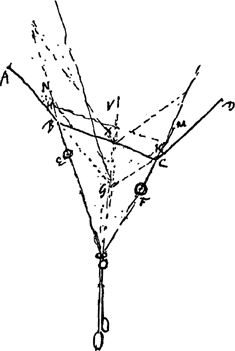
VII, B. § 4. Quand la pesanteur agit vers un point O [Fig. 35] ...³⁾.

3) Les poids E et F de la Fig. 35 sont fictifs et ne servent qu'à indiquer la tension des cordes impondérables. Dans la suite Huygens désigne, paraît-il, par EO et OF ou FO les longueurs des cordes BO et CO (dont les prolongements passent par l'anneau O et portent des poids à leurs extrémités). Il est vrai qu'en considérant BE et CF comme des longueurs constantes, d'ailleurs arbitraires, on peut également parler dans les propositions du texte des longueurs EO et FO (au lieu de BO et CO), mais ce serait là une bizarrerie inutile. L'anneau O occupe évidemment une position invariable, comme les points A et D; le centre de gravité des poids (E et F) suspendus aux deux cordes au-dessous de O tend à descendre autant que possible.

[p. 62]

[Fig. 35.]

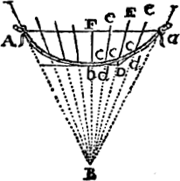
Pour determiner comment demeurera située la corde ABCD, avec des poids egaux E, F attachez en B, C, il faut trouver telle situation, que la somme de EO et OF soit la moindre possible. Et si les poids E, F sont inegaux, il faut que EO multipliee par le poids E, et FO multipliee par le poids F, facent ensemble la moindre somme.

Car par exemple si le poids F estoit double de E, il faudroit s'imaginer qu'il y a deux poids comme E pendus en F. Et alors il est certain que la somme de EO et de deux fois FO devroit estre la moindre possible, afin que le composè de tout le poids fust aussi proche de O¹⁾ qu'il le pourroit.

Or il faudroit, suivant le P. Pardies, que les 2 poids egaux [NB et MC] demeurassent lors que AB, DC prolongees se rencontrent dans la droite OG qui divise l'angle BOC en deux parties egales²⁾. Car alors il veut que le centre de gravitè des poids E, F, ou des lignes egalement pesantes NB, MC, se rencontre dans la droite OGV; ce qui n'est point; car s'il s'y rencontroit, comme en X, alors HX seroit a XK comme HO à KO, qui estant tousjours inegales, sinon alors que BO, OC sont egales, les poids H et K ne seroient point egaux, contre l'hypothese³⁾.

Je puis demontrer que OG prolongee doit passer par le centre de gravitè des poids placez en B, C⁴⁾.

1) Ou plutôt ‘aussi loin de O’, lorsque les poids se trouvent au-dessous de O. L'alinéa suivant fait voir pourquoi Huygens, dans la Fig. 35, a placé les poids au-dessus de O; le cas qu'il considère lui a été suggéré par un autre problème envisagé par Pardies (notes suivantes).

2) Ce qui serait exact (comparez la note 4 qui suit) dans le cas de forces tirantes égales E et F.

3) Pardies dans les Chap. 79 et 80 de son traité de 1673 ‘La Statique ou la Science des forces mouvantes’ ne considère pas le cas dont il est question dans les alinéas précédents (poids suspendus à des cordes passant par l'anneau O). Il écrit: ‘Si l'on suppose [Fig. 36] que les lignes de direction Fb, EC, ce ne sont pas parallèles, mais qu'elles concourent en bas au point B, la corde se rallongeant, se courberoit en Hyperbole ..... La raison en est, que divisant en deux également l'angle aBA par la ligne BF, l'angle aBE [lisez aBF] par la ligne BE, & l'angle aBE par la ligne Be; &c. & supposant que les portions des lignes ec, Ec, ec, Fb, &c. étant également pesantes, sont appuyées sur un filet indivisible; il est manifeste que le centre de gravité de toutes les lignes qui sont entre a & A se trouvera au milieu, sçavoir en la ligne Fh prolongée, s'il en est besoin; & le centre de celles qui sont entre a et F se trouvera aussi en la ligne de leurs milieux, sçavoir en BC, &c.’
Il n'est pas clair comment les barres pesantes telles que Ec sont maintenues en place, ni pourquoi ces barres exerceraient des forces dans le sens de leurs longueurs comme Pardies semble le supposer.
A la p. 9 du Manuscrit G Huygens écrit à propos des figures de Pardies des chapitres nommés:
Ces 5 lignes [Fig. 37] font avec leur prochaines des angles tous egaux au point B. Et leur parties CC sont egales.
Le P. Pardies pag. 138 des forces mouvantes conclud d'icy que le centre de gravitè de ces lignes se trouve dans celle du milieu BA. ce qui n'est point vray generalement.
Si les verges egales bb [Fig. 38] pressent la corde AB en s'eloignant du point C, le P. Pardies dit qu'elle se courbera en cercle ou en ellipse dont le foier opposè sera C. J'avoüe que si la longueur de la corde AbB est egale a la periferie du polygone inscrit dans un arc de cercle decrit du centre C par les points A B, alors cette corde se courbera circulairement, c'est a dire suivant le dit polygone. Mais quant a la figure Elliptique sa demonstration ne le prouve pas; et il y a bien autre chose a considerer. Car que diroit il si la corde gardant la dite longueur les verges bb la pressoient comme en s'ecartant d'un point plus proche D, qui alors ne peut pas estre le foier de l'Ellipse.

4) Dans le cas des forces tirantes E et F les moments des tensions E et F des cordes BO et CO autour du point G, intersection de AB et DC prolongées, doivent être égaux, puisqu'ils sont égaux l'un et l'autre au moment de la tension de la corde BC par rapport au même point. On peut en conclure que les composantes des forces E et F perpendiculaires, respectivement en B et en C, à BC ont même moment par rapport au point où OG prolongée coupe BC. Ce point d'intersection est donc le centre de gravité de poids E_p et F_p placés en B et C, où E_p et F_p désignent la grandeur des composantes perpendiculaires nommées. - On arrive au même résultat en considérant des déplacements virtuels des points B et C analogues à ceux de la Fig. 34 - G étant le centre instantané de rotation de la corde BC -, et en écrivant que la somme des travaux virtuels des tensions E et F est nulle.
Nous ignorons si c'est bien des poids E_p et F_p que Huygens a voulu parler.

[p. 63]

[Fig. 36.]

[Fig. 37.]

[Fig. 38.]

[p. 64]

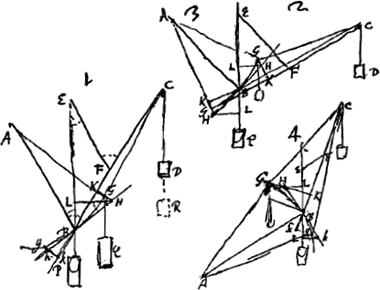[Fig. 39].

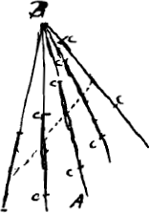
VII, B. § 5. Sustineatur pondus P [Fig. 39] funibus in diversa trahentibus⁵⁾ AB, BC. Ductaque BE ad horizontem perpendiculari agatur ex quolibet in ea puncto E, recta EF parallela AB, ac funi CB occurrens in F. Dico sicut EB ad BF ita esse pondus P ad momentum quo trahitur funis CB; hoc est si funis BC ducatur super trochlea in C posita, partique quae deinceps est appendatur pondus D, quod se habeat ad P. sicut FB ad BE, dico fieri hoc modo aequilibrium.

Si enim fieri potest, praeponderet D ac descendendo ad R attrahat punctum B in G,

5) Leçon alternative: divergentibus.

[p. 65]

ut funis jam sit AGCR⁶⁾. Et ducatur BH perpendicularis in AB, et occurrat ei recta KGH quae per punctum G perpendicularis ducitur in BC. Sitque HL perpendicularis in EB. Est igitur angulus BHL aequalis ABE, quia uterque seorsim cum angulo LBH rectum efficit. Similiterque angulus BHK aequalis ABK quia uterque cum angulo KBH rectum efficit. Sed BL est ad BK ut sinus anguli BHL ad sinum anguli BHK. Ergo BL ad BK ut sinus anguli ABE, seu BEF, ad sinum anguli ABK, seu EFC vel EFB. hoc est ut FB ad EB, quia trianguli cujusque latera eandem inter se rationem habent quam sinus angulorum quibus ea subtenduntur. Est autem ascensus perpendicularis puncti B per arcum BG major quam BL; quia semper punctum G altius quam H hoc est quam L. Sed pondus D minus descendit quam longitudine BK; quia tantum descendit quanto CB longior est quam CG, qui excessus minor est quam quo BC superat CK, hoc est quam KB, quia scilicet CG major quam CK. Itaque ascensus puncti B seu ponderis P ad descensum ponderis D majorem rationem habet quam BL ad BK ideoque majorem quam FB ad EB, hoc est quam pondus D ad P. Unde centrum gravitatis commune utriusque ponderis altius ascendisset. quod fieri non potest.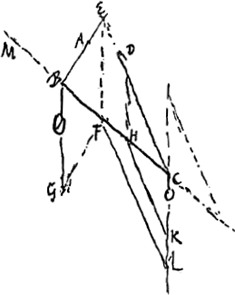

[Fig. 40.]

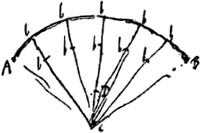
VII, B. § 6. BC [Fig. 40] linea inflexilis suspensa funibus AB, DC. Si quis sectâ virgâ BC in F, prehendat extremum F, et sustineat virga FB pressionem puncti B; eadem vi opus habebit ac si virgâ FC sustineat pressionem puncti C. quia alioqui junctis rursus extremis utriusque virgae in F, pars magis pressa minus pressam pelleret. ponitur autem virga BC manere.

Tanta est pressio virgae FB ad sustinendam BA, quanta tractio per funem MB ad hoc idem requiritur, hoc tamen demonstrari debet, non sumi tanquam per se manifestum⁷⁾.

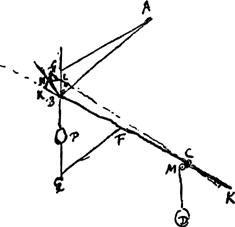
AB funis [Fig. 41]. BC virga inflexilis. C annulus fixus per quem extenditur virga BC usque in K, unde funis KCMD super trochleam M ducitur. Pondus aequare debet pressionem quae sentiretur in K.

6) En marge: Si praeponderans dicatur P et punctum B descendere in G, jam minus descendet P quam per BL et D amplius ascendet quam per BK &c. ut in 3^a figura [Fig. 39 No. 3].

7) Dans l'un et l'autre cas, il s'agit de l'équilibre de trois forces appliquées au point B. Il nous semble donc assez évident que la tension de la corde BM dans le deuxième cas est égale à la pression exercée par la verge CB dans le premier. Dans le cas de la Fig. 35 Huygens avait d'ailleurs admis lui-même comme évident cette équivalence d'une tension avec une pression.

[p. 66]

[Fig. 41.]

[Fig. 42.]

P in G magis ascendit quam per BL. D minus descendit quam quanta est longitudo BK. Sed BL ad BK [il y a deux lettres K dans la figure] ut BF ad BE, hoc est ut D ad P¹⁾.

VII, B. § 7²⁾. Hanc de curva Catenae disquisitionem ulterius prosecuti sumus pag. 82³⁾ et sequentibus. Definiendum quid petatur cum proponitur invenienda

1) Lorsque les déplacements sont infiniment petits, on peut dire que BL représente l'ascension du poids P et BK la descente du poids D. Comme il appert qu'on a identiquement P.BL = D.BK, l'équilibre est possible, ce qui n'a rien d'étonnant, pour des poids P et D quelconques.

2) Le § 7 est emprunté à la p. 58 du Manuscrit G, datant de septembre 1690: les p. 57 et 59 portent respectivement les dates du 7 et du 25 septembre. Nous en avons déjà publié le début dans la note 5 de la p. 504 du T. IX et la plus grande partie dans le § II de la p. 503 du même Tome. Voir aussi sur le contenu des p. 58 et suiv. du Manuscrit les p. 500-501 du T. IX et les §§ III et suiv. des p. 505 et suiv. du meme Tome.
Le problème de la chaînette avait été mis à l'ordre du jour en mai 1690 par Jacques Bernoulli; comparez la note 7 de la p. 497 du T. IX. Dans sa lettre du 9 octobre 1690 à Leibniz Huygens rappelle (T. IX, p. 498) qu'il s'était occupé de ce problème déjà à l'âge de 15 ans.

3) La p. 82 du Manuscrit (numération de Huygens) est celle que nous désignons par p. 93.

[p. 67]

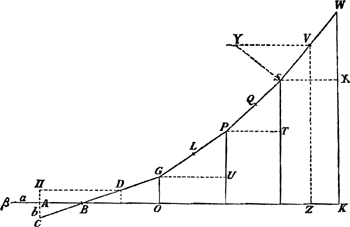
Curva secundum quam catena flectitur. An ut positis x et y normalibus ita ut x à puncto in data recta accipiatur, aequatione aliqua referatur x ad y. An ut posita quadratura circuli vel hyperbolae possent curvae quaesitae puncta quotlibet reperiri. An ut posita dimensione spatij alicujus denique, puncta ista inveniri queant. An sufficit proprietates aliquas ejus curvae invenire.

Catena [Fig. 42] composita ex virgulis aequalibus WS, SP, PG, GB et dimidia BA, quae est horizonti parallela. Catenae internodium βB horizonti parallelum ponitur, cujus dimidium AB. Eidem internodio singula BG, GP, PS, SW &c. aequalia. In singulis nodis pondera aequalia adnexa intelliguntur.

	CA		AB
GO ad OB ut	b	ad	a	} hoc facile absque calculo potest demonstrari, vid. p. 92^4).
PV ad VG ut	2b	ad	a	} hoc facile absque calculo potest demonstrari, vid. p. 92^4).
ST ad TP ut	3b	ad	a	} hoc facile absque calculo potest demonstrari, vid. p. 92^4).
WX ad XS ut	4b	ad	a	} hoc facile absque calculo potest demonstrari, vid. p. 92^4).

Angulorum GBO, PGV, SPT, WSX &c. tangentes aequaliter crescunt. Atqui BG, GP, PS, SW sunt aequales. Ergo GO, PV, ST, WX sunt sinus angulorum quorum tangentes aequaliter crescunt, et BO, GV, PT, SX eorundem angulorum sunt sinus complementorum.

VII, B. § 8⁵⁾. Melius sic. Catenae seu fili suspensi aequalia pondera innexa habentis, si infimum internodium horizonti parallelum fuerit, erunt deinceps anguli reliquorum internodiorum cum plano horizontali tales, ut eorum tangentes crescant secundum rationem numerorum ab unitate incipientium 1, 2, 3, 4, 5 &c.

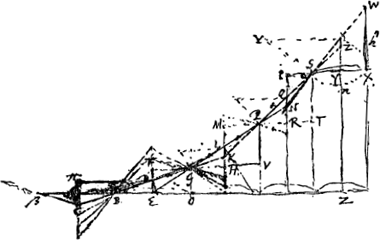
Fundamentum omnium eorum quae de Curva Catenae [Fig. 43] reperimus⁶⁾. Fili gravitate carentis, et aequalia pondera innexa habentis, tria quaelibet internodia continua ac sursum tendentia, ita ad planum horizontale inclinantur, ut tangentes angulorum hujus inclinationis crescant aequali excessu.

Sint catenae pondera aequalia innexa habentis A, B, C, D internodia tria sursum tendentia AB, BC, CD, etc.... Ergo constat propositum.

4) Notre p. 97. Voir le § 8 qui suit.

4) Notre p. 97. Voir le § 8 qui suit.

4) Notre p. 97. Voir le § 8 qui suit.

4) Notre p. 97. Voir le § 8 qui suit.

5) Manuscrit G, p. 97; comparez les notes 3 et 4. La p. 92 porte la date du 28 mars et la p. 104 celle du 22 avril 1691. L'alinéa: ‘Catenae seu fili..... 1, 2, 3, 4, 5 &c.’ a déjà été publié à la p. 503 du T. IX.

6) La partie ‘Fundamentum omnium .... Ergo constat propositum’ de ce § a déjà été publié au § I de la p. 502 du T. IX.

[p. 68]

[Fig. 43.]

Hinc si infimum internodiorum quotlibet fuerit horizonti parallelum, erunt tangentes angulorum inclinationis ad horizontem sequentium deinceps internodiorum in ratione numerorum ab unitate 1, 2, 3, 4, 5 &c. quia tunc facile ostenditur primi et secundi surgentium internodiorum angulos ad planum horizontalem habere tangentes ut 1 ad 2.