Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 48]

VI.¹⁾
Force nécessaire pour faire surmonter à la roue d'une charrette un obstacle donné.
[1668]

[Fig. 21.]⁴⁾

VI, § I. Des poids²⁾ egaux estant chargez sur des charrettes³⁾ dont les roues de l'une soient plus hautes que celles de l'autre, il faut pour vaincre la resistence qu'apportent les chemins raboteux, que la force qui tire les petites roues a celle qui tire les grandes, soit en raison sousdoublee ou mesme un peu plus de celle qu'a le diametre des grandes roues au diametre des petites. Par exemple si les grandes roues sont deux sois si hautes que les petites, 5 chevaux n'auront pas tant de peine à tirer un canon chargè sur les grandes [Fig. 21] que 7 chevaux a tirer le mesme canon chargè sur les petites.

Soit AB la grande roue, DE la petite [Fig. 22], qui roulant toutes deux sur un plan horizontal qu'elles touchent en B et E, rencontrent des hauteurs egales a surmonter HG et KL, par exemple des pierres qui soient dans le chemin horizontal BE, et posons que leurs fardeaux egaux appuient sur les centres C, F. La roue AB touchant sa pierre au point

1) Manuscrit C, p. 259. Les p. 251 et 261 portent respectivement les dates de mai 1668 et du 14 juillet 1668. Voir sur cette Pièce la p. 19 qui précède.

4) Les connaisseurs de l'histoire de l'artillerie nous assurent qu'il s'agit ici d'un dessin fantaisiste; on ne connaît pas de canon placé au-dessous de l'axe de l'affut.

2) Leçon alternative: fardeaux.

3) D'après la p.107 (Livre I, Ch. II) du T. I de l'‘Etude sur le passé et l'avenir de l'Artillerie’ par le prince Napoléon Louis Bonaparte (Paris, J. Dumaine, 1846) on se servait en ce temps de l'‘expression de charrettes pour désigner les gros calibres’.

[p. 49]

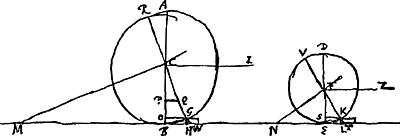[Fig. 22.]

G, soit menè par le centre C le diametre RCG qui estant produit rencontre BE en W, et CM perpendiculaire a ce diametre, rencontrant le plan BE en M. et soit fait de mesme a legard de la roue DE, qui rencontrant la pierre en K, le diametre menè à ce point soit VFK rencontrant BE en T, et soit FN perpendiculaire sur ce diametre. Il est certain qu'après que la roue AB aura rencontrè la pierre en G, son centre commencera a se mouvoir dans une circonference de cercle decrite du centre G, et dont la tangente au point C est CM, de sorte qu'il faut la mesme force pour la tirer en avant comme si on vouloit faire monter le fardeau le long du plan inclinè MC, en tirant par la corde horizontale CI. D'ou s'en suit par la precedente⁵⁾ que la force qui tire par cette corde doit estre au poids absolu du fardeau, comme la ligne CB à BM, c'est a dire comme WB à BC. De mesme pour tirer la roue DE apres qu'elle a touchè a la pierre en K il faut que la force qui agit par la corde horizontale FZ soit au poids absolu du fardeau comme la ligne FE ad EN, ou comme TE à EF.

Du rayon CB soit couppèe CP egale au rayon FE, et menee PQ parallele à BH. Donc puisque la force qui tire la roue AB est au poids absolu du fardeau comme WB à BC, c'est a dire comme QP a PC, et que la force qui tire la roue DE est au mesme poids absolu du fardeau comme TE a EF egale a PC, il s'ensuit que cette derniere force est a la premiere comme TE a PQ. Or parce que KL, GH sont egales et l'angle LKT plus grand que HGW, il s'en suit que KT est plus grande que GW. Partant le ▭ VKT aura plus grande raison au ▭ WGR que KV à GR. Et adjoutant au ▭ VKT le quarrè TK, et au ▭ WGR le quarrè WG, les 2 premiers c'est a dire le ▭ VTK, aura plus grande raison au deux derniers, qui font le ▭ RWG, que KV à GR. Mais le ▭ VTK est egal au quarrè TE, et le ▭ RWG egal au quarrè WB; donc le quarrè TE aura plus grande raison au quarrè WB que le diametre VK au diametre RG. c'est a dire que FE ou PC a CB, ou bien que PQ a BW. Et partant TE est plus grande que moiene proportionnelle entre PQ et BW. d'ou s'en suit que

5) C.à.d. par la p. 258 du Manuscrit C, mentionnée aussi dans la note 1 de la p. 34 qui précède.

[p. 50]

la raison de TE à PQ, qui est la mesme que celle de la force qui tire la roue DE a celle qui tire la roue AB, est plus grande que sous double de la raison de BW a PQ, c'est a dire de BC a PC, ou bien de celle du diametre AB au diametre DE. ce qu'il falloit demonstrer.

Le § 2 est tiré du T. III des Registres de l'Académie des Sciences.

VI, § 2. Du Mercredy 11^e Juillet 1668.

Le Mercredy 11^e jour de Juillet 1668 la Compagnie estant assemblée au lieu ordinaire on a continué de traicter, quelle est l'aduantage des grandes roües sur les petites pour la facilité du charoy.

Sur cela M^r Hugens a dict, que des fardeaux egaux estant menez sur des roües de differente grandeur, il faut pour vaincre la resistence qu'apportent les chemins rabotteux que la force ... etc., comme au § 1. Les variantes sont absolument insignifiantes.

Après Huygens Mariotte parla sur le même sujet. Roberval en avait déjà parlé le 4 juillet (et après lui Buot). Il suppose, comme Huygens, que la roue ‘rencontre dans le chemin quelque pierre dont la hauteur prise a plomb soit [donnée]’.

Voyez aussi les p. 40-41 de l'‘Historia’ de du Hamel.