Oeuvres complètes. Tome XIX. Mécanique théorique et physique 1666-1695

[p. 35]

IV.
Equilibre de deux verges¹⁾.
(Cas d'équilibre stable).
[1673 ou 1674]

[Fig. 8.]

A et B [Fig. 8] sont deux poulies egales tirees par des poids egaux O et N. a l'une est attachee fixement la verge ACG, a l'autre la verge BC, qui est pressée par dessus par ACG, et luy resiste par sa pression vers en haut. Or a fin que ces deux pressions s'egalent l'une l'autre, il faut qu'en supposant un commencement de mouvement, par le quel, par exemple, le point C de la verge AG descende en H, et l'extremitè de la verge BC en E, il faut dis je que les angles CAH, CBE soient egaux entre eux, afin que le poids O foit descendu autant que le poids N sera montè.

Soient AC, AH prolongees jusqu'a ce que AG, AL soient chacune egales à BC.

1) La Pièce IV est empruntée à une feuille séparée (Chartae mechanicae, f. 128). Huygens traite la même question en latin à la p. 434 du Manuscrit D datant de 1673 ou 1674 (les p. 391 du Manuscrit D et 26 du Manuscrit E portent respectivement des dates de juillet 1673 et de décembre 1674); nous ne reproduisons pas la pièce latine.

[p. 36]

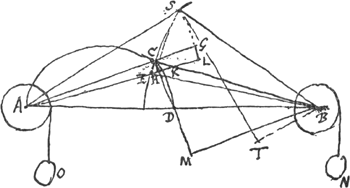
Joignant donc GL, elle doit estre egale a CE soutendente de l'arc CE; la quelle est censee perpendiculaire aux deux rayons BC, BE, a cause que l'angle CBE est infiniment petit. Et de mesme la soutendente de l'arc CH est censee perpendiculaire sur AH et AC. Puisque donc GL est egale a CE la raison de GL à CH sera la mesme que CE ad CH, ou CK à KH, ou CB à BM, ayant menè BM perpendiculaire sur CHM. Mais comme GL à CH ainsi GA à AC, ou bien BC à AC. Donc BC sera à AC comme BC à BM. Et par consequent BM egale à AC. Et BD egale à DA, puisque les angles DBM, DAC sont egaux et les angles BMD, ACD droits. Le point D est donc donnè, et le point C est dans la circonference d'un demicercle sur AD. Mais il est aussi a la circonference descrite du rayon BC qui est donnè. Donc le point C est dans l'intersection de ces deux circonferences, et partant il est donnè.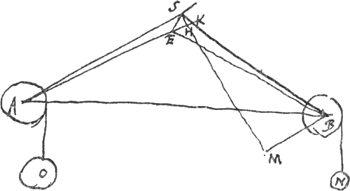

[Fig. 9.]

Par le mesme principe l'on trouve que lors que les verges AS, BS [Fig. 9] sont d'égale longueur, mais posees en sorte que AS presse par dessus le bout de la verge BS, pour faire equilibre, il faut que le poids O soit à N comme la longueur AS ou BS à BM, supposant BM parallele a AS et SM pdrpendiculaire à BM.

Car cela estant, si on suppose un commencement de mouvement, en sorte que le point S de la verge AS descende en H, et le bout de la verge BS en E, l'angle SBE sera a l'angle SAH, comme SE à SH, ou comme KE à KS, ou comme SB à BM, car les triangles EKS, SBM sont semblables, parce qu'ils sont rectangles, et que l'angle EKS est censè egal a MBS. Or comme l'angle SBE à SAH, ainsi est la montée du poids N a la descente du poids O. Donc elles sont en proportion reciproque des poids mesmes. Et partant le centre commun de leur gravitè demeure a mesme hauteur ou il estoit devant le mouvement.