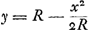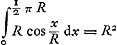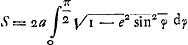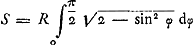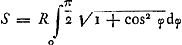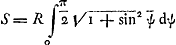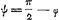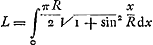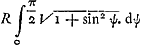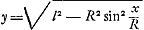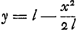|
| |
| |
| |
II.
L'application de décembre 1683 des vibrations de torsion aux horloges marines (pendulum cylindricum trichordon)Ga naar voetnoot1).
[Fig. 22.]

[Fig. 23.]
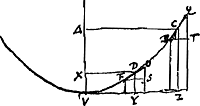
[Fig. 24.]
| |
§ 1.
ἑυρηϰα Hagae, 4 Dec. 1683.
Pendulum cylindricum Trichordon [Fig. 22]. Inventum postquam elaterem spiralem frigore accelerare motum horologij repperiGa naar voetnoot2). Hic effectum elateris absque elatere habemusGa naar voetnoot3). Aequalitas recursuum existeret si punctum moveretur in parabola cujus ½ lat. rectum AB [Fig. 23], cylindro circumplicata. AB ∞ diam. BN [Fig. 23]Ga naar voetnoot4). Demonstratio hinc. Si parabolam [Fig. 24] tangant rectae FO, BQ in punctis D et C, unde ducantur perpendiculares in VZ, tangentem in vertice, rectae autem ab FO et à BQ eidem VZ perpendiculares intercipiant partes ejus aequales, sintque FS, BT ipsi VZ parallelaeGa naar voetnoot5) erit QT ad OS ut C∆ ad DX, sive ut ZV ad YV. Sed VY, VZ sunt
| |
| |
distantiae quibus a quiete extrahitur punctum B in figura cylindri [Fig. 23], quantum ad motum horizontalem. Renitentiae vero itemque incitationes ponderis B horizontaliter tracti in punctis parabolae D, C [Fig. 24], sunt inter se ut QT ad OS quia BT, FS aequalesGa naar voetnoot1). Igitur erunt etiam istae incitationes ut ZV ad YV. Unde aequalitas recursuumGa naar voetnoot2).
AB ∞ diam. BN [Fig. 23]. Si BK sit ⅛ circumferentiae, fient recursus ¼ ipsius. fit punctum G inferius P, ubi esse deberet ad aequabilis motus lineam describendam, tantum 1/1000 AB, posita nempe BPLR parabolaGa naar voetnoot3) ut oportet.
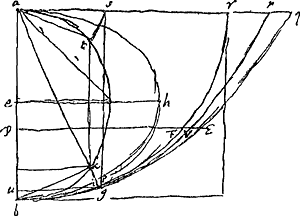
[Fig. 25.]
| |
§ 2.
7 Dec. 1683.
Circulo AQ [Fig. 23] immoto, movetur horizontaliter circulus hic BN tribus filis è superiore suspensus, unde circulus hic sursum sertur. Et punctum B describit curvam quandam BGOQ in superficie cylindrica, quae curva si cum superficie illa in planum explicetur erit linea sinuum quam vocant, in qua si ad axem ba [Fig. 25] applicetur quopiam DE normaliter, ea aequabitur arcui bF à quadrante br abscisso.
Imo parabola bvr cujus semilatus rectum ab.
| |
| |
Si enim quaeratur hujus curvae punctum G [Fig. 23] in recta KS, constat junctâ SA angulum ASG esse rectum. unde quadr. SG aequale differentiae quadratorum AG, AS quorum AG qu. aequale est AB sive AQ. unde qu. SG ∞ qu. SQ sive KN. Evoluto igitur arcu BK, sive in altera figura [Fig. 25] arcu at in as, si ponatur perpendicularis sg aequalis KN sive in altera, ak, habebitur in plano evoluto punctum g. Ducatur gu applicata, quae secet arcum bFr in i. Quod si jam ostendatur ug ∞ arcui bi, erit punctum g in curva illa sinuumGa naar voetnoot4). Ostenditur autem sic. Cum sg sive au sit ∞ ak ex constructione, erit perpendicularis iu aequalis bk, quia producta ak incidit in iGa naar voetnoot5). Unde arcus bi aequalis erit arcui bk quiaGa naar voetnoot6) &c. sed bk arcus aequalis est rectae as sive ug. Ergo ug aequalis arcui bi. quod erat demonstrandumGa naar voetnoot7).
| |
| |
Spatium bgεqab est aequale quadrato ab abGa naar voetnoot1).
Curva bgεq est aequalis curvae dimidiae Ellipsis ahb posita eh potentiâ dupla ad radium aeGa naar voetnoot2).
| |
§ 3.
Quaecunque fuerit longitudo filorum AB [Fig. 23 et 26] semper motus iso-
| |
| |
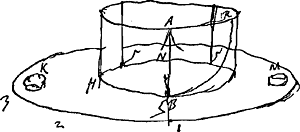
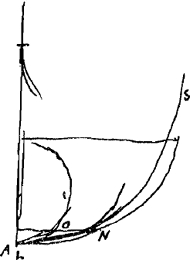
chronus est per parabolam BR cylindro applicatam cujus ½ latus rectum AB Ga naar voetnoot3).
Pondere orbis BHN aut annuli aucto, idem tempus recursus permanetGa naar voetnoot4). Sed extenso orbe vel circumferentia pensili pondus continente lentior evadit motus secundum rationem diametrorumGa naar voetnoot5). Ponamus duplam.
| |
| |
Fit itaque motus ponderum per similes arcus duplo major, posita eadem altitudine ascensus. unde tempora sunt in cycloidibus, ubi, in eadem altitudine, arcus sunt dupli [Fig. 27]. quod ut fiat debent subtensae LO, LN in circumferentijs circulorum genitorum esse in ratione dupla. unde diametri in quadrupla. diametri autem bis sumptae faciunt pendula istarum cycloidum; quorum igitur longitudo rationis quadruplae, facit recursuum tempora rationis duplae.
Ponderibus minoribus K, M, ponderi orbis additis [Fig. 26]Ga naar voetnoot1), poterimus ea versus centrum promovendo, accelerare non nihil recursuum tempora; sed sciendum longe minus in hoc ipsorum esse momentum quam in circulis simpliciter suspensis e centroGa naar voetnoot2).
Quadruplicando fila AB, fit motus duplo lentior, ut in pendulisGa naar voetnoot3). Si duplicetur distantia filorum AB à centro, manente eodem annulo, erunt tempora ut in cycloidibus, ubi, in aequalibus arcubus, altitudines sunt quadruplae. unde efficitur tempora hic fore subdupla priorumGa naar voetnoot4).

[Fig. 28.]
| |
§ 4.
Le 17 dec. 1683 j'ay portè a Van Ceulen l'horloger le modelle que j'avois fait de ce mouvement de Pendule Cylindrique, pour changer de cette facon les 2 horloges que je luy avois fait faire pour la Compagnie des Indes OrientalesGa naar voetnoot5). J'avois priè mon frere de Zeelhem de venir avec moy: parce que ledit horloger s'imaginoit d'avoir trouvè la mesme chose que moyGa naar voetnoot6), apres m'en avoir ouy dire quelque chose en gros. Mais ayant vu le modelle il avoua que ce qu'il avoit modelè n'y ressembloit nullement.
| |
§ 5.
10 Jun. 1684.
Optima ratio horum si filis longis utamur [Fig. 28] puta 9½ vel 38 pollicum quae extremo annuli margini illigentur, atque ita circulare pendulum fiat; axe annuli in foramen stabile immisso propter navis motum.
| |
| |
| |
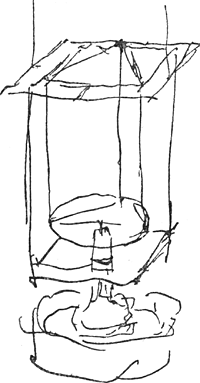
[Fig. 29.]
que l'on ne doit pas demander ces mouvements [Fig. 29] dans une derniere egalitè, mais a peu pres.
que l'invention de la detente sans manquer est de grande importanceGa naar voetnoot8) qui peut etre appliquée au pendule triangulaireGa naar voetnoot9).
que ces messieurs les directeurs de la Compagnie des Indes ne devroient pas regarder a quelque peu de depense, pour arriver a cette invention si utileGa naar voetnoot10).
Tourner les horloges faits pour en faire des pendules triangulairesGa naar voetnoot11). l'une au moins. et laisser l'autre comme elle est pour la grande agitation du vaisseau.
| |
Resolutiën van de Bewinthebberen van de Oostindische Comp.ie ter Camer tot Amsterdam.
Donderdag den 27sten Julij 1684.... Den Heer Burgemeester Hudde heeft ter vergaderingh geproponeert, dat sijn Ed.t bij resolutien van den 31sten December 1682
| |
| |
en 28 Februarij 1684 geauthoriseert sijnde, om met den Heer Huijgens en eenen van Ceulen te corresponderen over het uijtvinden en maeken van seer accurate horologien, die van malkanderen in een etmael geen secunde souden verlopen, waerdoor soude cunnen werden uijtgevonden het Oost en West en daer aen te spenderen een à twee duijsent gulden, sijn Ed.t dat werck soo veel in hem is geweest heeft voortgeset, sonder dat evenwel tot noch toe het gewenschte ooghwit is bereijckt; dat sijn Ed.t best geacht heeft, alvoren verder te continueren, hier van kennisse aen dese vergaderingh te geven, item voor te stellen, of de selve soude cunnen goetvinden te doen uijttellen aen den voornoemden van Ceulen, een man van weijnigh vermogenGa naar voetnoot1), twee honderd silvere ducatons, op reeckeningh van sijnen gedanen arbeijt; waarop sijnde gedelibereert, is verstaen den Heer Burgemeester Hudde voor sijne gedane communicatie te bedancken, sijn Ed.t te versoecken, om conform de resolutien hier boven geallegueert, den Heer Huygens te versoecken en te animeren, om in sijnen goeden ijver te willen continueren; wijders aen den voornoemden van Ceulen toe te laten komen de voorsz. twee hondert ducatons, om ware het doenlijk dese dienstige saeke tot perfectie te brengen.
Donderdagh den 30 August: 1685 ... Den Heer Burgemeester Hudde de vergaderingh voorgedragen hebbende, dat den Heer Huijgens presenteertGa naar voetnoot2) personelijk een preuve in zee te nemen van de accurate horologien bij sijn Ed.t uijtgevonden, en met voorkennisse van dese vergaderingh gedaen maeken, of deselve de bewegingen vande zee kunnen uijtstaen, waer door als dan gemeijnt werd, dat soude cunnen werden uijtgevonden het Oost en West, soo als daer toe de resolutien van den 31 December 1682, 28 Februarij, en 27 Julij 1684 tenderen, is de voorsz. propositie en presentatie voor gansch aengenaem opgenomen, en is dienvolgende verstaen dat den voornoemden Heer Huijgens daer toe sal werden gepresenteert het galjot van Comp.ie alhier, en den persoon van Barent FockesGa naar voetnoot3), om het selve te voeren, die sigh sal posteren en seijlen daer het sijn Ed.t goetvinden sal; werdende de Heeren van de Equippagie versocht en geauthoriseert, om het daer toe bequaem te maeken. En den gemelten Heer Burgemeester Hudde om den horologie maecker van Ceulen, die het werck heeft gemaeckt, te laten toekomen voor de tweede mael twee hondert ducatons, mitsgaders aen de Smith, die daer toe heeft geholpen seventigh gulden, met
| |
| |
verder versoeck op den welgemelten Heer Hudde om hier over het opsicht en directie te blijven houden, ten eijnde dat dessein tot verlightinge van de zeevaert ten goeden effecte magh werden gebraght.
Donderdagh den 6 September 1685 .... De Heer Burgemeester Hudde ter vergaderingh gecommuniceert hebbende seeckere missive door den Heer Huygens aen Sijn Ed.t geschrevenGa naar voetnoot4), waer bij den selven Heer Huijgens versocht, dat dese vergaderingh hem in de aenstaende toght om preuve te nemen van de horologien bij sijn Ed.t uijtgevonden, waer door te vinden soude wesen het Oost en West breder in de resolutie van den 30 des voorleden maents en andere meer vervat, soude willen toevoegen Mr. de GraefGa naar voetnoot5) of iemant anders in die materie ervaren, tot sijn Ed.s assistentie en getuijge, is verstaen den welgemelten Heer Burgemeester te versoecken en te authoriseren, om den voorn. de Graef of een ander daer toe te disponeren, sijnde wijders sijn WelEd.t voor de gedaene openingh bedanckt.
|
-
voetnoot1)
- La Pièce, que nous divisons en cinq §§, est empruntée aux p. 179-180 du Manuscrit F.
-
voetnoot2)
- Voir sur la question de l'influence de la température sur la période de vibration des ressorts spiraux la p. 508 l'Avertissement qui précède.
-
voetnoot3)
- Il y a donc ici une certaine continuité: comparez la p. 509 de l'Avertissement.
-
voetnoot4)
- Voir sur la courbe décrite par le point B le § 2 qui suit, notamment les notes 4 et 7 de la p. 529.
-
voetnoot1)
- Dans l'état de repos la tension de chacun des trois fils est ⅓ G, G étant le poids du cercle insérieur. Lorsqu'on tourne ce cercle de manière que les trois fils font désormais un angle α avec la verticale, et qu'on maintient le cercle dans cette position en appliquant une force horizontale tangentielle K (‘renitentia’) en chacune des extrémités inférieures des fils, la tension S des fils, dont la composante verticale est toujours ⅓ G, sera telle que K = ⅓ G tg α. Les forces K égales et contraires qui mettent le cercle en mouvement lorsqu'on ne le retient plus (‘incitationes’) sont donc proportionnelles à tg α. Or α est aussi l'angle entre la tangente à la courbe que l'extrémité inférieure du fil va décrire et la projection de la tangente sur un plan horizontal (puisque la tangente est perpendiculaire au fil). Les ‘renitentiae’ en D et C [Fig. 24] seraient donc proportionnelles à QT/BT et OS/FS respectivement (c.à.d. à QT et OS, puisque BT = FS), si la courbe décrite, rendue plane par le développement du cylindre de la Fig. 23, était une parabole.
-
voetnoot2)
- D'après les p. 483 et suiv. du présent Tome.
-
voetnoot3)
- Après le développement du cylindre sur un plan.
-
voetnoot4)
- En prenant dans la Fig. 25 aq pour axe des x et ab pour axe des y, on peut en effet démontrer qu'une courbe construite de telle manière que l'abscisse ug ou x, sur laquelle se trouve le point i, est égale à l'arc bi du quart de circonférence bFr, a pour équation y = R cos x/R, en posant ab = R: la courbe est donc une sinusoïde. Voyez sur l'histoire de la sinusoïde la p. 511 de l'Avertissement qui précède.
Cette mise en équation ne correspond évidemment pas avec le raisonnement de Huygens. Il avait considéré en 1658 la courbe (BR VC de la Fig. 4 de la p. 348 du T. XIV) provenant du développement sur un plan de la surface courbe d'un onglet cylindrique: il avait constaté que l'ellipse qui limite cet onglet est changée de cette façon en une courbe - Roberval (voir à la p. 108 des ‘Divers Ouvrages de Math. et de Phys. par MM. de l'Ac. R. des Sciences’ de 1693, ses ‘Observations sur la composition des mouvements etc.’) l'appelle la ‘compagne de la cycloïde’ - pour laquelle (dans la figure nommée du T. XIV) HR = arc BK (l. 10 d'en bas de la p. 348), ce qui correspond dans la présente Fig. 25 à l'égalité de x ou ug avec l'arc bi. Dès que cette dernière égalité a été démontrée dans le cas de la Fig. 25, il apparaît que la ligne en question est la même que celle considérée en 1658 (à laquelle Huygens ne donnait pas encore en ce temps le nom de ‘linea sinuum’).
Ceci ne veut pas dire que dans la présente Fig. 23 la ligne tracée par le point B sur le cylindre soit une ellipse. En effet dans l'équation y = R cos x/R la longueur R est le diamètre du cylindre; tandis que dans le cas des Fig. 3 et 4 de la p. 348 du T. XIV on obtient la même équation y = r cos x/r(le plan qui coupe le cylindre étant incliné à 45o; si l'angle d'inclinaison était β, on trouverait y = r tg. β cos x/r) où r représente le rayon du cylindre. Dans la présente Fig. 25 la demi-circonférence bkta correspond à la demi-circonférence BKN de la Fig. 23; mais la circonférence à rayon R est bFr et c'est sur elle que se trouve le point i.
-
voetnoot5)
- Les triangles aui et akb sont congruents, puisqu'ils sont rectangles et qu'on a de plus ai = ab et au = ak. D'où résulte à la fois que le prolongement de ak passe par le point i et que iu = bk.
-
voetnoot6)
- L'égalité des arcs bi et bk résulte de l'égalité des angles bai
et bak, et du fait que le rayon du quart de circonférence biFr est le double de celui de la demi-circonférence bka.
-
voetnoot7)
- En comparant (Fig. 25) la courbe bgq ou y = R cos x/R (note 4) avec la parabole bvr à demi latus rectum ab ou R, dont il est aussi question dans la Fig. 24 et le § 1, et qui a pour équation
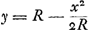 , on voit que la différence des ordonnées pour une même valeur de x (PG dans la Fig. 23) est R (cos x/R - 1) + x2/2R, ou 1/R3 [ x4/4! - x6/6!R2 + x8/8! R4 ... ], ce qui est inférieur à x4/4! R3, donc aussi à 1/1000 R, pour x = π/8 R, valeur considérée par Huygens dans le § 1. , on voit que la différence des ordonnées pour une même valeur de x (PG dans la Fig. 23) est R (cos x/R - 1) + x2/2R, ou 1/R3 [ x4/4! - x6/6!R2 + x8/8! R4 ... ], ce qui est inférieur à x4/4! R3, donc aussi à 1/1000 R, pour x = π/8 R, valeur considérée par Huygens dans le § 1.
Comment est-il arrivé à cette conclusion? Nous nous proposons de revenir sur cette question purement mathématique dans un des Tomes suivants.
-
voetnoot1)
- On a en effet
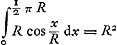 . Voir sur la démonstration de Huygens les deux premières lignes de la p. 349 du T. XIV et comparez, sur cette quadrature, le dernier alinéa de la p. 52 du T. I (lettre de Mersenne à Huygens de janvier 1647); Mersenne parle (sans le nommer) d'un résultat obtenu par Roberval; voir la p. 95 du supplément de 1922 par C. de Waard à l'édition des Oeuvres de Fermat par Tannery et Henry (Paris, Gauthier-Villars). . Voir sur la démonstration de Huygens les deux premières lignes de la p. 349 du T. XIV et comparez, sur cette quadrature, le dernier alinéa de la p. 52 du T. I (lettre de Mersenne à Huygens de janvier 1647); Mersenne parle (sans le nommer) d'un résultat obtenu par Roberval; voir la p. 95 du supplément de 1922 par C. de Waard à l'édition des Oeuvres de Fermat par Tannery et Henry (Paris, Gauthier-Villars).
-
voetnoot2)
- On peut vérifier de la manière suivante l'exactitude de ce résultat. La longueur de la moitié de l'ellipse qui a pour équation x2/a2 + y2/b2 = 1, où a > b, est
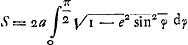 , où x/a = sin φ et e2 = a2 - b2/a2. Dans le cas considéré par Huygens a = ½ R √2 et b = ½ R. On a donc: , où x/a = sin φ et e2 = a2 - b2/a2. Dans le cas considéré par Huygens a = ½ R √2 et b = ½ R. On a donc: 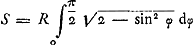 , ou bien , ou bien 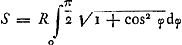 , ou encore , ou encore 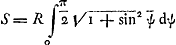 , en prenant , en prenant 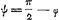 . Quant à la longueur de l'arc considéré de la sinusoïde y = R cos x/R, elle est . Quant à la longueur de l'arc considéré de la sinusoïde y = R cos x/R, elle est 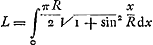 , ce qui se réduit également, en posant x/R = ψ, à la valeur , ce qui se réduit également, en posant x/R = ψ, à la valeur 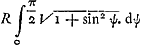 . On a donc L = S. C. Q. F. D. . On a donc L = S. C. Q. F. D.
Rappelons, sans tâcher pour le moment de reconstituer le raisonnement de Huygens - voir la fin de la note 7 de la p. 529 - que Pascal dans la lettre de 1659 de ‘A. Dettonville’ à Huygens (notre T. II, p. 307, 397) réduit ‘la dimension des lignes de toutes sortes de roulettes ... à des lignes eliptiques’.
-
voetnoot3)
- Cette affirmation n'est pas corroborée, comme précédemment (fin du § 1 et note 7 de la p. 529) - et comme Huygens aurait sans doute pu le faire ici aussi -, par une évaluation numérique de la différence des ordonnées, pour une même abscisse donnée, de la ligne décrite sur le cylindre par le point B, et de la parabole nommée, appliquée au cylindre. Lorsqu'on développe le cylindre sur un plan, la ligne décrite par B devient une courbe à équation
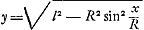 , l étant la longueur des fils, et R, comme précédemment, le diamètre du cylindre. Les axes sont choisis comme dans la note 7 nommée. L'équation de la parabole est , l étant la longueur des fils, et R, comme précédemment, le diamètre du cylindre. Les axes sont choisis comme dans la note 7 nommée. L'équation de la parabole est 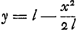 . Le développement en série fait voir que la différence des ordonnées des deux courbes (la première moins la deuxième) pour une même valeur de x a pour premier terme x4/2l[1/3R2 - 1/4l2]. Le terme en x2 disparaît donc comme dans le cas l = R considéré dans la note 7, de sorte que le mouvement est toujours approximativement isochrone, ainsi que Huygens le dit. . Le développement en série fait voir que la différence des ordonnées des deux courbes (la première moins la deuxième) pour une même valeur de x a pour premier terme x4/2l[1/3R2 - 1/4l2]. Le terme en x2 disparaît donc comme dans le cas l = R considéré dans la note 7, de sorte que le mouvement est toujours approximativement isochrone, ainsi que Huygens le dit.
-
voetnoot4)
- À cause, peut-on-dire, de la proportionnalité de la pesanteur et de la masse: comparez la note 7 de la p. 45 qui précède, et la note 3 de la p. 578 qui suit.
-
voetnoot5)
- Puisque le moment d'inertie I du cercle mobile augmente dans la proportion n4 lorsque le rayon devient n fois plus grand (l'épaisseur et le poids spécifique restant les mêmes), que le moment des forces agissant sur le cercle pour un angle de torsion donné devient en même temps, comme le poids, n2 fois plus grand, et que la période est proportionnelle à la racine carrée du quotient de I par le moment des forces pour un angle de torsion donné.
Huygens, dans la démonstration du texte qui suit, assimile les oscillations considérées autour de l'axe vertical à des vibrations linéaires, comme nous l'avons déjà dit à la p. 512 de l'Avertissement qui précède. Voir encore à ce sujet la note 4 de la p. 567 qui suit.
-
voetnoot1)
- Comparez la note 2 de la p. 28 du T. XVII.
-
voetnoot2)
- Dans les deux cas le moment d'inertie I varie par hypothèse de la même quantité. Mais le moment des forces est bien plus petit lorsque le cercle n'est suspendu qu'à un seul fil tordu. Le ∂T/∂I (où T est la période), qui est inversement proportionnel, comme T elle-même, à la racine carrée du moment des forces pour un écart angulaire donné, est d'autant plus grand que ce moment est plus petit.
-
voetnoot3)
- Caeteris paribus, le moment des forces est proportionnel à tg α (note 1 de la p. 528), c.à.d. à fort peu près à la longueur des fils. Et la période est inversement proportionnelle à la racine carrée du moment des forces.
-
voetnoot4)
- Le moment des forces étant doublé, la période sera diminuée dans le rapport √2.
-
voetnoot5)
- Comparez la p. 513 de l'Avertissement qui précède.
-
voetnoot6)
- Comparez la note 9 de la p. 32 qui précède.
-
voetnoot7)
- Le ‘§ 6’ est emprunté à la p. 192 du Manuscrit F. La p. 193 porte la date du 2 mai 1684. Toutefois il paraît probable que le § 6 date de fin 1685: comparez le 4ième alinéa avec le premier alinéa de la p. 539.
-
voetnoot8)
- Nous ne savons pas exactement de quelle invention il s'agit. Il semble bien que Huygens parle ici de la construction d'un remontoir (comparez l'expression ‘ontsluijtingh’, p.e. dans la note 2 de la p. 17 qui précède). Il est en effet presque certain que les horloges à ‘pendulum cylindricum trichordon’ construites par J. van Ceulen ont été des remontoirs à ressorts, remarque qui s'applique aussi aux horloges à ressort spiral qui furent changées en elles (l. 7 de la p. 510). Comparez la note 11.
-
voetnoot9)
- Nous savons en effet que l'horloge à pendule triangulaire qui fait son apparition en 1685, était un remontoir: voir p.e. la note citée dans la note précédente, et la Pièce IV qui suit (p. 539).
-
voetnoot10)
- Comparez les p. 509-511 de l'Avertissement qui précède.
-
voetnoot11)
- Cette remarque porte à croire (comparez la note 8) que l'agencement des roues des horloges à ‘pendulum cylindricum trichordon’ ne différait pas énormément de celui des roues des horloges à pendule triangulaire qui leur succédèrent. Comparez le deuxième alinéa de la p. 513.
-
voetnoot1)
- J. van Ceulen (voir sur lui la note 4 de la p. 509 qui précède) n'était nullement dépourvu de biens. Mais il était sans doute ‘een man van weijnigh vermogen’ en comparaison avec les riches négotiants d'Amsterdam.
-
voetnoot2)
- Dans la lettre inconnue du 29 août, dont il est question dans la lettre de Hudde à Huygens du 3 septembre: voir la p. 24 du T. IX.
-
voetnoot3)
- Mentionné aussi aux p. 27, 31 et 579 du T. IX.
-
voetnoot5)
- Il s'agit de Johannes de Graaf: voir la Pièce IV qui suit (non pas d'Isaak de Graaf - T. IX, p, 27, note 3 -, comme nous l'avons déjà remarqué dans la note 1 de la p. 266 du T. IX).
|


 chronus est per parabolam BR cylindro applicatam cujus ½ latus rectum ABGa naar voetnoot3).
chronus est per parabolam BR cylindro applicatam cujus ½ latus rectum ABGa naar voetnoot3).