Logo DBNL
Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695 (1934)

Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695

(1934)–Christiaan Huygens–rechtenstatus Auteursrecht onbekend

Vorige Volgende

De Hugeniana centri oscillationis determinatione controversia ulterior.

La ‘De Hugeniana Centri Oscillationis Determinatione Controversia’, telle qu'on la trouve dans les éditions de 's Gravesande de 1724 et 1751 - nous y ajoutons le mot ‘ulterior’, puisqu'il s'agit en somme d'une continuation de la discussion entamée par Roberval (objections 13 et 14) - se compose de douze Pièces qui ont toutes été publiées dans nos Tomes VIII et IX, savoir six de Catelan, deux de Jacques Bernoulli, une du marquis du l'Hôpital et trois de Huygens1). Ces dernières Pièces,

quoiqu'elles affectent la forme de lettres adressées à un éditeur, ou de remarques sur une lettre de ce genre, font évidemment partie des Oeuvres proprement dites de Huygens. Nous pourrions donc, comme nous l'avons fait au T. XVI (p. 169-186) pour l'‘Extrait d'une lettre sur les règles du mouvement dans la rencontre des corps’, réimprimer ici les trois pièces de Huygens, auxquelles il faudrait bien joindre les neuf autres1) et les pourvoir d'un avertissement, de notes et d'appendices. Une treizième Pièce qu'il conviendrait d'y ajouter (pour ne rien dire des Nos 2259 et 2166 du T. VIII et 2580, 2581, 2587, 2594, 2597, 2598, 2600, 2603 et 2604 du T. IX) est le No 2690 (T. X, p. 114, J.B. ‘Demonstratio Centri Oscillationis ex Natura Vectis, etc.’), travail de Jacques Bernoulli publié dans les Acta Eruditorum de juillet 1691. Une quatorzième et une quinzième, datant de 8 et 9 ans après la mort de Huygens, viendraient s'y joindre tout naturellement, savoir la ‘Démonstration générale du centre de balancement ou d'oscillation, tirée de la nature du levier’ que Jacques Bernoulli publia en 1703 dans l'‘Histoire de l'Académie des Sciences de Paris’ et la ‘Démonstration du Principe de Mr. Huygens touchant le centre de balancement’, de 1704 (Hist. de l'Ac. d. Sc. de Paris) du même auteur. L'addition d'une seizième, savoir un chapitre du ‘Discours sur les Loix de la Communication du Mouvement’ de 1727 de Jean Bernoulli - comparez la p. 466 qui suit -2), ne serait nullement déplacée. Nous avons déjà parlé (p. 442) d'une section de la ‘Mécanique analytique’ de 1788 de Lagrange qui se rattache à ces disputes.

Au lieu de réimprimer les douze Pièces et celles que nous pourrions y ajouter, nous

nous contenterons toutefois d'y renvoyer le lecteur et de ne donner qu'un aperçu de la controverse.

 

Les mauvaises objections de Catelan, auteur de peu de mérite3), ont conduit des savants de plus de valeur, et Huygens lui-même, à considérer dans le cas des pendules linéaires le gain ou la perte de vitesse des différents points pesants qui résulte de leur réunion en un tout, lorsqu'on les attache à une barre, ou à un fil, linéaire et impondérable. De cet assemblage chaque point pesant situé au-dessus du centre d'oscillation se mouvrait plus vite, et chaque point situé au-dessous de lui plus lentement, s'il était seul attaché au point de suspension. En d'autres termes: la partie inférieure du pendule retarde le mouvement de la partie supérieure, cette dernière avance celui de la partie inférieure. Ne serait-il pas possible de calculer la place du centre d'oscillation en partant de la considération de ces gains ou pertes de vitesse? Ne pourrait-on donc pas se passer de l'Hypothèse I de la Pars Quarta appliquée anx points pesants se détachant les uns des autres à un moment donné?

Durant la vie de Huygens les chercheurs engagés dans cette voie - c.à.d. Catelan, Jacques Bernoulli, de l'Hospital et Huygens - se sont bornés à la considération de pendules linéaires. Ce n'est que vers 17034) que Jacques Bernoulli réussit à s'élever

à celle des corps oscillants de forme quelconque. Durant la vie de Huygens l'Hypothèse I de la Pars Quarta est donc restée la seule qui permît de trouver la formule générale pour le centre d'oscillation.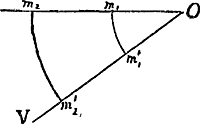



illustratie
[Fig. 2.]


Dans son article de 1681, Pièce I de la note 1 de la p. 457, Catelan considère deux points pesants égaux (m1 et m2) formant deux pendules simples ayant O [Fig. 2] pour axe d'oscillation. Ces points, réfléchis sans perte de vitesse par le plan OV, remontent à la hauteur d'où ils sont tombés; il en sera donc de même de leur centre de gravité commun. Mais il n'en sera plus de même, pense-t-il, lorsqu'on forme un pendule composé en réunissant les deux points pesants par un lien rigide et impondérable. Les vitesses des deux points, arrivés dans la position m′1 m′2 seront alors proportionnelles à leurs distances du point O; de plus, pense-t-il, la vitesse moyenne sera la même que dans le cas précédent. On a donc deux équations permettant de calculer les vitesses. Et si l'on suppose qu'à l'instant où le pendule composé atteint le plan OV, le lien se rompt, et que les points réfléchis s'élèvent jusqu'à ce que leurs vitesses soient épuisées, on peut calculer que le centre de gravité atteint une hauteur supérieure à celle dont il était tombé.

L'hypothèse gratuite d'après laquelle la vitesse moyenne des deux poids, lorsqu'ils atteignent le plan OV, est la même dans les deux cas considérés, provient peut-être de ce que l'auteur songeait à la constance que le produit ∑mw (donc aussi ∑v pour des quantités de matières égales) possède d'après Descartes dans le cas de collisions de différents corps. Il est vrai que suivant Descartes lui-même ce principe n'est nullement applicable dans le cas considéré. Mais nous pouvons avec de l'Hospital considérer Catelan comme ‘abusant de la pensée de Mr. Des Cartes, que la mesme quantité de mouvement se conserve toujours dans la nature’. (T. IX, p. 402).

 

Dans sa première réponse de 1682 (Pièce III) Huygens se borne à faire remarquer que l'expérience ne confirme pas tous les résultats qu'on peut tirer de la théorie de l'abbé de Catelan. C'est dans sa deuxième réponse de 1684 seulement (Pièce VIII) qu'il observe que le résultat du calcul de Catelan est ‘contre le grand Principe des mechaniques’, et il ajoute: ‘& si Mr. l'Abbé peut faire en sorte que [son Principe] soit vray, il aura trouvé le mouvement perpetuel. Son Principe estant donc faux puisqu'il meine à une fausse conclusion, il n'en peut rien inferer contre ma proposition qui ne soit faux aussi’.

 

Jacques Bernoulli, qui était déjà intervenu en 1684 dans le débat (Pièce VII) tâcha, sans beaucoup de succès, de préciser la question des gains et pertes de vitesse (Pièce X de 1686). Il remarque que dans le cas de la Fig. 2 le pendule (dans la posi-

tion horizontale p.e.) peut être considéré comme une balance qui n'est pas en équilibre et que les poids attachés au fléau impondérable doivent consumer une partie de leur vitesse ‘in premendo axe’. Les excès de vitesse, pense-t-il, pourraient se distribuer suivant une loi analogue à celle du levier. Il exhorte donc les savans ‘ut examinent, qualem legem communicationis celeritatum observent corpora mota, quae ex una parte innituntur firmo fulcimento, ex altera alio corpore itidem sed tardius moto’. Pense-t-il vraiment qu'il n'est pas certain que le centre de gravité, dans les conditions du problème [Fig. 2], doit monter à une hauteur aussi grande que celle dont il est descendu? Il semble bien qu'oui, car il propose, provisoirement il est vrai, une solution différant de celle de Catelan mais conduisant également, comme il le fait voir, pour les poids réfléchis à une hauteur du centre de gravité non égale à la hauteur primitive.

 

Pour pouvoir soutenir la possibilité de solutions différant de celle de Huygens tout en niant celle du mouvement perpétuel, il a recours à l'argument suivant: ‘Antequam finiam, in favorem Dn. Catelani hoc monebo, quod etiamsi commune gravitatis centrum juxta illum altius ascendere deberet, quam descendit, nondum tamen sequatur repertum fore motum perpetuum, ut sibi persuadet Ill. Hugenius, quoniam in istis abstrahi solet ab aëris resistentia, a diminutione celeritatis, quae necessario sequitur disruptionem vinculi, quo connectebantur partes penduli aliorumque obstaculorum’. Objection à laquelle Huygens répond avec beaucoup de sens (Pièce XII): ‘Mr. Bernoulli ne demeure pas d'accord de cette consequence, à cause de l'obstacle de l'air et quelques autres, qui en empêcheroient l'effet. Mais il devroit avoir considéré, que la hauteur qu'acquiert le centre de gravité par dessus celle qu'il avoit, estant toûjours une quantité determinée, & l'effet des obstacles n'estant pas determiné, & se pouvant diminuer de plus en plus, on pourroit facilement faire une machine, où l'avantage du rehaussement du centre de gravité surpasseroit l'empêchement des obstacles. Mais c'est de quoy assurément on ne sera jamais obligé de venir à l'épreuve’.

 

Consultez aussi, à propos de la question du mouvement perpétuel, le Pièce de Huygens qui suit sur la conservation des forces (p. 477), ainsi que notre Avertissement sur ce sujet.

 

Le marquis G.F. de l'Hospital répondit en 1690 à l'appel de Jacques Bernoulli par une lettre (Pièce XI) où il approuve son idée fondamentale et montre qu'il ne serait pas, dans sa considération d'une ‘balance’ chargée de deux points pesants, arrivé à un résultat erroné - car de l'Hospital considère la formule de Huygens pour la longueur du pendule isochrone comme certainement correcte - s'il avait parlé des accroissements infiniment petits des vitesses, et non pas des vitesses acquises après un temps fini. De l'Hospital le fait voir en considérant deux poids égaux. Il ajoute toutefois que le même raisonnement est applicable au cas de deux poids inégaux; il

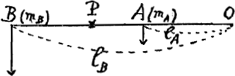illustratie faut considérer alors des excès d'accroissements de quantités de mouvement. De l'Hospital a raison, comme le montre le calcul suivant.

Les points pesants A et B [Fig. 3] acquièrent pendant un temps infiniment petit de durée déterminée les quantités de mouvement infiniment petites mAv et mBv respectivement, lorsqu'ils ne sont pas réunis l'un à l'autre. Lorsqu'ils le sont, le poids A n'acquiert que la quantité de mouvement mA vA, où vA est inconnue. L'excès qui doit être distribué sur le poids B et sur l'axe O, est donc mA (v - vA).

B en obtiendra la part lA/lB mA (v - vA) s'il est vrai que les excès se distribuent suivant la loi du levier. B aura donc la quantité de mouvement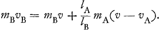

illustratie

Or, en vertu de la liaison vA : vB = lA : lB.

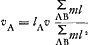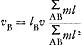On a donc illustratie et illustratie.

Le centre d'oscillation P, situé à une distance LAB de l'axe O, doit être tel qu'en ce point la barre impondérable acquiert précisément la vitesse v. Il faut donc qu'on ait vA : v = lA : LAB.

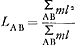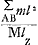Donc illustratie ou illustratie; M y représente la somme des quantités de matière mA et mB, et lZ la distance à l'axe de leur centre de gravité.

 

S'il y a trois points pesants A, B et C, il faut, dit de l'Hospital, considérer deux d'entre eux comme réunis dans leur centre d'oscillation. L'exemple numérique qu'il propose fait voir que cette règle doit être entendue comme suit.

Le poids C donne un excès de quantité de mouvement mC (v - vC). Il faut, pour calculer vC, distribuer cet excès sur l'axe O et sur le point P, centre d'oscillation des points A et B. Le centre P reçoit donc la quantité lC/LAB mC (v - vC) et lorsqu'on

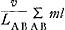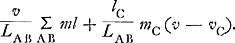ajoute cette quantité à celle que les points A et B possédaient déjà d'après le calcul précédent (c.à.d. mAvA + mBvB ou illustratie), on obtient la quantité totale

illustratie

Les points A et B ont maintenant, grâce à la liaison, les vitesses vA = lA/lC vC et vB = lB/lC vC respectivement.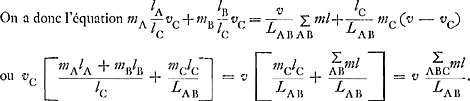



illustratie

On en peut tirer 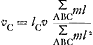illustratie, d'où résultent aussi les vitesses vA et vB. On en conclut, en raisonnant comme dans le cas de la Fig. 2, que 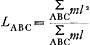illustratie.

Et l'on obtient une formule analogue - c'est toujours la formule générale de Huygens pour le cas des pendules linéaires - en ajoutant encore'un quatrième poids, etc. De l'Hospital dit donc à bon droit ‘que cette methode est generale, quel que soit le nombre des poids, & quelque inégalité qu'ils ayent entre eux’.

Mais quel lecteur, de nos jours, considérera ce raisonnement comme convaincant? Quelle raison de l'Hospital peut-il avoir eue de croire à la justesse du résultat obtenu, si ce n'est que ce résultat s'accorde avec celui trouvé suivant la méthode de Huygens? C'est cette concordance seule qui lui permet de dire: ‘Il est aisé de conclurre de tout cecy, que le principe de Mr. Bernoulli est veritable’. Considéré en lui-même ce principe, tel que de l'Hospital le formule, est si peu évident qu'avant d'avoir fait le calcul on le jugerait plutôt erroné.

 

Huygens dans ses ‘remarques sur la lettre précédente & sur le récit de Mr. Bernoulli dont on y fait mention’ (Pièce XII, de 1690) a la politesse de ne point attirer l'attention sur la plus grande généralité de sa propre solution. Quoi que la démonstration du marquis, dit-il, ‘ne laisse pas de comprendre plusieurs choses qui peuvent

d'abord faire de la peine aux Lecteurs’, il l'appelle ‘bonne & bien fondée’. Il rappelle cependant son principe et se contente de dire: ‘Je croy que c'est autant en cela que consiste la cause physique, de ce que dans le pendule composé les poids A & B estant descendus conjointement au bas de leur vibration, n'acquierent pas ensemble autant de vitesse, que s'ils estoient tombez separément des mêmes hauteurs; qu'en ce que le poids A consume une partie de son mouvement en agissant sur le point fixe, suivant la demonstration de Mr. Bernoulli & de Mr. le Marquis de l'Hospital’.

 

‘Cette analyse’, dit Lagrange1), ‘sit revenir Jacques Bernoulli sur la sienne,et donna enfin lieu à la première solution directe et rigoureuse du problème des centres d'oscillation’.

La solution de Huygens n'était-elle donc pas directe et rigoureuse?

Bernoulli d'ailleurs, lorsqu'il recommença ses efforts, suivit d'abord une méthode fort inférieure à celle de Huygens, et nullement plus parfaite que celle de l'Hospital. C'est sans doute pour cette raison que Huygens n'a plus jugé nécessaire de prendre part à la discussion.

Dans les Acta Eruditorum de 1691 (notre T. X, p. 214) Bernoulli propose de distribuer, lorsqu'il y a plus de deux points pesants, l'excès de l'accroissement de la quantité de mouvement de chaque point entre l'axe et le poids extrême!2). Ce singulier principe conduit encore une fois au résultat exact - pour une série de points situés en ligne droite bien entendu - mais c'est uniquement le succès, nous semble-t-il, qui le justifie dans une certaine mesure.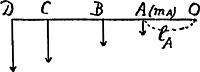



illustratie
[Fig. 4.]


Considérons un pendule [Fig. 4] chargé de quatre poids mA, mB, mC, mD.

Soit g l'accélération de la pesanteur, jA, jB, jC, jD les accélérations que les quatre poids ont réellement en partant du repos dans la situation indiquée. Par unité de temps le point A doit céder l'excès mA (g - jA). Suivant l'hypothèse le poids extrême D en reçoit la quantité mA lA/lD (g - jA).

Ce poids reçoit donc en tout la quantité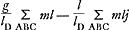 illustratie, et cet accrois-
sement de quantité de mouvement par unité de temps doit être égal à l'accroissement mD (jD - g). Egalant ces deux expressions, on trouve 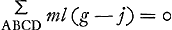illustratie.

Cette équation exprime que la somme des moments des excès des accroissements des quantités de mouvement (disons plus brièvement: la somme des moments des excès des forces) autour du point O est nulle; mais une équation ou un énoncé de ce genre ne se trouve pas encore dans l'article de Bernoulli.

En vertu de la liaison, j doit être proportionnelle à l. Donc j = Cl, où C est une constante. L'équation trouvée devient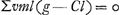 illustratie, donc C = g ∑ml/∑ml2.

Mais la distance L du centre d'oscillation à l'axe doit être telle qu'on ait g = Cl. Il en résulte encore une fois L = ∑ml2/∑ml.

L'auteur a absolument tort, nous semble-t-il, en ajoutant: ‘Haec vero centri oscillationis demonstratio sic reformata, uti generalis est et facilis, inque Geometrica exactitudine Hugenianae neutiquam cedit, sic eidem in eo praeferenda videtur, quod principium vectis, quo nititur, indubitatum est ac evidens, cum Hugeniana hypothesis obscura fere sit, nec aliam ob causam pro vera habeatur, quam quod nihil in contrarium afferri potest, intellige in solidis corporibus’3).

Leibniz en janvier 1692 (T. X, p. 229) dit à bon droit que ‘Mr. Bernoulli a des pensées un peu embarassées sur le centre d'oscillation’.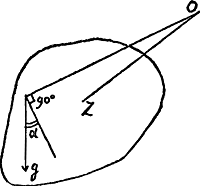



illustratie
[Fig. 5.]


Ce n'est que dans son article de 1703, déjà cité à la p. 458 qui précède, que Jacques Bernoulli parvint à formuler généralement le principe qui ramène, en un certain sens, le problème considéré à un problème de statique, préparant ainsi la voie à d'Alembert. Suivant ce principe 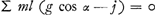illustratie [Fig. 5], où la somme ou intégrale des moments est étendue à tous les points du pendule. Nous désignons par j l'accélération réelle dans le sens du mouvement. Quoique Bernoulli n'applique ce principe qu'au cas d'un pendule de forme symétrique, on doit dire

qu'il a trouvé cette fois une méthode menant à la solution complète et qu'on peut juger équivalente à celle de Huygens. Mais en nous étendant sur cette matière, nous franchirions les limites qui conviennent à cette publication.

 

Le lecteur a déjà fait connaissance avec les réflexions de Huygens de 1692 ou 1693 qui constituent notre Appendice VI à la Pars Quarta de l'‘Hor. osc.’ (p. 433 qui précède). Dans cette Pièce qui n'a pas vu le jour, les ‘vires acquisitae’, proportionnelles au carré de la vitesse, jouent un plus grand rôle que dans la Pars Quarta.

Dans le Chap. XIV de son travail de 1727 (voir la note 2 de la p. 458 qui précède) - ce n'était d'ailleurs pas la première fois qu'il s'occupait de ce sujet - Jean Bernoulli trouve la place du centre d'oscillation - en se bornant an cas du pendule linéaire, ce qui n'était nullement nécessaire - en partant du principe que ‘la pesanteur produit dans la somme des poids une quantité déterminée de force vive, de quelque manière qu'ils descendent’, en d'autres termes ‘que la somme des forces vives des poids est le même après que les poids sont descendus aussi bas qu'ils le peuvent, soit que ces poids descendent conjointement attachés à une même ligne inflexible [disons plus généralement: soit que ces poids, ou points pesants, soient réunis en un assemblage rigide], soit que chacun de ces poids descende librement, comme un pendule simple’. Ceci peut aisément être déduit du principe de Huygens et n'est en somme qu'une autre manière d'exprimer ce principe. Jean Bernoulli nous paraît avoir tort en disant ‘que le principe qu'employe M. Huygens, & qu'il propose comme un axiome, étoit un peu trop hardi’, mais qu'on ne se sert nullement de ‘principes qui ne paraissent pas toujours assez naturels’ lorsqu'on ‘déduit de la seule conservation des forces vives, la détermination du centre d'oscillation’.


Vorige Volgende