Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695

[p. 419]

Appendice III
À la pars quarta de l'Horologium oscillatorium’.
[1669-1670.]¹⁾

[Fig. 152.]

[Fig. 153.]

§ 1. Si circulus vel circulisector in particulas minimas aequales divisus intelligatur a quibus singulis rectae ad centrum ductae sint. Erunt harum omnium quadrata simul sumta aequalia dimidio quadrato radij, multiplici secundum particularum ipsarum numerum.

Sit Circulus [Fig. 152] in annulos aequalis latitudinis divisus. Et annuli omnes in particulas aequales, adeo ut in unoquoque sit numerus particularum pro ratione magnitudinis annuli²⁾. Triangulum EGG [Fig. 153] lineis basi parallelis dividatur in segmenta annulis proportionalia. Et segmenta omnia divisa in particulas aequales inter se, non opus autem ut et particulis circuli aequales sint. Sit vero numerus particularum in segmento GG idem qui in annulo DD. Unde necessario et in reliquis deinceps segmentis erunt numeri ijdem qui in annulis ipsis respondentibus, et in toto proinde ∆^lo EGG idem numerus particularum qui in circulo AB.

EF [Fig. 153] ∞ AB [Fig. 152]. GG ad arbitrium, KE parallela GG.

GG secta in tot particulas inter se aequales quot sunt in annulo DD. Ergo quadrata omnia LM aequalia quadratis omnibus ex annulo D in A ductarum. Et quadrata a distantijs particularum segmenti HH ab KE [Fig. 153], aequalia omnibus quadratis EA [Fig. 152] &c. Atqui summa quadratorum a distantijs particularum trianguli EGG aequatur rectangulo OEN³⁾, multiplici secundum particularum numerum.

1) Cet Appendice est emprunté aux p. 245-249 du Manuscrit D. La p. 235 porte la date du 21 nov. 1669 et la p. 250 (comparez la note 1 de la p. 388 du présent Tome) celle du 9 janvier 1670. Nous divisons cette Pièce en §§.

2) Comparez le troisième alinéa de la p. 443 du T. XVI.

3) N est le centre de gravité du triangle, EO la subcentrique de l'onglet obtenu en coupant le prisme élevé sur le triangle par un plan oblique passant par KK. EN × NO est le ‘rectangulum distantiarum’ par rapport au centre de gravité quî doit être augmenté de EN² (de sorte qu'on obtient EN × OE) lorsque le point de suspension est en E. Voir p.e. la partie B de l'Appendice précédent.

[p. 420]

posita EN ⅔ EF, et EO ¾ EF, unde ▭ OEN ∞ ½ qu. EF. Ergo et summa quadratorum a distantijs particularum circuli AB a centro A aequabitur ½ qu. EF sive ½ qu. AB multiplici secundum particularum numerum qui sunt in triangulo vel in circulo¹⁾.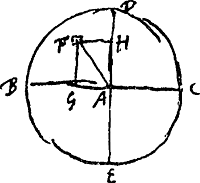

[Fig. 154.]

Si circulus in particulas minimas aequales divisus intelligatur, et a singulis in diametrum circuli perpendiculares duci. Erunt harum omnium quadrata simul sumta aequalia quartae parti quadrati radij, multiplici secundum numerum particularum.

Sit circulus [Fig. 154] centro A diametro BC, et diviso cogitatione plano ejus in particulas minimas aequales. sint ab ijs singulis ductae in diametrum BC perpendiculares sicut a particula F ducta est FG. dico harum omnium perpendicularium quadrata aequari ¼ qu. AB mult. s.n.p.

Sit enim ducta altera circuli diametrus ipsi BC ad angulos rectos DE et in eam cadat perpendicularis FH et jungatur FA. Sunt igitur quadrata FG et FH simul aequalia quadrato FA. Eademque ratione quadrata bina perpendicularium quae ab unaquaque particula ducuntur ad diametros BC, DE, aequalia esse constat quadrato distantiae ejus particulae a centro A. Et quadrata omnia a distantijs particularum a diametris BC, DE aequalia omnibus quadratis distantiarum a centro A. Atqui quadrata perpendicularium omnium ad diametrum BC aequari liquet quadratis omnibus perpendicularium ad diametrum DE. Ergo quadrata perpendicularium omnium ad diametrum unamquamque BC vel DE aequantur semissi quadratorum a distantijs particularum a centro A. hoc est per praec. ¼ qu. radij AB multiplici s.n.p. quod erat demonstrandum.

§ 2. Si sphaera [Fig. 155] vel sector sphaerae in particulas minimas aequales dividi intelligatur, a quibus singulis ad centrum sphaerae rectae ducantur. Erunt harum

1) Ceci peut s'écrire en notations plus modernes

[p. 421]

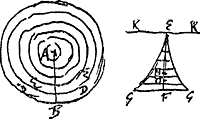omnium quadrata simul sumta aequalia ⅗ quadrati radij multiplicibus sec. p. n.

Sit sphaera primum divisa in involucra sphaerica minimae et aequalis crassitudinis omnia circa idem centrum ordinata, et haec deinde secta in particulas aequales, quarum in unoquoque involucro multitudo erit pro ratione magnitudinis, deinde accepta EF aequali radio AB, constituantur ad eam bina complementa ½ parabolarum verticem habentium E punctum axem vero EK quae ipsi FE perpendicularis ducatur. figura autem ex istis composita EGG secetur totidem lineis basi GG parallelis et aequalibus interstitijs a se invicem remotis quot sunt superficies sphaeram in involucra dirimentes. Sitque segmentum GG divisum in partes aequales totidem quot sunt in involucro sphaerico DD, itemque reliqua segmenta figurae EGG secta sint in ejusdem magnitudinis particulas ijs quae in segmento GG. Ergo cum involucra sphaerica sint sicut quadrata suorum radiorum, et segmenta quoque figurae EGG sint ut quadrata distantiarum suarum ad recta EK. patet segmenta involucris proportionalia esse si eodem in ordine sumantur. Unde unicuique etiam segmentorum idem inerit numerus partium qui involucro ipsi respondenti. Et si a singulis proinde particulis segmentorum ad rectam EK perpendiculares cadant, erunt quadrata a particulis cujusque segmenti eodem numero ac magnitudine cum quadratis a rectis quae a particulis involucri respondentis ducuntur ad centrum A. &c.²⁾.

2) En marge: ‘potest EGG conus poni de quo antea sit demonstratum’. Suivant la Prop. XXII de la Pars Quarta (Fig. 112 de la p. 329 qui précède) les sections d'une pyramide ou d'un cône de même hauteur r sont proportionnelles à celles de la figure plane EGG ici considérée. La somme cherchée est donc égale à celle des carrés des distances de toutes les particules du cône au plan de la base GG, évidemment en supposant que le cône contient le même nombre de particules que la sphère.
Son ‘premier rectangulum’ - voir sur ce terme la p. 48 de l'Avertissement - est alors 3/80 r² d'après le paragraphe ‘Centrum oscillationis coni’ de la Prop. XXII de la Pars Quarta. Pour obtenir la grandeur cherchée il faut y ajouter le carré de la distance du sommet au centre de gravité, c.à.d. 9/16 r². Comparez les calculs de l'Appendice précédent. On obtient alors la somme ⅗r². L'on pourrait dire (comparez la note 1) que Huygens a ainsi démontré la formule , ou encore qu'il a trouvé que le moment d'inertie d'une sphère homogène par rapport à son centre est ⅗ Mr², où M désigne la masse.

[p. 422]

Propositio.

Si sphaera in particulas minimas aequales divisa intelligatur, et a singulis in planum per centrum sphaerae ductum perpendiculares actae, erunt harum omnium quadrata simul sumta aequalia ⅓ quadratorum a distantijs omnium particularum a sphaerae centro, hoc est ⅕ quadrati radij multiplici sec. p. num.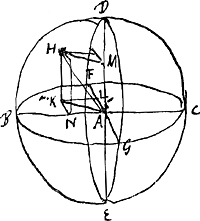

[Fig. 156.]

Sit sphaera [Fig. 156] cujus centrum A, sectio per centrum circulus BGCF, cujus diameter BC. et intelligantur a singulis sphaerae particulis perpendiculares ductae ad planum BGCF. sicut a particulis H ducta est HK. dico &c.

Secetur enim sphaera alio plano per diametrum BC, quod sit priori BGCF ad angulos rectos. Itemque tertio plano DGEF quod sit rectum ad utrumque jam dictorum faciens in circulo BGCF sectionem GF, et in circulo DBEC sectionem DE. Et a puncto K ducantur ad BC, FG perpendiculares KN, KL, et jungantur KA, HA. Est igitur quadratum HA aequale quadratis HK et KA. Sed quadratum KA aequale quadratis KN, NA, sive quadratis KN, KL. Ergo quadratum HA aequale quadratis tribus HK, KN, KL. Est autem KN aequalis perpendiculari quae a puncto H duceretur in planum DBEC, et KL aequalis perpendiculari quae duceretur ab eodem puncto H in planum DGEF. Ergo quadrata tria HK, KN, KL seu quadratum HA aequale quadratis distantiarum particulae H a tribus planis quibus sphaeram per centrum secuimus. Eademque ratione erit quadratum distantiae uniuscujusque particulae à centro A aequale quadratis distantiarum ejus particulae a tribus dictis planis, et proinde quadrata omnium distantiarum a centro A aequalia quadratis omnibus perpendicularium a particulis in tria plana per centrum sphaerae ducta. Atqui manifestum est quadrata omnium perpendicularium in quodlibet trium planorum simul sumta eandem efficere quadratorum summam. Ergo summa perpendicularium in unum horum planorum velut BGCF aequatur ⅓ quadratorum à distantijs omnium particularum a centro A. hoc est, per praec. ⅕ quadrati radij multiplici sec. num. part. in quas sphaera divisa intelligitur. quod erat demonstrandum.

Propositio.

Posita sit prius sphaera in particulas divisa. si ab omnibus ducantur perpendiculares in axem ejus, erunt harum omnium quadrata aequalia ⅔ quadratorum a distantijs particularum a centro sphaerae, hoc est ⅖ quadrati radij multiplicibus sec. num. part.

[p. 423]

In eadem figura sit HM perpendicularis a particula H in axem DE, eodemque modo a singulis particulis in eundem axem perpendiculares ductae intelligantur, caetera vero constructa sint ut prius. Est ergo HM aequalis KA, cujus quadratum aequale quadratis KN, KL, quare et quadratum HM aequale quadratis KN, KL, hoc est quadratis perpendicularium a puncto H ductarum in planum DBEC, DGEF. Eademque ratione quadratum perpendicularis ab unaquaque particula in axem DE, aequale ostendetur quadratis perpendicularium ejus particulae a planis ijsdem duobus. Unde patet quadrata omnia perpendicularium a singulis sphaerae particulis in axem DE ductarum aequari quadratis omnibus perpendicularium ab ijsdem particulis ductarum in plana DBEC, DGEF. Sunt autem quadrata perpendicularium a particulis omnibus in alterutrum horum planorum ductis aequalia quadratis perpendicularium ab omnibus ijsdem particulis ductarum in reliquum planum. Ergo quum, ex praec. sit summa ista quadratorum in unum planum aequale parti quintae quadrati radij AB multiplici s.n.p. Erunt duae summae quadratorum a perpendicularibus particularum in duo plana DBEC, DGEF, hoc est, summa quadratorum a perpendicularibus quae in axem DE ducuntur ab omnibus particulis aequalis ⅖ quadrati AB multiplicibus s.n.p. quod erat demonstrandum.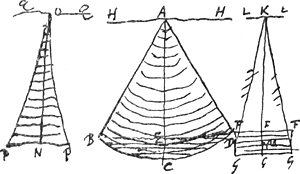

[Fig. 157.]

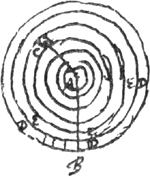
§ 3. In sphaerae sectore quoque centrum oscillationis inveniri potest constituta ad latus figura plana proportionali quae ex complemento parabolae ad circumscriptum rectangulum et segmento item parabolae conflata erit¹⁾. in qua figura invenire licet omnia quibus ad solutionem problematis opus est. Sed alia ratione multo breviori atque hic peculiari res conficietur hoc modo.

Sit [Fig. 157] sector ABCD, ex sphaera cujus centrum A. axis vero sectoris sit AC

1) La partie supérieure de cette figure a latere, composée, comme celle de la Fig. 155, de deux ‘complementa parabolae’, correspondrait évidemment à la partie conique du secteur de sphère, tandis que la partie parabolique inférieure correspondrait au segment de la sphère qui termine le secteur (comparez la p. 470 du T. XVI ou plutôt la p. 331 qui précède).

[p. 424]

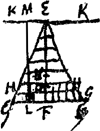
suspendique intelligatur ab axe horizontali per A punctum ducto. Itaque invenienda est summa quadratorum a distantijs particularum singuli sectoris ab axe illo. sive summae duae distantiarum a plano horizontali AH, et a plano per axem sectoris AC ducto. Hae enim divisae¹⁾ per distantiam quae est à suspensione A ad centrum gravitatis sectoris multip. s.n.p. dabit distantiam centri oscillationis ab eadem suspensione A.

Ut ergo primum inveniatur summa quadratorum a plano horizontali AH. intelligatur sector divisus superficiebus sphaericis aequali intervallo distantibus et quarum omnium centrum idem A, fietque ut involucra sphaerica hoc modo formata eandem habeant inter se rationem quam quadrata radiorum suarum sphaerarum utque in singulis involucris pro ratione magnitudinis numerus particularum minimarum contineatur.

Quod si vero involucrum ejusmodi, puta extremum BCF secetur planis horizontalibus aequaliter inter se distantibus, scindetur ijs involucrum in partes aequales aeque ac sphaerica superficies, de qua ex Archimede facile hoc ita se habere ostendetur²⁾. Itaque figura uni isti involucro proportionalis a latere ponenda erit rectangulum FG, parem involucro altitudinem habens adeo ut si ▭ hoc in totidem particulas aequales sectum intelligatur ac involucrum BCD quadrata a distantijs earum ab recta LL quae eadem sit altitudine cum plano HH, aequalia futura sint quadratis distantiarum particularum involucri BCD a plano HH. Sunt autem quadrata distantiarum particularum ▭ⁱ FG ab KL aequalia 1/12 quadrati altitudinis FG³⁾ una cum quadrato MK (posito scilicet M centro gravitatis ▭ⁱ FG) multiplicibus per numerum particularum ipsius rectanguli. ergo et quadrata a distantijs particularum involucri BCF aequantur 1/12 quadrati FG et quadrato MK, multiplicibus sec. num. part. ▭ⁱ FG sive sec. num. part. ipsius involucri BCD. Sit recta NO quae possit⁴⁾ quadratum MK cum 1/12 quadrati ab FG. Et constituantur ad ipsam NO complementa semiparabolarum ONP quarum vertices ad O, figuraque ab his composita secetur rectis basi NP parallelis, quae dividant axem NO in partes totidem aequales quot sunt in axe AC factae a superficiebus sphaericis. unde quidem segmenta figurae OPP proportionalia erunt involucris sphaericis sectoris ABCD. Et si figura OPP in totidem particulas minimas aequales quot sector divisa intelligatur, erunt earum particularum totidem comprehensae segmento imo PP quot sunt in involucro imo BCD. et in reliquis item segmentis singulis idem numerus particularum qui in involucris ordine ipsis respondentibus.

1) Il s'agit de la somme des ‘summae duae’. C'est pourquoi Huygens met le verbe au singulier.

2) La proportionnalité de deux calottes sphériques, faisant partie de la même surface sphérique, avec leurs hauteurs découle aisément de la Prop. XLII du Livre I ‘De Sphaera et Cylindro’ d'Archimède, suivant laquelle chaque calotte est égale au cercle dont le rayon est la distance du point central de la calotte à un point de son contour.

3) 1/12 FG², produit de ½ FG par ⅙ FG, est le ‘premier rectangulum’ du rectangle; il faut y ajouter MK² pour obtenir la grandeur cherchée. Comparez la note 2 de la p. 421.

4) C.à.d. dont le carré est égal à ...

[p. 425]

Quia autem quadrata omnia distantiarum particularum involucri BCD à plano HH aequalia ostendimus quadrato MK + 1/12 quadrati FG multiplicibus sec. n. partic. involucri ipsius. Ergo et quadrata eadem distantiarum aequalia quoque erunt quadrato NO multiplici secundum num. part. segmenti PP. hoc est quadratis omnibus a distantijs particularum segmenti PP ab recta OQ basi figurae parallela. Eademque ratione quadrata à distantijs particularum quae in singulis involucris à plano HH aequalia erunt quadratis a distantijs particularum segmenti respondentis figurae OPP ab recta OQ. Quamobrem cum summa quadratorum a distantijs omnium particularum figurae OPP ab recta OQ aequetur ⅗ quadrati ON, sicut cum de pyramide ageremus ostensum est⁵⁾, etiam summa quadratorum a distantijs omnium particularum sectoris ABCD a plano HH aequabitur ⅗ quadrati ON.

Dicatur radius AC a; EC vel FG b, altitudo nempe superficiei sphaericae BCD. Quia ergo qu. ON aequale fecimus qu. KM quae est a - ½b et 1/12 qu. FG sive b. Erit qu. ON aequale aa - ab + ⅓bb, cujus tres quintae sunt ⅗aa - ⅗ab + ⅕bb. quibus proinde multiplicibus per num. part. sectoris sphaerici ABCD aequalia erit dicta summa quadratorum a distantijs omnium particularum sectoris ejusdem a plano AH.

Jam porro quadrata distantiarum a plano per axem sectoris AC invenienda essent. Sed eorum summa facile investigabitur ex summa jam inventa quadratorum a distantijs a plano AH et ex summa cognita quadratorum a distantijs a centro A, quae aequalia sunt ⅗ qu.ⁱ AC multiplicibus sec. num. p. sectoris⁶⁾. Nam si a singulis his quadratis à distantia alicujus particulae a centro A auferantur singula illorum quae fiunt a distantia ejusdem particulae a plano AH, manifestum est relinqui singula quadrata distantiae ejusdem particulae ab axe AC. ac proinde si a summa quadratorum distantiarum a centro A, hoc a ⅗aa, auferatur summa quadratorum a distantijs à plano AH, hoc est ⅗aa - ⅗ab + ⅕bb, relinquetur summa quadratorum a distantijs omnibus ab axe AC, quae erit ⅗ab - ⅕bb. Hujus vero summae quadratorum à distantijs ab axe, semissis est summa quadratorum a distantijs a plano per axem AC, ut facile intelligitur ex ijs quae de circulo ostendimus prop...⁷⁾ si nempe sector totus in segmenta circularia dividi intelligatur. Ergo summa quadratorum a distantijs a plano per axem erit 3/10 ab - 1/10 bb. quibus additis ad summam supra inventam quadratorum a distantijs a plano AH, nempe ⅗aa - ⅗ab + ⅕bb, fit summa quadratorum a distantijs ab axe oscillationis per A punctum ducto, ⅗aa - 3/10 ab + 1/10 bb. quae nempe multiplicia intelliguntur s.n. part. sectoris.

Applicando itaque planum aequale his ⅗aa - 3/10 ab + 1/10 bb ad intervallum inter

5) Comparez la note 2 de la p. 421.

6) D'après la première partie du § 1.

7) Il s'agit de la proposition qui constitue la deuxième partie du § 1 [Fig. 154].

[p. 426]

centrum A et centrum gravitatis sectoris, quod est ¾a - ⅜b¹⁾, fiet distantia centri oscillationis ab eodem centro A, 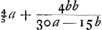, hoc est quatuor quintae radij, cum quatuor decimisquintis rectae cujusdam, quae sit ad sinum versum sectoris EC²⁾, sicut hic ad reliquam partem diametri sphaerae. Unde si pro sectore hemisphaera fuerit, erit haec distantia 16/15 a. Ut autem in alia quavis suspensione sectoris, dummodo ab axe qui sit aequidistans plano circuli BD, habeatur longitudo penduli isochroni, oportet a plano invento ⅗aa - 3/10 ab + 1/10 bb, auferre quadratum dictae distantiae ¾a - ⅜b, unde relinquitur 3/80 aa + 21/80 ab - 13/320 bb rectangulum distantiarum³⁾. quod nempe applicatum ad distantiam centri gravitatis ab axe oscillationis quolibet¹⁾ dabit intervallum quo centrum oscillationis inferius est centro gravitatis.

Quod autem diximus centrum gravitatis sectoris distare a centro A ¾a - ⅜b facile ostenditur diviso sectore ut fecimus in involucra concentrica, quorum singulorum centrum gravitatis altitudinem ipsorum bifariam dividit⁴⁾.

1) C.à.d. en divisant la première grandeur par la deuxième.

2) La flêche EC ou b constitue le ‘sinus versus’ de l'arc BCD, donc aussi celui du secteur.

3) Comparez p.e. la note 3 de la p. 419 ou la note 2 de la p. 421.

1) C.à.d. en divisant la première grandeur par la deuxième.

4) Il résulte en effet de ce théorème sur le centre de gravité d'une calotte sphérique que le centre de gravité d'un secteur sphérique coïncide avec celui d'un cône de hauteur a - ½b dont le centre de la sphère constitue le sommet.