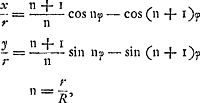Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695

[p. 399]

Appendice III
À la pars tertia de l'‘Horologium oscillatorium’.
1678.

[Fig. 139.]

§ 1¹⁾.

Omnis Epicyclicae evolutione similis Epicyclica describitur.

Ut radius circuli super quo revolutio ad diametrum circuli revoluti ita utriusque summa ad aliam; Haec juncta diametro circuli revoluti efficiet dimidiam longitudinem Epicyclicae ex revolutione descriptae. Vel curva Epicyclicae est ad diametrum circuli genitoris ut dupla diameter circuli manentis cum dupla diametro revoluti ad semidiametrum manentis.

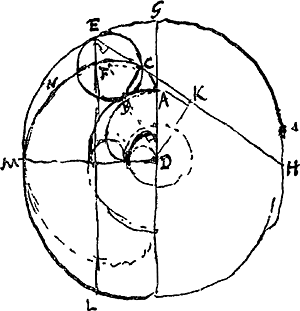
DA ∞ AG [Fig. 139]. arcus BC ∞ BA. punctum C in cycloide. DBE linea recta. ECH recta. EL parall. GD.

Dico EL esse ∞ EH. Et EC ∞ ¼EH.

Ducatur BC. et DK perp. EH. ∠ ECB est rectus. Ergo ut DE ad EB ita KE ad EC. Ergo EC ∞ ½EK sive ∞ ¼EH. Ducatur FC. quia jam radius FB ∞ ½ rad. AD et arcus BC ∞ BA, erit ang. BFC dupl. BDA. Ergo ∠ BEC ∞ BDA ∞ DEL. Ergo EH ∞ EL.

Hinc video MNCA curvam quae terminat spatium radiosum in speculo cavo MGH, a radijs axi DG parallelis, esse cycloidem a circulo EB, super duplo majoris diametri circulo AB revoluto²⁾.

1) Le § 1 - la division en §§ est de nous - de cet Appendice provient de la p. 164 du Manuscrit E. Voir sur la date le début du § 2. On trouve à la p. 164 quelques autres figures dans le genre des Fig. 139 et 140 que nous ne reproduisons pas. Les deux premières propositions du § 1 sont démontrées au § 2.

2) LE, rayon incident sur un miroir cylindrique, étant réfléchi suivant EH qui touche l'épicycloïde au point C, on peut en conclure que tous les rayons provenant de rayons incidents parallèles à LE la toucheront également. Comparez la p. 41 de l'Avertissement qui précède: dans son article de 1727 Krafft dit à tort: ‘Cum vero dubitaretur pluresne una possibiles sint hujus indolis nec ne [c.à.d. s'il existe d'autres courbes que la cycloïde où la développée et la développante sont pareilles]: non longe post Tschirnhusius Causticis fortasse suis probe intentus secundam invenit, Causticam nempe Semicirculi quae Epicyclois est, quam protulit deinde in Actis Lips. 1682, M. Novembri’.
Voir encore sur l'évolution et la courbure d'après Huygens la p. 183 du T. X.
L'hypocycloïde et sa développée semblable à elle-même furent considérées par Newton dans son ouvrage de 1687; voir les notes 5 de la p. 168 et 19 de la p. 514 du T. IX, ainsi que la note 000 de la p. 000 qui suit.

[p. 400]

§ 2¹⁾. 26 Nov. 1678.

lu a l'assemblée le 3 dec. 1678.

La mesure des lignes Epicycloides.

Mons. de Vaumesle Religieux de Normandie m'ayant mandè qu'il avoit trouvè la mesure de la ligne Epicycloide, lors que le cercle generateur et le cercle immobile sont egaux, cela m'a donnè occasion de chercher cette demonstration generale²⁾.

1) Les §§ 2 et 3 sont empruntés à deux feuilles détachées (f. 175 et 176) se trouvant dans le portefeuille ‘Chartae mathematicae’. Toutefois, sauf la première et la dernière phrase, et sauf quelques différences insignifiantes dans le texte, le § 2 se lit également à la p. 165 du Manuscrit E. Comme nous l'avons indiqué dans la note 6 de la p. 117 du T. VIII, les §§ 1-3 ont déja été publiés en 1833 (dans un ordre différent) par P.J. Uylenbroek dans les ‘Chr. Hugenii aliorumque seculi XVII virorum celebrium Exercitationes Mathematicae et Philosophicae, Hagae Comitum, Ex Typographia Regia’. Uylenbroek s'est servi, pour le § 2, du texte du Manuscrit E.

2) On trouve aux p. 115 et 125 du T. VIII les deux lettres de 1678 (resp. du 29 oct. et du 19 nov.) de de Vaumesle à Huygens. Elles furent suivies en juillet 1679 par une troisième lettre non moins intéressante (T. VIII, p. 189). Huygens connaissait déjà l'épicycloïde, quoiqu'il n'en eût apparemment pas encore considéré les propriétés; voir la note 6 de la p. 127 du T. VIII ainsi que les remarques publiées plus loin dans le présent Tome sur la forme des dents d'un engrenage.
Mons. A. Legoy, archiviste départemental à Saint-Lo, nous a fait savoir que d'après différentes liasses du fonds de l'abbaye d'Hambye ‘dom Pierre de Vaumesle’ fut prieur en 1698, 1704, 1705, 1707 et probablement jusqu'à 1711, lorsqu'un successeur fut élu. En 1690 Huygens lui donne déjà le titre de Presbyter (T. IX, p. 515). Il est mentionné comme religieux en différentes années, depuis 1676 jusqu'à 1691.

Propos. 1.

Par l'évolution de la moitiè d'une Epicycloide, en commencant par le sommet, il s'engendre la moitiè d'une autre Epicycloide semblable à la premiere³⁾.

3) Dans sa première lettre de Vaumesle dit déjà ‘que par leuolution de la cycloïde circulaire est decrite une autre cycloïde circulaire triple de la premiere’. Il ne considère que le cas où les rayons des cercles immobile et mobile sont égaux: sa ‘cycloïde circulaire’ est la cardioïde.

[p. 401]

[Fig. 140.]

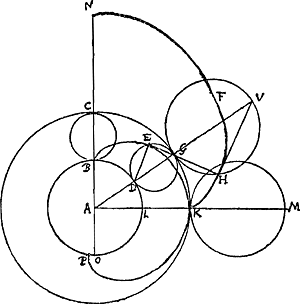
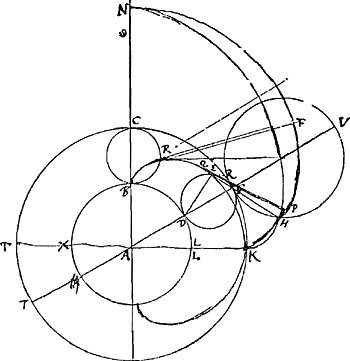
Soit BEK [Fig. 140] la moitiè d'une Epicycloide, descrite par le roulement du cercle BC sur le cercle immobile BL. Et le cercle KM estant supposè estre au cercle KC comme le cercle CB au cercle BL, soit, par le roulement du cercle KM sur le cercle KC immobile, descrit la demie Epicycloide KFN, qui sera terminée à la droite AB prolongée; et sera semblable a la demie Epicycloide BEK, à cause de la proportionalité des cercles.

Je dis que la mesme courbe KFN sera descrite par l'Evolution de la courbe BEK, commencée par K.

Car ayant pris dans BEK quelque point E, posons que le cercle geniteur de cette courbe, lors que le point qui la trace estoit en E, ait eu la position GED, touchant le cercle BL en D. Et ayant joint ED, soit EG perpendiculaire à elle, qui touchera l'Epicycloide BEK au point E, par notre propos.... du traitè de l'Evolution des lignes courbes, car il est aisè de la rendre generale⁴⁾.

Il faut donc seulement demonstrer que EG estant prolongée rencontre l'Epicycloide KFN à angles droits. car il s'en suit de la que cette courbe se descrit par l'evolution de la courbe BEK, par notre prop.... de l'Evolution des courbes⁵⁾. Il est certain que EG rencontre la circonference KC au point de contact du cercle ED, parce que DEG est un demicercle à cause de l'angle droit DEG.

4) Voir la Prop. XV de la Pars Secunda de l'‘Hor. osc.’ ou bien la partie A de notre Appendice à la Pars Secunda. La proposition doit en effet être généralisée, car dans la lettre de Descartes à Mersenne citée dans la note 1 de la p. 388, ainsi que dans le Commentaire de van Schooten (même endroit) et dans la Prop. XV de Huygens il n'est question que d'une courbe roulant sur une droite. Ici Huygens admet que la droite qui relie le point considéré de la figure roulante au centre instantané de rotation est également normale à la courbe décrite par ce point, lorsque la figure roule sur une courbe. Descartes (quoiqu'il dise pouvoir démontrer la proposition dans le cas considéré par lui ‘d'une autre façon, plus belle a mon gré & plus Geometrique’) se contente d'en faire voir la vérité en assimilant la courbe roulante à ‘nn polygone qui a une infinité de costez’. Or, cette même considération peut servir à établir le théorème lorsque la figure roule sur une courbe: il suffit d'assimiler cette dernière à un polygone, dont les côtés correspondent exactement à ceux de la figure roulante qui viennent s'y appliquer. C'est la probablement la voie suivie par de Vaumesle qui dit (T. VIII, p. 117) avoir ‘trouvé la tangente de la cijcloïde circulaire par la methode de mr. des Cartes’, puisqu'il ajoute ‘Jay reconnu que les tangentes de lvne et de lautre cycloïde se trouvent de mesme maniere’: il connaissait (T. VIII, p. 127) ‘la geometrie de mr. des cartes commentéé par Scoothen’ et considère (même endroit) fort ingénieusement des polygones réguliers roulant l'un sur l'autre. C'est à ce sujet que se rapporte la petite figure de Huygens de la p. 108 du Manuscrit E que nous insérons ici [Fig. 141]. Il ne paraît pas que Huygens se soit appliqué à généraliser la démonstration plus rigoureuse de la Prop. XV de la Pars Secunda. Comparez la note 9 de la p. 403 qui suit.

5) Il s'agit de la Prop. IV de la Pars Tertia de l'‘Hor. osc.’

[p. 402]

Soit VG le cercle generateur de l'Epicycloide KFN, et qu'il touche aussi le cercle KC en G: Et que EG prolongée couppe la circonference GV en H. Puis donc que l'arc BDL est egal à la demie circonference DEG; et que l'arc DB est egal à l'arc DE, par la nature de la courbe BEK; l'arc DL sera aussi egal a l'arc EG. Mais l'arc EG est a l'arc GH comme le diametre DG a GV, c'est à dire comme AD a AG, (parce que AD, AG, AV sont proportionelles) ou comme l'arc DL à l'arc GK. Donc les arcs EG, DL estant egaux, les arcs GH, GK seront egaux de mesme. d'ou s'ensuit que le point H est le point traçant de l'Epicycloide KFN, lors que son cercle generateur est en GV. Et par la propos. susdite du Traitè de l'Evolution⁶⁾, il paroit que GH, qui est la continuation de la droite EG, rencontre la courbe KFN en ce point H à angles droits, ce qui restoit à demonstrer.

6) C.à.d. par la Pɹop. XV de la Pars Secunda, supposée généralisée (note 4).

Propos. 2.

La courbe d'une Epicycloide est au diametre de son cercle generateur comme deux fois la somme des diametres du cercle generateur et du cercle immobile qui sert de base, au rayon du mesme cercle immobile.

Il est evident que l'evolution de la demie Epicycloide BEK se terminant en N, comme il a estè dit, la droite BN est egale a la courbe BEK. et parce que AN, AC, AB sont proportionelles il s'en suit que NC est a CB, comme CA à AB ou AO⁷⁾. Et en composant, NB à BC, c'est a dire la demie Epicycloide au diametre de son cercle generateur comme CO a OA, Et l'Epicycloide entiere BKP à BC, comme deux fois CO à OA; ce qu'il fallait demonstrer.

7) Cette dernière équation est d'ailleurs équivalente à l'hypothèse initiale: ‘le cercle KM estant supposè estre au cercle KC comme le cercle CB au cercle BL’.

[p. 403]

Il est à noter que ces Epicycloides sont des lignes geometriques quand les diametres des cercles generateur et immobile sont commensurables⁸⁾.

8) Dans le Livre Second de sa Géométrie Descartes parle comme suit: ‘Pour comprendre ensemble toutes celles [c.à.d. toutes les courbes planes] qui sont en la nature, et les distinguer par ordre en certains genres, je ne sache rien de meilleur que de dire que tous les points de celles qu'on peut nommer géometriques, c'est à dire qui tombent sous quelque mesure précise et exacte, ont nécessairement quelque rapport à tous les points d'une ligne droite, qui peut être exprimée par quelque équation, en tous par une même’.
Or, l'épicycloïde extérieure s'exprime en coördonnées rectangulaires par les équations où R et r désignent les rayons du cercle immobile et mobile; lorsque n est commensurable, le paramètre φ peut être éliminé. La cycloïde au contraire n'est pas ‘géométrique’.

§ 3.

Spatium epicycloide et basi sua comprehensum, est ad circulum genitorem Epicycloidis, ut tripla semidiametrus circuli baseos cum diametro circuli genitoris ad radium circuli baseos⁹⁾.

9) De Vaumesle avait trouvé, par la considération de polygones réguliers et égaux roulant l'un sur l'autre, que la surface de la cardioïde, y compris le cercle générateur, est le double de celle de la cycloïde ordinaire engendrée par un cercle de même grandeur (T. VIII, p. 117); en d'autres termes que la surface de la cardioïde sans le cercle générateur, est le quintuple de ce dernier (même endroit et p. 127). C'est ce résultat - c'est à la méthode de de Vaumesle que se rapportent les figures (Fîg. 141 bis) de Huygens de la p. 174 du Manuscrit E - que Huygens généralise en suivant une méthode différente.

[p. 404]

[Fig. 142.]

Dans la mesme figure [Fig. 142] soit pris un autre point Q dans l'Epicycloide BQK, pres du point E, et soit QP sa tangente, qui rencontrera donc l'Epicycloide KHN à angles droits, comme en P; Et coupera necessairement la circonférence CK; prenons que ce soit en R. Or les points de contact E Q peuvent estre infiniment pres l'un de l'autre et aussi les points d'intersection G R; la raison de HE a GE et de PQ a QR demeurant tousjours les mesmes que de VD a DG. Partant HQP, GQR peuvent estre considerez comme des triangles des quels la proportion est la mesme que du qu. HE au qu. EG, ou du qu. VD au qu. DG¹⁾. Donc tout l'espace BEKN à l'espace BEKC aura la raison du qu. VD au qu. DG, parce qu'en concevant de tangentes infinies²⁾ le long de la courbe BQK, elles diviseront tout l'espace KPNBQK en une infinitè de triangles tels que PQH, qui auront chacun à leur partie RQG la mesme raison que le qu. HE au qu. EG, ou que le qu. VD au qu. DG. Donc aussi dividendo, l'espace KHNC sera à BEKC comme l'exces du qu. VD sur le qu. DG est au qu. DG. Mais l'espace BEKL est à KHNC comme le qu. DG au qu. GV. donc ex aequo³⁾ in propositione perturbata, l'espace BEKL sera à BEKC, comme le qu. VD - qu. DG au qu. GV, c'est a dire comme le rectangle de VG + 2GD et VG, au qu. VG, ou comme VG + 2DG à VG. Et l'espace BEKL à BLKC comme VG + 2DG a 2VG + 2DG. ou comme AK + 2AL à 2AK + 2AL. Sed BLKC est ad semicirc. BRC comme 2BL + 2CK à BL: Parce que BLCK est egal au ▭ ½BL + ½CK et BC. Et le demicercle BRC egal au ▭ ¼BL et BC. Et partant en ostant la commune hauteur BC et quadruplant, sera BLKC au demicercle BRC comme 2BL + 2CK à

1) Ou plutôt: ‘Partant HQP, GQR, lesquels peuvent être considérés comme des triangles dont la proportion est égale à HE² : EG², sont aussi entre eux comme VD² : DG².’

2) C.à.d. une infinité de tangentes.

3) Comparez la p. 396 du T. XVI.

[p. 405]

BL, ou comme 2AK + 2AL à AL. Mais l'espace BEKL estoit à BLKC comme AK + 2AL à 2AK + 2AL, donc ex aequo BEKL au demicercle BRC comme AK + 2AL à AL. C'est a dire comme 3AL + LK a AL.

§ 4.

[Voir la p. 406 du T. XIV (p. 166 du Manuscrit E). Le calcul se rapportant à la cycloïde, découpée de la même manière que l'épicycloïde, est une suite du calcul des §§ précédents. La page 166 du Manuscrit date sans doute également de 1678, non pas de 1679, puisque les pages suivantes se rapportent encore en partie au même sujet: voir la Fig. 141 bis et aussi la Fig. 141 aux p. 402-403 qui précèdent].