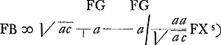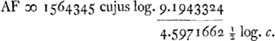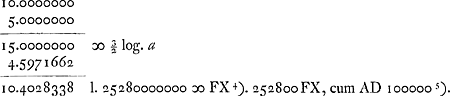Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695

[p. 374]

Appendice II
À la pars prima de l'‘Horologium oscillatorium’.
[1659-1693 ou 1694]

[Fig. 121.]

A.¹⁾

Quaeritur tempus per quadrantem Circumferentiae circuli, quod dubito an inveniri possit.

Ut AT ad GF [Fig. 121] ita faciendum YZ ad aliam quae erit tempus per KH, sed ut AT ad GF ita IN ad NL²⁾.

Ratio temporis per KH ex EG ad tempus per QR cum motu aequabili dimidio ex DA³⁾ componitur ex rationibus KH ad QR et ½ AP ad MN⁴⁾, hoc est ex DG sive LN ad NG et ½ AP ad MN, hoc est eam quam ½ qu. AP ad ▭ MNG.

⁵⁾

1) Chartae Mechanicae f. 73 verso, datant de décembre 1659. Consultez sur la f. 73 recto et verso les notes 1 et 4 des p. 392-393 du T. XVI. Nous n'avons pas reproduit en cet endroit le calcul de la p. 73 v. disant que Huygens ne trouva que plus tard une solution approchée pour le ‘tempus per quadrantem circumferentiae’. Ce n'est en effet que dans l'‘Hor. osc.’ qu'on trouve la valeur numérique approchée 34:29 (inférieure à la vraie valeur) du rapport de la période d'une oscillation de 180^o du pendule simple à la période de l'oscillation extrêmement petite du même pendule (voir la note 2 de la p. 101 qui précède). Evidemment ce rapport ne pouvait être déterminé avant que, dans ce même mois de décembre, la règle qui donne la formule de la période de l'oscillation extrêmement petite avait été trouvée (T. XVI, p. 410). Pour trouver ensuite le rapport 34:29 Huygens peut s'être servi (voir la note 2 de la p. 378) de l'équation de la f. 73 v. Il est intéressant de savoir que cette formule qu'on retrouve dans la Pièce C de 1669 qui suit, a déjà été trouvée par lui en 1659 au début de ses recherches sur ce sujet.

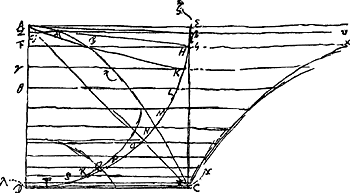
2) Nous conservons ce début quoique Huygens n'ait pas poursuivi ce calcul. Dans la proportion AT : GF = YZ: tempus per KH, il est évident que par ‘YZ’ il faut entendre ‘tempus per YZ’. La très petite droite KH est sans doute supposée parcourue avec la vitesse provenant d'une chute de E en G. Or, de quelle hauteur au-dessus de T Huygens suppose-t-il tombé le point pesant qui parcourt la petite droite YZ? En partant de la proportion du texte on constate, en faisant le calcul, que, pour toute position de T, le point de départ est situé à une hauteur ¼ AD ou ¼ a au-dessus de lui. En d'autres termes: la demi-circonférence DTA est parcourue avec la vitesse constante ½ ag (où g est l'accélération de la pesanteur), c.à.d. avec la moitié de la vitesse qui proviendrait d'une chute suivant DA.
La proportion AT : GF = IN : NL sert à introduire ensuite la grandeur constante NL ou a au lieu de la variable AT pour toute position du point G. La considération de la figure conduit à la relation , où x = DN. Pour que , il faut que les points I soient situés sur la parabole de la figure, qui passe par le point E et dont la distance du sommet au point D est égale à a.
On a maintenant: tempus per KH = a. YZ/IN (où YZ désigne toujours le ‘tempus per YZ’), où le numérateur est constant lorsque tous les ‘arcs’ YZ qui ‘composent’ la demi-circonférence DTA sont pris égaux entre eux. Pour trouver le temps qui correspond à la chute le long de EA il faudrait intégrer l'expression trouvée pour toutes les valeurs de IN de a à a √2. Ce qui rend cette intégration, même approchée, difficile ou impossible, c'est que les éléments YZ ne se trouvent pas sur une droite mais sur une circonférence.
Observons que la demi-circonférence DTA réapparaît dans les démonstrations des propositions se rapportant à la chute cycloïdale; voir les p. 406 et suiv. du T. XVI et les figures de la Pars Secunda de l'‘Hor. osc.’.

3) De nouveau Huygens compare le mouvement accéléré suivant le quart de circonférence EKA avec un mouvement uniforme, mais cette fois il a soin de prendre ce dernier suivant une droite. Comparez sur le résultat du calcul la pièce C qui suit (note 1 de la p. 378).

4) La ligne DMP est la parabole qui donne les vitesses. Comparez la Fig. 7 de la p. 398 du T. XVI. La vitesse constante le long de QR est à la vitesse accélérée en G comme ½ AP : MN.

5) Le temps nécessaire pour parcourir un élément QR, qui est constant lorsque tous les élements QR sont égaux entr'eux, étant représenté par la grandeur constante, d'ailleurs arbitrairement choisie, a, le temps nécessaire pour parcourir l'élément KH correspondant à QR aura la valeur y du texte.

[p. 376]

B.¹⁾

De descensu accelerato gravium. Hypotheses. De composito motu. Theorema Galilei exactè demonstratum. Aliud de ascensu. De aequali ascensu et descensu. Eadem super planis contingere &c. quae de descensu super planis, et curvis superficiebus, et de curva Cycloide. De motu pendulorum. Circularem non esse isochronum contra Galilei et multorum opinionem, difficilem esse determinationem temporis per quadrantem circuli et arcus minores. quaenam sit proxima. Quaenam ex motu per superficies applicentur motui penduli circularis. Pendulum Cycloidicum. Proprietas evolutionis ad Theoremata de Evolutione et dimensione curvarum remittitur.

1) La Pièce B est empruntée à la p. 224 du Manuscrit D datant de septembre 1669 (la p. 225 porte la date du 29 septembre). En ce mois Huygens s'apprêtait donc à rédiger définitivement les théorèmes de la Pars Secunda sur le mouvement des corps tombants dont il s'était occupé aussi en 1659 (p. 125-141 du T. XVII). Les p. 222-223 du Manuscrit D contiennent des projets de rédaction de quelques théorèmes sur la chute que nous ne reproduisons pas. Nous plaçons la pièce B dans un Appendice à la Pars Prima, parce qu'il y est e.a. question de la détermination du ‘tempus par quadrantem circuli’, comme dans les Pièces A, C, D et E.

C.²⁾

De tempore descensus per arcum quadrantis circumferentiae.

[Fig. 122.]

AC [Fig. 122] parabola.

PR, PS, PT proportionales.

Item PY ad PS ut PT ad PV. Erit tempus per quadrantem BD ad tempus accelerati motus per AD³⁾ ut spatium infinitè extensum AVVVDA ad spatium infinite extensum ATTCDA, hoc est ad duplum quadratum ABCD.

2) La Pièce C est empruntée à la p. 68 v. du Manuscrit G, datant d'un des trois premiers mois de 1691.

3) Contrairement à ce qu'il avait fait en 1659 (p. 375, note 3). Huygens compare ici (voir la suite du texte) les temps nécessaires pour parcourir les éléments du quart de circonférence BD avec les temps dans lesquels les éléments correspondants de la droite verticale AD sont parcourus d'un mouvement accéléré par un point qui tombe de A. Il est évident que la formule qui donne le rapport du temps suivant BD au temps suivant AD devient néanmoins la même.

[p. 377]

Si enim DC referat celeritatem qua infima PP percurritur, referet MR celeritatem qua percurritur MI.

Tempus autem per infimum PP ad tempus per IM ut MR ad DC, nempe in ratione contraria celeritatum. Ergo tempora ut DC seu MS ad MT. Hinc singulae TP ad se invicem ut tempora motus accelerati ex A per singulas lineas PP istis spatijs respondentes. Tempora autem per singulos arcus YY sunt ad tempora illa per sibi respondentes PP ut ipsae singulae YY ad singulas PP longitudine, hoc est ut singulae respondentes SP ad YP ut facile ostenditur; hoc est ut singulae respondentes VP ad TP. Hinc per propos. 2. Archimedis de Conoidibus et Sphaeroidibus⁴⁾ erunt omnia simul tempora per lineas PP, hoc est tempus motus accelerati per AD ad tempora omnia per arcus YY, hoc est ad tempus per arcum BD ut omnes TP ad omnes VP. hoc est⁵⁾ ut spatium infinitum AVVDA ad spatium infinitum ATTCDA, seu 2 quadratum ABCD⁶⁾).

4) Voir la note 1 de la p. 179 qui précède.

5) Huygens considère ici le rapport inverse, savoir celui du ‘tempus per arcum BD’ à celui du ‘tempus motus accelerati per AD’.

6) La courbe CTTT est une hyperboloïde. Son équation y¹x^½ = a^3/2 permet de déterminer, d'après la méthode de Huygens de 1657 (note 8 de la p. 289 du T. XIV) le rapport de l'aire ABCD à l'aire BTTC. Puisque p (note nommée) a ici la valeur 1 et q la valeur ½, ou a , c.à.d. les deux aires sont égales, en d'autres termes: le ‘spatium infinitum [c.à.d. l'espace s'étendant jusqu'à l'infini] ATTCDA’ est égal au double du carré ABCD.

[p. 378]

Oporteret hujus curvae quadraturam dari¹⁾.

Stanni folium specularis incidatur et pondus comparetur²⁾.

1) Le résultat du calcul est donc (lorsqu'on introduit le symbole de Leibniz ∫):
tempus per arcum BD [Fig. 122]: tempus motus accelerati per AD En 1659 (Pièce A) Huygens avait trouvé (sans toutefois se servir du symbole Σ d'Euler):
tempus per arcum ou Comme le temps nécessaire pour parcourir du mouvement uniforme considéré l'élément QR de la Fig. 121 était réprésenté par a (p. 375, note 5), le temps nécessaire pour parcourir la droite entière DA était a²/QR. Ce temps est égal, d'après l'hypothèse faite pour la grandeur de la vitesse constante, à celui de la chute accélérée suivant DA. On a donc: tempus per arcum BD: tempus motus accelerati per AD ce qui s'accorde avec le résultat du calcul de 1691 (début de la présente note).

2) Est-ce pas un pesage de ce genre que Huygens avait trouvé entre 1659 et 1673 la valeur approchée 34:29 (note 2 de la p. 101) du rapport en question? Nous ne le pensons pas, puisqu'il propose ici une méthode pratique qui ne pouvait pas servir pour obtenir, comme il le dit dans l'‘Hor. osc.’, une valeur du rapport ‘aussi proche qu'on voudra’. Il s'agissait donc probablement avant 1673 d'un calcul approché de la surface représentée par l'intégrale de la note 1, à moins que Huygens n'ait suivi déjà en ce temps la méthode de la Pièce E qui suit ou une autre méthode que nous ne connaissons pas. Voir encore la note 2 de la p. 384 qui suit.

D.³⁾

Ad computanda tempora descensus per arcus circumferentiae⁴⁾.

[Fig. 123.]

3) Manuscrit I, p. 100 et suiv. De ces deux pages la première date de 1693 ou 1694 suivant la place qu'elle occupe dans le Manuscrit. L'autre est le recto d'un feuillet collé dans le livre. La division en §§ est de nous.

4) En marge: ‘Vide lib. G. pag. 34. 1’. C'est la page, numérotée par Huygens, que nous avons désignée par 68 verso (p. 376, note 2).

[p. 379]

§ 1. AF ∞ c [Fig. 123].

AD ∞ a ∞ latus rectum parabolae ABC.

FB, FG, FX proportionales.

⁵⁾

cujus igitur logarithmus est 2 log. a - ½ log. a - ½ log. c sive 3/2 log. a - ½ log. c. 3/2 l. a - ½ l. c ∞ l. temporis per EG⁶⁾, celeritate ex AF; sive rectae FX.

ζβ est ∞ ¼ arcus EH⁷⁾

Zδ. Zβ. ZV proportionales⁸⁾.

Erit ZV pauxillo brevior tempore per EH quia esset aequalis tempori per rectam perpendicularem aequalem EH arcui seu per quadruplam Eβ. sed potest sumi tanquam aequalis⁹⁾.

5) FX correspond donc à PT (ou MT) de la Fig. 122 de la Pièce C; x de la Fig. 122 s'appelle maintenant c.

6) En disant que la droite FX représente le ‘tempus per EG’ Huygens considère cette droite comme une partie d'une surface. C'est en effet la bande découpée par deux horizontales de la surface XCDAX (Fig. 123, laquelle s'étend jusqu'à l'infini vers le côté droit), qui représente le temps d'une chute verticale suivant la largeur de cette bande. À droite la bande est limitée par une partie de la courbe CX et dans le cas du ‘tempus per EG’, où EG est le premier élément de la verticale, la bande s'étend jusqu'à l'infini. Dans la Pièce C Huygens disait que la surface considérée est proportionnelle au temps. Ici il l'égale au temps. Un peu plus loin, il dit de même que le temps du mouvement accéléré suivant AD est égal au double du carré AC. Il est évidemment plus correct de dire que la droite FX représente non pas un temps mais l'inverse d'une vitesse.

7) L'élément ζβ (où le point ζ est identique avec le point E) est un élément de la verticale dont la longueur est égale par hypothèse à ¼ de l'arc EH.

8) Dans la Fig. 123 V est donc situé sur la courbe CX.

9) Huygens se propose apparemment de chercher une valeur approchée du temps nécessaire pour parcourir le quart de circonférence ED du mouvement accéléré tel qu'il a lieu en réalité; à cet effet il divise le quart de circonférence en 12 arcs égaux et suppose chacun d'eux parcouru avec une vitesse constante. La droite verticale égale à l'arc EH dont il est question dans la note 7 est parcourue dans un même temps, soit qu'on considère le mouvement accéléré naturel, soit qu'on suppose cette droite verticale parcourue avec la vitesse constante qui résulte de la chute verticale le long de Eβ = ¼ EH. C'est ce temps-là que Huygens désigne par ‘ZV’ quoiqu'en réalité (comparez la note 6) il soit égal à l'aire de la bande limitée par les horizontales AE (de longueur infinie) et ZV. Le ‘tempus per EH’, c.à.d. le temps dans lequel l'arc EH est parcouru dans le mouvement réel, est évidemment, comme le dit le texte, tant soit peu plus long que le temps nécessaire pour parcourir la verticale égale à EH.

[p. 380]

Porro incipiendo ab FX et finiendo in DC, summa applicatarum est minor tempore per quadrantem ED. si nempe ducatur in EH arcum¹⁾.

Sed incipiendo ab ZV et finiendo in λY summa applicatarum erit major tempore per eundem quadrantem ED. ducta nempe in arcum EH²⁾.

AF, Aγ, Aθ &c. sunt sinus angulorum EAH, EAK &c.

Tempus motus accelerati per AD erit ∞ 2 quad. AC.

Ratio horum est, quia si arcus EH ponatur peractus aequabili celeritate quanta ex altitudine EG, vel per EH, acquirit, quam refert FB applicata in parabola AC, sumetur tempus vero brevius. Item si pro tempore descensus continuati per HK sumatur illud quo HK percurreretur celeritate aequabili quanta ex EK, quam refert γϰ, rursus sumitur tempus vero brevius.

quia autem arcus aequales ponuntur, erunt tempora quibus percurri ponuntur in ratione contraria celeritatum, hoc est ut applicatae in curva CX, ad rectam AD.

§ 2. Ponatur primo quadrantis arcus ED divisus in 10 partes aequales³⁾.

Ergo AF ∞ sin 9. gr.

1) On obtient une limite inférieure pour le temps de la chute le long de HD en supposant chacun des 12 arcs égaux, dans lesquels HD est divisé, parcouru avec la vitesse finale telle qu'elle est en réalité pour cet arc. Pour chaque arc le temps est alors égal au produit de EH par l'‘applicata’, c.à.d. par l'horizontale se terminant à la courbe CX qui passe par le point le plus bas de l'arc considéré. La limite inférieure totale est donc égale au produit de EH par la somme des horizontales de FX à DC.

2) On obtient une limite supérieure pour le temps correspondant aux 11 derniers arcs en les supposant parcourus avec la vitesse initiale. Il faut encore y ajouter le temps du premier arc. La suite du texte donne d'ailleurs l'explication exposée dans les notes 1 et 2.
Il est vrai que pour le premier arc la valeur trouvée était inférieure au vrai temps, de sorte que, lorsqu'on ajoute cette valeur à la limite supérieure obtenue pour les 11 arcs suivants, il n'est pas rigoureusement démontré qu'on obtient encore une limite supérieure du temps nécessaire pour parcourir le quart de circonférence. Mais Huygens avait dit que la valeur trouvée pour le premier arc diffère sans doute très peu de la vraie valeur.

3) Le § 2 a peu d'importance puisque Huygens retourne au §3 à la division du quart de circonférence en 12 parties, conformément à la Fig. 123.

[p. 381]

⁴⁾⁵⁾

§ 3. Sit arcus quadrantis ED divisus in 12 partes aequales.

⁶⁾⁷⁾

4) D'après la formule 3/2 log. a - ½ log. c = log. temporis .... du § 1.

5) Quoique le rayon ait la longueur 10⁵, le calcul de FX (note 4) a eu lieu comme si la longueur du rayon était 10¹⁰.

6) La remarque de la note précédente s'applique aussi au calcul de AF et des horizontales suivantes. Mais dans la valeur finale obtenue pour chacune de ces lignes Huygens omet à bon droit les 5 zéros qu'il avait écrit dans la valeur de FX du § 2.

7) Le nombre est plus près de 10.1505150 que de 10.1505140, mais Huygens prend cette dernière valeur puisqu'il s'agit de trouver une ‘summa minor’. Une remarque analoque s'applique à plusieurs autres nombres. Une somme plus exacte ne peut évidemment être obtenue que lorsqu'on tire de la table des logarithmes une valeur plus exacte pour chaque nombre séparément.

[p. 382]

^1)2)3)4)

1) D'après ce qui a été dit à la p. 379 (note 7) il faut, pour calculer ZV (inverse d'une vitesse), prendre la longueur c égale à ¼ de l'arc EH lui-même. Il n'est donc pas évident pourquoi Huygens prend le nombre 13052 au lieu de 13095. Apparemment il prend ¼ de la projection de l'arc EH sur la verticale, c.à.d. du sinus de 7^o30′, ce qui fait d'ailleurs bien peu de différence. Les mots ‘sit 3263’ indiquent qu'il ne s'agit pas d'une erreur, mais qu'il croyait pouvoir se contenter de cette valeur de ZV. Comme on voit, il n'a calculé qu'ensuite (en prenant π = 22/7) la longueur 13095 de l'arc EH.

2) C'est le produit de la ‘summa minor’ par la longueur de ‘1/12 quadrantis’. C'est donc (note 1 de la p. 380) la limite inférieure cherchée du temps d'une chute le long du quart de circonférence, le temps de la chute le long de la verticale étant représenté (note 6 de la p. 379) par 2.10¹⁰. Mais ce dernier temps est à celui d'une demi-oscillation simple le long d'un très petit arc dans le rapport √2: ½ π (comme Huygens le dit dans la Pièce E). Le rapport cherché est donc 21597583500 : 2.10¹⁰ × 2 : 2.22145 ou 2.15976 : 2.22145 = 0.97. En d'autres termes: cette limite inférieure n'est d'aucun usage puisqu'elle est même inférieure à l'unité. Avant 1673 Huygens avait trouvé la limite inférieure 34:29 ou 1.1724 beaucoup plus approchée (note 2 de la p. 378).

3) s. = subtrahendo.

4) Pour passer de la ‘summa minor’ à la ‘summa major’ (note 2 de la p. 380) il faut retrancher de la première la droite CD et y ajouter la droite ZV. C'est par erreur que Huygens retranche aussi la droite FX qui dans la ‘summa major’ correspond au temps du deuxième arc d'en haut. Il aurait donc dû trouver pour la ‘summa major’ 2090700, et par conséquent (note 2) pour la limite supérieure du rapport cherché . (Le nombre erroné de Huygens donne pour cette limite du rapport la valeur 2.23753 : 2.22145 = 1.007 inférieure à la vraie valeur).

[p. 383]

E.⁵⁾

ratio temporis per radium ad tempus oscillationis minimae, eadem quae lateris quadrati in circulo ad arcum quadrantis.

2623 ⫟ 2222 ratio minor quam temporis per quadrantem circumferentiae ad tempus oscillationis minimae. Sed antehac experienti videbatur mihi esse proxime quae 12 ad 11, non 13 ad 11 ut hic.

5) La Pièce E fait suite à la Pièce D. Elle occupe le verso du feuillet mentionné dans la note 3 de la p. 379.
Le calcul de la Pièce D ne pouvant apparemment conduire à des limites convenables à moins que la subdivision du quart de circonférence ne fût poussée beaucoup plus loin - nous trouvons en effet, que pour atteindre la limite inférieure 1.1724 d'avant 1673 (note 2) il ne suffit mème pas de diviser le quart de circonférence en mille arcs égaux - Huygens chercha une autre méthode, tout en conservant la division du quart de circonférence en douze parties seulement. Il n'explique point cette méthode. La colonne des nombres qu'il additionne donne une ‘summa minor’ (20031) beaucoup plus grande que la ‘summa minor’ (16493) de la Pièce D, et la valeur 2623:2222 ou 1.18047 qui en résulte pour la limite inférieure du rapport cherché ne s'écarte pas notablement de la vraie valeur. La méthode fait donc l'effet d'être bonne. Le premier nombre de la colonne, 2768, correspondant à 276800 (FX) de la Pièce D - on trouve son logarithme au début du § 3 - peut évidemment être déterminé plus exactement - il deviendra un peu plus petit - et il serait sans doute également possible de déterminer exactement les autres nombres de la colonne si nous savions comment, d'après Huygens, il faut les calculer. Le nombre 13095 doit être remplacé par 13090 puisque Huygens l'à calculé en prenant π = 22/7. On trouvera donc par cette méthode une valeur qui s'écarte quelque peu de 1.18047 et peut constituer une limite inférieure se rapprochant beaucoup de la vraie valeur 1.18033 (voir la fin de la présente note). En laissant aux nombres de la colonne leurs valeurs, mais en remplacant 13095 par 13090 et 2222 par 2221, 45 on trouve (par hasard?) pour la limite du rapport précisément 1.18033.
Quelle peut avoir été la méthode suivie? On peut représenter graphiquement par des aires les 12 quantités qu'il s'agit de sommer en écartant la première horizontale ainsi que les horizontales FX.... DC de la Fig. 123 l'une de l'autre à des distances égales entre elles (savoir des distances de 1/12 quadrantis). Pour trouver une forme de plus en plus exacte de la courbe déformée XC il faudrait pousser la subdivision plus loin et prendre toujours des distances égales entre chaque paire d'horizontales correspondant aux extrémités d'arcs égaux dans la Fig. 123. La courbe XC restera partout concave, puisque plus la partie considérée de la courbe est petite, plus aussi la déformation est uniforme.
Dès lors il est facile de trouver une limite supérieure pour les 11 dernières quantités: il suffit de remplacer la courbe XC déformée par une droite brisée, de sorte que toutes les horizontales conservent leurs longueurs et que chacune des 11 quantités est représentée par un trapèze. On trouve ainsi, en partant des valeurs de la Pièce D, les 11 quantités

2367	presque toutes supérieures aux quantités correspondantes de Huygens (les trois derni-
1791	ères seulement sont inférieures) et dont la somme 14609 n'est pas beaucoup plus
1514½	grande que la somme correspondante, 14495, de ses quantités à lui. Pour obtenir la
1347½	somme 14609 il suffit d'ailleurs de prendre le nombre 12725 de la colonne de la
1235½	Pièce D et d'y ajouter ½ (2768 + 1000) ou 1884.
1156	Pour trouver une limite inférieure pour les 11 dernières quantités on pourrait
1098½	limiter chaque trapèze nou pas par une corde de la courbe FX déformée, mais par
1057	une tangente à cette courbe, de sorte que l'une des horizontales qui limitent le
1029	‘trapèze’ est quelque peu raccourcie (ou bien que les deux horizontales soient rac-
1011	courcies, si le point de contact choisi ne se trouve pas sur une d'elles, mais entre
1002	elles). Ce n'est pas là cependant la voie suivie par Huygens puisque de cette façon les rrois dernières quantités trouvées par lui devraient, comme les autres, être inférieures à celles que nous venons de calculer.

Quant à la première quantité Huygens prend apparemment pour une limite du temps cherché le double du produit de FX par 1/12 quadrantis (ce qui explique peut-être l'erreur signalée dans la note 4; il est possible qu'en ce moment il était déjà d'avis qu'on peut prendre le double de FX dans la ‘summa minor’; or, s'il avait réellemeut pris le double, il eût fallu retrancher FX, comme il le fait, dans le calcul de la ‘summa major’). En effet, la bande supérieure de la figure déformée dont il est question un peu plus haut s'étend jusqu'à l'infini (comme celle de la figure non déformée) et a donc une aire beaucoup supérieure à celle du rectangle formé par FX et la droite verticale égale à 1/12 quadrantis. Pour démontrer que la valeur prise par Huygens est bonne, il faudrait faire voir (comparez la Fig. 121 de la Pièce A): où b = a sin 7^o30′ est la projection du premier 1/12 quadrantis sur la verticale. Ou plus brièvement Le développement en serie de l'intégrale donne Il faudrait donc faire voir que ou ou 0.26106 + 0.00045 .... > 0.26180, ce qui pourtant n'est pas vrai.
Mais on voit que la valeur prise par Huygens, tout en étant quelque peu supérieure à la vraie valeur, en est très rapprochée. Il est donc possible, quoique sa méthode nous soit inconnue, que l'ensemble de toutes les quantités qu'il considère constitue en effet une limite inférieure.
Ajoutons qu'en prenant le double du produit FX par 1/12 quadrantis comme premier nombre de la ‘summa major’, telle que nous l'avons considérée, celle-ci devient , ce qui donne pour la limite supérieure du rapport cherché . Quant à la vraie valeur de ce rapport, elle est, d'après la note 1 de la p. 378, ¹⁾ ou, en posant : ou Or, on a é s'écrit donc

1 + 1²/2² × 1/2 + 1²×3²/2²×4²×1/4 + 1²×3²×5²/2²×4²×6²×1/8 +
Il est quelque peu inférieur à 1.18033²⁾.

1) Ou, si l'on veut,

2) On peut consulter sur ce calcul L. Euler ‘De Motu oscillatorio penduli cuiuscunque, dum arcus datae amplitudinis absolvit’, Act. Ac. Scient. Imp. Petrop. pro Anno MDCCLXXVII, Pars Posterior, Petropoli, Typ. Ac. Scient. MDCCLXXX, p. 159-182. Euler considère plus généralement le cas où l'amplitude d'une vibration simple est 2ζ; le rapport de la période d'une oscillation à celle d'une oscillation fort petite s'écrit alors

1 + 12/22× c2 + 12×32/22×42 c4 + 12×32×52/22×42×62 c6 + ..., où c = sin. ½ ζ.

Cette série a d'ailleurs déjà été trouvée sous une forme peu différente de celle d'Euler par P.P. Elvius - qui s'in spire de la méthode de Newton, exposée dans le ‘Tractatus de Quadratura Curvarum’ de 1704, pour développer l'intégrale trouvée par lui-même indépendamment de Huygens dont il ne connaît que les ouvrages imprimés - et publiée par lui dans son travail ‘Theorema de oscillationibus pendulorum in arcubus circularibus’ (Acta Literaria et Scientiarum Sueciae, Anni MDCCXXXIV, Upsaliae, Sumtibus Reg. Soc. Lit. & Scient.), après que G. Vallerius eut publié dans les Acta de 1731 son article ‘Observatio & Experimentum de Funependulorum Vibrationibus’. Vallerius trouve e.a. pour le rapport de la période d'une oscillation de 180o à une oscillation de 20o, 225:189 ou 1,191 .., donc une valeur trop grande mais fort proche de la valeur véritable.

1) Ou, si l'on veut,

2) On peut consulter sur ce calcul L. Euler ‘De Motu oscillatorio penduli cuiuscunque, dum arcus datae amplitudinis absolvit’, Act. Ac. Scient. Imp. Petrop. pro Anno MDCCLXXVII, Pars Posterior, Petropoli, Typ. Ac. Scient. MDCCLXXX, p. 159-182. Euler considère plus généralement le cas où l'amplitude d'une vibration simple est 2ζ; le rapport de la période d'une oscillation à celle d'une oscillation fort petite s'écrit alors

1 + 12/22× c2 + 12×32/22×42 c4 + 12×32×52/22×42×62 c6 + ..., où c = sin. ½ ζ.

Cette série a d'ailleurs déjà été trouvée sous une forme peu différente de celle d'Euler par P.P. Elvius - qui s'in spire de la méthode de Newton, exposée dans le ‘Tractatus de Quadratura Curvarum’ de 1704, pour développer l'intégrale trouvée par lui-même indépendamment de Huygens dont il ne connaît que les ouvrages imprimés - et publiée par lui dans son travail ‘Theorema de oscillationibus pendulorum in arcubus circularibus’ (Acta Literaria et Scientiarum Sueciae, Anni MDCCXXXIV, Upsaliae, Sumtibus Reg. Soc. Lit. & Scient.), après que G. Vallerius eut publié dans les Acta de 1731 son article ‘Observatio & Experimentum de Funependulorum Vibrationibus’. Vallerius trouve e.a. pour le rapport de la période d'une oscillation de 180o à une oscillation de 20o, 225:189 ou 1,191 .., donc une valeur trop grande mais fort proche de la valeur véritable.