Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695

[p. 369]

Appendice I
À la pars prima de l'‘Horologium oscillatorium’.
[1668-1669.]

A. Ad inveniendas longitudines in mari, ex duabus aequalibus solis altitudinibus et hora pendulorum¹⁾.

[Fig. 119.]

PLQ meridianus. P polus. Z. zenit, EQ aequator. A1 parallela horizontis. LD ecliptica.

1 locus solis in ecliptica cum ante meridiem observaretur ejus distantia a vertice Z1²⁾.

2 locus solis in ecliptica cum post meridiem observatus fuit in eadem distantia a vertice atque ante meridiem. translato nempe puncto eclipticae 2 in A, et 1 in B.

Intercessere autem inter observationem utramque horae horologij 10. daturque punctum eclipticae 1 puta 10 gr. ♈. Et altitudo poli. et distantia a vertice Z1 vel ZA. Quaeritur quot horis post primam observationem sol fuerit in meridiano.

Ex ephemeride datur arcus eclipticae BA, et ex tabula ascensionum rectarum dabitur proinde arcus aequatoris GH³⁾ arcui BA

1) La Pièce A est empruntée aux p. 241-242 du Manuscrit C écrites entre février et mai 1668. Comparez sur des calculs de ce genre, où toutefois il n'est pas encore tenu compte du déplacement du soleil dans l'écliptique, l'avant-dernier alinéa de la p. 222 et le premier alinéa de la p. 226 du T. XVII.

2) Le point 1 (Fig. 119) ne désigne pas l'endroit où se trouvait le soleil au moment de l'observation matinale: dans la figure cet endroit a été transféré de l'Orient à l'Occident, à égale distance du méridien. Comparez le cinqième alinéa là où il est question du ‘duplus arcus QN’.

3) C'est par hasard que dans la Fig. 119 le point H coïncide (ou peu s'en faut) avec l'intersection de l'équateur et de l'écliptique.

[p. 370]

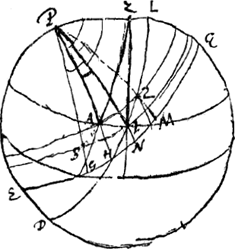
conveniens, unde itaque noscitur angulus BPA. Porro ex 3 lateribus trianguli PAZ¹⁾, invenietur angulus APZ et ex 3 lateribus trianguli P1Z¹⁾ invenietur angulus 1PZ, qui ablatus ab APZ relinquit angulum AP1. cui addito BPA, cognoscitur angulus BP1. Hic vero angulus BP1 mensurat tempus quod elapsum est dum punctum eclipticae 1^2*) pervenit in B. Ponitur autem 1 esse in B cum sol est in A. Itaque 10 horis transierunt meridianum duplus arcus QN et insuper arcus NG. Ergo à 10 horis auferendo tempus quo transijt arcus NG, relinquitur tempus quo transijt duplus arcus QN. cujus itaque temporis dimidium additum horae primae observationis dabit horam qua punctum eclipticae 1 fuit in meridiano. Tunc autem sol nondum est in meridiano, sed adhuc transire debet dimidium ascensionis rectae NM. Ergo addendo tempus hujus dimidij arcus NM ad horam inventam qua punctum 1 erat in meridiano, habebitur hora qua sol erat in meridiano.

Brevius vero sic idem invenitur. Tempus quo punctum eclipticae 2 est in A excedit tempus quo idem punctum 2 erat in circulo P1N^2*) tempore arcus HN. Itaque si a 10 horis, hoc est, a tempore inter duas observationes aequalium solis altitudinum, auferatur tempus arcus HN, relinquetur tempus quo sol aequales angulos horarios confecit ab utraque parte meridiani PQ, utrumque scilicet aequalem ipsi QPN. Cujus temporis semisse itaque à prima observatione sol pervenit ad meridianum (quandoquidem mutatio ascensionis rectae, dum percurrit exiguum arcum 1, 2, pro motu aequabili haberi potest) adeoque dicti temporis semissis additus horae primae observationis dabit horam qua sol erat in meridiano. Itaque tantum invenire opus est angulum AP1 quem metitur arcus HN.

N.B. datur complementum declinationis primae P1; deinde ex tempore dato 10 horarum cognoscitur locus solis 2, et proinde et complementum declinationis P2 sive PA.

His casibus omnibus quibus P2 arcus major quam P1²⁾ addendum est tempus arcus HN ad horas elapsas inter observationes. tum ut prius summae dimidium additum horae primae observationis dabit horam qua sol erat in meridiano.

1) Les arcs PA et P1, compléments de déclinaisons, sont connus: comparez le troisième alinéa.

1) Les arcs PA et P1, compléments de déclinaisons, sont connus: comparez le troisième alinéa.

2*) Voir la note 2 de la p. 369 qui précède.

2*) Voir la note 2 de la p. 369 qui précède.

2) Les ‘casus omnes’ où P2 > P1 se rapportent à quelques autres figures dans le genre de la Fig. 119.

B. Pour mettre dans l'instruction³⁾.

3) La Pièce B est empruntée aux p. 20-21, datant de septembre 1668, du Manuscrit D. Comparez la p. 195 du T. XVII sur l'intention de Huygens de publier une traduction française retouchée de son ‘Kort Onderwijs aengaende het gebruyck der Horologien etc.’ de 1665 (T. XVII).

[p. 371]

Il faut dans le vaisseau suspendre les horologes dans la chambre du Capitaine ou autre lieu commode qui soit bien sec et les defendre autant qu'on peut de la poussiere sans avoir egard que ce soit pres du grand mast ou non puisqu'on a veu par experience que la difference pour le mouvement n'est pas considerable.

Puis que l'anneau graduè ne peut pas servir, ni l'arbaleste ordinaire avec assez d'exactitude, il faudra faire un quartier Anglois⁴⁾ selon les avis qu'en donneront de Combe⁵⁾ et la Voye⁶⁾. Mais il faudra se servir le plus qu'on peut du coucher et lever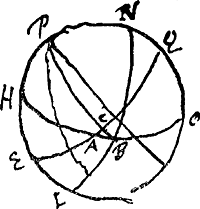 du soleil, parce que ces observations sont incomparablement plus certaines que toutes celles qu'on scauroit faire avec les instruments⁷⁾. Si on peut avoir le lever et le coucher en un jour l'on s'en peut servir sans aucun calcul d'heure par les triangles. Mais si l'on n'a que l'un ou l'autre, l'on supputera l'heure du coucher ou lever par la declinaison du soleil connue et par la hauteur meridiene qu'on ne doibt pas manquer d'observer et qui se prend assez precisement. Ce calcul se fait par le triangle rectangle BCA [Fig. 120], dont l'angle C que fait le meridien⁸⁾ PB (passant par B lieu du soleil) fait [sic] avec l'Equateur EQ. Et l'angle BAC est la hauteur meridiene du

4) D'après une note à la p. 334 de l'édition de 1880 des ‘Voyages and works of John Davis the Navigator’ (London, Hakluyt Society’): ‘The back staff, invented by Davis, was the forerunner of Davis's quadrant, called by the French ‘Quartier Anglais’. Ces instruments servent à mesurer la hauteur du soleil en lui tournant le dos. L'ouvrage ‘The Seamans Secrets’ par John Davis parut en 1594: il n'existe aujourd'hui, paraît-il, que des exemplaires de la deuxième édition de 1607 (London, Th. Dawson). À la p. 334 nommée (les ‘Seamans Secrets’ occupent les p. 229-337) on trouve une figure représentant l'instrument primitif. Le ‘quartier anglais’ est représenté à la p. 356 du Vol. I de l'ouvrage ‘Early Science in Oxford’ par R.T. Gunther (Oxford, printed for the subscribers, 1923). On peut le voir à Leiden dans le ‘Ned. hist. natuurw. Museum’. Il est représenté aussi, sous une forme légèrement différente, à la p. 14 de l'ouvrage de W.J. Blaeu ‘De groote Zeespiegel, inhoudende een korte Onderwijsinge in de Konst der Zeevaert etc.’ (Amsterdam, J. Blaeu, MDCLV). Blaeu l'appelle ‘omgekeerden Graedboogh ofte dubbelden dryhoeck..... daer van den eenen 60 en den anderen 30 graden begrypt’.
Dans son ‘Kort Onderwijs’ de 1665 Huygens ne fait pas encore mention de cet instrument: comparez le deuxième alinéa de la p. 197 du T. XVII. Voir les Additions et Corrections à la fin du présent Tome sur quelques figures de Huygens relatives à ce sujet qu'on trouve plus loin.

5) Il s'agit sans doute de ‘de Combes’ mentionné aussi par Huygens en février 1668 (voir la note 1 de la p. 24 qui précède). À la p. 223 du Manuscrit F, datant de 1685 ou 1686, on trouve quatre noms parmi lesquels figure celui de ‘Francois de Combe’. Il paraît probable que le prénom était en effet François et non pas Francesco (p. 614 du T. VI).

6) Voir la Pièce C qui suit.

7) Comparez la note 2 de la p. 218 du T. XVII.

8) Lisez: ‘cercle de déclinaison’. Il faut pourtant remarquer que, du moins en anglais, le mot ‘meridian’ a parfois un sens plus général. Davis p.e. à la p. 293 de l'ouvrage cité dans la note 4, appelle ‘Eclipticall Meridian’ un grand cercle quelconque passant par les pôles de l'écliptique.

[p. 372]

soleil¹⁾ ou le complement de la hauteur du Pole. Et le costè CB la declinaison du soleil¹⁾. d'ou l'on calcule le costè AC, arc de l'equateur. lequel on adjoute à 90 degr. quand les jours sont plus longs que de 12 heures, ou on l'oste des mesmes 90 deg. quand les jours sont plus courts que de 12 heures. Et on convertit cette somme ou difference en heures. disant .....²⁾.

On pourroit avoir des tables pour les heures du lever et du coucher du soleil dans toute l'annee et pour toutes elevations de pole de degrè en degrè.

Pour ajuster les horologes quand le vaisseau est a la rade ou au port, il ne faut pas porter les horologes a terre. parce qu'en les remettant dans leur boetes pour les raporter au vaisseau on doit apprehender que tous ces remuemens ne les alterent et que les suspendant dans le vaisseau elles³⁾ ne conservent precisement la mesme mesure qu'ils³⁾ avoient sur tetre. Il vaut donc mieux de les laisser suspendues³⁾ dans le vaisseau, et d'aller observer seulement a terre quelque azimut d'estoile fixe par des filets, ou quelque coin de maison, avec un point fixe d'ou l'on regarde⁴⁾, et a l'instant que l'estoile y joint faire signe⁵⁾ avec du feu ou par un coup de pistolet ou de mousquet a celuy qui regarde l'horologe dans le vaisseau afin qu'il marque l'heure qu'elle montre. et le lendemain ou quelques jours apres ayant fait la mesme observation avec la mesme estoile l'on connoistra la difference journaliere de l'horologe, comme il est dit dans l'instruction⁶⁾.

Quand on ne scauroit pas precisement la difference journaliere des horologes, il ne faut pas laisser de faire les observations des Longitudes parce qu'on pourra par apres rechercher cette difference journaliere et redressant par la les observations precedentes voir l'effet des horologes et mesme les veritables differences de Longitude des terres qu'on aura rencontrees.

1) ∠ BAC, complément de la hauteur du pôle, représente la hauteur méridienne du soleil non pas dans le cas considéré dans la Fig. 120, mais dans celui où le soleil se trouve dans l'equateur. Il est évident qu'il ne s'agit pas ici d'une erreur, mais seulement d'une expression peu heureuse. CB est la déclinaison du soleil de la figure.

1) ∠ BAC, complément de la hauteur du pôle, représente la hauteur méridienne du soleil non pas dans le cas considéré dans la Fig. 120, mais dans celui où le soleil se trouve dans l'équateur. Il est évident qu'il ne s'agit pas ici d'une erreur, mais seulement d'une expression peu heureuse. CB est la déclinaison du soleil de la figure.

2) Phrase inachevée. On obtient ainsi l'heure de l'horloge correspondant au temps où le soleil se trouvait dans le méridien.

3) Chez Huygens le mot ‘horologe’ est généralement féminin: mais il n'en est pas toujours ainsi de son temps; voir p.e. les p. 420 du T. II, 399 du T. III (lettres de P. Petit) et 193 du T. XVII.

3) Chez Huygens le mot ‘horologe’ est généralement féminin: mais il n'en est pas toujours ainsi de son temps; voir p.e. les p. 420 du T. II, 399 du T. III (lettres de P. Petit) et 193 du T. XVII.

3) Chez Huygens le mot ‘horologe’ est généralement féminin: mais il n'en est pas toujours ainsi de son temps; voir p.e. les p. 420 du T. II, 399 du T. III (lettres de P. Petit) et 193 du T. XVII.

4) Comparez les p. 106-109 qui précèdent.

5) Comparez, à la p. 501 du T. VI, le huitième alinéa de la Piece C qui suit.

6) Voir la p. 208 du T. XVII, où il est toutefois question d'une détermination de la différence journalière d'une horloge par l'observation du soleil et non pas par celle d'une étoile fixe.

[p. 373]

C. Sur l'Essay des Horologes sur mer par la Voye dans le vaisseau de M. de Beaufort au voiage de Candie en 1669⁷⁾.

[Voir les p. 501-503 du T. VI].

7) La Pièce C a été tirée du Manuscrit D (p. 226-227, datant de septembre 1669).

D. Om te weten hoeveel de dampheffing den opgangh der sonne verhaest of den ondergang verachtert⁸⁾.

Den schrijver van 't Journael heeft de sons center sien opgaen den 9 Julij 1669 als het horologe wees op 2 uren 56′.6″.

En op den 19 Julij daer nae weder het sons center sien opgaen ten 2 uren 52′.28″. Het uren getal der horologien is dan 3′.38″ min als 10 dagen, dat is 9 daghen 23 uren 56′.22″. waer af getrocken het vereffeningh getal van den 9 Jul. dat is 11′.0″ en weder bij gedaen dat van den 19. Jul. te weten 9.58, soo vind men 9 dagen. 23 uren 55′.20″. Dit moet nu gelyck wesen (indien 't horologie wel gestelt was) aen het uren of tijdtgetal der sonne tusschen de twee observatien verloopen. 't Welck aldus gevonden werdt. De bereeckende ure der sons middelpunts opgang den 9 Julij was ten 4 uren 50′ 38″. waer af treckende 2′.54″ die de dampheffing den opgangh doet verhaesten, soo was de sightbare opgangh des centers ten 4 ur. 47′44″⁹⁾.

Wederom den 19 Jul. was des sons middelpunts berekende opgangh ten 4 ur. 56′2″. waer af treckende 2′.54″ voor de verhaesting der opgangh door de dampheffing komt de sichtbaere opgangh des centers ten 4 ur. 53′.8″. Hier af nu getrocken de voorgaende 4 ur. 47′.44″, soo komt voor het tijdtgetal der sonne tusschen de twee observatiën boven de 10 dagen, noch 5′.24″. Maer het tijdtgetal van 't horologie was gevonden 9 dag. 23 ur. 55′.20″ soo is dit minder als der sonne tijdtgetal om 10′.4″. dat is de daghelijckse verachteringh der horologie 1′ 4/10″. men konde de 2′54″ van de verhaesting der sonnen opgangh beijde de dagen achter laten. maer niet indien men den tijdt genomen hadt van een opgangh der sonne tot een ondergangh.

De getallen onder malkander te stellen¹⁰⁾.

8) Traduction: ‘Pour savoir combien l'élévation apparente due aux vapeurs avance le lever ou retarde le coucher du soleil’.
La Pièce D, comme la Pièce C, contient des remarques de Huygens sur le rapport de de la Voye que nous ne possédons plus. Elle est empruntée à la p. 215 du Manuscrit F. La p. 209 date du 20 octobre 1685 et la p. 227 du 5 mai [1686]; comparez la note 10.

9) En marge: men kan seggen, de berekende en door de dampheffing gecorrigeerde ure des opganghs was &c.

10) Voir la p. 61 du T. IX. En 1686 - comparez la note 8 - Huygens se servit, comme on voit, de quelques données du rapport de de la Voye dans la composition de la nouvelle Instruction de cette année (T. IX, p. 55-76). On trouve plus loin dans le présent Tome la traduction d'une partie de cette Instruction; voir les Additions et Corrections.