Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695
(1934)–Christiaan Huygens–
[pagina 242]
| |||||||||||||||||||||||||||||||||||
Quatrième partie de l'horloge à pendule.
| |||||||||||||||||||||||||||||||||||
[pagina 243]
| |||||||||||||||||||||||||||||||||||
Horologii oscillatoriiGa naar margenoot+ Pars Quarta.
| |||||||||||||||||||||||||||||||||||
[pagina 244]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ difficiles que ceux-là; j'ai même enfin trouvé une méthode générale pour chercher la place de ce centre dans les lignes, les surfaces et les corps solidesGa naar voetnoot1). D'où j'ai retiré - outre le plaisir de trouver ce qui avait été longuement recherché par autrui et d'apprendre à connaître dans ces matières les lois et décrets de la nature - l'avantage de savoir désormais mettre au point l'horloge d'après une méthode facile et sûre. Un deuxième résultat qui me semble plus important c'est que je puis, en me basant sur cette théorie, donner une définition très exacte d'une longueur déterminée et restant invariable dans le cours des siècles; on la trouvera à la fin de cette partie. | |||||||||||||||||||||||||||||||||||
Définitions.I.Appelons pendule une figure quelconque douée de pesanteur, que ce soit une ligne, une surface ou un corps solide, suspendue de telle manière qu'elle peut par la force de sa gravité continuer son mouvement réciproque autour d'un point ou plutôt autour d'un axe supposé parallèle à l'horizon. | |||||||||||||||||||||||||||||||||||
II.Donnons à cet axe horizontal autour duquel se fait par hypothèse le mouvement du pendule, le nom d'axe d'oscillation. | |||||||||||||||||||||||||||||||||||
III.Appelons pendule simple celui qui est censé consister en un fil, ou ligne inflexible, dépourvu de pesanteur, et portant en bas un poids qui y est attaché; poids dont la gravité doit être considérée comme recueillie pour ainsi dire en un seul point. | |||||||||||||||||||||||||||||||||||
IV.Appelons pendule composé celui qui consiste en plusieurs poids gardant des distances invariables tant entre elles que de l'axe d'oscillation. Toute figure suspendue pesante de forme quelconque peut donc être appelée un pendule composé, puisqu'elle est divisible par la pensée en un nombre quelconque de parties. | |||||||||||||||||||||||||||||||||||
V.Appelons pendules isochrones ceux dont les oscillations, par des arcs semblables, sont exécutés dans des temps égaux. | |||||||||||||||||||||||||||||||||||
VI.Appelons plan d'oscillation le plan perpendiculaire à l'axe d'oscillation qui est censé passer par le centre de gravité de la figure suspendue. | |||||||||||||||||||||||||||||||||||
[pagina 245]
| |||||||||||||||||||||||||||||||||||
illis difficiliora reperi, & | viam denique, qua in lineis, superficiebus, solidisque corporibusGa naar margenoot+ certa ratione centrum illud investigare liceretGa naar voetnoot1). Unde quidem, praeter voluptatemGa naar margenoot+ inveniendi quae multum ab aliis quaesita fuerant, cognoscendique in his rebus naturae leges decretaque, utilitatem quoque eam cepi, cujus gratia primo animum ad haec applicueram, reperta illa horologii temperandi ratione facili & expedita. Accessit autem hoc quoque, quod pluris faciendum arbitror, ut certae, saeculisque omnibus duraturae, mensurae definitionem absolutissimam per haec tradere possem; qualis est ea quae ad finem horum adjecta reperietur. | |||||||||||||||||||||||||||||||||||
II.Axis ille horizontis plano parallelus, circa quem penduli motus fieri intelligitur, dicatur axis Oscillationis. | |||||||||||||||||||||||||||||||||||
III.Pendulum simplex dicatur quod filo vel linea inflexili, gravitatis experte, constare intelligitur, ima sui parte pondus affixum gerente; cujus ponderis gravitas, velut in unum punctum collecta, censenda est. | |||||||||||||||||||||||||||||||||||
IV.Pendulum verò compositum, quod pluribus ponderibus constat, immutabiles distantias servantibus, tum inter se, tum ab axe Oscillationis. Hinc figura quaelibet suspensa, ac gravitate praedita, pendulum compositum dici potest, quatenus cogitatu in partes quotlibet est divisibilis. | |||||||||||||||||||||||||||||||||||
V.Pendula isochrona vocentur, quorum Oscillationes, per arcus similes, aequalibus temporibus peraguntur. | |||||||||||||||||||||||||||||||||||
VI.Ga naar margenoot+Planum Oscillationis dicatur illud, quod per centrum gravitatis figurae suspensae duci intelligitur, ad axem oscillationis rectum. | |||||||||||||||||||||||||||||||||||
[pagina 246]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ VII.Appelons ligne du centre une droite perpendiculaire à l'axe d'oscillation et passant par le centre de gravité de la figure. | |||||||||||||||||||||||||||||||||||
VIII.Appelons ligne verticale une droite tirée de l'axe d'oscillation, dans le plan d'oscillation, perpendiculairement au plan de l'horizon. | |||||||||||||||||||||||||||||||||||
IX.Appelons centre d'oscillation ou d'agitation d'une figure quelconque un point situé sur la ligne du centre et distant de l'axe d'oscillation d'une longueur égale à celle du pendule simple isochrone avec la figure. | |||||||||||||||||||||||||||||||||||
X.Appelons axe de gravité une droite quelconque passant par le centre de gravité de la figure. | |||||||||||||||||||||||||||||||||||
XI.Qu'une figure plane ou une ligne située dans un plan soit dite osciller ‘in planum’ (exécuter une oscillation plane) lorsque l'axe d'oscillation est situé dans le même plan que la figure ou la ligne. | |||||||||||||||||||||||||||||||||||
XII.Que la figure ou la ligne plane soit dite osciller ‘in latus’ (exécuter une oscillation latérale) lorsque l'axe d'oscillation est perpendiculaire à son plan. | |||||||||||||||||||||||||||||||||||
XIII.Lorsque nous dirons que des poids sont multipliés par des lignes droites, ceci doit être entendu comme suit: ce sont les nombres ou les lignes qui expriment les quantités des poids et leurs rapports mutuels qui sont ainsi multipliésGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Hypothèses.I.Nous supposons que lorsqu'un nombre quelconque de poids commencent à se mouvoir par leur propre gravité, le centre commun de gravité ne peut s'élever à une hauteur supérieure à celle où il se trouvait au début du mouvementGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
[pagina 247]
| |||||||||||||||||||||||||||||||||||
VII.Ga naar margenoot+Linea centri, recta quae per centrum gravitatis figurae ducitur, ad axem oscillationis perpendicularis. | |||||||||||||||||||||||||||||||||||
VIII.Linea perpendiculi, recta in plano oscillationis, ducta ab axe oscillationis, ad horizontis planum perpendicularis. | |||||||||||||||||||||||||||||||||||
IX.Centrum oscillationis vel agitationis figurae cujuslibet, dicatur punctum in linea centri, tantum ab axe oscillationis distans, quanta est longitudo penduli simplicis quod figurae isochronum sit. | |||||||||||||||||||||||||||||||||||
X.Axis gravitatis, linea quaevis recta, per centrum gravitatis figurae transiens. | |||||||||||||||||||||||||||||||||||
XI.Figura plana, vel linea in plano sita, in planum agitari dicatur, cum axis oscillationis in eodem cum figura lineave est plano. | |||||||||||||||||||||||||||||||||||
XII.Eaedem vero in latus agitari dicantur, cum axis oscillationis ad figurae lineaeve planum rectus est. | |||||||||||||||||||||||||||||||||||
XIII.Quando pondera in rectas lineas duci dicentur, id ita est intelligendum, ac si numeri lineaeve, quantitates ponderum rationemque inter se mutuam exprimentes, ita ducanturGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Hypotheses.I.Si pondera quotlibet, vi gravitatis suae, moveri incipiant; non posse centrum gravitatis ex ipsis compositae altius, quam ubi incipiente motu reperiebatur, ascendereGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
[pagina 248]
| |||||||||||||||||||||||||||||||||||
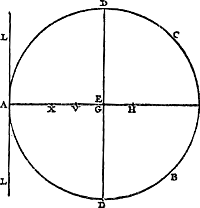
Ga naar margenoot+ Il faut dans ces choses considérer la hauteur suivant la distance d'un plan horizontal et admettre que les corps pesants tâchent de descendre sur ce plan en suivant des droites verticales, c.à.d. perpendiculaires à lui. Ce qui est ou expressément supposé par tous ceux qui ont traité du centre de gravité ou bien doit être suppléé par les lecteurs, puisque sans cela la considération d'un centre de pesanteur n'a pas de sens. Or, pour que notre hypothèse ne fasse scrupule à personne, nous montrerons qu'elle ne signifie que ce que nul n'a jamais nié, savoir que les corps graves ne montent pas d'eux-mêmes. Car premièrement, si nous nous proposons un seul corps grave, il est hors de doute que celui-ci ne peut s'élever par la seule force de sa gravité: nous entendons qu'il s'élève lorsque son centre de gravité monte. Mais la même chose doit nécessairement être admise pour un nombre quelconque de poids attachés l'un à l'autre par des lignes inflexibles, puisque rien n'empêche de les considérer comme un seul poids. Par conséquent le centre commun de gravité de ceux-ci aussi ne pourra monter de lui-même. Que si nous considérons un nombre quelconque de poids non attachés les uns aux autres, nous savons que ceux-là aussi possèdent un centre commun de gravité. Je dis que c'est la hauteur de ce centre qui doit être considérée comme celle de la gravité composée, puisque tous les poids peuvent être amenés à se trouver à cette hauteurlà sans qu'il faille appeler à l'aide aucune autre puissance que celle qui se trouve dans les poids eux-mêmes: il suffit de les joindre arbitrairement par des lignes inflexibles et de les mouvoir autour du centre de gravité, ce à quoi il n'est besoin d'aucune force ou puissance déterminée. C'est pourquoi, de même qu'il ne peut pas arriver que des poids placés dans le même plan horizontal s'élèvent tous également, par la force de la gravité, au-dessus de ce plan, de même aussi le centre de gravité d'un nombre quelconque de poids, disposés de quelque façon que ce soit, ne peut atteindre une plus grande hauteur que celle qu'il a. Or, c'est de la manière suivante qu'on peut démontrer que des poids quelconques peuvent être amenés sans l'application d'aucune force dans le plan horizontal passant par leur centre commun de gravité. Soient [Fig. 76] les poids A, B et C, de position donnée; et soit D leur centre commun de gravité. Supposons mené par lui le plan horizontal dont EF soit une section droite. Que DA, DB, DC soient des lignes inflexibles joignant les poids entre eux d'une manière invariable. Mettons maintenant les poids en mouvement jusqu'à ce que A se trouve en E dans le plan EF. Toutes les verges ayant tourné du même angle, B sera maintenant en G et C en H. Supposons ensuite B en C joints par la verge HG coupant le plan EF en F, où se | |||||||||||||||||||||||||||||||||||
[pagina 249]
| |||||||||||||||||||||||||||||||||||
Altitudo autem in his secundum distantiam à plano horizontali consideratur, graviaqueGa naar margenoot+ ponuntur ad hoc planum, secundum rectas ipsi perpendiculares, descendere conari.Ga naar margenoot+ Quod idem ab omnibus, qui de centro gravitatis egerunt, vel ponitur expresse, vel à legentibus supplendum est, cum absque eo centri gravitatis consideratio locum non habeat. Ipsa vero hypothesis nostra quominus scrupulum moveat, nihil aliud sibi velle eam ostendemus, quam quod nemo unquam negavit, gravia nempe sursum non ferri. Nam primo, si unum quodpiam corpus grave proponamus, illud vi gravitatis suae altius ascendere non posse extra dubium est. ascendere autem tunc intelligitur scilicet, cum ejus centrum gravitatis ascendit. Sed & idem de quotlibet ponderibus, inter se per lineas inflexiles conjunctis, concedi necesse est, quoniam nihil vetat ipsa tanquam unum aliquod considerari. Itaque neque horum commune gravitatis centrum ultro ascendere poterit. Quod si jam pondera quotlibet non inter se connexa ponantur, illorum quoque aliquod commune centrum gravitatis esse scimus. Cujus quidem centri quanta erit altitudo, tantam ajo & gravitatis ex omnibus compositae altitudinem censeri debere; siquidem omnia ad eandem illam centri gravitatis altitudinem deduci possunt, nullâ aliâ accersitâ potentiâ quam quae ipsis ponderibus inest, sed tantum lineis inflexilibus ea pro lubitu conjungendo, ac circa gravitatis centrum movendo; ad quod nulla vi neque potentia determinata opus est. Quare, sicut fieri non potest ut pondera quaedam, in plano eodem horizontali posita, supra illud planum, vi gravitatis suae, omnia aequaliter attollantur; ita nec quorumlibet ponderum, quomodocunque dispositorum, centrum gravitatis ad majorem quam habet altitudinem pervenire poterit. Quod autem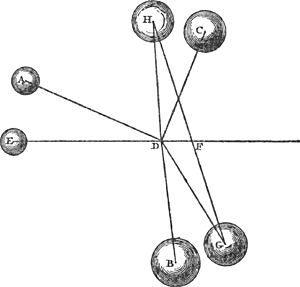 diximus pondera quaelibet, nulla adhibita vi, ad planum horizontale, per centrum commune gravitatis eorum transiens, perduci posse, sic ostendetur.
diximus pondera quaelibet, nulla adhibita vi, ad planum horizontale, per centrum commune gravitatis eorum transiens, perduci posse, sic ostendetur.
Sint pondera A, B, C [Fig. 76], positione data, quorum commune gravitatis centrum sit D. per quod planum horizontale ductum ponatur, cujus sectio recta EF. Sint jam lineae inflexiles DA, DB, DC, quae pondera sibi invariabiliter connectant; quae porro moveantur, donec A sit in plano EF ad E. Virgis vero omnibus per aequales angulos delatis, erunt jam B in G, & C in H. Rursus jam B & C connecti intelligantur virgâ HG, quae secet planum | |||||||||||||||||||||||||||||||||||
[pagina 250]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ trouvera aussi nécessairement le centre de gravité de l'ensemble de ces deux poids, puisque D est celui des trois corps placés en E, G et H et que celui du corps E se trouve aussi dans le plan EDF. Les poids H et G sont maintenant de nouveau mis en mouvement autour du point F comme autour d'un axe et amenés sans aucune force à se trouver simultanément dans le plan EF, de sorte qu'il apparaît que les trois poids, qui étaient d'abord en A, B et C ont été transportés précisément à la hauteur de leur centre de gravité D par leur propre équilibre. C. Q. F. D. La démonstration est la même pour un nombre quelconque d'autres poids. Or, l'hypothèse que nous avons faite s'applique aussi aux corps liquides. Par elle non seulement tout ce qu'Archimède a des corps flottants peut être démontré, mais aussi beaucoup d'autres théorèmes de mécanique. Et véritablement, si les inventeurs de nouvelles machines qui s'efforcent vainement d'obtenir le mouvement perpétuel, savaient faire usage de cette hypothèse, ils decouvriraient aisément eux-mêmes leurs erreurs et comprendraient que ce mouvement ne peut aucunement être obtenu par des moyens mécaniquesGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
II.Nous supposons que, la résistance de l'air et tout autre empêchement manifeste étant absents, comme nous voulons que cela soit entendu dans les démonstrations qui suivent, le centre de gravité du pendule oscillant parcoure des arcs égaux en descendant et en montantGa naar voetnoot2).
Ceci a été démontré pour le pendule simple dans la Prop. IX de la Chute des Corps pesants. Mais l'expérience fait voir que la même chose est vraie pour le pendule composé, de sorte que, quelle que soit la forme du pendule, il est trouvé également capable de rester en mouvement sinon en tant qu'il est plus ou moins empêché par la rencontre de l'air. | |||||||||||||||||||||||||||||||||||
Proposition I.Lorsqu'un nombre quelconque de poids se trouvent du même côté d'un plan et qu'on mène à partir du centre de gravité de chacun d'eux une perpendiculaire à lui, la somme des produits de chaque perpendiculaire par le poids correspondant sera égale à celui de la perpendiculaire menée du centre de gravité de tous les poids au plan considéré, par la somme de ceux-ci.
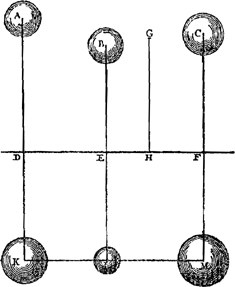
Considérons [Fig. 77] les poids A, B, C situés du même côté d'un plan dont DF est une section droite et menons à ce plan à partir des différents poids les perpendiculaires AD, BE et CF. Que le point G soit le centre de gravité de tous les poids A, B, C; tirons à partir de lui la normale GH au même plan. Je dis que la somme des produits obtenus en multipliant chaque poids par sa perpendiculaire est égale au produit de la droite GH par la somme des poids A, B, C. | |||||||||||||||||||||||||||||||||||
[pagina 251]
| |||||||||||||||||||||||||||||||||||
EF in F; ubi necessario quoque erit centrum gravitatis bino|rum istorum ponderumGa naar margenoot+ connexorum, cum trium, in E, G, H, positorum, centrum gravitatis sit D, & ejusGa naar margenoot+ quod est in E, centrum gravitatis sit quoque in plano EDF. Moventur igitur rursus pondera H, G, super puncto F, velut axe, absque vi ulla, ac simul utraque ad planum EF adducuntur, adeo ut jam tria, quae prius erant in A, B, C, ad ipsam sui centri gravitatis D altitudinem, suo ipsorum aequilibrio, translata appareat. quod erat ostendendum. Eademque de quotcunque aliis est demonstratio. Haec autem hypothesis nostra ad liquida etiam corpora valet, ac per eam non solum omnia illa, quae de innatantibus habet Archimedes, demonstrari possunt, sed & alia pleraque Mechanicae theoremata. Et sanè, si hac eadem uti scirent novorum operum machinatores, qui motum perpetuum irrito conatu moliuntur, facile suos ipsi errores deprehenderent, intelligerent que rem eam mechanica ratione haudquaquam possibilem esseGa naar voetnoot1) | |||||||||||||||||||||||||||||||||||
II.Remoto aëris, alioque omni impedimento manifesto, quemadmodum in sequentibus demonstrationibus id intelligi volumus, centrum gravitatis penduli agitati, aequales arcus descendendo ac ascendendo percurrereGa naar voetnoot2).
De pendulo simplici hoc demonstratum est propositione 9 de Descensu gravium. Idem vero & de composito tenendum esse declarat experientia; siquidem, quaecunque fuerit penduli figura, | aeque apta continuando motui reperitur, nisi in quantum plusGa naar margenoot+ minusve aëris objectu impeditur. | |||||||||||||||||||||||||||||||||||
Propositio I.Ponderibus quotlibet ad eandem partem plani existentibus, si à singulorum centris gravitatis agantur in planum illud perpendiculares; hae singulae in sua pondera ductae, tantundem simul efficient, ac perpendicularis, à centro gravitatis ponderum omnium in planum idem cadens, ducta in pondera omnia.
Sint pondera A, B, C [Fig. 77], sita ad eandem partem plani, cujus sectio recta DF, inque ipsum à singulis ponderibus ducantur perpendiculares AD, BE, CF. Sit autem G punctum centrum gravitatis ponderum omnium A, B, C, à quo ducatur perpendicularis in idem planum GH. Dico summam productorum, quae fiunt à singulis ponderibus in suas perpendiculares, aequari producto ab recta GH in omnia pondera A, B, C. | |||||||||||||||||||||||||||||||||||
[pagina 252]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ En effet, supposons toutes les perpendiculaires provenant des différents points prolongées de l'autre côté du plan DF et soient DK, EL et FM chacune égale à HG; que chacune de ces lignes représente une verge inflexible parallèle à l'horizon, et supposons placés en K, L, M des corps graves tels que chacun d'eux fasse équilibre, par rapport à l'intersection avec le plan DEF, avec le corps grave opposé A, B ou C. L'ensemble des corps K, L, M sera donc en équilibre avec celui des corps A, B, C. Mais on aura: AD : DK = poids K: poids A, et par conséquent DA multipliée par la grandeur A sera égale à DK ou GH multipliée par K. Pareillement EB multipliée par B sera égale à EL ou GH multipliée par L; et FC multipliée par C sera égale à FM ou GH multipliée par M. Par conséquent la somme des produits AD × A, BE × B, CF × F sera égale à celle de GH par chacun des poids K, L, M. Mais comme K, L, M sont en équilibre avec A, B, C séparément, ils seront aussi en équilibre avec les mêmes poids A, B, C suspendus en leur centre de gravité. Il s'ensuit, puisque la distance GH est égale à chacune des distances DK, EL, FH, que la somme des grandeurs A, B, C est nécessairement égale à celle de K, L, M. Par conséquent la somme des produits de GH par chacun des poids A, B, C sera aussi égale aux produits DA × A + EB × B + FC × C. C. Q. F. D. Et quoique dans la démonstration les droites AK, BL, CM aient été considérées comme horizontales et le plan comme vertical, il est clair que si tous les éléments sont placés dans une autre position quelconque l'égalité des produits subsiste, toutes les droites étant les mêmes qu'auparavant. La proposition est donc établie. | |||||||||||||||||||||||||||||||||||
Proposition II.Les mêmes choses qu'auparavant étant posées et tous les poids A, B, C [Fig. 77] étant égaux, je dis que la somme de toutes les perpendiculaires AD, BE, CF est égale à la perpendiculaire GH, émanant du centre de gravité, multipliée par le nombre des poids.
En effet, comme la somme des produits de chaque poids par la perpendiculaire correspondante est égale au produit de GH par l'ensemble des poids, et qu'ici, à cause de l'égalité des poids, cette somme de produits est égale au produit d'un seul poids par la somme de toutes les perpendiculaires, et que de plus le produit de GH par l'ensemble des poids est égal à celui d'un seul poids par la droite GH prise autant de fois qu'il y a de poids, il apparaît que la somme des perpendiculaires est nécessairement égale à GH multipliée par le nombre des poids. C. Q. F. D. | |||||||||||||||||||||||||||||||||||
[pagina 253]
| |||||||||||||||||||||||||||||||||||
 [Fig. 77.]
Intelligantur enim perpendiculares, à singulisGa naar margenoot+ ponderibus eductae, continuari in alteram partem plani DF, sintque singulae DK, EL, FM, ipsi HG aequales; omnesque lineae, inflexiles virgas referant, ad horizontem parallelas; & ponantur in K, L, M, gravitates ejusmodi, quae singulae cum sibi oppositis A, B, C, aequilibrium faciant ad intersectionem plani DEF. Omnes igitur K, L, M, aequiponderabunt omnibus A, B, C. Erit autem, sicut longitudo AD ad DK, ita pondus K ad pondus A, ac proinde DA ducta in magnitudinem A, aequabitur DK, sive GH, ductae in K. Simili|ter EB in B aequabitur EL, siveGa naar margenoot+ GH, in L; & FC in C aequabitur FM, sive GH, in M. Ergo summa productorum ex AD in A, BE in B, CF in F, aequabitur summae productorum ex GH in omnes K, L, M. Quum autem K, L, M, aequiponderent ipsis A, B, C, etiam iisdem A, B, C, ex centro ipsorum gravitatis G suspensis, aequiponderabunt. Unde, cum distantia GH aequalis sit singulis DK, EL, FM, necesse est magnitudines A, B, C, simul sumptas, aequari ipsis K, L, M. Itaque & summa productorum ex GH in omnes A, B, C, aequabitur productis ex DA in A, EB in B, & FC in C. quod erat demonstrandum. Etsi vero in demonstratione positae fuerint rectae AK, BL, CM, horizonti parallelae, & planum ad horizontem erectum; patet, si omnia simul in alium quemlibet situm transponantur, eandem manere productorum aequalitatem, cum rectae omnes sint eaedem quae prius. Quare constat propositum. | |||||||||||||||||||||||||||||||||||
Propositio II.Positis quae prius, si pondera omnia A, B, C [Fig. 77], sint aequalia; dico summam omnium perpendicularium AD, BE, CF, aequari perpendiculari, à centro gravitatis ductae, GH, multiplici secundum ponderum numerum.
Quum enim summa productorum, à ponderibus singulis in suas perpendiculares, aequetur producto ex GH in pondera omnia; sitque hìc, propter ponderum aequalitatem, summa illa productorum aequalis producto ex uno pondere in summam omnium perpendicularium; itemque productum ex GH in pondera omnia, idem quod productum ex pondere uno in GH, multiplicem secundum ponderum numerum: patet summam perpendicularium necessario jam aequari ipsi GH, multiplici secundum ponderum numerum. quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||
[pagina 254]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Proposition III.Si un certain nombre de grandeurs descendent toutes, ou montent toutes, quoique suivant des distances verticales différentes, leurs changements de niveau multipliés chacun par la grandeur correspondante, donneront une somme de produits égale au changement de niveau du centre commun de gravité de ces grandeurs multiplié par leur somme.
Soient données [Fig. 78] les grandeurs A, B, C qui descendent de A, B,C en D, E, F, ou montent de D, E, F en A, B, C. Et que leur centre commun de gravité, au moment où elles sont en A, B, C, soit à la même hauteur que le point G; mais que ce centre soit à la hauteur du point H lorqu'elles sont en D, E, F. Je dis que la somme des produits de la hauteur AD par A, BE par B, CF par C, est égale au produit de GH par l'ensemble de A, B, C. En effet, considérons un plan horizontal à section droite MP. Puissent AD, BE, CF et GH prolongées le couper en M, N, O, P. Puisqu'alors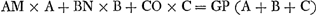 Ga naar margenoot*, et que de même Ga naar margenoot*, et que de même 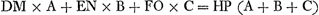 , il s'ensuit que la différence des premiers produits d'avec les deuxièmes est égale à GH (A + B + C). Or, il est manifeste que la dite différence est égale à AD × A + BE × B + CF × C. Cette dernière somme sera donc aussi égale à GH (A + B + C). C. Q. F. D. , il s'ensuit que la différence des premiers produits d'avec les deuxièmes est égale à GH (A + B + C). Or, il est manifeste que la dite différence est égale à AD × A + BE × B + CF × C. Cette dernière somme sera donc aussi égale à GH (A + B + C). C. Q. F. D.
| |||||||||||||||||||||||||||||||||||
Proposition IV.Si un pendule composé de plusieurs poids et commençant son mouvement considéré à partir du repos, a exécuté une partie quelconque de son oscillation entière et qu'on se figure qu'à partir de ce moment, le lien commun étant rompu, chacun de ses poids tourne sa vitesse acquise vers le haut et s'élève à la plus grande hauteur possible, par ce fait le centre commun de gravité remontera à la hauteur qu'il avait avant le commencement de l'oscillation.
Que le pendule [Fig. 79] soit composé de poids en nombre quelconque A, B, C, attachés à une verge ou surface impondérable, et qu'il soit suspendu à un axe passant par le point D perpendiculairement au plan qui est vu ici. Que le centre de gravité des poids A, B, C, soit aussi situé dans ce même plan, et que la ligne du centre DE fasse un angle EDF avec la ligne perpendiculaire DF, bien entendu lorsque le pen- | |||||||||||||||||||||||||||||||||||
[pagina 255]
| |||||||||||||||||||||||||||||||||||
Propositio III.Ga naar margenoot+Si magnitudines quaedam descendant omnes, vel ascendant, licet inaequalibus intervallis; altitudines descensus vel ascensus cujusque, in ipsam magnitudinem ductae, efficient summam productorum aequalem ei, quae fit ex altitudine descensus vel ascensus centri gravitatis omnium magnitudinum, ducta in omnes magnitudines. 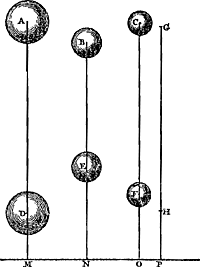 [Fig. 78.]
Sunto magnitudines A, B, C [Fig. 78], quaeGa naar margenoot+ ex A, B, C, descendant in D, E, F; vel ex D, E, F, ascendant in A, B, C. Sitque earum centrum gravitatis omnium, dum sunt in A, B, C, eadem altitudine cum puncto G; cum vero sunt in D, E, F, eadem altitudine cum puncto H. Dico summam productorum ex altitudine AD in A, BE in B, CF in C, aequari producto ex GH in omnes A, B, C. Intelligatur enim planum horizontale cujus sectio recta MP, atque in ipsum incidant productae AD, BE, CF & GH, in M, N, O, P. Quia igitur summa productorum ex AM in A, BN in B, CO in C, aequalis est facto ex GP in omnes A, B, CGa naar margenoot*. Similiterque summa productorum ex DM in A, EN in B, FO in C, aequalis facto ex HP in omnes A, B, C; sequitur & excessum priorum productorum supra posteriora, aequari facto ex GH in omnes magnitudines A, B, C. Dictum vero excessum aequari manifestum est productis ex AD in A, BE in B, CF in C. Ergo haec simul etiam aequalia erunt producto ex GH in omnes A, B, C. quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||
Propositio IV.Si pendulum è pluribus ponderibus compositum, atque è quiete dimissum, partem quamcunque oscillationis integrae confecerit, atque inde porro intelligantur pondera ejus singula, relicto communi vinculo, celeritates acquisitas sursum convertere, ac quousque possunt ascendere; hoc facto, centrum gravitatis ex omnibus compositae, ad eandem altitudinem reversum erit, quam ante inceptam oscillationem obtinebat.
Sit pendulum [Fig. 79] compositum ex ponderibus quotlibet A, B, C, virgae, velGa naar margenoot+ superficiei pondere carenti, inhaerentibus. Sitque suspensum ab axe per D punctum ducto, qui ad planum, quod hic conspicitur, perpendicularis intelligatur. In quo eodem plano etiam centrum gravitatis E, ponderum A, B, C, positum sit; lineaque centri DE, inclinetur ad lineam perpendiculi DF, angulo EDF: attracto, nimirum, | |||||||||||||||||||||||||||||||||||
[pagina 256]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ dule a été écarté de sa position d'équilibre jusque là. Supposons maintenant qu'on lui permette de suivre son mouvement à partir de cette position et qu'il exécute une partie quelconque de son oscillation, de sorte que les poids A, B, C arrivent en G, H, K. Qu'on se figure que chacun des poids, le lien commun étant rompu, tourne alors sa vitesse vers le haut (ce qui peut arriver par la rencontre de certains plans inclinés) et s'élève à la plus grande hauteur possible, jusqu'en L, M ou N. Soit le point P le centre de gravité de tous les poids lorsqu'ils auront atteint ces positions. Je dis que ce point est à la même hauteur que le point E. Car il est d'abord certain que P n'est pas plus haut que E, d'après la première de nos hypothèses. Mais nous montrerons comme suit qu'il n'est pas non plus situé à une moindre hauteur. En effet, soit d'abord, si cela est possible, P situé plus bas que E et supposons que les poids redescendent en tombant des mêmes hauteurs auxquelles ils sont parvenus en montant, savoir LG, MH, NK. D'où il est clair qu'ils atteindront les mêmes vitesses qu'ils avaient en commençant leur ascensionGa naar margenoot*, c.à.d. celles qu'ils avaient acquises par le mouvement du pendule de CBAD en KHGD. Par conséquent, si on les rapporte maintenant avec les dites vitesses à la verge ou surface qui les soutenait, qu'ils s'y attachent simultanément et continuent le mouvement suivant les arcs commencés - ce qui arrivera si, avant d'atteindre la verge, ils rebondissent, comme on peut se le figurer, des plans inclinés QQ -, le pendule ainsi restitué absoudra la partie restante de son oscillation de la même manière que s'il eût continué son mouvement sans aucune interruption. De sorte que le centre de gravité E du pendule parcourt en descendant et en montant des arcs égaux EF, FR et se trouve donc en R à la même hauteur qu'en E. Mais nous avons posé que E serait plus élevé que F, centre de gravité des poids situés en L, M, N. Par conséquent R sera aussi plus élevé que P: le centre de gravité des poids qui sont tombés de L, M, N se serait donc élevé à une hauteur supérieure à celle dont il était descendu, ce qui est absurdeGa naar margenoot*. Le centre de gravité P n'est donc pas situé plus bas que | |||||||||||||||||||||||||||||||||||
[pagina 257]
| |||||||||||||||||||||||||||||||||||
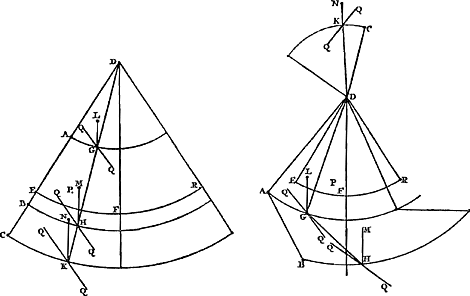 [Fig. 79.]Ga naar margenoot+
eo usque pendulo. Hinc vero dimitti jam ponatur, ac partem quamlibet oscillationis conficere, ita ut pondera A, B, C, perveniant in G, H, K. Unde, relicto deinceps communi vinculo, singula intelligantur acquisitas celeritates sursum convertere, (quod impingendo in plana quaedam inclinata, fieri poterit,) & quousque possunt ascendere, nempe in L, M, N. Quo ubi pervenerint, sit centrum gravitatis omnium punctum P. Dico hoc pari altitudine esse cum puncto E. Nam primum quidem, constat P non altius esse quam E, ex prima sumptarum hypothesium. Sed nec humilius fore sic ostendemus. Sit enim, si potest, P humilius quam E, & intelligantur pondera ex iisdem, ad qua ascenderunt, altitudinibus recidere, quae sunt LG, MH, NK. Unde quidem easdem celeritates ipsis acquiri constat, quas habebant ad ascendendum ad istas altitudinesGa naar margenoot*, hoc est, eas ipsas quas acquisierant motu penduli ex CBAD in KHGD. Quare, si cum dictis celeritatibus ad virgam superficiemve, cui innexa fuere, nunc referantur, eique simul adhaerescant, motumque secundum inceptos arcus continuent; quod fiet, si priusquam virgam attingant, à planis inclinatis QQ repercussa intelli|gantur; absolvet, hoc modo restitutum pendulum,Ga naar margenoot+ oscillationis partem reliquam, aequè ac si absque ulla interruptione motum continuasset. Ita ut centrum gravitatis penduli, E, arcus aequales EF, FR, descendendo ac ascendendo percurrat, ac proinde in R eadem ac in E altitudine reperiatur. Ponebatur autem E esse altius quam P centrum gravitatis ponderum in L, M, N, positorum. Ergo & R altius erit quam P: adeoque ponderum ex L, M, N, delapsorum centrum gravitatis, altius, quam unde descenderat, ascendisset. quod est absurdumGa naar margenoot*. | |||||||||||||||||||||||||||||||||||
[pagina 258]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ E. Mais il n'était pas non plus situé à une plus grande hauteur. Il faut donc qu'il soit situé à la même hauteur. C. Q. F. D. | |||||||||||||||||||||||||||||||||||
Proposition V.Etant donné un pendule composé d'un nombre quelconque de poids, si chacun des poids est multiplié par le carré de sa distance à l'axe d'oscillation et que la somme des produits est divisée par le produit de la somme des poids par la distance du centre commun de gravité de tous les poids au même axe d'oscillation, il en résultera la longueur du pendule simple isochrone avec le pendule composé, en d'autres termes la distance entre l'axe et le centre d'oscillation du pendule composéGa naar voetnoot1).
Soient [Fig. 80] les poids A, B, C qui composent le pendule (et dont on ne considère ni la figure ni la grandeur mais seulement la gravité) suspendus à l'axe passant par le point D et supposé perpendiculaire au plan qui est vu ici. Que leur centre commun de gravité E se trouve aussi dans ce plan; car peu importe que les poids soient en des plans divers. Appelons d la distance du point E de l'axe, savoir la droite ED. Soit de même e la distance AD du poids A, f celle de BD et g celle de CD. Or, on trouve, en multipliant chaque point par le carré de sa distance, la somme des produits ae2 + bf2 + cg2. D'autre part, lorsqu'on multiplie la somme des poids par la distance du centre de gravité commun, le produit sera ad + bd + cdGa naar margenoot*. D'où résulte, en divisant le premier produit par le deuxième, 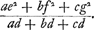
Si l'on égale à cette longueur celle du pendule simple FG, qui sera désignée par x, je dis qu'il sera isochrone avec le pendule composé donné. Supposons en effet le pendule FG et la ligne du centre DE écartés du même angle de la ligne perpendiculaire, le premier de FH et le deuxième de DK, et qu'étant | |||||||||||||||||||||||||||||||||||
[pagina 259]
| |||||||||||||||||||||||||||||||||||
Non igitur centrum gravitatis P humilius est quam E. Sed nec altius erat. Ergo aequeGa naar margenoot+ altum sit necesse est. quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||
Propositio V.Dato pendulo ex ponderibus quotlibet composito, si singula ducantur in quadrata distantiarum suarum ab axe oscillationis, & summa productorum dividatur per id quod fit ducendo ponderum summam, in distantiam centri gravitatis communis omnium ab eodem axe oscillationis; orietur longitudo penduli simplicis composito isochroni, sive distantia inter axem & centrum oscillationis ipsius penduli compositiGa naar voetnoot1).  [Fig. 80.]
Sint [Fig. 80] pondera pendulum componentia, (quorum nec figura nec magnitudo, sed gravitas tantum consideretur), A, B, C, suspensa ab axe, qui per punctum D, ad planum quod conspicitur, rectus intelligitur. In quo plano sit quoque eorum centrum commune gravitatis E; nam pondera in diversis esse nihil refert. Distantia puncti E ab axe, nempe recta ED, vocetur d. Item ponderis A distantia AD, sit e; BD, f; CD, g. Ducendo itaque singula pondera in qua|drata suarum distantiarum,Ga naar margenoot+ erit productorum summa aee + bff + cgg. Et rursus, ducendo summam ponderum in distantiam centri gravitatis omnium, productum aequale erit ad + bd + cdGa naar margenoot*. Unde, productum prius per hoc dividendo, habebitur 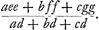
Cui longitudini si aequalis statuatur longitudo penduli simplicis FG, quae etiam x vocabitur; dico hoc illi composito isochronum esse. Ponantur enim tum pendulum FG, tum linea centri DE, aequalibus angulis à linea perpendiculi remota, illud ab FH, haec ab DK, atque inde dimissa librari, & in recta | |||||||||||||||||||||||||||||||||||
[pagina 260]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ abandonnés à eux-mêmes ils commencent leur oscillation à partir de là, et que sur la ligne DE DL soit prise égale à FG. Par conséquent le poids G du pendule FG parcourra en une oscillation entière l'arc GM que la ligne perpendiculaire FH coupera en deux parties égales; et le point L parcourra l'arc LN, semblable et égal à l'autre, que DK divisera par le milieu. De même le centre de gravité E parcourra l'arc semblable EI. Que si nous démontrons, après avoir pris sur les arcs GM, NL des points quelconques qui les divisent de la même manière, tels que O et P, que la vitesse du poids G en O est la même que celle du point L en P, il en résultera que les deux arcs sont parcourus en des temps égaux et que par conséquent le pendule FG est isochrone avec le pendule composé de A, B, C. Or, cela sera démontré comme suit. Soit d'abord, si cela est possible, la vitesse du point L, lorsqu'il est parvenu jusqu'en P, plus grande que celle du poids G en O. Or, il est constant que quand le point L parcourt l'arc LP, le centre de gravité E parcourt en même temps l'arc semblable EQ. Soient tirées vers le haut à partir des points Q, P, O des perpendiculaires qui rencontrent les cordes des arcs EI, LN, GM en R, S, Y. Désignons SP par y. Partant, vu que LD ou x est à ED ou d comme SP ou y est à RQ, RQ sera égale à dy/x. Or, puisque le poids G a en O la vitesse nécessaire pour remonter à la hauteur d'où il est descendu, savoir par l'arc OM ou par la perpendiculaire OY égale à PS, le point L aura, en parvenant à P, une plus grande vitesse qu'il ne lui faut pour monter de PS. Mais tandis que L se déplace jusqu'en P, le poids A, B, C parcourront en même temps des arcs semblables à LP, savoir AT, BV, CX. Et la vitesse du point L en P est à celle du poids A en T, lorsqu'ils sont retenus par le même lien, comme la distance DL est à DA. Mais comme le carré de la vitesse du point L en P est au carré de la vitesse du point A en T, ainsi est la hauteur à laquelle il est possible de monter avec cette vitesse-là à celle où il est possible de monter avec cette vitesse-ciGa naar margenoot*. Par conséquent aussi, comme le carré de la distance DL, c.à.d. x2, est au carré de la distance DA, savoir e2, ainsi est la hauteur où il est possible de monter avec la vitesse du point L parvenu en P (hauteur dont nous avons dit qu'elle est supérieure à PS ou y) à la hauteur qui peut être atteinte avec la vitesse que le poids A possède en T, bien entendu si ce poids, après être parvenu jusqu'en T, pouvait quitter le pendule et diriger séparément son mouvement vers le haut. Cette hauteur sera donc supérieure à e2y/x2. Pour la même raison la hauteur à laquelle s'élèverait le poids B avec la vitesse acquise par le trajet de l'arc BV serait plus grande que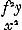 . Et la hauteur à laquelle s'élèverait le poids C avec la vitesse acquise en parcourant l'arc CX serait plus grande que g2y/x2. Par conséquent, chacune de ces hauteurs étant multipliée par le poids cor- . Et la hauteur à laquelle s'élèverait le poids C avec la vitesse acquise en parcourant l'arc CX serait plus grande que g2y/x2. Par conséquent, chacune de ces hauteurs étant multipliée par le poids cor-
| |||||||||||||||||||||||||||||||||||
[pagina 261]
| |||||||||||||||||||||||||||||||||||
DE sumatur DL aequalis FG. Itaque pondus G penduli FG, integra oscillatione arcumGa naar margenoot+ GM percurret, quem linea perpendiculi FH medium secabit. punctum vero L arcum illi similem & aequalem LN, quem medium dividet DK. Itemque centrum gravitatis E, percurret similem arcum EI. Quod si in arcubus GM, NL, sumptis punctis quibuslibet, similiter ipsos dividentibus, ut O & P, eadem celeritas esse ostendatur ponderis G in O, & puncti L in P; constabit inde aequalibus temporibus utrosque arcus percurri, ac proinde pendulum FG, pendulo composito ex A, B, C, isochronum esse. Ostendetur autem hoc modo. Sit primo, si potest, major celeritas puncti L, ubi in P pervenit, quam ponderis G in O. Constat autem, dum punctum L percurrit arcum LP, simul centrum gravitatis E percurrere arcum similem EQ. Ducantur à punctis Q, P, O, perpendiculares sursum, quae occurrant subtensis arcuum EI, LN, GM, in R, S, Y. & SP vocetur y. Unde, cum sit ut LD, x, ad ED, d, ita SP, y, ad RQ; erit RQ aequalis dy/x. Jam quia pondus G eam celeritatem habet in O, qua valet ad eandem unde descendit altitudinem ascendere, nempe per arcum OM, vel perpendicularem OY ipsi PS aequalem; punctum igitur L, ubi in P pervenerit, majorem ibi celeritatem habebit, quam qua ascenditur ad altitudinem PS. Dum vero L transit in P, simul pondera A, B, C, similes arcus percurrunt ipsi LP, nimirum AT, BV, CX. Estque puncti L celeritas in P, ad celeritatem ponderis A in T, quum vinculo eodem contineantur, sicut distantia DL ad DA. Sed ut quadratum celeritatis puncti L, quam habet in P, ad quadratum celeritatis puncti A in T, ita est altitudo ad quam illa celeritate ascendi potest, ad altitudinem quò hac celeritate ascendi potestGa naar margenoot*. Ergo etiam, ut quadratum distantiae DL, quod est xx, ad quadratum distantiae DA, quod est ee, ita est altitudo quo ascenditur celeritate puncti L, quum est in P, (quae altitudo major dicta est quam PS sive y,) ad altitudinem quo ascenditur celeritate ponderis A in T; si nempe postquam in T pervenit, relicto pendulo, | seorsim motum suum sursum converteret. Quae proindeGa naar margenoot+ altitudo major erit quam eey/xx. Eadem ratione, erit altitudo ad quam ascenderet pondus B, celeritate acquisita per arcum BV, major quam ffy/xx. Et altitudo ad quam ascenderet pondus C, celeritate acquisita per arcum CX, major quam ggy/xx. Unde, ductis singulis altitudinibus istis in | |||||||||||||||||||||||||||||||||||
[pagina 262]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ respondant, la somme des produits sera supérieure à 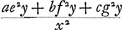 . Nous en conclurons que cette somme est aussi plus grande que . Nous en conclurons que cette somme est aussi plus grande que 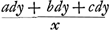 Car puisque la longueur x a été posée égale à Car puisque la longueur x a été posée égale à 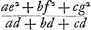 , on aura , on aura 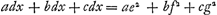 . En tout étant multiplié par y et divisé par x2, on aura . En tout étant multiplié par y et divisé par x2, on aura 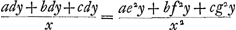 . D'où résulte ce que nous avons dit. Or, cette somme de produits est égale à celle qui s'obtient en multipliant la hauteur à laquelle monte le centre commun de gravité des poids A, B, C par la somme a + b + c de ces poids, bien entendu dans le cas où, comme nous l'avons dit, chacun de ces poids s'élève séparément à la plus grande hauteur possible. Mais le quantité . D'où résulte ce que nous avons dit. Or, cette somme de produits est égale à celle qui s'obtient en multipliant la hauteur à laquelle monte le centre commun de gravité des poids A, B, C par la somme a + b + c de ces poids, bien entendu dans le cas où, comme nous l'avons dit, chacun de ces poids s'élève séparément à la plus grande hauteur possible. Mais le quantité 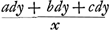 s'obtient aussi comme produit de la
descente du centre de gravité des mêmes poids (laquelle descente est RQ ou dy/x, comme il a été trouvé plus haut) par la même somme des poids a + b + c. Par conséquent, comme il a été démontré que le produit obtenu d'abord est plus grand que ce deuxième, il s'ensuit que l'ascension du centre de gravité des poids A, B, C, lorsque, parvenus en T, V, X, après avoir quitté le pendule, ils dirigent chacun à part les vitesses acquises vers le haut, sera plus grande que la descente du même centre de gravité pendant le mouvement qui les amène de A, B, C en T, V, X. Ce qui est absurde, puisque la dite ascension doit être égale à la descente, d'après la proposition précédente. s'obtient aussi comme produit de la
descente du centre de gravité des mêmes poids (laquelle descente est RQ ou dy/x, comme il a été trouvé plus haut) par la même somme des poids a + b + c. Par conséquent, comme il a été démontré que le produit obtenu d'abord est plus grand que ce deuxième, il s'ensuit que l'ascension du centre de gravité des poids A, B, C, lorsque, parvenus en T, V, X, après avoir quitté le pendule, ils dirigent chacun à part les vitesses acquises vers le haut, sera plus grande que la descente du même centre de gravité pendant le mouvement qui les amène de A, B, C en T, V, X. Ce qui est absurde, puisque la dite ascension doit être égale à la descente, d'après la proposition précédente.
Si l'on dit que la vitesse du point L, quand il sera parvenu en P, est plus petite que celle du poids G parvenu jusqu'en O, nous démontrerons de la même manière que l'ascension possible du centre de gravité des poids A, B, C est plus petite que la descente, ce qui encore une fois ne s'accorde pas avec la proposition précédente. Reste donc que la vitesse du point L transporté jusqu'en P est la même que celle du poids G en O. D'où il résulte, comme nous l'avons dit plus haut, que le pendule simple FG est isochrone avec le pendule composé de A, B, C. | |||||||||||||||||||||||||||||||||||
Proposition VI.Etant donné un pendule composé d'un nombre quelconque de poids égaux, si la somme des carrés des distances des poids à l'axe d'oscillation est divisée par la distance du centre de gravité commun du même axe d'oscillation, cette dernière distance étant multipliée par le nombre des poids, il en résultera la longueur du pendule simple isochrone avec le pendule composéGa naar voetnoot1).
Soient posées les mêmes choses qu'auparavant, mais qu'on se figure tous les poids | |||||||||||||||||||||||||||||||||||
[pagina 263]
| |||||||||||||||||||||||||||||||||||
sua pondera, erit summa productorum major quam 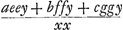 . quae proindeGa naar margenoot+ major quoque probatur quam . quae proindeGa naar margenoot+ major quoque probatur quam 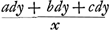 . Nam quia posita est longitudo x aequalis . Nam quia posita est longitudo x aequalis 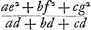 ; erit adx + bdx + cdx aequale aee + bff + cgg. Et ductis omnibus in y, & dividendo per xx, erit ; erit adx + bdx + cdx aequale aee + bff + cgg. Et ductis omnibus in y, & dividendo per xx, erit 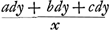 aequale aequale 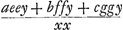 . Unde quod dictum est consequitur. Est autem summa ista productorum aequalis ei, quod sit ducendo altitudinem, ad quam ascendit centrum gravitatis commune ponderum A, B, C, in summam ipsorum ponderum, a + b + c; si nempe singula, uti dictum, seorsim quousque possunt moveantur. Quantitas vero . Unde quod dictum est consequitur. Est autem summa ista productorum aequalis ei, quod sit ducendo altitudinem, ad quam ascendit centrum gravitatis commune ponderum A, B, C, in summam ipsorum ponderum, a + b + c; si nempe singula, uti dictum, seorsim quousque possunt moveantur. Quantitas vero 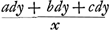 producitur ex descensu centri gravitatis eorundem ponderum, (qui descensus est RQ, sive dy/x, ut supra inventum fuit,) in eandem quoque ponderum summam a + b + c. Ergo quum prius productum altero hoc majus ostensum fuerit, sequitur ascensum centri gravitatis ponderum A, B, C, si, relicto pendulo ubi pervenere in T, V, X, singula celeritates acquisitas sursum convertant, majorem fore ejusdem centri gravitatis descensu, dum ex A, B, C, moventur in T, V, X. quod est absurdum, cum dictus ascensus descensui aequalis esse debeat, per antecedentem. producitur ex descensu centri gravitatis eorundem ponderum, (qui descensus est RQ, sive dy/x, ut supra inventum fuit,) in eandem quoque ponderum summam a + b + c. Ergo quum prius productum altero hoc majus ostensum fuerit, sequitur ascensum centri gravitatis ponderum A, B, C, si, relicto pendulo ubi pervenere in T, V, X, singula celeritates acquisitas sursum convertant, majorem fore ejusdem centri gravitatis descensu, dum ex A, B, C, moventur in T, V, X. quod est absurdum, cum dictus ascensus descensui aequalis esse debeat, per antecedentem.
Eodem modo, si dicatur celeritatem puncti L, ubi pervenerit in P, minorem esse celeritate ponderis G quum in O pervenerit; ostendemus ascensum possibilem centri gravitatis ponderum A, B, C, minorem esse quam descensum, quod eidem propositioni antecedenti repugnat. Quare relinquitur ut eadem sit celeritas puncti L, ad P translati, quae ponderis G in O. Unde, ut superius dictum, sequitur pendulum simplex FG composito ex A, B, C, isochronum esse. | |||||||||||||||||||||||||||||||||||
Propositio VI.Dato pendulo ex quotcunque ponderibus aequalibus composito; si summa quadratorum factorum à distantiis, quibus unumquodque pondus abest ab axe oscillationis, ap|plicetur ad distantiam centri gravitatis communis ab eodem oscillationis axe,Ga naar margenoot+ multiplicem secundum ipsorum ponderum numerum, orietur longitudo penduli simplicis composito isochroniGa naar voetnoot1).
Sint posita eadem quae prius, sed pondera omnia inter se aequalia intelligantur, & | |||||||||||||||||||||||||||||||||||
[pagina 264]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ égaux et que chacun d'eux soit appelé a. Qu'ici aussi il ne leur soit attribué aucune grandeur, mais qu'ils soient considérés quant à la dimension comme extrêmement petits. La longueur du pendule simple isochrone sera donc d'après la proposition précédente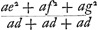 . Ou bien, puisque le numérateur et le dénominateur ont le facteur commun a, la même longueur sera exprimée par . Ou bien, puisque le numérateur et le dénominateur ont le facteur commun a, la même longueur sera exprimée par 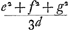 . Cette formule représente la somme des carrés des distances des poids à l'axe d'oscillation, divisée par la distance du centre de gravité de tous ces poids au même axe d'oscillation, cette dernière distance étant multipliée par le nombre des poids qui est ici de trois. En effet, on voit aisément que ce nombre, par lequel il faut multiplier la distance d, correspond nécessairement au nombre des poids. La proposition est donc prouvée. . Cette formule représente la somme des carrés des distances des poids à l'axe d'oscillation, divisée par la distance du centre de gravité de tous ces poids au même axe d'oscillation, cette dernière distance étant multipliée par le nombre des poids qui est ici de trois. En effet, on voit aisément que ce nombre, par lequel il faut multiplier la distance d, correspond nécessairement au nombre des poids. La proposition est donc prouvée.
Que si les poids égaux sont attachés l'un à l'autre par une seule ligne droite suspendue à son extrémité supérieure, il est établi que la distance à l'axe d'oscillation de leur centre commun de gravité, multipliée par le nombre des poids, est égale à la somme des distances de tous les poids du même axe d'oscillationGa naar margenoot*; par conséquent, dans ce cas, on aura aussi la longueur du pendule simple isochrone avec le pendule composé, en divisant la somme des carrés des distances de tous les poids à l'axe d'oscillation par la somme de ces mêmes distances. | |||||||||||||||||||||||||||||||||||
Définition XIV.S'il y a dans le même plan une figure et une ligne droite qui la touche extérieurement, qu'on astreint une autre droite perpendiculaire à ce plan à se mouvoir de manière à couper toujours le contour de la figure, de sorte que cette droite décrit une certaine surface, et qu'on coupe ensuite cette dernière par un plan passant par la dite tangente et incliné par rapport au plan de la figure donnée; nous désignerons le solide compris entre les deux plans et la partie de la surface décrite interceptée par ces plans, par l'expression OngletGa naar voetnoot1) coupé sur cette figure comme base.
Soit, dans la figure ci-ajoutée [Fig. 81], ABEC la figure plane donnée, MD la tangente, EF la génératrice passant par son contour; et l'onglet le corps compris entre les plans ABEC et MFG et la partie de la surface décrite par la droite EF. | |||||||||||||||||||||||||||||||||||
[pagina 265]
| |||||||||||||||||||||||||||||||||||
singula dicantur a. Rursus vero nulla eorum magnitudo consideretur, sed pro minimisGa naar margenoot+ habeantur, quantum ad extensionem. Itaque penduli simplicis isochroni longitudo, per propositionem antecedentem, erit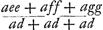 . Vel, quia quantitas divisa ac dividens utraque per a dividitur, fiet nunc eadem longitudo, . Vel, quia quantitas divisa ac dividens utraque per a dividitur, fiet nunc eadem longitudo, 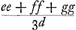 . Quo significatur summa quadratorum à distantiis ponderum ab axe oscillationis, applicata ad distantiam centri gravitatis omnium ab eodem oscillationis axe, multiplicem secundum numerum ipsorum ponderum, qui hic est 3. facile enim perspicitur numerum hunc, in quem ducitur distantia d, respondere necessario ipsi ponderum numero. Quare constat propositum. . Quo significatur summa quadratorum à distantiis ponderum ab axe oscillationis, applicata ad distantiam centri gravitatis omnium ab eodem oscillationis axe, multiplicem secundum numerum ipsorum ponderum, qui hic est 3. facile enim perspicitur numerum hunc, in quem ducitur distantia d, respondere necessario ipsi ponderum numero. Quare constat propositum.
Quod si pondera aequalia in unam lineam rectam conjuncta sint, atque ex termino ejus superiore suspensa; constat distantiam centri gravitatis, ex omnibus compositae, ab axe oscillationis, multiplicem secundum ponderum numerum, aequari summae distantiarum omnium ponderum ab eodem oscillationis axeGa naar margenoot*; ac proinde, hoc casu, habebitur quoque longitudo penduli simplicis, composito isochroni, si summa quadratorum à distantiis ponderum singulorum ab axe oscillationis, dividatur per summam earundem omnium distantiarum. | |||||||||||||||||||||||||||||||||||
Definitio XIV.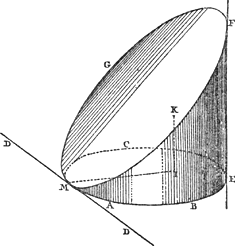 [Fig. 81.]
Si fuerint in eodem plano, figura quaedam, & linea recta quae ipsam extrinsecus tangat; & per ambitum figurae alia recta, plano ejus perpendicularis, circumferatur, superficiemque quandam describat, quae deinde secetur plano per dictam tangentem ducto & ad dictae figurae planum inclinato; solidum comprehensum à duobus planis istis, & parte superficiei descriptae, inter utrumque planum intercepta, vocetur CuneusGa naar voetnoot1) super figura illa, tanquam basi, abscissus.
In schemate adjecto [Fig. 81], est ABEC figura data; recta ea tangens|MD;Ga naar margenoot+ quae vero per ambitum ejus circumfertur, EF; cuneus autem figura solida planis ABEC, MFG, & parte superficiei, à recta EF descriptae, comprehensa. | |||||||||||||||||||||||||||||||||||
[pagina 266]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Definition XV.Appelons Subcentrique de l'onglet la distance entre la droite par laquelle passe le plan qui limite l'onglet et le pied sur la base de l'onglet du perpendiculaire provenant de son centre de gravité.
Dans la même figure [Fig. 81], K étant le centre de gravité de l'onglet, la droite KI la perpendiculaire sur sa base ABEC, et IM une perpendiculaire sur MD, IM sera la droite que nous appelons subcentrique. | |||||||||||||||||||||||||||||||||||
Proposition VII.L'onglet coupé sur une figure plane quelconque par un plan incliné d'un angle demi-droit est égal au solide qui s'obtient par la multiplication de cette figure par une hauteur égale à la distance qui sépare le centre de gravité de la figure plane de la droite par laquelle passe le plan qui limite l'ongletGa naar voetnoot1).
Soit [Fig. 82] un onglet ABD coupé sur la figure plane ACB par un plan incliné d'un angle demi-droit et passant par EE, tangente à la figure ACB située dans son plan. Soit F le centre de gravité de la figure et FA une perpendiculaire abaissée de ce centre sur la droite EE. Je dis que l'onglet ACB est égal au solide obtenu par la multiplication de la figure ACB par une hauteur égale à FA. En effet, supposons la figure ACB divisée en particules égales extrêmement petites et soit G une d'elles. Il est certain que si chacune d'elles est multipliée par sa distance à la droite EE, la somme des produits sera égale à celle qui est obtenue par la multiplication de la droite AF par l'ensemble des particulesGa naar margenoot*, c.à.d. à celle qui résulte de la multiplication de la figure ACB par une hauteur égale à AF. Mais chacune des particules telles que G, multipliée par sa distance GH, est égale à un très petit parallélépipède ou prisme tel que GK élevé sur elle et se terminant à la surface oblique AD; car leurs hauteurs sont égales aux distances GH à cause de l'inclinaison d'un angle demi-droit des plans AD et ACB l'un par rapport à l'autre. Et il est clair que l'onglet ABD entier est formé par ces parallélépipèdes. L'onglet lui-même sera donc égal au solide construit sur la base ACB et ayant une hauteur égale à la droite FA. C. Q. F. D. | |||||||||||||||||||||||||||||||||||
Proposition VIII.Si une ligne droite touche une figure plane, que la figure est supposée divisée en | |||||||||||||||||||||||||||||||||||
[pagina 267]
| |||||||||||||||||||||||||||||||||||
Definitio XV.Ga naar margenoot+Distantia inter rectam, per quam cuneus abscissus est, & punctum baseos, in quod perpendicularis cadit à cunei centro gravitatis, dicatur cunei Subcentrica.
Nempe in figura eadem [Fig. 81], si K sit centrum gravitatis cunei, recta vero KI ad basin ejus ABEC perpendicularis ducta sit, & rursus IM perpendicularis ad MD; erit IM, quam subcentricam dicimus. | |||||||||||||||||||||||||||||||||||
Propositio VII.Cuneus super plana figura qualibet abscissus, plano inclinato ad angulum semirectum, aequalis est solido, quod fit ducendo figuram eandem, in altitudinem aequalem distantiae centri gravitatis figurae, ab recta per quam abscissus est cuneusGa naar voetnoot1). 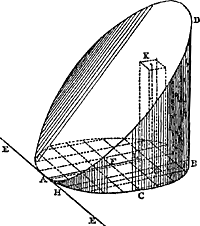 [Fig. 82.]
Sit, super figura plana ACB [Fig. 82], cuneus ABD abscissus plano ad angulum semirectum inclinato, ac transeunte per EE, rectam tangentem figuram ACB, inque ejus plano sitam. Centrum vero gravitatis figurae sit F, unde in rectam EE ducta sit perpendicularis FA. Dico cuneum ACB aequalem esse solido, quod fit ducendo figuram ACB in altitudinem ipsi FA aequalem. Intelligatur enim figura ACB divisa in particulas minimas aequa|les quarum una G. ItaqueGa naar margenoot+ constat, si harum singulae ducantur in distantiam suam ab recta EE, summam productorum fore aequalem ei quod fit ducendo rectam AF in particulas omnesGa naar margenoot*, hoc est, ei quod fit ducendo figuram ipsam ACB, in altitudinem aequalem AF. Atqui particulae singulae ut G, in distantias suas GH ductae, aequales sunt parallelepipedis, vel prismatibus minimis, super ipsas erectis, atque ad superficiem obliquam AD terminatis, quale est GK; quia horum altitudines ipsis distantiis GH aequantur, propter angulum semirectum inclinationis planorum AD & ACB. Patetque ex his parallelepipedis totum cuneum ABD componi. Ergo & cuneus ipse aequabitur solido super basi ACB, altitudinem habenti rectae FA aequalem. quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||
[pagina 268]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ des particules très petites égales entre elles et que de chaque particule une perpendiculaire est abaissée sur cette droite, la somme des carrés de toutes ces perpendiculaires sera égale à un certain rectangle multiplié par le nombre des particules; lequel rectangle a pour côtés la distance du centre de gravité de la figure à la ligne droite et la subcentrique de l'onglet qui est coupé sur la figure donnée par un plan passant par cette droiteGa naar voetnoot1).
En effet, toutes les autres choses étant posées comme dans la construction précédente, soit LA [Fig. 82] la subcentrique de l'onglet ABD par rapport à la droite EE. Il s'agit donc de démontrer que la somme des carrés des distances de toutes les particules de la figure ACB est égale au rectangle formé par FA et LA, multiplié par le nombre des particules. Or, il apparaît par la démonstration précédente que les hauteurs des différents parallélépipèdes telles que GK sont égales aux distances des particules qui constituent leurs bases, telles que G, de la droite AE. C'est pourquoi, si l'on multiplie le parallélépipède GK par la distance GH, c'est comme si l'on multipliait la particule G par le carré de la distance GH. Et la même chose est vraie pour tous les autres parallélépipèdes. Mais la somme des produits de tous les parallélépipèdes chacun par sa distance de la droite AE est égale au produit de l'onglet ABD par la distance LAGa naar margenoot*, puisque l'onglet a son centre de gravité au-dessus du point L. Par conséquent la somme des produits de chacune des particules G par le carré de sa distance à la droite AE sera égale au produit de l'onglet ABD par la droite LA, en d'autres termes au produit de la figure ACB par le rectangle de côtés FA et LA. Car l'onglet ABD est égal au produit de la figure ACB par la droite FAGa naar margenoot*. Derechef, comme la figure ACB est égale au produit d'une particule G par le nombre des particules, il s'ensuit que le dit produit de la figure ACB par le rectangle construit sur FA et LA est égal à celui de la particule G par le rectangle construit sur FA et LA, multiplié par le nombre des particules G. À ce produit sera donc aussi égal la dite somme des produits de chaque particule G par le carré de sa distance à la droite AE, ou bien le produit d'une seule particule G par la somme de tous ces carrés. Partant, lorsqu'on omet d'un côté et de l'autre la multiplication par la particule G, il est nécessaire que la dite somme des carrés soit égale au rectangle à côtés FA et LA multiplié par le nombre des particules dans lesquelles la figure ACB est divisée par hypothèse. C. Q. F. D. | |||||||||||||||||||||||||||||||||||
[pagina 269]
| |||||||||||||||||||||||||||||||||||
minimas aequales, atque à singulis ad rectam illam perpendiculares ductae: eruntGa naar margenoot+ omnium harum quadrata, simul sumpta, aequalia rectangulo cuidam, multiplici secundum ipsarum particularum numerum; quod nempe rectangulum fit à distantia centri gravitatis figurae ab eadem recta, & à subcentrica cunei, qui per illam super figura abscinditurGa naar voetnoot1).  [Fig. 82.]
Positis enim caeteris omnibus quae in constructione praecedenti, sit LA [Fig. 82] cunei ABD subcentrica in rectam EE. Oportet igitur ostendere, summam quadratorum omnium à distantiis particularum | figurae ACBGa naar margenoot+ aequari rectangulo ab FA, LA, multiplici secundum particularum numerum. Et constat quidem ex demonstratione praecedenti, altitudines parallelepipedorum singulorum, ut GK, aequales esse distantiis particularum, quae ipsorum bases sunt, ut G, ab recta AE. Quare, si jam parallelepipedum GK ducamus in distantiam GH, perinde est ac si particula G ducatur in quadratum distantiae GH. Eodemque modo se res habet in reliquis omnibus. Atqui producta omnia parallelepipedorum in distantias suas ab recta AE, aequantur simul producto ex cuneo ABD in distantiam LAGa naar margenoot*, quia cuneus gravitat super puncto L. Ergo etiam summa productorum à particulis singulis G, in quadrata suarum distantiarum ab recta AE, aequabitur producto ex cuneo ABD in rectam LA, hoc est, producto ex figura ACB in rectangulum ab FA, LA. Nam cuneus ABD, aequalis est producto ex figura ACB in rectam FAGa naar margenoot*. Rursus quia figura ACB aequalis est producto ex particula una G, in numerum ipsarum particularum; sequitur, dictum productum ex figura ACB in rectangulum FA, LA, aequari producto ex particula G in rectangulum ab FA, LA, multiplici secundum numerum particularum G. Cui proinde etiam aequalis erit dicta summa productorum, à particulis singulis G in quadrata suarum distantiarum ab recta AE, sive à particula una G in summam omnium horum quadratorum. Quare, omissa utrinque multiplicatione in particulam G, necesse est summam eandem quadratorum aequari rectangulo ab FA, LA, multiplici secundum numerum particularum in quas figura ACB divisa intelligitur. quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||
[pagina 270]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Proposition IX.Etant donnée une figure plane et dans le même plan une droite coupant la figure ou ne la coupant pas, sur laquelle sont abaissées des perpendiculaires de toutes les très petites particules égales dans lesquelles la figure est divisée par hypothèse, trouver la somme des carrés de toutes ces perpendiculaires, ou bien un plan qui, multiplié par le nombre des particules, soit égal à la dite somme des carrésGa naar voetnoot1).
Soit donnée [Fig. 83] la figure plane ABC et dans le même plan la droite ED, et la figure ayant été divisée par la pensée en de très petites particules égales, supposons abaissées sur la droite ED des perpendiculaires de toutes ces particules, comme l'est FK de la particule F. Qu'il faille trouver la somme des carrés de toutes ces perpendiculaires. Soit AL une tangente à la figure, parallèle à la droite donné ED et toute hors de la figure. Elle peut toucher la figure soit du même côté où est ED soit du côté opposé. Soit la droite GA, coupant ED en E, la distance du centre de gravité de la figure à la droite AL, et HA la subcentrique de l'onglet coupé sur la figure par un plan passant par la droite AL. Je dis que la somme cherchée des carrés est égale à la somme du rectangle AGH et du carré EG, multipliés par le nombre des particules dans lesquelles la figure est supposée divisée. En effet, puisse FK, prolongée s'il en est besoin, couper la tangente AL au point L. On peut alors en premier lieu, dans le cas où la droite ED est distante de la figure et que la tangente AL a été menée du même côté de la figure, démontrer la proposition comme suit. La somme de tous les FK2 est égale à un nombre égal de KL2 plus un nombre double de rectangles KLF plus autant de LF2. Mais la somme des KL2 est égale à celle des EA2. Et il est certain que l'ensemble des rectangles KLF est égal à autant de fois le rectangle EAG, puisque la somme des FL est égale à autant de fois la droite GAGa naar margenoot*). Enfin les LF2 sont égaux à un nombre égal de rectangles HAGGa naar margenoot†, | |||||||||||||||||||||||||||||||||||
[pagina 271]
| |||||||||||||||||||||||||||||||||||
Propositio IX.Ga naar margenoot+Datâ figurâ planâ & in eodem plano lineâ rectâ, quae vel secet figuram vel non, ad quam perpendiculares cadant à particulis singulis minimis & aequalibus, in quas figura divisa intelligitur; invenire summam quadratorum ab omnibus istis perpendicularibus; sive planum, cujus multiplex, secundum particularum numerum, dictae quadratorum summae oequale sitGa naar voetnoot1). 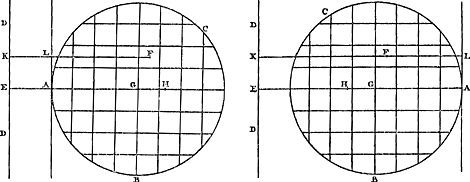 [Fig. 83.]
Sit data figura plana ABC [Fig. 83], & in eodem plano recta ED; divisâque figurâ cogitatu in particulas minimas aequales, intelligantur ab unaquaque earum perpendiculares ductae in rectam ED, sicut à particula F ducta est FK. Oporteatque invenire |Ga naar margenoot+ summam quadratorum ab omnibus istis perpendicularibus. Sit datae ED parallela recta AL, quae figuram tangat, ac tota extra eam posita sit. Potest autem figuram vel ab eadem parte ex qua est ED, vel à parte opposita contingere. Distantia vero centri gravitatis figurae ab recta AL sit recta GA, secans ED in E; & subcentrica cunei, super figura abscissi plano per rectam AL, sit HA. Dico summam quadratorum quaesitam aequari rectangulo AGH una cum quadrato EG, multiplicibus secundum particularum numerum, in quas figura divisa intelligitur. Occurrat enim FK, si opus est producta, tangenti AL in L puncto. Itaque primum, eo casu quo recta ED à figura distat, & tangens AL ad eandem figurae partem ducta est, sic propositum ostendetur. Summa omnium quadratorum FK aequatur totidem quadratis KL, una cum bis totidem rectangulis KLF, & totidem insuper quadratis LF. Sed quadrata KL aequantur totidem quadratis EA. Et rectangula KLF aequalia esse constat totidem rectangulis EAG, quia omnes FL aequales totidem GAGa naar margenoot*. Et denique quadrata LF aequantur totidem rectangulis HAGGa naar margenoot*, hoc est, totidem quadratis | |||||||||||||||||||||||||||||||||||
[pagina 272]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ en d'autres termes à autant de AG2 plus autant de rectangles AGH. Par conséquent l'ensemble des FK2 sera égal à un nombre égal de EA2 plus autant de fois le double du rectangle EAG plus autant de AG2 et de rectangles AGH. Mais trois de ces grandeurs, savoir EA2 + 2 EAG + AG2, constituent le carré EG2. Il appert donc que l'ensemble des KF2 est égal à un nombre égal de EG2 plus autant de fois le rectangle AGH. C. Q. F. D. Dans tous les autres cas, l'ensemble des carrés FK2 [Fig. 84] est égal à celui des KL2 moins deux fois le même nombre de rectangles KLF plus autant de fois LF2, en d'autres termes à un même nombre de EA2 moins autant de fois le double du rectangle EAG plus autant de AG2 et de rectangles AGH. Mais l'expression EA2 + AG2 - 2 EAG est toujours égale à EG2. Par conséquent dans ces cas aussi la somme des FK2 sera égale à celle des EG2 plus un nombre égal de rectangles AGH. La proposition est donc établie. Il s'ensuit que le rectangle AGH a la même grandeur, que AH soit la subcentrique de l'onglet limité par un plan passant par la première tangente parallèle à AL ou bien celle d'un onglet limité par un plan passant par la deuxième tangente. Par conséquent la longueur AG du premier cas est à AG du second cas, comme HG du second à HG du premier. Mais le rapport des droites AG entre elles est égal à celui des onglets limités dans l'un et l'autre cas par un plan passant par une des tangentes AL, comme cela résulte de la Prop. VII de la présente Partie. GH a donc aussi à GH un rapport inverse à celui des onglets correspondants. Il apparaît aussi que, le centre de gravité G de la figure plane étant donné ainsi que la subcentrique de l'onglet limité par un plan passant par l'une des deux tangentes parallèles AL, la subcentrique de l'onglet limité par un plan passant par l'autre tangente AL est également connue. | |||||||||||||||||||||||||||||||||||
Proposition X.Etant posées les mêmes choses que dans le cas de la proposition précédente, si la droite ED [Fig. 85] passe par G, centre de gravité de la figure ABC, la somme des | |||||||||||||||||||||||||||||||||||
[pagina 273]
| |||||||||||||||||||||||||||||||||||
AG cum totidem rectangulis AGH. Ergo quadrata omnia FK aequalia erunt totidemGa naar margenoot+ quadratis EA, cum totidem duplis rectangulis EAG, atque insuper totidem quadratis AG cum totidem rectangulis AGH. Atqui tria ista; nempe quadratum EA cum duplo rectangulo EAG & quadrato AG; faciunt quadratum EG. Ergo apparet quadrata omnia FK aequari totidem quadratis EG, una cum totidem rectangulis AGH. Quod erat ostendendum. 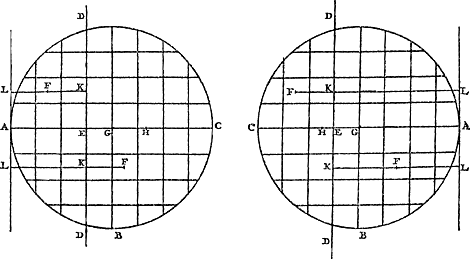 [Fig. 84.]
Porro in reliquis omnibus casibus, quadrata omnia FK [Fig. 84] aequantur totidem quadratis KL, minus bis totidem rectangulis KLF, plus totidem quadratis LF; hoc est, totidem quadratis EA, minus totidem duplis rectangulis EAG, plus totidem quadratis AG, cum toti|dem rectangulis AGH. Atqui, omnibus hisce casibus, fit quadratumGa naar margenoot+ EA, plus quadrato AG, minus duplo rectangulo EAG, aequale quadrato EG. Ergo rursus quadrato omnia FK aequalia erunt totidem quadratis EG, una cum totidem rectangulis AGH. Quare constat propositum. Hinc sequitur, rectangulum AGH eadem magnitudine esse, utriusvis cunei subcentrica fuerit AH; hoc est, sive per hanc, sive per illam tangentium parallelarum AL abscissi. Itaque AG unius casus ad AG alterius, ut HG hujus ad HG illius. Sicut autem rectae AG inter se, ita in utroque casu cunei per AL abscissi, ut colligitur ex prop. 7. huj. Ergo ita quoque reciproce GH ad GH. Apparet etiam, dato figurae planae centro gravitatis G, & subcentrica cunei, per alterutram tangentium parallelarum AL abscissi, dari quoque cunei, per tangentem alteram AL abscissi, subcentricam. | |||||||||||||||||||||||||||||||||||
[pagina 274]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ carrés des distances à la droite ED des particules dans lesquelles la figure est supposée divisée sera égale au seul rectangle AGH, multiplié par le nombre des particulesGa naar voetnoot1).
Ceci est évident, puisque dans ce cas le carré EG2 est nul. | |||||||||||||||||||||||||||||||||||
Proposition XI.Les mêmes choses étant derechef posées que dans le cas de l'avant-dernière proposition, DE [Fig. 86] étant un axe de symétrie de la figure plane ABC, VG la distance du centre de gravité de la demi-figure DAD à la droite ED, et GX la subcentrique de l'onglet coupé sur cette demi-figure par un plan passant par ED, le rectangle XGV sera égal au rectangle AGHGa naar voetnoot2).
En effet, le rectangle XGV, multiplié par le nombre des particules de la figure DAD, est égal à la somme des carrés des perpendiculaires abaissées sur la droite ED des particules de cette demi-figureGa naar margenoot*. Par conséquent le même rectangle XGV, multiplié par le nombre des particules de la figure entière ABC, sera égal à la somme des carrés des perpendiculaires abaissées sur la droite ED de toutes les particules de cette figure, c.à.d. au rectangle AGH multiplié par le même nombre de particules, comme cela résulte de la proposition précédente. D'où s'ensuit que les rectangles XGV et AGH sont égaux entre eux. C. Q. F. D. | |||||||||||||||||||||||||||||||||||
Proposition XII.Etant donnés dans un plan un nombre quelconque de points, si de leur centre de gravité on décrit un cercle de grandeur quelconque et qu'on tire à partir de tous les | |||||||||||||||||||||||||||||||||||
[pagina 275]
| |||||||||||||||||||||||||||||||||||
centrum gravitatis figurae ABC; erit summa quadratorum à distantiis particularum,Ga naar margenoot+ in quas figura | divisa intelligitur, ab recta ED, aequalis rectangulo soli AGH, multipliciGa naar margenoot+ secundum ipsarum particularum numerumGa naar voetnoot1).
Hoc enim manifestum est, quum nullum tunc sit quadratum EG. 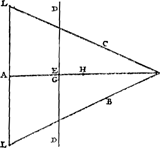 [Fig. 85.]
 [Fig. 86.]
| |||||||||||||||||||||||||||||||||||
Propositio XI.Positis rursus caeteris ut in praecedentium penultima; si DE [Fig. 86] sit axis figurae planae ABC, in duas aequales similesque portiones eam dividens, sitque insuper VG distantia centri gravitatis dimidiae figurae DAD ab recta ED, cuneivero, super ipsam abscissi per ipsam ED, subcentrica GX; erit rectangulum XGV aequale rectangulo AGHGa naar voetnoot2).
Est enim rectangulum XGV, multiplex secundum numerum particularum figurae DAD, aequale quadratis omnibus perpendicularium à particulis ejusdem figurae dimidiae in rectam ED cadentiumGa naar margenoot*. Ac proinde idem rectangulum XGV, multiplex secundum numerum particularum totius figurae ABC, aequale erit quadratis perpendicularium, abomnibus particulis figurae hujus in rectam ED demissarum; hoc est, rectangulo AGH multiplici secundum eundem particularum numerum, ut constat ex propos. praecedenti. Unde sequitur rectangula XGV, AGH inter se aequalia esse. quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||
[pagina 276]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ points donnés à un point quelconque situé sur la circonférence de ce cercle des lignes droites, la somme des carrés de toutes ces droites sera toujours égale à un même planGa naar voetnoot1).
Soient A B C D [Fig. 87] les points donnés, et E leur centre de gravité ou bien celui de grandeurs égales suspendues à eux. Qu'un cercle de grandeur quelconque Ff soit décrit du centre E, et un point quelconque tel que F étant pris sur sa circonférence, qu'on le relie par les droites AF, BF, CF, DF aux points donnés. Je dis que l'ensemble des carrés de toutes ces droites est égal à un certain plan, toujours le même, où que le point F soit placé sur la circonférence. En effet, soient tirées les droites GH, GK formant un angle droit et pour chacune desquelles les points donnés soient situés d'un même côté. Abaissons sur ces deux droites de chacun des points donnés les perpendiculaires AL, AK; BM, BO; CN, CP; DH, DQ; et sur l'une quelconque d'elles GH ou GK, les perpendiculaires ER, FS provenant du centre de gravité E et du point F. Ensuite aussi les perpendiculaires AV, BX, CY, DZ des points donnés sur FS; et soit FT une perpendiculaire sur ER. Soit maintenant
Or, comme E est le centre de gravité des points A, B, C, D, si l'on prend la somme des perpendiculaires AL, BM, CN, DH et qu'on là divise en autant de parties qu'il y a de points donnés, ER sera égale à une de ces partiesGa naar margenoot*. De même, la somme des perpendiculaires AK, BO, CP, DQ ayant été divisée en autant de parties, la perpendiculaire tirée de E sur la droite GK, ou bien la droite RG, sera égale à l'une d'ellesGa naar margenoot*. Par conséquent, si la somme de toutes les perpendiculaires AL, BM, CN, DH ou a + b + c + d est appelée l, m celle de AK, BO, CP, DQ ou e + f + g + h et θ le nombre des points donnés, on aura ER = l/θ et RG = m/θ. | |||||||||||||||||||||||||||||||||||
[pagina 277]
| |||||||||||||||||||||||||||||||||||
illius | circumferentia lineae rectae; erit summa quadratorum ab omnibus semperGa naar margenoot+ eidem plano aequalisGa naar voetnoot1).Ga naar margenoot+ 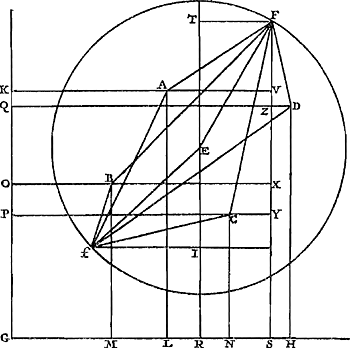 [Fig. 87.]
Sint data puncta ABCD [Fig. 87]: centrumque gravitatis eorum, sive magnitudinum aequalium ab ipsis suspensarum, sit E; & centro E describatur circulus quilibet Ff, in cujus circumferentia sumpto puncto aliquo, ut F, ducanturadid, à datis punctis, rectae AF, BF, CF, DF. Dico earum omnium quadrata, simulsumpta, aequalia esse plano cuidam dato, semperque eidem, ubicunque in circumferentia punctum F sumptum fuerit. Ducantur enim rectae GH, GK, angulum rectum constituentes, & quarum unicuique omnia data puncta sint posita ad eandem partem. Et à singulis in utramque harum perpendiculares agantur AL, AK; BM, BO; CN, CP; DH, DQ. A centro autem gravitatis E, & à puncto F, in alterutram duarum, GH vel GK, perpendiculares ER, FS. Et item, à datis punctis, in ipsam FS perpendiculares AV, BX, CY, DZ. Et FT perpendicularis in ipsam ER. Porro sit jam
Quia autem E est centrum gravitatis punctorum A, B, C, D; si addantur in unum perpendiculares AL, BM, CN, DH, compositaque ex omnibus dividatur in tot partes, quot sunt data puncta; earum partium uni aequalis erit ERGa naar margenoot*. Similiterque, divisâ in toti|dem partes summâ perpendicularium AK, BO, CP, DQ, earum uni aequalisGa naar margenoot+ erit perpendicularis, ducta ex E in rectam GK, sive ipsa RGGa naar margenoot*. Itaque, si summa omnium AL, BM, CN, DH, sive a + b + c + d vocetur l: summa vero omnium, AK, BO, CP, DQ, sive e + f + g + h, vocetur m: & numerus, datorum punctorum multitudinem exprimens, dicatur θ, erit ER ∞ l/θ; & RG ∞ m/θ. Cumque GS sit x, | |||||||||||||||||||||||||||||||||||
[pagina 278]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Et comme GS = x, on aura RS ou 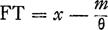 ou bien m/θ - x si GR > GS; dans l'un et l'autre cas ou bien m/θ - x si GR > GS; dans l'un et l'autre cas 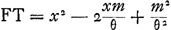 . Cette quantité étant soustraite de FE2 ou z2, il restera le carré de . Cette quantité étant soustraite de FE2 ou z2, il restera le carré de 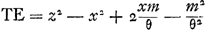 . Et par conséquent . Et par conséquent 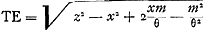 . Or, nous avions ER = l/θ. Par conséquent . Or, nous avions ER = l/θ. Par conséquent 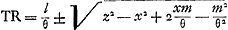 . Appelons cette longueur TRy pour être courts. Formons maintenant la somme de tous les carrés de FA, FB, FC, . Appelons cette longueur TRy pour être courts. Formons maintenant la somme de tous les carrés de FA, FB, FC, 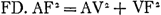 . Or, AV est la différence de VK et de AK ou de SG et de AK; par conséquent . Or, AV est la différence de VK et de AK ou de SG et de AK; par conséquent 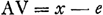 ou e - x et ou e - x et 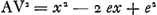 . Mais VF est égale à la différence de FS et de VS ou de FS et de AL; par conséquent . Mais VF est égale à la différence de FS et de VS ou de FS et de AL; par conséquent 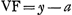 ou a - y, et ou a - y, et 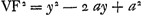 . Prenant la somme de AV2 et de VF2 on obtient . Prenant la somme de AV2 et de VF2 on obtient 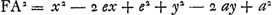 . On trouvera de la même manière les carrés des autres droites FB, FC, FD. Tout étant disposé par ordre on aura ceci: . On trouvera de la même manière les carrés des autres droites FB, FC, FD. Tout étant disposé par ordre on aura ceci:
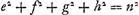 et et 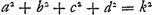 , sera θx2 - 2 mx + n2 + θy2 - 2 ly + k2, puisque θ était le nombre des points donnés, donc aussi le nombre des carrés, et que nous avions posé , sera θx2 - 2 mx + n2 + θy2 - 2 ly + k2, puisque θ était le nombre des points donnés, donc aussi le nombre des carrés, et que nous avions posé 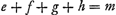 et et 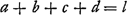 . .
Or, si dans cette somme, savoir dans les termes 2 θy et 2 ly, on substitue à y l'expression qui fut désignée par cette lettre, c.à.d. 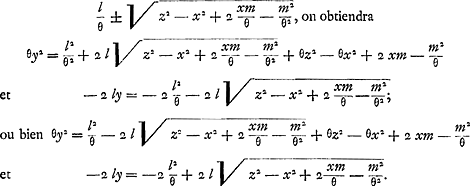 | |||||||||||||||||||||||||||||||||||
[pagina 279]
| |||||||||||||||||||||||||||||||||||
erit RS sive FT ∞ x - m/θ; vel m/θ - x, si GR major quam GS; & semper quadratumGa naar margenoot+ 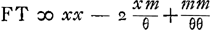 . quo ablato ab quadrato FE ∞ zz, relinquetur quadratum . quo ablato ab quadrato FE ∞ zz, relinquetur quadratum 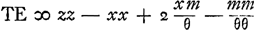 . Et proinde . Et proinde 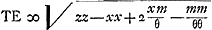 . Erat autem ER ∞ l/θ. Itaque . Erat autem ER ∞ l/θ. Itaque 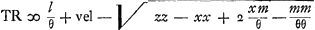 . quae TR, brevitatis gratia, dicatur y. Colligamus jam porro summam quadratorum omnium FA, FB, FC, FD. Quadratum AF aequatur quadratis AV, VF. Est autem AV aequalis differentiae duarum VK, AK, sive duarum SG, AK; ac proinde AV ∞ x - e vel e - x; & qu. AV ∞ xx - 2 ex + ee. VF vero aequalis est differentiae duarum FS, VS sive duarum FS, AL; ac proinde VF ∞ y - a vel a - y; & qu. VF ∞ yy - 2 ay + aa. Additisque quadratis AV, VF, sit quadratum FA ∞ xx - 2ex + ee + yy - 2ay + aa. Eodemque modo invenientur quadrata reliquarum FB, FC, FD; atque omnia ordine disposita erunt haec; . quae TR, brevitatis gratia, dicatur y. Colligamus jam porro summam quadratorum omnium FA, FB, FC, FD. Quadratum AF aequatur quadratis AV, VF. Est autem AV aequalis differentiae duarum VK, AK, sive duarum SG, AK; ac proinde AV ∞ x - e vel e - x; & qu. AV ∞ xx - 2 ex + ee. VF vero aequalis est differentiae duarum FS, VS sive duarum FS, AL; ac proinde VF ∞ y - a vel a - y; & qu. VF ∞ yy - 2 ay + aa. Additisque quadratis AV, VF, sit quadratum FA ∞ xx - 2ex + ee + yy - 2ay + aa. Eodemque modo invenientur quadrata reliquarum FB, FC, FD; atque omnia ordine disposita erunt haec;
Horum vero summa, si ponamus quadrata ee + ff + gg + hh ∞ nn; & quadrata aa + bb + cc + dd ∞ kk; erit ista, θxx - 2mx + nn + θyy - 2ly + kk. Siquidem θ erat numerus datorum punctorum ideoque & quadratorum, positumque fuerat e + f + g + h ∞ m, & a + b + c + d ∞ l. In ista vero summa, si in terminis θyy & 2ly, pro y, ponatur id cujus loco positum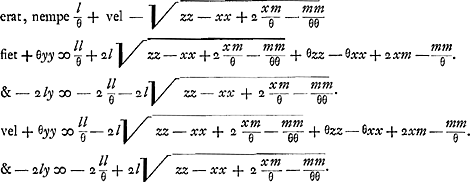
| |||||||||||||||||||||||||||||||||||
[pagina 280]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Par conséquent dans l'un et l'autre cas on aura pour
θy2 - 2 ly: - l2/θ + θz2 - θx2 + 2 xm - m2/θ. En y ajoutant les autres quantités comprises dans la somme susdite, θx2 - 2 xm + n2 + k2, la somme totale, qui est celle des carrés de FA, FB, FC, FD, deviendra égale à 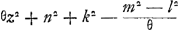 . Ce qui est apparemment un plan déterminé puisque toutes ces quantités sont connues; il est donc manifeste qu'on trouve toujours la même valeur où que le point F soit pris sur la circonférence. C. Q. F. D. . Ce qui est apparemment un plan déterminé puisque toutes ces quantités sont connues; il est donc manifeste qu'on trouve toujours la même valeur où que le point F soit pris sur la circonférence. C. Q. F. D.
Que si les points donnés ont par hypothèse des poids divers, commensurables entre eux, comme lorsque le point A pèse 2, B 3, C 4 et D 7; qu'après avoir trouvé leur centre de gravité on décrit de nouveau un cercle, à un point de la circonférence duquel on relie les points donnés par des lignes droites; et qu'on multiplie le carré de chacune de ces droites par le nombre qui exprime le poids du point correspondant, de sorte qu'on prend deux fois le carré de AF, trois fois celui de BF, quatre fois celui de CF et sept fois celui de DF; je dis qu'alors aussi la somme totale sera égale à un espace donné, toujours le même, où que le point ait été pris sur la circonférence. Ceci ressort de la démonstration précédente, si nous nous figurons les points comme multiples selon les nombres de la pesanteur attribuée à chacun d'eux, comme s'il y avait en A deux points réunis, en B trois, en C quatre, en D sept tous également pesants. | |||||||||||||||||||||||||||||||||||
Proposition XIII.Lorsu'une figure plane ou une ligne qui est dans un plan est suspendue diversement de points pris dans ce plan et également distants de son centre de gravité, cette figure ou ligne est isochrone à elle-même dans le cas où son oscillation est latéraleGa naar voetnoot1).
Soit [Fig. 88] une figure plane, ou une ligne située dans le plan ABC, dont D désigne le centre de gravité. Décrivons de ce centre dans le même plan une circonférence de cercle ECF. Je dis que si une figure suspendue en un point quelconque de cette circonférence tel que E, C ou G, oscille latéralement, elle est isochrone avec elle-même ou avec un même pendule simple. Soit en premier lieu la figure suspendue au point E. Lorsque celui-ci est situé en dehors de la figure, comme ici, il faut se figurer la ligne EH à laquelle la figure est suspendue rigide et attachée à elle immuablement. Supposons la figure ABC divisée en de très petites particules égales, des centres de gravité de toutes lesquelles il faut tirer des droites au point E; il est manifeste que | |||||||||||||||||||||||||||||||||||
[pagina 281]
| |||||||||||||||||||||||||||||||||||
Ac proinde, utroque casu, pro θyy - 2ly habebitur - ll-/θ + θzz-θxx + 2xm - mm/θ.Ga naar margenoot+ Quò appositis reliquis quantitatibus, summa praedi|cta contentis, θxx - 2xm + nn + kk,Ga naar margenoot+ fiet tota summa, nempe quadratorum FA, FB, FC, FD, 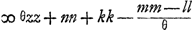 . Quod apparet esse planum datum, cum hae quantitates omnes datae sint; semperque idem reperiri, ubicunque in circumferentia sumptum fuerit punctum F. quod erat demonstrandum. . Quod apparet esse planum datum, cum hae quantitates omnes datae sint; semperque idem reperiri, ubicunque in circumferentia sumptum fuerit punctum F. quod erat demonstrandum.
Quod si puncta data diversas gravitates habere ponantur, invicem commensurabiles, ut si punctum A ponderet ut 2, B ut 3, C ut 4, D ut 7, eorumque reperto gravitatis centro, circulus rursus describatur, ad cujus circumferentiae punctum, à datis punctis rectae ducantur, ac singularum quadrata multiplicia sumantur secundum numerum ponderis puncti sui; ut quadratum AF duplum, BF triplum, CF quadruplum, DF septuplum; dico rursus summam omnium aequalem fore spatio dato, semperque eidem, ubicunque in circumferentia punctum fuerit. Patet enim hoc ex praecedenti demonstratione, si imaginemur puncta ipsa multiplicia secundum numeros attributae cuique gravitatis; quasi nempe in A duo puncta conjuncta sint, in B tria, in C quatuor, in D septem, atque illa omnia aequaliter gravia. | |||||||||||||||||||||||||||||||||||
Propositio XIII.Si figura plana, vel linea in plano existens, aliter atque aliter suspendatur à punctis, quae, in eodem plano accepta, aequaliter à centro gravitatis suae distent; agitata motu in latus, sibi ipsi isochrona estGa naar voetnoot1). 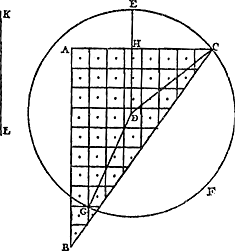 [Fig. 88]
Sit [Fig. 88] figura plana, vel linea in plano existens ABC, cujus centrum gravitatis D. quo eodem centro, circumferentia circuli in eodem plano describatur, ECF. Dico, si à quovis in illa puncto, ut E, C, vel G, suspensa figura agitetur in latus; sibiipsi, sive eidem pendulo simplici, isochronam esse. Sit prima suspensio ex E puncto, quando autem est extra figuram, ut hic, putandum est lineam EH, ex qua figura pendet, rigidam esse, atque immobiliter ipsi affixam. Intelligatur figura ABC divisa in particulas minimas aequales, à quarum omnium centris gravitatis, ad punctum E, rectae ductae sint; quas quidem manifestum est, | |||||||||||||||||||||||||||||||||||
[pagina 282]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ lorsque la figure oscille latéralement toutes ces droites sont perpendiculaires à l'axe d'oscillation. Par conséquent la somme des carrés de toutes ces perpendiculaires, divisée par la droite ED multipliée par le nombre des particules dans lesquelles la figure est divisée, constitue la longueur KL du pendule simple isochrone avec la figureGa naar margenoot*. Mais lorsque la figure est suspendue au point G, la longueur du pendule simple isochrone est de nouveau trouvée en divisant la somme des carrés des lignes qui relient les particules de la figure au point G par la droite GD multipliée par le nombre des particulesGa naar margenoot*. Or, comme les points G et E se trouvent sur une circonférence décrite du centre D, c.à.d. du centre de gravité de la figure ABC ou, si l'on veut, de celui de tous les centres des particules égales de la figure, la somme des carrés des lignes qui relient les dites particules au point G, sera égale à la somme des carrés des lignes tirées des mêmes particules au point EGa naar margenoot*. Mais ces sommes de carrés sont, dans l'une et l'autre suspension, appliquées à des grandeurs égales, savoir, dans le cas de la suspension au point E, à la droite ED multipliée par le nombre de toutes les particules, et dans celui de la suspension du point G, à la droite DG multipliée par le même nombre de particules. Il est donc évident que par cette dernière division, savoir lorsque la suspension est en G, la longueur du pendule isochrone devient la même que dans le cas de la première suspension, c.à.d. KL. On démontrera de la même manière l'isochronisme avec le pendule KL lorsque la figure est suspendue en C ou en un autre point quelconque de la circonférence ECF. La proposition est donc établie. | |||||||||||||||||||||||||||||||||||
Proposition XIV.Etant donnée une figure solide et une ligne droite de longueur indéterminée qui tombe en dehors de la figure ou bien qui la coupe, et la figure ayant été divisée par la pensée en de très petites particules égales, à partir de chacune desquelles on suppose des perpendiculaires abaissées sur la dite droite, trouver la somme de tous leurs carrés, en d'autres termes trouver un plan dont la multiplication par le nombre des particules donne un produit égal à la dite somme des carrésGa naar voetnoot1).
Soit donnée [Fig. 89] la figure solide ABCD et une ligne droite passant par le point E et supposée perpendiculaire au plan de cette page; cette ligne peut couper la figure ou tomber en entier hors d'elle. Étant supposé qu'à partir de chacune des très petites particules égales qui constituent le solide ABCD, telles que F, soit tirée une perpendiculaire sur la droite donnée E, telle que FE, il faut maintenant trouver la somme de tous les FE2. Coupons la figure par le plan EAC passant par la dite ligne donnée et par le centre de gravité de la figure. Figurons-nous aussi un deuxième plan passant par la même ligne donnée et par EG qui lui est perpendiculaire. On sait que le carré de chaque perpendiculaire abaissée d'une des dites particules sur la ligne donnée passant par E, telle que FE, est égal à la somme des carrés des | |||||||||||||||||||||||||||||||||||
[pagina 283]
| |||||||||||||||||||||||||||||||||||
quum moveatur figura motu in latus, esse ad axem agitationis perpendiculares. HarumGa naar margenoot+ igitur omnium perpendicularium quadrata, divisa per rectam ED, multiplicem secundum numerum particularum in quas figura divisa est, efficiunt longitudinem penduli simplicis, figurae isochroniGa naar margenoot*, | quae sit KL. Suspensâ autem figurâ ex punctoGa naar margenoot+ G, rursus longitudo penduli simplicis isochroni invenitur, dividendo quadrata omnia linearum, quae à particulis figurae ducuntur ad punctum G, per rectam GD, multiplicem secundum earundem particularum numerumGa naar margenoot*. Quum igitur puncta G & E sint in circumferentia descripta centro D, quod est centrum gravitatis figurae ABC, sive centrum gravitatis punctorum omnium, quae centra sunt particularum figurae aequalium; erit proinde summa quadratorum à lineis, quae à dictis particulis ad punctum G ducuntur, aequalis summae quadratorum à lineis quae ab iisdem particulis ducuntur ad punctum EGa naar margenoot*. Hae vero quadratorum summae, utraque suspensione, applicantur ad magnitudines aequales: quippe, in suspensione ex E, ad rectam ED, multiplicem secundum numerum omnium particularum; in suspensione autem ex G, ad rectam DG, multiplicem secundum earundem particularum numerum. Ergo patet, ex applicatione hac posteriori, quum nempe suspensio est ex G, fieri longitudinem penduli isochroni eandem atque ex applicatione priori, hoc est, eandem ipsi KL. Eodem modo, si ex C, vel alio quovis puncto circumferentiae ECF, figura suspendatur, eidem pendulo KL isochrona esse probabitur. Itaque constat propositum. | |||||||||||||||||||||||||||||||||||
Propositio XIV.Datâ figurâ solidâ, & lineâ rectâ interminatâ, quae vel extra figuram cadat, vel per eam transeat; divisâque | figurâ cogitatu in particulas minimas aequales, àGa naar margenoot+ quibus omnibus ad datam rectam perpendiculares ductae intelligantur; invenire summam omnium quae ab ipsis fiunt quadratorum, sive planum, cujus multiplex secundum particularum numerum, dictae quadratorum summae aequale sitGa naar voetnoot1).
Sit data [Fig. 89] figura solida ABCD, & linea recta quae, per punctum E transiens, ad planum hujus paginae erecta intelligatur: quaeque vel secet figuram, vel tota extra cadat. Intellectoque, à singulis particulis minimis aequalibus, solidum ABCD constituentibus, velut F, rectas duci perpendiculares in datam rectam per E, quemadmodum hic FE, oporteat omnium quadratorum FE summam invenire. Secetur figura plano EAC, per dictam datam lineam & per centrum gravitatis figurae ducto. Item aliud planum intelligatur per eandem lineam datam, perque EG, quae ipsi est ad angulos rectos. Constat jam, quadratum rectae cujusque, quae à particula di|ctarum aliqua, ad lineamGa naar margenoot+ datam per E perpendicularis ducitur, sicut FE, aequari quadratis duarum FG, FH, | |||||||||||||||||||||||||||||||||||
[pagina 284]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ deux lignes FG et FH partant de la même particule et perpendiculaires respectivement aux plans mentionnés passant par EG et ECGa naar margenoot*. Par conséquent, si nous pouvons apprendre à connaître la somme des carrés de toutes les perpendiculaires menées des particules aux dits plans passant par EG et EC, nous aurons aussi, égale à l'ensemble de ces deux sommes, celle des carrés des perpendiculaires menées de toutes ces particules à la droite donnée passant par le point E. Or, la première de ces deux sommes de carrés sera calculée comme suit. Considérons d'abord la figure plane OQP placée à côté de la figure solide ABCD, de la même hauteur qu'elle, et ainsi construite que lorsqu'on la coupe par les droites QQ, RR, correspondant aux plans MM, NN qui coupent la figure solide ABCD et parallèles à ces plans, le rapport de ces droites entre elles soit le même que celui de ces plans, bien entendu si l'on prend de part et d'autre les droites et les plans qui se correspondent. La ligne RR p.e. est à QQ, comme le plan NN à MM. Si l'on suppose donc la figure plane OQP divisée en autant de très petites particules égales qu'il y en a dans le solide ABCD, il y aura aussi dans chaque segment tel que QQRR de la figure plane un aussi grand nombre de particules qu'il y en a dans le segment correspondant MMNN de la figure solide; partant la somme des carrés des perpendiculaires abaissées de toutes les particules de la figure OQP sur le plan EG sera égal à la somme des carrés des perpendiculaires abaissées sur le même plan EG de toutes les particules de la figure solide. Mais cette première somme de carrés sera connue, lorsque sera donné dans la figure OQL et son onglet ce que nous avons dit dans la Prop. IX de | |||||||||||||||||||||||||||||||||||
[pagina 285]
| |||||||||||||||||||||||||||||||||||
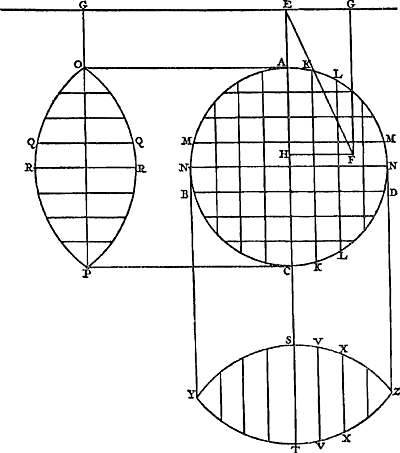 [Fig. 89.]Ga naar margenoot+
quae, ab eadem particula, in plana per EG & EC ante dicta, perpendiculares agunturGa naar margenoot*. Quare, si cognoscere possimus summam quadratorum, quae à particulis universis cadunt in plana dicta per EG & EC; habebimus etiam huic aequalem summam quadratorum à perpendicularibus, quae ab universis iisdem particulis cadunt in rectam datam per E punctum. Illa vero prior quadratorum summa colligetur hoc modo. Ponatur primò figuram planam dari OQP, ad latus figurae solidae ABCD, ejusdem cum ipsa altitudinis, quaeque sit ejusmodi, ut secta lineis rectis QQ, RR, quae respondeant planis figuram solidam ABCD secantibus MM, NN, & his parallelis; eadem sit dictarum linearum inter se, quae & planorum horum ratio, si nempe sumantur utrinque quae in ordine sibi respondent. Ut si linea RR sit ad QQ quemadmodum planum NN ad MM. Quod si igitur figura plana OQP, in totidem particulas minimas aequales divisa intelligatur, quot intelliguntur in solido ABCD, erunt etiam in unoquoque segmento figurae planae, velut QQRR, tot numero particulae, quot sunt in figurae solidae segmento MM NN, isti segmento respondente; ac proinde & summa quadratorum, à perpendicularibus omnium particularum figurae OQP in planum EG; aequabitur summae quadratorum, à perpendicularibus omnium particularum figurae solidae, in idem planum EG productis. Illa autem quadratorum summa data erit, si dentur in figura OQP, cuneoque | |||||||||||||||||||||||||||||||||||
[pagina 286]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ la présente Partie être requis à ce but. Ces choses étant données, la somme des carrés des perpendiculaires abaissées sur le plan EG de toutes les particules du solide ABCD sera donc aussi connue. Considérons maintenant une deuxième figure plane SYTZ de même largeur que le solide ABCD, c.à.d. comprise entre les plans tangents BY, DZ du solide, parallèle au plan EAC et ainsi construite que lorsqu'elle est coupée par les lignes droites VV, XX, etc. correspondant aux plans KK, LL, etc. qui coupent la figure ABCD et parallèles à ces plans, les rapports de ces lignes et des plans correspondants soient égaux. Derechef la somme des carrés des perpendiculaires abaissées des particules de la figure SYTZ sur la droite ST sera égale à celle des carrés de toutes les perpendiculaires abaissées sur le plan AC des particules du solide ABCD. Mais la somme des premiers carrés sera donnée lorsque la distance du centre de gravité de la figure STYZ de la droite BY ou DZ est connue ainsi que la distance à une de ces mêmes droites du centre de gravité de l'onglet correspondant limité par un plan passant par la même droiteGa naar margenoot*. Ou bien, si la figure SYTZ a une forme symétrique et que ST représente son axe, la même somme des carrés sera donnée si l'on connaît la distance à l'axe ST du centre de gravité de la demi-figure SZT ainsi que la distance à cet axe du centre de gravité de l'onglet coupé sur la même demi-figure par un plan passant par l'axeGa naar margenoot*. Par conséquent, ceci étant donné, on connaîtra aussi la somme des carrés des perpendiculaires abaissées par hypothèse sur le plan EAC de toutes les particules du solide ABCD. Mais nous avons trouvé auparavant la somme des carrés de toutes les | |||||||||||||||||||||||||||||||||||
[pagina 287]
| |||||||||||||||||||||||||||||||||||
 [Fig. 89.]Ga naar margenoot+
illius, quae propos. 9. huj. requiri diximus. Ergo his datis, dabitur quoque summa quadratorum, à perpendicularibus quae, à particulis omnibus solidi ABCD, ducuntur in planum EG. Ponatur nunc alia item figura plana SYTZ, ejusdem cum solido ABCD latitudinis, hoc est, quam includant plana BY, DZ solidum contingentia, ac parallela plano EAC, quaeque sit ejusmodi, ut, secta lineis rectis VV, XX &c. quae respondeant planis figuram ABCD secantibus, KK, LL, & his parallelis, faciat eandem inter se rationem linearum harum atque illorum planorum, si sumantur quae sibi mutuo respondent. Itaque rursus quadrata simul omnia perpendicularium, à particulis figurae SYTZ in rectam ST cadentium, aequalia erunt quadratis omnibus perpendicularium quae, à particulis solidi ABCD, ducuntur in planum AC. Illorum autem summa quadratorum data erit, si detur distantia centri gravitatis figurae SYTZ ab recta BY vel DZ; nec non distantia indidem centri gravitatis cunei sui abscissi plano per eandem rectamGa naar margenoot*. Vel, figura SYTZ ordinata existente, ut ST sit axis ejus, eadem quadratorum summa dabitur, si detur distantia centri gravitatis figurae dimidiae SZT ab axe ST, item centri gra|vitatis cunei, super eadem dimidia figura, abscissiGa naar margenoot+ plano per axem ductoGa naar margenoot*. Ergo, his datis, dabitur quoque summa quadratorum à perpendicularibus quae, à particulis omnibus solidi ABCD, ductae intelliguntur in planum | |||||||||||||||||||||||||||||||||||
[pagina 288]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ perpendiculaires abaissées sur le plan EG. Nous connaîtrons donc aussi l'ensemble de ces deux sommes, c.à.d. d'après ce qui a été démontré plus haut, la somme des carrés des perpendiculaires abaissées de toutes les particules du solide ABCD sur la ligne droite passant par E et perpendiculaire au plan de cette page. C'est ce qu'il fallait faire. | |||||||||||||||||||||||||||||||||||
Proposition XV.Les mêmes choses étant posées, si le solide ABCD est de telle nature que la figure plane SYTZ [Fig. 89] qui lui est proportionnelle, n'a pas une distance connue de son centre de gravité aux tangentes BY ou DZ, ou bien que la subcentrique de l'onglet coupé sur elle par un plan passant par ces mêmes droites BY ou DZ est inconnue, mais que dans la figure OQP placée à côté d'elle la distance Φ P [Fig. 90] du centre de gravité de la demi-figure OPV à l'axe OP est donnée; il sera possible en partant de là de trouver la somme des carrés des distances des particules du solide ABCD au plan EC. Mais il faut que toutes les sections NN, MM soient des plans semblables et que le plan EC passe par les centres de gravité d'eux tous; il en est ainsi dans le cas du prisme, de la pyramide, du cône, des conoïdes et de beaucoup d'autres figures. Il est encore nécessaire que l'on connaisse les distances du centre de gravité de ces plans à des tangentes parallèles à l'axe d'oscillation ainsi que les subcentriques des onglets coupés sur eux par des plans passant par les mêmes tangentesGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
[pagina 289]
| |||||||||||||||||||||||||||||||||||
EAC. Invenimus autem & summam quadratorum, à perpendicularibus omnibus inGa naar margenoot+ planum per EG ductis. Ergo & aggregatum utriusque summae habebitur, hoc est, per superius ostensa, summa quadratorum perpendicularium quae, à particulis omnibus solidi ABCD, cadunt in rectam datam per E transeuntem, & ad paginae hujus planum erectam. quod erat faciendum. | |||||||||||||||||||||||||||||||||||
Propositio XV.Iisdem positis, si solidum ABCD [Fig. 89] sit ejusmodi, ut figura plana SYTZ. ipsi proportionalis, non habeat notam distantiam centri gravitatis à tangentibus BY vel DZ, vel, ut subcentrica cunei super ipsa abscissi, plano per easdem BY vel DZ, ignoretur; in figura tamen proportionali, quae à latere est, OQP, detur distantia ΦP [Fig. 90], qua centrum gravitatis figurae dimidiae OPV abest ab axe OP; licebit hinc invenire summam quadratorum à distantiis particularum solidi ABCD à plano EC. Oportet autem ut sectiones omnes, NN, MM, sint plana similia; utque per omnium centra gravitatis trsnseat planum EC; quemadmodum in prismate, pyramide, cono, conoidibus, multisque aliis figuris contingit. Atque eorum planorum distantias centri gravitatis, super tangentibus axi oscillationis parallelis, datas esse necesse est; uti & subcentricas cuneorum, qui super ipsis abscinduntur, ductis planis per easdem tangentesGa naar voetnoot1). 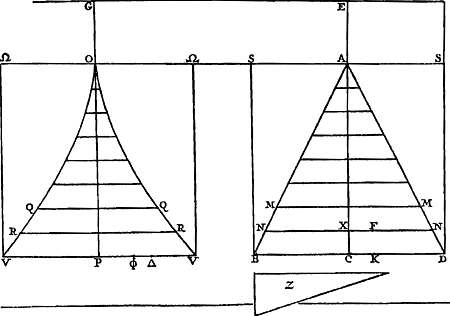 [Fig. 90.]
| |||||||||||||||||||||||||||||||||||
[pagina 290]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Par exemple, si BD [Fig. 90] est la plus grande des dites sections, et qu'on considère en B une droite parallèle à l'axe E, c.à.d. perpendiculaire au plan qu'on voit ici, il faut que l'on connaisse la distance BD du centre de gravité de la section à la dite ligne en B, laquelle soit BC; et de même la subcentrique de l'onglet coupé sur la section BD par le plan passant par la même ligne en B, laquelle subcentrique soit BK. Car, ces choses étant données et PV étant divisée en deux parties égales en ∆, si l'on fàit que comme ∆ P est à P Φ, ainsi soit le rectangle BCK à un certain espace Z; je dis que celui-ci, multiplié par le nombre des particules du solide ABCD, est égal à la somme cherchée des carrés des distances des mêmes particules au plan EC. En effet, il est certain que la somme des carrés des distances des particules de la section plane BD au plan EC passant par son centre de gravité, ou bien celle des carrés des distances au même plan des particules solides du segment BNND, est égale au rectangle BCK multiplié par le nombre des dites particulesGa naar margenoot*. Pareillement, si NX est la distance du centre de gravité de la section plane NN à la droite que nous supposons passer par N parallèlement à l'axe E, et que NF représente la subcentrique de l'onglet coupé sur cette section par un plan passant par la même droite; les carrés des distances au plan EC des particules planes de la section NN, ou bien les carrés des distances au même plan des particules solides du segment NMMN, seront égaux au rectangle NXF multiplié par le nombre des particules de la section NN ou du segment NMMN. Or, BD est divisée en C et K, de la même manière que NN l'est en X et F. Par conséquent le rectangle BCK est au rectangle NXF comme BD2 est à NN2. Nous savons que le nombre des particules de la section BD est à celui des particules de la section NN comme ces sections sont entre elles, c.à.d. comme BD2 est à NN2. Par conséquent le rectangle BCK, multiplié par le nombre des particules de la section BD, est au rectangle NXF multiplié par le nombre des particules de la section NN, comme BD4 est à NN4, en d'autres termes, comme VV2 est à RR2 dans la figure proportionnelle. Par conséquent la première somme des carrés des distances des particules du segment BNND au plan EC est à la deuxième somme des carrés des distances des particules du segment NMMN comme VV2 est à RR2. Et l'on démontrera de la même manière que les sommes des carrés des distances des particules dans les autres segments du solide ABCD sont entre elles dans le rapport des carrés des droites de la figure OVV qui correspondent à la base de chaque segment. C'est pourquoi la somme des carrés des distances au plan EC des particules de tous les segments du solide ABCD sera à la somme des carrés des distances des particules d'un nombre égal de segments égaux au plus grand segment, c.à.d. des segments du cylindre ou prisme BDSS, ayant la même base et la même hauteur que le solide ABCD, comme la somme des carrés des droites VV, RR, QQ, etc. est à un nombre égal de carrés de droites toutes égales à la plus grande VV, c.à.d. comme le solide OVV de révolution autour de l'axe OP est au cylindre VVΩΩ ayant la même base et la même hauteur. Or, il est clair que ce rapport du solide OVV au cylindre VVΩΩ se compose | |||||||||||||||||||||||||||||||||||
[pagina 291]
| |||||||||||||||||||||||||||||||||||
Veluti, si maxima dictarum sectionum sit BD, & in B intelligatur recta parallela axiGa naar margenoot+ E, hoc est, erecta ad planum quod hic conspicitur, oportet datam esse distantiam centri gr. sectionis BD à dicta linea in B, quae sit BC, itemque subcentricam cunei, super sectione BD abscissi, plano ducto per eandem lineam in B, quae subcentrica sit BK. Etenim his datis, divisâque PV bisariam in ∆, si fiat sicut ∆P ad | PΦ, ita rectangulumGa naar margenoot+ BCK ad spatium quoddam Z; dico hoc ipsum, multiplex per numerum particularum solidi ABCD, aequari summae quaesitae quadratorum, à distantiis earundem particularum à plano EC. Quadrata enim à distantiis particularum planae sectionis BD, à plano EC, quod per centrum gravitatis suae transit; sive quadrata à distantiis particularum solidarum segmenti BNND à plano eodem, aequari constat rectangulo BCK, multiplici per numerum dictarum particularumGa naar margenoot*. Similiter, si planae sectionis NN distantia centri gravitatis, ab recta quae in N intelligitur axi E parallela, sit NX; subcentrica vero cunei super ipsa abscissi, plano per eandem rectam, sit NF; erunt quadrata à distantiis particularum planarum sectionis NN à plano EC, sive quadrata à distantiis particularum solidarum segmenti NMMN, à plano eodem, aequalia rectangulo NXF, multiplici per numerum particularum ipsarum sectionis NN, vel segmenti NMMN. Est autem BD divisa similiter in C & K, atque NN in X & F. Ergo rectangulum BCK ad rectangulum NXF, sicut quadratum BD ad quadratum NN. Est autem & numerus particularum sectionis BD, ad numerum particularum sectionis NN, sicut sectiones ipsae; hoc est, sicut quadratum BD ad quadratum NN. Itaque rectangulum BCK, multiplex per numerum particularum sectionis BD, ad rectangulum NXF, multiplex per numerum particularum sectionis NN, dupli|catam habebitGa naar margenoot+ rationem quadrati BD ad quadratum NN; hoc est, eam quam quadratum VV ad quadratum RR, in figura proportionali. Erit igitur & dicta prior summa quadratorum, à distantiis particularum segmenti BNND à plano EC, ad summam alteram quadratorum, à distantiis particularum segmenti NMMN, ut qu. VV ad qu. RR. Eademque ratione ostendetur, summas quadratorum à distantiis particularum in reliquis segmentis solidi ABCD, esse inter se in ratione quadratorum quae fiunt à rectis in figura OVV, quae basi cujusque segmenti respondent. Quare summa quadratorum, à distantiis particularum omnium segmentorum solidi ABCD à plano EC, erit ad summam quadratorum, à distantiis particularum segmentorum totidem, maximo segmento aequalium, hoc est, cylindri vel prismatis BDSS, eandem cum solido ABCD basin altitudinemque habentis, sicut quadrata omnia rectarum VV, RR, QQ, &c. ad quadrata totidem maximo VV aequalia, hoc est, sicut solidum rotundum OVV circa axem OP, ad cylindrum VVΩΩ, qui basin & altitudinem habeat eandem. Hanc vero rationem solidi OVV ad cylindrum VVΩΩ, componi constat ex ratione planorum quorum | |||||||||||||||||||||||||||||||||||
[pagina 292]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ de la raison des plans par la rotation desquels ils sont engendrés, c.à.d. celle du plan OPV au rectangle PΩ, et de la raison des distances à l'axe OP des centres de gravité de ces plans, c.à.d. de celle de PΦ à P ∆. Et la première de ces raisons, savoir celle du plan OPV au rectangle PΩ, est la même que celle du solide ABCD au cylindre ou prisme BDSS, c.à.d. la même que celle du nombre des particules du solide ABCD à celui des particules du cylindre ou prisme BDSS. Et l'autre raison, celle de PΦ à P ∆ est la même, par construction, que celle de l'espace Z au rectangle BCK. La dite somme des carrés des distances de toutes les particules du solide ABCD au plan EC a donc à la somme des carrés des distances de toutes les particules du cylindre ou prisme BDSS à ce même plan un rapport composé de la raison du nombre des particules du solide ABCD à celui des particules du cylindre ou prisme BDSS et de la raison de l'espace Z au rectangle BCK, en d'autres termes un rapport égal à celui du rectangle Z multiplié par le nombre des particules du solide ABCD au rectangle BCK multiplié par le nombre des particules du cylindre ou prisme BDSS. Mais la quatrième de ces grandeurs est égale à la deuxième, c.à.d. le rectangle BCK multiplié par le nombre des particules du cylindre ou prisme BDSS est égal à la somme des carrés des distances des particules de ce même prisme ou cylindre BDSS au plan EC, puisque ce rectangle BCK, multiplié par le nombre des particules du segment BNND, est égal à la somme des carrés des distances des particules de ce segment au plan ECGa naar margenoot*. Par conséquent le troisième terme de la proportion sera aussi égal au premier; c.à.d. le plan Z, multiplié par le nombre des particules du solide ABCD, sera égal à la somme des carrés des distances des particules du même solide ABCD au plan ECGa naar margenoot*. C. Q. F. D. | |||||||||||||||||||||||||||||||||||
[pagina 293]
| |||||||||||||||||||||||||||||||||||
 [Fig. 90.]Ga naar margenoot+
conversione generantur, hoc est, ex ratione plani OPV, ad rectangulum PΩ, & ex ratione distantiarum quibus horum planorum centra gravitatis absunt ab axe OP; hoc est, & ex ratione PΦ ad P∆. Et prior quidem harum rationum, nempe plani OPV ad rectangulum PΩ, eadem est quae solidi ABCD ad cylindrum vel prisma BDSS, hoc est, eadem quae numeri particularum solidi ABCD, ad numerum particularum cylindri vel prismatis BDSS. Altera vero ratio, nempe PΦ ad P∆, est eadem, ex constructione, quae spatii Z ad rectangulum BCK. Habebit itaque dicta summa quadratorum, à distantiis omnium particularum solidi ABCD à plano EC, ad summam quadratorum, à distantiis omnium particularum cylindri vel prismatis BDSS ab eodem plano, rationem eam quae componitur ex ratione numeri particularum solidi ABCD, ad numerum particularum cylindri vel prismatis BDSS, & ex ratione spatii Z ad rectangulum BCK: hoc est, rationem quam habet rectangulum Z, multiplex per numerum particularum solidi ABCD, ad rectangulum BCK, multiplex per numerum particularum cylindri vel prismatis BDSS. Atqui quarta harum magnitudinum aequalis est secundae; nempe rectangulum BCK, multiplex per numerum particularum cylindri vel prismatis BDSS, aequale summae quadratorum, à distantiis particularum ejusdem prismatis vel cylindri BDSS à plano EC; siquidem rectangulum idem BCK, multiplex | per numerum particularumGa naar margenoot+ segmenti BNND, aequatur quadratis distantiarum particularum ejusdem segmenti à plano ECGa naar margenoot*. Ergo & tertia primae aequabitur, nempe planum Z, multiplex per numerum particularum solidi ABCD, summae quadratorum, à distantiis particularum solidi ejusdem ABCD à plano ECGa naar margenoot*. quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||
[pagina 294]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Il faut encore remarquer que lorsque le solide ABD est de révolution autour de l'axe AC, le rectangle BCK devient toujours égal au quart de BC2, puisque la subcentrique BK de l'onglet coupé sur le cercle BD par un plan passant par la tangente en B est égale à 5/4 fois le rayon BCGa naar voetnoot1). Par conséquent, si PV est prise égale à BC, il s'ensuit, si l'on veut que P ∆ soit à P Φ comme le rectangle BCK, c.à.d. le quart du carré de BC ou bien P ∆2, est à un autre plan Z, que ce dernier sera égal au rectangle ∆P Φ. Il s'ensuit donc aussi que ce rectangle ∆P Φ, multiplié par le nombre des particules du solide ABD, sera égal à la somme cherchée des carrés de toutes les perpendiculaires abaissées de ces particules sur le plan EC. | |||||||||||||||||||||||||||||||||||
Proposition XVI.Lorsqu'une figure quelconque, ligne, surface ou solide, est diversement suspendue et oscille autour d'axes parallèles les uns aux autres et également distants du centre de gravité de la figure, celle-ci est isochrone avec elle-mêmeGa naar voetnoot2).
Considérons une grandeur quelconque [Fig. 91] dont E soit le centre de gravité; qu'elle soit d'abord suspendue à un axe passant par le point F et perpendiculaire au plan de cette page. Ce dernier sera donc le plan d'oscillation. Si l'on décrit dans ce plan du centre E, avec le rayon EF, la circonférence FHG et qu'ayant pris sur elle un point quelconque tel que H, on suppose en second lieu que la grandeur soit suspendue à un axe passant par ce point et oscille autour de lui, le plan d'oscillation demeurant le même, je dis qu'elle sera isochrone avec elle-même oscillant autour de l'axe F. En effet, supposons la grandeur considérée divisée en particules égales et fort petites. Il est donc manifeste que, comme le plan d'oscillation demeure le même dans les deux suspensions à l'égard des parties de la grandeur, les perpendiculaires qu'on peut abaisser de toutes les particules de la grandeur sur le dit plan d'oscillation auront leurs pieds aux mêmes endroits dans l'une et l'autre suspension. Soient ces endroits les points marqués dans l'espace ABCD. Comme donc E est le centre de gravité de la grandeur proposée et que celle-ci garde par conséquent dans n'importe quelle position l'équilibre autour de l'axe qui est érigé à travers le point E perpendiculairement au plan ABCD, on voit aisément que si une gravité égale est attribuée à tous les points marqués dans l'espace ABCD dont nous venons de parler, le point E sera aussi le centre de gravité de tous ces points-là. Mais si, comme il peut arriver, plusieurs perpendiculaires coïncident en certains points, ceux-ci doivent être considérés comme doublés autant de fois et leurs gravités comme autant de fois multiples. Lorsqu'on les envisage de cette façon, il paraît que le point E est de nouveau leur centre de gravité. | |||||||||||||||||||||||||||||||||||
[pagina 295]
| |||||||||||||||||||||||||||||||||||
Notandum vero, quando solidum ABD rotundum est circa axem AC, fieri semperGa naar margenoot+ rectangulum BCK aequale quartae parti quadrati BC; quoniam subcentrica cunei, abscissi super circulo BD, plano per tangentem in B, nempe recta BK, aequatur 5/4 radii BC. Unde, si PV aequalis posita sit BC, sequitur, faciendo ut P∆ ad PΦ ita rectangulum BCK, hoc est, ¼ quadrati BC, hoc est, qu P∆ ad planum aliud Z, fore hoc rectangulo ∆PΦ aequale. Ac proinde tunc ipsum rectangulum ∆PΦ, multiplex secundum numerum particularum solidi ABD, aequari summae quaesitae quadratorum à perpendicularibus omnibus, quae à particulis iisdem cadunt in planum EC. | |||||||||||||||||||||||||||||||||||
Propositio XVI.Figura quaevis, sive linea fuerit, sive superficies, sive solidum; si aliter atque aliter suspendatur, agiteturque super axibus inter se parallelis, quique à centro gravitatis figurae aequaliter distent, sibi ipsi isochrona estGa naar voetnoot2). 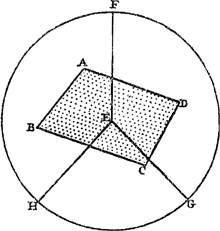 [Fig. 91.]
Proponatur magnitudo quaevis [Fig. 91], cujus centrum gravitatis E punctum, sitque primo suspensa ab axe, qui per F intelligitur hujus paginae plano ad angulos rectos. Itaque idem planum erit & planum oscillationis. In quo si centro E, radio EF, describatur circumferentia FHG, sumptoque in illa puncto quovis, ut H, magnitudo secundò suspendi intelligatur ab axe in hoc puncto infixo, atque agitari, manente eodem oscillationis plano. Dico isochronam fore sibi ipsi agitatae circa axem in F. Intelligatur enim dividi magnitudo propositaGa naar margenoot+ in particulas minimas aequales. Itaque, quia in utraque illa suspensione idem manet oscillationis planum, respectu partium magnitudinis; manifestum est, si ab omnibus particulis, in quas divisa est magnitudo, perpendiculares cadere concipiantur in dictum oscillationis planum, illas utraque suspensione occurrere ipsi in punctis iisdem. Sint autem haec puncta ea quae apparent in spatio ABCD. Quum igitur E sit centrum gravitatis magnitudinis propositae, ipsaque proinde circa axem, qui per E punctum erectus est ad planum ABCD, quovis situ aequilibrium servet; facile perspicitur, quod si punctis omnibus ante dictis, quae in spatio ABCD signantur, aequalis gravitas tribuatur, eorum quoque omnium centrum gravitatis futurum est punctum E. Quod si vero, ut fieri potest, in puncta aliqua plures perpendiculares coincidant, illa puncta quasi toties geminata intelligenda sunt, gravitatesque toties multiplices accipiendae. Atque ita consideratorum, patet rursus centrum gravitatis esse E punctum. | |||||||||||||||||||||||||||||||||||
[pagina 296]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Il est maintenant évident que la somme des carrés des droites qui relient tous les dits points au point F est égale à la somme des carrés des perpendiculaires abaissées de toutes les particules de la grandeur proposée sur l'axe d'oscillation passant par F, attendu que les lignes dont nous considérons ici les carrés ont dans l'un et l'autre cas les mêmes longueurs. Pareillement, lorsque la grandeur considérée est suspendue à un axe passant par H, il apparaît que la somme des carrés des droites qui relient au point H tous les points marqués dans l'espace ABCD est égale à celle des carrés des perpendiculaires abaissées de toutes les particules de la grandeur proposée sur l'axe d'oscillation passant par H. Par conséquent si, dans l'un et l'autre cas, la somme des carrés des droites qui relient tous les points susdits aux points F ou H est divisée par les droites EF ou EH, multipliées chacune par le nombre des particules dans lesquelles la grandeur proposéé est divisée par hypothèse, de cette division résultera la longueur d'un pendule simple isochrone avec la grandeur suspendue en F ou H. Or, la somme des carrés est égale dans les deux casGa naar margenoot* et les droites EF, EH sont aussi égales entre elles, et le nombre des particules est le même. Par conséquent, comme les dénominateurs et les numérateurs des deux expressions considérées sont égaux, les longueurs résultant de la division le seront aussi, c.à.d. il y aura égalité des deux pendules isochrones avec la grandeur proposée suspendue d'abord en F puis en H. La proposition est donc établie. | |||||||||||||||||||||||||||||||||||
Proposition XVII.Étant donné un plan qui, multiplié par le nombre des particules dans lesquelles la figure suspendue est divisée par la pensée, donne un produit égal à la somme des carrés des distances de l'axe d'oscillation, la longueur du pendule simple isochrone avec la figure résultera de la division de ce plan par une droite égale à la distance de l'axe d'oscillation au centre de gravité de la grandeur suspendue.
Soit ABC [Fig. 92] la figure à centre de gravité E suspendue à un axe passant par le point F perpendiculairement au plan qui est vu ici. Et supposant la figure divisée en particules égales fort petites, de chacune desquelles on doit se figurer qu'une perpendiculaire a été abaissée sur le dit axe, soit trouvé, d'après les règles sus-énoncées, le plan H qui, multiplié par le nombre des dites particules, donne un produit égal à la somme des carrés de toutes ces perpendiculaires. Que la division du plan H par la droite FE donne la longueur FG. Je dis que celle-ci représente la longueur du pendule simple exécutant des oscillations isochrones avec celles de la grandeur ABC autour de l'axe F. | |||||||||||||||||||||||||||||||||||
[pagina 297]
| |||||||||||||||||||||||||||||||||||
Porrò summam quadratorum ab rectis, quae ducuntur à dictis punctis omnibus adGa naar margenoot+ punctum F, eandem esse patet cum summa quadratorum ab iis rectis, quae à singulis particulis magnitudinis propositae ducuntur perpendiculares in axem oscillationis per F transeuntem; quippe cum lineae ipsae, quarum quadratra intelliguntur, utrobique eandem habeant longitudinem. Similiter etiam, cum suspensio est ex axe per H, patet summam quadratorum ab rectis, quae ab omnibus punctis, in spatio ABCD signatis, ducuntur ad punctum H, eandem esse cum summa quadratorum, ab iis quae, à particulis omnibus magnitudinis propositae, ducuntur perpendiculares in axem oscillationis per H transeuntem. Ergo utroque casu, si summa quadratorum ab rectis quae, à punctis omnibus praedictis, ducuntur ad puncta F vel H, dividatur per rectas EF vel EH, multiplices secundum numerum particularum in quas magnitudo proposita divisa intelligitur, orietur ex applicatione hac longitudo penduli simplicis, quod magnitudini suspensae ex F vel H isochronum sit. Est autem summa quadratorum utroque casu aequalisGa naar margenoot*; & rectae quoque EF, EH, inter se aequales; & particularum idem numerus. Ergo, quum & applicatae quantitates, & quibus illae applicantur, utrobique aequales sint, etiam longitudines ex applicatione ortae aequales erunt, hoc est, longitudines pendulorum isochronorum magnitudini propositae suspensae ex F vel ex H. Quare constat propositum. | |||||||||||||||||||||||||||||||||||
Propositio XVII.Ga naar margenoot+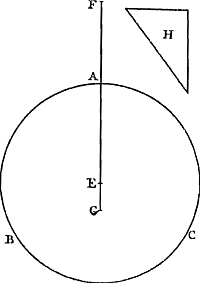 [Fig. 92.]
Dato plano, cujus multiplex per numerum particularum, in quas suspensa figura divisa intelligitur, aquetur quadratis omnium distantiarum ab axe oscillationis; si illud applicetur ad rectam aequalem distantiae inter axem oscillationis & centrum gravitatis suspensae magnitudinis, orietur longitudo penduli simplicis ipsi isochroni.
Sit figura ABC [Fig. 92], cujus centrum gravitatis E, suspensa ab axe qui, per F punctum ad planum quod conspicitur, erectus sit. Ponendoque divisam figuram in particulas minimas aequales, à quibus omnibus, in dictum axem, perpendiculares cadere intelligantur: esto, per superius ostensa, inventum planum H, cujus multiplex per numerum dictarum particularum, aequetur quadratis omnibus dictarum perpendicularium. Applicatoque plano H ad rectam FE, fiat longitudo FG. Dico hanc esse longitudinem penduli simplicis, isochronas oscillationes habentis magnitudini ABC, agitatae circa axem per F. | |||||||||||||||||||||||||||||||||||
[pagina 298]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ En effet, comme la somme des carrés des distances de l'axe F, divisée par la distance FE multipliée par le nombre des particules, constitue la longueur du pendule simple isochroneGa naar margenoot*, et qu'à cette somme de carrés multipliée par le même nombre, celui des particules, est égale par hypothèse le plan H; il s'ensuit que si l'on divise le plan H multiplié par le nombre des particules, par la distance FE multipliée par le nombre des particules, ou bien, en omettant le facteur commun, si l'on divise le plan H par la distance FE, il en résultera aussi la longueur du pendule simple isochrone. Il apparaît donc que cette longueur est FG, comme nous l'avions dit. C. Q. F. D. | |||||||||||||||||||||||||||||||||||
Proposition XVIII.Si l'espace plan qui, multiplié par le nombre des particules de la grandeur suspendue, est égal à la somme des carrés des distances à l'axe de gravité (parallèle à l'axe d'oscillation), est divisé par une droite égale à la distance des deux axes nommés, il en résultera une droite égale à l'intervalle, duquel le centre d'oscillation est inférieur au centre de gravité de la même grandeurGa naar voetnoot1).
Soit ABCD [Fig. 93] une grandeur à centre de gravité E, qui ait le centre d'oscillation G lorsqu'elle est suspendue à un axe passant par le point F perpendiculairement au plan de cette page. Figurons-nous de plus un autre axe parallèle à celui passant par F et traversant le centre de gravité E. Et la grandeur ayant été divisée par la pensée en de très petites particules égales, soit le plan I multiplié par le nombre de ces particules égal à la somme des carrés des distances au dit axe passant par E. La division du plan I par la distance FE nous donne une certaine droite. Je dis qu'elle est égale à l'intervalle EG duquel le centre d'oscillation est inférieur au centre de gravité de la grandeur ABCD. En effet, qu'on se figure pour que notre démonstration de cette proposition soit | |||||||||||||||||||||||||||||||||||
[pagina 299]
| |||||||||||||||||||||||||||||||||||
Quia enim summa quadratorum, à distantiis ab axe F, applicata ad distantiam FE,Ga naar margenoot+ multiplicem secundum partium numerum, facit longitudinem penduli simplicis isochroniGa naar margenoot*. Isti vero quadratorum summae aequale ponitur planum H, multiplex per eundem particularum numerum. Ergo & planum H, multiplex per eundem particularum numerum, si applicetur ad distantiam FE, multiplicem | secundum particularumGa naar margenoot+ numerum; sive, omissa communi multiplicitate, si planum H applicetur ad distantiam FE; orietur quoque longitudo penduli simplicis isochroni. Quam proinde ipsam longitudinem FG esse constat. quod erat demonstrandum. | |||||||||||||||||||||||||||||||||||
Propositio XVIII.Si spatium planum, cujus multiplex secundum numerum particularum suspensae magnitudinis, aequetur quadratis distantiarum ab axe gravitatis, axi oscillationis parallelo; id, inquam, spatium si applicetur ad rectam, aequalem distantiae inter utrumque ditorum axium, orietur recta aequalis intervallo, quo centrum oscillationis inferius est centro gravitatis ejusdem magnitudinisGa naar voetnoot1). 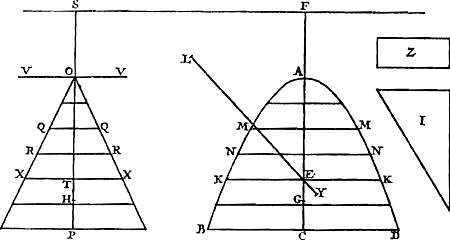 [Fig. 93.]
Esto magnitudo ABCD [Fig. 93], cujus centrum gravitatis E; quaeque suspensa ab |axe, qui per punctum F ad planum hujus paginae erectus intelligitur, habeat centrum oscillationis G. Porrò axi per F intelligatur axis alius, per centrum gravitatis E transiens, parallelus. Divisaque magnitudine cogitatu in particulas minimas aequales, sit quadratis distantiarum, ab axe dicto per E, aequale planum I, multiplex nempe secundum numerum dictarum particularum; applicatoque plano I ad distantiam FE, fiat recta quaedam. Dico eam aequalem esse intervallo EG, quo centrum oscillationis inferius est centro gravitatis magnitudinis ABCD. Ut enim universali demonstratione quod propositum est comprehendamus: intelli- | |||||||||||||||||||||||||||||||||||
[pagina 300]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ universelle, une figure plane OQP analogue à la grandeur ABCD et placée à côté d'elle; il s'agit d'une figure qui, coupée par les mêmes plans horizontaux que la grandeur ABCD, ait ses segments, compris entre deux quelconques de ces plans, proportionnels aux segments correspondants de la dite grandeur. Supposons en outre chaque segment de la figure OQP divisé en un nombre de particules égales qui soit le même que celui du segment correspondant de la figure ABCD. Or, on peut se figurer cette construction exécutée quelle que soit la grandeur ABCD, en d'autres termes que ce soit une ligne, une surface ou un corps solide. Il est évident que toujours le centre de gravité T de la figure OQP est situé à la même hauteur que celui de la grandeur ABCD, et que par conséquent, si le plan horizontal passant par F coupe la ligne du centreGa naar voetnoot1) de la figure OQP par exemple en S, les distances ST et FE sont égales. Au reste il est constant que les carrés des distances de l'axe d'oscillation F, divisés par la distance FE multipliée par le nombre des particules, donnent la longueur du pendule isochroneGa naar margenoot*, que nous avons appelée FG. Or, on voit aisément que la somme de ces carrés est égale aux carrés des distances au plan horizontal passant par F plus les carrés des distances au plan vertical FE passant par l'axe F et le centre de gravité EGa naar margenoot*. Mais les carrés des distances de la grandeur ABCD au plan horizontal passant par F sont égaux aux carrés des distances de la figure OQP à la droite SF. Lesquels carrés (si O est le point le plus haut de la figure OQP et OH la subcentrique de l'onglet coupé sur lui par un plan passant par la droite OV parallèle à SF) sont égaux à la somme du rectangle OTH et du carré ST, multipliés chacun par le nombre des particules de la dite figureGa naar margenoot*, c.à.d. de la grandeur ABCD. Or, les carrés des distances de la grandeur ABCD au plan FE sont toujours les mêmes, quelle que soit la distance de l'axe d'oscillation F au centre de gravité E; posons qu'ils soient égaux au produit d'un espace Z par le nombre des particules de la grandeur ABCD. Par conséquent, comme les carrés des distances de la grandeur ABCD à l'axe d'oscillation F sont égaux au carré de ST plus le rectangle OTH plus le plan Z, multipliés chacun par le nombre des particules égales, si cette expression entière est divisée par la distance FE ou ST, il en résultera la longueur FG du pendule isochrone avec la grandeur ABCDGa naar margenoot*. Mais de la division de ST2 per son côté ST, résulte ST ou FE elle-même. Le reste EG est donc le quotient du rectangle OTH augmenté du plan Z par la même longueur ST ou FE. C'est pourquoi il reste à prouver que le rectangle OTH augmenté du plan Z est égal au plan I. En effet, ceci étant démontré, il sera établi que la division du plan I par la distance FE donne aussi une longueur égale à EG. Or, nous le prouverons comme suit. Le rectangle OTH, multiplié par le nombre des particules de la figure OQP ou de la grandeur ABCD, est égal aux carrés des distances de la figure de la droite XTGa naar margenoot* tirée par le centre de gravité T parallèlement à SF; il est donc aussi égal aux | |||||||||||||||||||||||||||||||||||
[pagina 301]
| |||||||||||||||||||||||||||||||||||
gatur plana figura, magnitudini ABCD analoga, ad latus adposita, OQP; quae nempe,Ga naar margenoot+ secta planis horizontalibus iisdem cum magnitudine ABCD, habeat segmenta inter|cepta inter bina quaeque plana, in eadem inter se ratione cum segmentis dictaeGa naar margenoot+ magnitudinis, quae ipsis respondent; sintque segmenta singula figurae OQP, divisa in tot particules aequales, quot continentur segmentis ipsis respondentibus in figura ABCD. Haec autem intelligi possunt fieri, qualiscunque fuerit magnitudo ABCD, sive linea, sive superficies, sive solidum. Semper vero centrum gravitatis figurae OQP, quod sit T, eadem altitudine esse manifestum est cum centro gravitatis magnitudinis ABCD; ideoque, si planum horizontale, per F ductum, secet lineam centriGa naar voetnoot1) figurae OQP, velut hic in S, aequales esse distantias ST, FE. Porrö autem constat quadrata distantiarum, ab axe oscillationis F, applicata ad distantiam FE, multiplicem secundum numerum particularum, efficere longitudinem penduli isochroniGa naar margenoot*; quae longitudo posita fuit FG. Illorum vero quadratorum summam, aequalem esse perspicuum est, quadratis distantiarum à plano horizontali per F, unà cum quadratis distantiarum à plano verticali FE, per axem F & centrum gravitatis E ductoGa naar margenoot*. Atqui quadrata distantiarum magnitudinis ABCD à plano horizontali per F, aequantur quadratis distantiarum figurae OQP ab recta SF. Quae quadrata (si O sit punctum supremum figurae OQP, & OH subcentrica cunei super ipsa abscissi, plano per rectam OV, parallelam SF) aequalia sunt rectangulo OTH & quadrato ST, multiplicibus secundum numerum particularum dictae figuraeGa naar margenoot*, sive magnitudinis ABCD. Quadrata vero distantiarum magnitudinis ABCD à plano FE, quantumcunque axis oscillationis F distet à centro gravitatis E, semper eadem sunt: quae proinde putemus aequari spatio Z, multiplici secundum numerum particularum magnitudinis ABCD. Itaque quoniam quadrata distantiarum magnitudinis ABCD, ab axe oscillationis F, aequantur istis, quadrato nimirum ST, rectangulo OTH, & plano Z, multiplicibus per numerum particularum ejusdem magnitudinis; si applicentur haec omnia ad distantiam FE sive ST, orietur longitudo FG penduli isochroni magnitudini ABCDGa naar margenoot*. Sed ex applicatione quadrati ST ad latus suum ST, orietur ipsa ST, sive FE. Ergo reliqua EG est ea quae oritur ex applicatione rectanguli OTH, & plani Z, ad eandem ST vel FE. Quare superest ut demonstremus rectangulum OTH, cum plano Z, aequari plano I. Tunc enim constabit, etiam planum I, applicatum ad distantiam FE, efficere longitudinem ipsi EG aequalem. Illud autem sic ostendetur. Rectangulum OTH, multiplex secundum numerum particularum figurae OQP, sive magnitudinis AB|CD, aequaturGa naar margenoot+ quadratis distantiarum figurae ab recta XTGa naar margenoot*, quae per centrum gravitatis T ducitur | |||||||||||||||||||||||||||||||||||
[pagina 302]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ carrés des distances de la grandeur ABCD au plan horizontal KK mené par le centre de gravité E, puisque les distances sont les mêmes dans l'un et l'autre cas. Mais le plan Z, multiplié par le même facteur, fut posé égal aux carrés des distances de la grandeur ABCD au plan vertical FE. Et il est évident que ces carrés des distances au plan FE, augmentés des dits carrés des distances au plan horizontal passant par E, sont égaux aux carrés des distances à l'axe de gravité passant par E parallèlement à l'axe FGa naar margenoot*. Par conséquent le rectangle OTH augmenté du plan Z, multipliés l'un et l'autre par le nombre des particules de la grandeur ABCD, seront égaux aux carrés des distances de la même grandeur au dit axe passant par E. Mais le plan I lui aussi, multiplié par le même nombre des particules, fut posé égal à ces mêmes carrés des distances. Par conséquent le plan I est égal à la somme du rectangle OTH et du plan Z. C'est ce qu'il restait à démontrer. Cette proposition fait voir de nouveau ce qui a été démontré dans la Prop. XVI, savoir qu'une grandeur quelconque est isochrone avec elle-même lorsqu'elle est diversement suspendue et oscille chaque fois autour d'un axe parallèle aux autres, tous les axes étant également distants du centre de gravité. En effet, qu'une grandeur ABCD soit suspendue à l'axe F ou bien à l'axe L qui lui est parallèle, il est évident que dans les deux cas les carrés des distances d'un axe parallèle aux axes F et L et passant par E sont les mêmes. Par conséquent le plan I dont le produit par le nombre des particules est égal à la somme des carrés, sera le même dans l'un et l'autre cas. Mais ce plan, divisé par la distance du centre de gravité à l'axe d'oscillation, laquelle est par hypothèse la même dans les deux cas, donne la distance de laquelle le centre d'oscillation est inférieur au centre de gravité; cette distance sera donc la même dans les deux cas. Par exemple, si dans le cas de la suspension en L la dite distance est EY, celle-ci sera égale à EG et la droite entière YL à GF. Pour les deux suspensions le même pendule simple sera donc isochrone avec la grandeur ABCD. | |||||||||||||||||||||||||||||||||||
Proposition XIX.Lorsqu'une même grandeur oscille, la suspension étant tantôt plus courte et tantôt plus longue, les distances des centres d'oscillation au centre de gravité, qui reste le même, seront inversement proportionnelles aux distances des axes d'oscillation à ce centre de gravitéGa naar voetnoot1).
Supposons qu'une grandeur à centre de gravité A [Fig. 94] soit d'abord suspendue et agitée autour d'un axe B, ensuite autour d'un axe C, et que le centre d'oscillation soit D dans le premier cas, E dans le second. Je dis qu'on a BA : CA = EA : DA. En effet, comme dans le cas de la suspension en B la distance AD, de laquelle le centre d'oscillation est inférieur au centre de gravité, est obtenue en divisant par la distance BA un espace dont le produit par le nombre des très petites particules éga- | |||||||||||||||||||||||||||||||||||
[pagina 303]
| |||||||||||||||||||||||||||||||||||
ipsi SF parallela; ac proinde etiam quadratis distantiarum magnitudinis ABCD, àGa naar margenoot+ plano horizontali KK, ducto per centrum gravitatis E; cum distantiae utrobique sint eaedem. At vero planum Z, similiter multiplex, aequale positum fuit quadratis distantiarum magnitudinis ABCD à plano verticali FE. Ac patet quidem quadrata haec distantiarum à plano FE, una cum dictis quadratis distantiarum à plano horizontali per E, aequalia esse quadratis distantiarum ab axe gravitatis per E, qui sit axi F parallelusGa naar margenoot*. Itaque rectangulum OTH una cum plano Z, multiplicia secundum numerum particularum magnitudinis ABCD, aequalia erunt quadratis distantiarum ejusdem magnitudinis à dicto axe per E. Sed & planum I, multiplex secundum eundem particularum numerum, aequale positum fuit iisdem distantiarum quadratis. Ergo planum I aequale est rectangulo OTH & plano Z simul sumptis. quod ostendendum supererat. Hinc rursus manifestum fit, quod propositione 16 demonstratum fuit; nempe magnitudinem quamlibet, si aliter atque aliter suspendatur atque agitetur, ab axibus parallelis, qui à centro gravitatis suae aequaliter distent, sibi ipsi isochronam esse. Sive enim magnitudo ABCD suspendatur ab axe F, sive ab axe L illi parallelo; patet eadem utrobique esse quadrata distantiarum ab axe per E, qui sit axibus F vel L parallelus. Unde & planum I, cujus multiplex, secundum numerum particularum, aequatur quadratorum summae, utroque casu idem erit. Hoc vero planum, applicatum ad distantiam centri gravitatis ab axe oscillationis, quae utroque casu eadem ponitur, efficit distantiam qua centrum oscillationis inferius est centro gravitatis; Ergo etiam haec distantia utroque casu eadem erit. Velut si, facta suspensione ex L, fuerit dicta distantia EY, erit ipsa aequalis EG; & tota YL aequalis GF; adeoque, in suspensione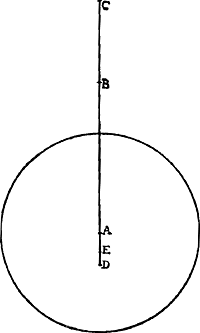 utraque, idem pendulum simplex isochronum sit magnitudini ABCD.
utraque, idem pendulum simplex isochronum sit magnitudini ABCD.
| |||||||||||||||||||||||||||||||||||
Propositio XIX.Si magnitudo eadem, nunc brevius nunc longius suspensa, agitetur; erunt, sicut distantiae axium oscillationis à centro gravitatis inter se, ita contraria ratione distantiae centrorum oscillationis ab eodem gravitatis centroGa naar voetnoot1).
Sit magnitudo, cujus centrum gravitatis A, suspensa primum atque agitata ab axe in B, deinde vero ab axe in C; sitque in prima | suspensione centrumGa naar margenoot+ oscillationis D, in posteriori vero centrum oscillationis E. Dico esse ut BA ad CA ita EA ad DA. Quum enim, in suspensione ex B, efficiatur distantia AD, qua nempe centrum oscillationis inferius est centro gravitatis, applicando ad distantiam BA spatium quoddam, cujus multiplex secundum numerum | |||||||||||||||||||||||||||||||||||
[pagina 304]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ les dans lesquelles la grandeur est divisée par la pensée est égal aux carrés des distances à un axe passant par A parallèlement a l'axe BGa naar margenoot*, le rectangle BAD sera égal au dit espace. De même dans le cas de la suspension en C, comme la distance AE est obtenue par la division du dit espace par la distance CA, le rectangle CAE lui aussi sera égal à ce même espace. Les rectangles BAD et CAE sont donc égaux entre eux; partant le rapport BA : CA est le même que AE : AD. C. Q. F. D. Il en résulte évidemment que lorsqu'un pendule simple isochrone avec la grandeur suspendue est donné pour une suspension déterminée, et que le centre de gravité de la grandeur est connu, la longueur du pendule isochrone est également connue pour toute autre suspension plus courte ou plus longue, pourvu que le plan de l'oscillation reste le même. | |||||||||||||||||||||||||||||||||||
Proposition XX.Le centre d'oscillation et le point de suspension sont réciproquesGa naar voetnoot1).
Dans la figure qui précède [Fig. 94] le centre d'oscillation est D lorsque le corps est suspendu en B; mais lorsqu'on invertit toutes choses et qu'on suppose le corps suspendu en D, le centre d'oscillation sera B. C'est ce qui résulte clairement de la proposition précédente. | |||||||||||||||||||||||||||||||||||
Proposition XXI.Comment on trouve les centres d'oscillation dans les figures planesGa naar voetnoot2).
Lorsqu'on a compris ce qui a été démontré jusqu'ici, il sera désormais facile de définir les centres d'oscillation dans la plupart des figures qu'on a coutume de considérer en géométrie. Et pour parler d'abord des figures planes, nous avons défini plus haut pour elles deux oscillations différentes, savoir celle autour d'un axe situé dans le plan de la figure et celle autour d'un axe perpendiculaire à ce plan, dont nous avons appelé la première plane et la deuxième latérale. Que si la figure est mise en mouvement de la première façon, savoir autour d'un | |||||||||||||||||||||||||||||||||||
[pagina 305]
| |||||||||||||||||||||||||||||||||||
 [Fig. 94.]
particularum minimarum aequalium, in quas magnitudoGa naar margenoot+ divisa intelligitur, aequatur quadratis distantiarum ab axe per A, parallelo axi in BGa naar margenoot*; erit proinde rectangulum BAD dicto spatio aequale. Item in suspensione ex C, quum fiat distantia AE, applicando idem dictum spatium ad distantiam CA; erit & rectangulum CAE eidem spatio aequale. Itaque aequalia inter se rectangula BAD, CAE; ac proinde ratio BA ad CA eadem quae AE ad AD. quod erat demonstrandum. Hinc patet, dato pendulo simplici, quod magnitudini suspensae isochronum sit in una suspensione, datoque ejus centro gravitatis; etiam in alia omni suspensione, longiori vel breviori, dummodo idem maneat planum oscillationis, longitudinem penduli isochroni datam esse. | |||||||||||||||||||||||||||||||||||
Propositio XX.Centrum Oscillationis & punctum suspensionis inter se convertunturGa naar voetnoot1).
In figura superiori [Fig. 94], quia, posita suspensione ex B, centrum oscillationis est D; etiam invertendo omnia, ponendoque suspen|sionem ex D, erit tunc centrumGa naar margenoot+ oscillationis B. Hoc enim ex ipsa propositione praecedenti manifestum est. | |||||||||||||||||||||||||||||||||||
Propositio XXI.Quomodo in figuris planis centra oscillationis invenianturGa naar voetnoot2).
Intellectis quae hactenus demonstrata sunt, facile jam erit in plerisque figuris, quae in Geometria considerari consueverunt, definire oscillationis centra. Atque ut de planis figuris primum dicamus; duplicem in iis oscillationis motum supra definivimus; nempe, vel circa axem in eodem cum figura plano jacentem, vel circa eum qui ad figurae planum erectus sit. Quorum priorem vocavimus agitationem in planum, alterum agitationem in latus. Quod si priore modo agitetur, nempe circa axem in eodem plano jacentem, sicut | |||||||||||||||||||||||||||||||||||
[pagina 306]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ axe situé dans son plan, par exemple la figure BCD autour de l'axe EF [Fig. 95], on obtiendra le centre d'oscillation K de cette figure de la manière suivante. Considérons l'onglet coupé sur la figure par un plan qui traverse celui de la figure de telle manière que l'intersection DD est parallèle à l'axe d'oscillation. Soit donnée la distance AD du centre de gravité de la figure à cette intersection, ainsi que la subcentrique DH du dit onglet par rapport à la même intersection. C'est en divisant le rectangle DAH par la distance FA qu'on trouve le centre d'oscillation K de la figure BDC, puisque cette division donne la distance AK de laquelle le centre d'oscillation est inférieur au centre de gravité. En effet, le rectangle DAH, multiplié par le nombre des particules de la figure BCD, est égal aux carrés des distances à la droite BAC parallèle à l'axe d'oscillation EF et passant par le centre de gravité AGa naar margenoot*. Par conséquent la division du même rectangle par la distance FA nous donnera la distance AK de laquelle le centre d'oscillation est inférieur au centre de gravité AGa naar margenoot*. Il est donc manifeste que si DD est l'axe d'oscillation, le centre d'oscillation tombe en H et que conséquemment la longueur DH du pendule simple isochrone avec la figure BCD est alors précisément la subcentrique par rapport à DD de l'onglet limité par un plan passant par la même droite DD. Ceci seul avait été remarqué avant moi par d'autres, sans toutefois qu'ils l'eussent démontréGa naar voetnoot1). Il n'entre pas dans notre plan d'exposer comment on trouve les centres de gravité des onglets coupés sur des figures planes, et déjà ils sont connus dans beaucoup de cas. Par exemple si la figure BCD est un cercle, DH sera égale à ⅝ fois le diamètre. Si c'est un rectangle, on aura DH = ⅔ du diamètre. D'où paraît la raison pour laquelle une verge, ou ligne pesante, suspendue par un de ses bouts est isochrone avec un pendule d'une longueur de ⅔ de la sienne; savoir en considérant cette ligne comme si c'était un rectangle de largeur extrêmement petite. | |||||||||||||||||||||||||||||||||||
[pagina 307]
| |||||||||||||||||||||||||||||||||||
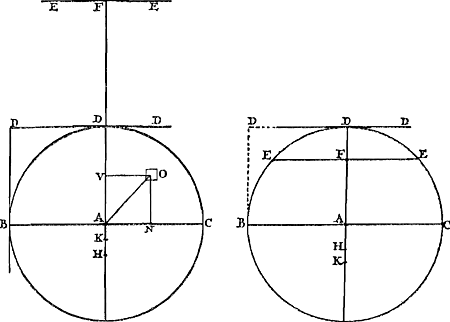 [Fig. 95].Ga naar margenoot+
figura BCD circa axem EF [Fig. 95]; hic, si cuneus super figura intelligatur abscissus, plano quod ita secet planum figurae, ut intersectio, quae hic est DD, sit parallela oscillationis axi; deturque distantia centri gravitatis figurae ab hac intersectione, ut hic AD; itemque subcentrica cunei dicti super eadem intersectione, quae hic sit DH. Habebitur centrum oscillationis K, figurae BDC, applicando rectangulum DAH ad distantiam FA; quoniam ex applicatione hac orietur distantia AK, qua centrum oscillationis inferius est centro gravitatis. Est enim rectangulum DAH, multiplex secundum numerum particularum figurae BCD, aequale quadratis distantiarum ab recta BAC, quae per centrum gravi|tatis A parallela ducitur axi oscillationis EFGa naar margenoot*. Quare,Ga naar margenoot+ applicando idem rectangulum ad distantiam FA, orietur distantia AK, qua centrum oscillationis inferius est centro gravitatis AGa naar margenoot*. Hinc manifestum est, si axis oscillationis sit DD, fieri centrum oscillationis H punctum, adeoque longitudinem DH, penduli simplicis isochroni figurae BCD, esse tunc ipsam subcentricam cunei, abscissi plano per DD, super ipsam DD. Quod unum ab aliis ante animadversum fuit, non tamen demonstratumGa naar voetnoot1). Quomodo autem centra gravitatis cuneorum super figuris planis inveniantur, persequi non est instituti nostri, & jam in multis nota sunt. Velut, quod si figura BCD sit circulus, erit DH aequalis ⅝ diametri. Si rectangulum, erit DH ∞ ⅔ diametri. Unde & ratio apparet cur virga, seu linea gravitate praedita, altero capite suspensa, isochrona sit pendulo longitudinis subsesquialterae. Considerando nempe lineam ejusmodi, ac si esset rectangulum minimae latitudinis. | |||||||||||||||||||||||||||||||||||
[pagina 308]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Que si la figure est un triangle dont le sommet est tourné vers le haut, on trouve DH = ¾ du diamètre; s'il est tourné vers le bas, DH = la moitié du diamètre. Il faut savoir en outre que ce qui a été démontré dans la Prop. XVI s'applique de la façon suivante au mouvement considéré de la figure plane: si nous donnons à la figure BCD toutes sortes de positions différentes, la faisant tourner autour de l'axe BAC du manière à lui donner une position horizontale ou oblique, tandis que l'axe d'oscillation FE demeure le même, la longueur FK du pendule isochrone sera également invariable. Voilà ce que cette proposition nous enseigne. Considérons en second lieu le mouvement oscillatoire d'une figure plane autour d'un axe perpendiculaire au plan de la figure, ce que nous avons appelé oscillation latérale; par exemple celle de la figure BCD [Fig. 96] autour d'un axe passant par le point F normalement au plan DBC. Dans ce cas il faut prendre en considération, outre l'onglet coupé sur la figure par un plan passant par DD, tangente à la figure en son plus haut point, un deuxième onglet coupé par un plan passant par BD, tangente latérale à la figure et perpendiculaire à la tangente DDGa naar voetnoot1). Et il faut qu'outre le centre de gravité A de la figure et la subcentrique HD du premier onglet, la subcentrique LB du deuxième onglet soit également connue. En effet, de cette façon on connaîtra les rectangles DAH et BAL dont la somme, que dans la suite nous appellerons aussi le Rectangle d'oscillation, constitue l'espace qui, divisé par la distance FA, donnera la distance AK de laquelle le centre d'oscillation K est inférieur au centre de gravité A. | |||||||||||||||||||||||||||||||||||
[pagina 309]
| |||||||||||||||||||||||||||||||||||
Quod si figura triangulum fuerit, vertice sursum converso, sit DH ¾ diametri. SiGa naar margenoot+ deorsum, ½ diametri. Quod autem propositione 16 demonstratum fuit, id ad hujusmodi figurae planae motum ita pertinere sciendum. Nempe, si aliam atque aliam positionem demus figurae BCD, invertendo eam circa axem BAC, ut vel horizonti parallela jaceat, vel oblique inclinetur, manente eodem agitationis axe FE, etiam longitudo penduli isochroni FK eadem manebit. Hoc enim ex propositione illa manifestum est. 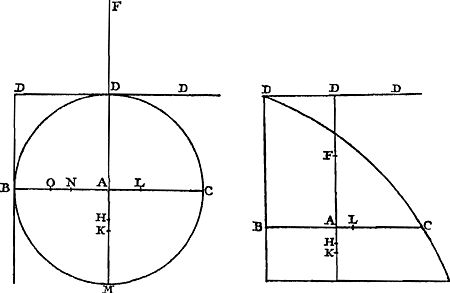 [Fig. 96.]
Porro quando figura plana, circa axem ad planum figurae erectum, agitatur; quam vocavimus agitationem in latus; velut si figura BCD [Fig. 96] moveatur circa axem, qui per punctum F intelligitur ad planum DHC erectus; hic jamGa naar voetnoot1) praeter cuneum super figura, qui abscinditur plano ducto per DD, tangentem figuram in puncto summo, alter quoque considerandus cuneus qui abscinditur plano per BD tangentem figuram in latere, quaeque tangenti DD sit ad rectos angulos. Oportetque dariGa naar voetnoot1), praeter figurae centrum gravitatis A, subcentricamque HD cunei prioris, etiam subcentricam LB cunei posterioris. Ita enim nota erunt rectangula DAH, BAL, quae simul sumpta faciunt hic spatium applicandum, quod deinceps etiam rectangulum oscillationis vocabitur. Quod nempe, applicatum ad distantiam FA, dabit distantiam AK, qua centrum oscillationis K inferius est centro gravitatis A. | |||||||||||||||||||||||||||||||||||
[pagina 310]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Mais si FA est un axe de la figure BCD [Fig. 96, I] on pourra, au lieu de l'onglet coupé par BD sur la figure entière, se servir d'un onglet coupé sur la demi-figure DBM par un plan passant par DM. Car si OA est la subcentrique par rapport à DM de cet onglet et NA la distance à la même droite DM du centre de gravité de la figure plane DBM, il appert que le rectangle OAN est égal au rectangle BALGa naar margenoot*. De cette façon la somme des rectangles OAN et DAH sera aussi le plan qu'il faut diviser par la distance FA pour obtenir la distance AK. La démonstration de ces dernières choses est manifeste par les précédentes, puisque les rectangles DAH et BAL ou DAH et OAN, multipliés par le nombre des particules de la figure, sont égaux aux carrés des distances au centre de gravité A, ou bien, ce qui est ici la même chose, aux carrés des distances à un axe de gravité parallèle à l'axe d'oscillation, et que par conséquent le quotient des rectangles susdits par la distance FA nous donne la longueur de l'intervalle AKGa naar margenoot*. | |||||||||||||||||||||||||||||||||||
Centre d'oscillation du cercle.Or, dans le cas du cercle [Fig. 96] il est évident que les rectangles DAH et BAL sont égaux entre eux et que leur somme constitue la moitié du carré du rayon. Par conséquent si, comme FA est au rayon AB, ainsi ce dernier est dit se rapporter à une autre longueur, la moitié de cette longueur-là sera la distance AK du centre de gravité au centre d'oscillation. Lorsque le cercle oscille autour de l'axe D pris sur la circonférence, DK sera donc égale aux trois quarts du diamètre DM. Suivant la même méthodeGa naar voetnoot1) nous avons aussi trouvé les centres d'oscillation dans le cas des figures planes suivantes; qu'il suffise de publier les résultats du calcul. | |||||||||||||||||||||||||||||||||||
Centre d'oscillation du rectangle.Dans tout rectangle tel que CB [Fig. 97] l'espace qui doit être divisé par une longueur, en d'autres termes le rectangle d'oscillation, est trouvé égal au tiers du carré de la demi-diagonale AC. Il s'ensuit que lorsque le rectangle est suspendu à un de ses angles et agité latéralement, le pendule qui lui est isochrone est égal à ⅔ de la diagonale entièreGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
Centre d'oscillation du triangle isoscèle.Dans le cas du triangle isoscèle, tel que CBD [Fig. 98], l'espace qui doit être divisé par une longueur est égal à la 18ième partie du carré du diamètre BE augmentée de la 24ième partie du carré de la base CD. | |||||||||||||||||||||||||||||||||||
[pagina 311]
| |||||||||||||||||||||||||||||||||||
Si vero FA sit axis figurae BCD [Fig. 96, I], potest, pro cuneo abscisso per | BDGa naar margenoot+ super figura tota, adhiberi cuneus super figura dimidia DBM abscissus plano per DM.Ga naar margenoot+ Nam, si cunei hujus subcentrica super DM sit OA, distantia vero centri gr. figurae planae DBM ab eadem DM sit NA, aequale esse constat rectangulum OAN rectangulo BALGa naar margenoot*. Itaque rectangulum OAN, additum rectangulo DAH, constituet quoque planum applicandum ad distantiam FA, ut fiat distantia AK. Et horum quidem manifesta est demonstratio ex praecedentibus, quippe cum rectangula DAH, BAL, vel DAH, OAN, multiplicia secundum numerum particularum figurae, aequalia sint quadratis distantiarum à centro gravitatis A; sive, quod idem hic est, ab axe gravitatis axi oscillationis parallelo; ac proinde rectangula dicta, ad distantiam FA applicata, efficiant longitudinem intervalli AKGa naar margenoot*. | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Circuli.Et in circulo quidem rectangula DAH, BAL, inter se aequalia esse liquet, simulque efficere semissem quadrati à semidiametro. Unde, si fiat ut FA ad semidiametrum AB, ita haec ad aliam, ejus dimidium erit distantia AK, à centro gravitatis ad centrum oscillationis. Si igitur circulus ab axe D, in circumferentia sumpto, agitetur, erit DK aequalis tribus quartis diametri DM. Ad hunc modumGa naar voetnoot1) & in sequentibus figuris planis centra oscillationis quaesivimus, quae simpliciter adscripsisse sufficiet. Nempe, | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Rectanguli.Ga naar margenoot+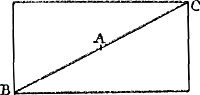 [Fig. 97.]
In rectangulo omni, ut CB [Fig. 97], spatium applicandum, sive rectangulum oscillationis, invenitur aequale tertiae parti quadrati à semidiagonio AC. Unde sequitur, si rectangulum ab aliquo angulorum suspendatur, motuque hoc laterali agitetur, pendulum illi isochronum esse ⅔ diagonii totiusGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
[pagina 312]
| |||||||||||||||||||||||||||||||||||
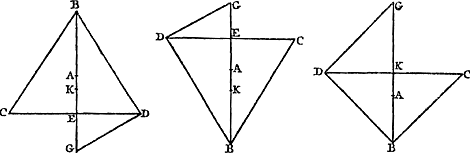
Ga naar margenoot+ [Fig. 98.]
Par conséquent, si à partir d'un angle de la base l'on tire DG perpendiculaire au côté DB et coupant en G le prolongement du diamètre BE, et que A est le centre de gravité du triangle, et si, après avoir divisé l'intervalle GA en quatre parties égales, on en ajoute une, savoir KA, à BA; BK sera la longueur du pendule isochrone, le triangle étant suspendu en son sommet B. Mais lorsqu'il est suspendu au point milieu E de la base, la longueur EK du pendule isochrone sera égale à la moitié de BG. Il en résulte que lorsqu'un triangle isoscèle rectangle est suspendu au point milieu de la base, il est isochrone avec un pendule ayant une longueur égale à son diamètre. Et que pareillement, lorsqu'il est suspendu à son angle droit, il est isochrone avec le même penduleGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Centre d'oscillation de la parabole.Dans le cas d'un segment de parabole limité par une droite perpendiculaire à l'axe, l'espace qu'il faut diviser par une droite est égal à 12/175 fois le carré de l'axe plus la cinquième partie du carré de la demi-base. Lorsque la parabole est suspendue à son sommet, on trouve pour la longueur du pendule isochrone une longueur de 5/7 fois l'axe + le tiers du latus rectum. Mais lorsqu'elle est suspendue au point milieu de la base, cette longueur sera de 4/7 sois l'axe plus la moitié du latus rectumGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
Centre d'oscillation du secteur de cercle.Si dans le secteur de cercle BCD [Fig. 99] le rayon BC est appelé r, le demi-arc CF p et la demi-corde CE b, l'espace qui doit être divisé par une droite devient égal à ½r2 - 4b2r2/9p2, c.à.d. à ½ BC2 - BA2, A étant par hypothèse le centre de gravité du secteur, car on a alors BA = 2br/3p. Le secteur étant suspendu en B, centre du cercle dont il fait partie, le pendule isochrone avec lui devient 3pr/4b, c.à.d. les trois quarts de la droite dont le rapport au rayon BF est égal à celui de l'arc CFD à la corde CD. | |||||||||||||||||||||||||||||||||||
[pagina 313]
| |||||||||||||||||||||||||||||||||||
Unde, si ab angulo baseos ducatur DG, perpendicularis super latus DB, quae occurratGa naar margenoot+ productae diametro BE in G; sitque A centrum gravitatis trianguli; divisoque intervallo GA in quatuor partes aequales, una earum AK apponatur ipsi BA; erit BK longitudo penduli isochroni, si triangulum suspendatur ex vertice B. Cum autem ex puncto mediae basis E suspenditur, longitudo penduli isochroni EK aequabitur dimidiae BG. Atque hinc liquet, triangulum isosceles rectangulum, si ex puncto mediae basis suspendatur, isochronum esse pendulo longitudinem diametro suae aequalem habenti. Similiterque, si suspendatur ab angulo suo recto, eidem pendulo isochronum esseGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Parabolae.In parabolae portione recta, spatium applicandum aequatur 12/175 quadrati axis, una cum quinta parte quadrati dimidiae basis. Cum|que parabola ex verticis puncto suspensaGa naar margenoot+ est, invenitur penduli isochroni longitudo 5/7 axis, atque insuper ⅓ lateris recti. Cum vero ex puncto mediae basis suspenditur, erit ea longitudo 4/7 axis, & insuper ½ lateris rectiGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Sectoris circuli.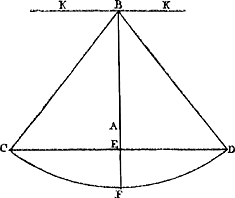 [Fig. 99.]
In circuli sectore BCD [Fig. 99], si radius BC vocetur r: semiarcus CF, p: semisubtensa CE, b: fit spatium applicandum aequale ½rr - 4bbrr/9pp, hoc est, dimidio quadrati BC, minus quadrato BA; ponendo A esse centrum gravitatis sectoris. Tunc enim BA ∞ 2br/3p. Si autem suspendatur sector ex B, centro circuli sui, fit pendulum ipsi isochronum 3pr/4b, hoc est, trium quartarum rectae, quae sit ad radium BF ut arcus CFD ad subtensam CD. Haec autem inveniuntur cognitis subcentricis cuneorum; | |||||||||||||||||||||||||||||||||||
[pagina 314]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ On obtient ces résultats lorsqu'on connaît les subcentriques des onglets, tant de celui qui est coupé sur le secteur total par un plan passant par BK parallèle à la corde CD (nous trouvons que la subcentrique par rapport à BK de cet onglet est 3r/8 - 3a/8 + 3pr/8b, en appelant a le sinus versus EF), que de celui qui est coupé sur le demi-secteur BFC par un plan passant par BF (nous trouvons que la subcentrique de cet onglet-là par rapport à BF est 3b/8 - 3br/8a + 3pr/8a)Ga naar voetnoot1). Mais on trouve aussi le centre d'oscillation du secteur d'après une autre méthode plus facile qui est la suivante. Soit le secteur BCP [Fig. 100], qui peut être considéré comme un triangle, une fort petite partie du secteur BCD. Or, les carrés des distances de ses particules au point B sont égaux aux carrés des distances à la droite BR qui divise le secteur en deux parties égales plus les carrés des distances à la droite BQ perpendiculaire à BR. Mais le rapport de ces derniers carrés aux premiers est supérieur à tout rapport donné, puisque l'angle CBP est extrêmement petit; par conséquent les premiers peuvent être considérés comme nuls. Prenons BO égale aux deux tiers de BR, ce qui revient à prendre O comme centre de gravité du triangle BCP, et BN égale aux trois quarts de BR, de sorte que N est le centre de gravité de l'onglet coupé sur le triangle BCP par un plan passant par BQ. Ceci étant posé, il apparaît que les carrés des distances des particules du triangle BCP à la droite BQ sont égaux au rectangle NBO multiplié par le nombre des particules du même triangle. Par conséquent le rectangle NBO multiplié par ce nombre doit être estimé égal aux carrés des distances au point B des particules du triangle BCP. Or, les carrés de ces distances sont aux carrés des distances du secteur entier BCD, comme le secteur BCP est au secteur BCD, en d'autres termes, comme le nombre des particules du secteur BCP est à celui des particules du secteur BCD: c'est ce qu'on comprend facilement en songeant que le secteur BCD peut être divisé en secteurs tels que BCP. Par conséquent le rectangle NBO, multiplié par le nombre des particules du secteur BCD, sera égal aux carrés des distances au point B de ces particules. Le rectangle NBO, divisé par BA qui est la distance du point de suspension au centre de gravité du secteur, donnera donc la longueur du pendule isochrone lorsque le secteur est suspendu en BGa naar margenoot*. Or, le rectangle NBO est égal à ½r2 et la distance BA, comme nous l'avons déjà dit auparavant, à 2br/3p. Par la division on obtient donc 3pr/4b pour la longueur du pendule isochrone, comme nous l'avions aussi trouvé plus haut. | |||||||||||||||||||||||||||||||||||
[pagina 315]
| |||||||||||||||||||||||||||||||||||
tum illius qui super sectore toto abscinditur, plano ducto per BK parallelam subtensaeGa naar margenoot+ CD, cujus cunei subcentricam super BK invenimus esse ⅜r - ⅜a + 3pr/8b, vocando a sinum versum EF; tum illius qui super dimidio sectore BFC abscinditur plano per BF, cujus nempe cunei subcentricam super BF invenimus ⅜b - 3br/8a + 3pr/8aGa naar voetnoot1). 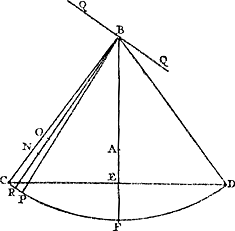 [Fig. 100.]
Sed & alia via, sectoris centrum oscillationis, facilius invenitur, quae est hujusmodi. Intelligatur sectoris BCD [Fig. 100] pars minima sector BCP, qui trianguli loco haberi potest. Quadrata autem, à distantiis particularum ejus à puncto B, aequalia sunt quadratis distantiarum ab recta BR, bifariam sectorem dividente, una cum quadratis distantiarum ab recta BQ, quae ipsi BR est ad angulos rectos. Sed, horum quadratorum ad illa, ratio quavis data est major, quoniam angulus CBP minimus; ideoque illa pro nullis habenda sunt. Positâ vero BO duarum tertiarumGa naar margenoot+ BR, hoc est, posito O centro gravitatis trianguli BCP; & BN trium quartarum BR: ut nempe N sit centrum gravitatis cunei, super trianguli BCP abscissi plano per BQ. His positis, constat quadrata, à distantiis particularum trianguli BCP ab recta BQ, aequari rectangulo NBO multiplici secundum particularum ejusdem trianguli numerum. Itaque rectangulum NBO, ita multiplex, aequale censendum quadratis distantiarum à puncto B particularum trianguli BCP. Sunt autem quadrata distantiarum harum, ad quadrata distantiarum totius sectoris BCD, sicut sector BCP ad sectorem BCD, hoc est, sicut numerus particularum sectoris BCP, ad numerum particularum sectoris BCD; hoc enim facile intelligitur, eo quod sector BCD dividatur in sectores qualis BCP. Ergo rectangulum NBO, multiplex secundum numerum particularum sectoris BCD, aequale erit quadratis distantiarum particularum ejus à puncto B. Ideoque rectangulum NBO, applicatum ad BA, distantiam inter suspensionem & centrum gravitatis sectoris, dabit longitudinem penduli isochroni, cum sector ex B suspenditurGa naar margenoot*. Est autem rectangulum NBO ∞ ½ rr: distantia autem BA, ut jam ante diximus, ∞ 2br/3p. Unde, facta applicatione, oritur 3pr/4b, longitudo penduli isochroni, ut ante quoque inventa fuit. | |||||||||||||||||||||||||||||||||||
[pagina 316]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Le Centre d'oscillation du cercle, autrement que ci-dessus.De la même manière on peut aussi trouver fort simplement le centre d'oscillation du cercle. Considérons en effet le cercle GCF à centre B [Fig. 101], et dans ce cercle le secteur extrêmement petit BCP, comme nous l'avons fait plus haut dans le cas du secteur BCD. Comme alors, suivant ce que nous venons d'exposer, les carrés des distances des particules du secteur BCP au centre B sont égaux au rectangle NBO, c.à.d. à la moitié du carré du rayon multiplié par le nombre des particules du secteur, et que le cercle est entièrement composé de secteurs de ce genre, il en résulte que les carrés des distances des particules du cercle entier au centre B seront égaux à la moitié du carré du rayon multiplié par le même nombre, celui des particules du cercle. Or, B est le centre de gravité du cercle. Par conséquent la dite moitié du carré du rayon sera ici l'espace qui doit être divisé par la distance du point de suspension au centre B pour obtenir l'intervalle dont le centre d'oscillation est inférieur au centre BGa naar margenoot*, ce qui s'accorde avec le résultat trouvé plus haut. | |||||||||||||||||||||||||||||||||||
Le Centre d'oscillation de la circonférence du cercle.Le centre d'oscillation de la circonférence de cercle est trouvé encore plus facilement par cette méthode. Considérons une circonférence décrite du centre B avec le rayon BR [Fig. 102]. Le carré de BR, multiplié par le nombre des particules dans lesquelles la circonférence peut être divisée par la pensée, est donc égal aux carrés des distances de toutes ces particules au centre B. BR2 sera par conséquent ici l'espace qu'il faut diviser par une droiteGa naar margenoot*. Et il ressort de là que lorsque la circonférence est suspendue au point G situé sur elle la longueur du pendule isochrone est égale au diamètre GFGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Le Centre d'oscillation des polygones réguliers.On trouve semblablement le pendule isochrone correspondant à un polygone ré- | |||||||||||||||||||||||||||||||||||
[pagina 317]
| |||||||||||||||||||||||||||||||||||
Centrum oscillationis Circuli, aliter quam supra.Ga naar margenoot+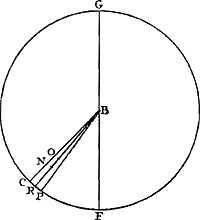 [Fig. 101.]
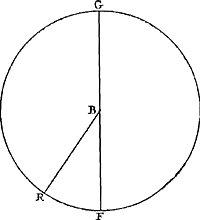 [Fig. 102.]
Eodem modo etiam simplicissime, in circulo, centrum oscillationis invenire licet. Sit enim circulus GCF, cujus centrum B [Fig. 101]; sectorque in eo minimus intelligatur BCP, sicut ante in sectore BCD. Cum igitur, secundum modo exposita, quadrata, à distantiis particularum sectorisGa naar margenoot+ BCP ad centrum B, aequentur rectangulo NBO, hoc est, dimidio quadrato radii, multiplici secundum sectoris ipsius particularum numerum; circulus autem ex ejusmodi sectoribus componatur; erunt proinde quadrata, à distantiis particularum circuli totius ad centrum B, aequalia dimidio quadrato radii, multiplici secundum numerum earundem circuli particularum. Est autem B centrum gravitatis circuli. Ergo dictum dimidium quadratum radii, hic erit spatium applicandum distantiae inter suspensionem & centrum B, ut habeatur intervallum, quo centrum oscillationis inferius est ipso centro BGa naar margenoot*. quod & supra ita se habere ostendimus. | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Peripheriae circuli.Facilius etiam, centrum oscillationis circumferentiae circuli, hoc | pacto reperitur.Ga naar margenoot+ Esto enim circumferentia descripta centro B, radio BR [Fig. 102]. Quadratum igitur BR, multiplex secundum numerum particularum in quas circumferentia divisa intelligitur, aequatur quadratis à distantiis omnium earum particularum ad centrum B. Quare quadratum BR erit hic spatium applicandumGa naar margenoot*. Patetque hinc, si suspensio sit ex G, puncto circumferentiae, penduli isochroni longitudinem aequari diametro GFGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
[pagina 318]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ gulier quelconque tel que ABC [Fig. 103]. En effet, l'espace qu'il faut diviser par une droite devient égal à la moitié du carré de la perpendiculaire abaissée du centre sur le côté du polygone plus la vingt-quatrième partie du carré du côté. Mais si l'on cherche le pendule isochrone avec le périmètre du polygone, l'espace qu'il faut diviser par une droite devient égal au carré de la perpendiculaire du centre sur le côté augmenté de la douzième partie du carré du côtéGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Usage du lieu plan et du lieu solide dans cette théorie.Outre cela la contemplation des lieux n'est pas désagréable en ces choses. Qu'on demande par exemple, étant donné le point de suspension A et la longueur AB [Fig. 104], de trouver le lieu de deux poids égaux C, D, également distants de A et de la perpendiculaire AB, qui soient isochrones, en oscillant autour de l'axe A perpendiculaire au plan passant par ACD, avec le pendule simple de longueur AB. Posons AB = a, et après que nous avons tiré CD coupant AB en E à angles droits, soit AE, grandeur indéterminée, = x et EC ou ED = y. Par conséquent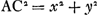 . Or, cette expression, multipliée par le nombre des particules des poids C et D, qui sont considérés ici comme extrêmement petits, est égale aux carrés des distances de ces mêmes particules de l'axe de suspension A. La division de AC2 ou x2 + y2 par la distance AE de l'axe de suspension au centre de gravité des poids C, D, donnera donc la longueur . Or, cette expression, multipliée par le nombre des particules des poids C et D, qui sont considérés ici comme extrêmement petits, est égale aux carrés des distances de ces mêmes particules de l'axe de suspension A. La division de AC2 ou x2 + y2 par la distance AE de l'axe de suspension au centre de gravité des poids C, D, donnera donc la longueur 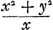 du pendule isochroneGa naar margenoot*, qui par hypothèse doit être égale à AB ou a. Donc du pendule isochroneGa naar margenoot*, qui par hypothèse doit être égale à AB ou a. Donc 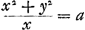 , et , et 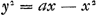 . D'où il apparaît que le lieu des points C et D est une circonférence de cercle dont le centre F est situé au milieu de AB et dont le rayon est ½ a ou FA. Par conséquent, en quelques points de la circonférence ACBD que deux poids égaux également distants de A soient placés, ils seront isochrones, en oscillant autour de A, avec un pendule ayant une longueur égale au diamètre ABGa naar voetnoot2). . D'où il apparaît que le lieu des points C et D est une circonférence de cercle dont le centre F est situé au milieu de AB et dont le rayon est ½ a ou FA. Par conséquent, en quelques points de la circonférence ACBD que deux poids égaux également distants de A soient placés, ils seront isochrones, en oscillant autour de A, avec un pendule ayant une longueur égale au diamètre ABGa naar voetnoot2).
Il est encore manifeste par là que la circonférence ACBD, supposée pesante, et | |||||||||||||||||||||||||||||||||||
[pagina 319]
| |||||||||||||||||||||||||||||||||||
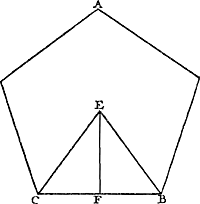 [Fig. 103.]
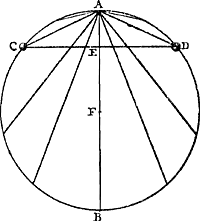 [Fig. 104.]Ga naar margenoot+
chronum invenitur. Fit enim, spatium applicandum, aequale semissi quadrati perpendicularis ex centro in latus polygoni, una cum vigesima quarta parte quadrati lateris. At, si perimetro polygoni pendulum isochronum quaeratur, fit spatium applicandumaequale quadrato perpendicularis à centro in latus, cum duodecima parte quadratilaterisGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Loci plani & solidi usus in hac Theoria.Est praeterea & Locorum contemplatio in his non injucunda. Ut si propositum sit, dato puncto suspensionis A, & longitudine AB [Fig. 104], invenire locum duorum ponderum aequalium C, D, aequaliter ab A & à perpendiculari AB distantium, quae agitata circa axem in A, perpendicularem plano per ACD, isochrona sint pendulo simplici longitudinis AB. Ponatur AB ∞ a, ductâque CD, quae secet AB ad angulos rectos in E, sit AE indeterminata ∞ x: EC vel ED ∞ y. Ergo quadratum AC ∞ xx + yy. Hoc vero multiplex secundum numerum particularum ponderum C, D, quae hic minima intelliguntur, aequatur quadratis distantiarum earundem particularum ab axe | suspensionisGa naar margenoot+ A. Ergo quadratum AC, sive xx + yy, applicatum ad distantiam AE, quae nempe est inter axem suspensionis & centrum gravitatis ponderum C, D, efficiet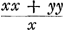 , longitudinem penduli isochroniGa naar margenoot*; quam propterea oportet aequalem esse AB sive a. Itaque , longitudinem penduli isochroniGa naar margenoot*; quam propterea oportet aequalem esse AB sive a. Itaque 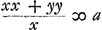 . Et yy ∞ ax - xx. Unde patet, locum punctorum C & D, esse circumferentiam circuli, cujus centrum F, ubi AB bifariam dividitur, radius autem ∞ ½a, sive FA. Ergo, ubicunque in circumferentia ACBD duo pondera aequalia, aequaliter ab A distantia, ponentur, ea, ex A agitata, isochrona erunt pendulo longitudinem habenti aequalem diametro ABGa naar voetnoot2). . Et yy ∞ ax - xx. Unde patet, locum punctorum C & D, esse circumferentiam circuli, cujus centrum F, ubi AB bifariam dividitur, radius autem ∞ ½a, sive FA. Ergo, ubicunque in circumferentia ACBD duo pondera aequalia, aequaliter ab A distantia, ponentur, ea, ex A agitata, isochrona erunt pendulo longitudinem habenti aequalem diametro ABGa naar voetnoot2).
Atque hinc manifestum quoque, & circumferentiam ACBD, si gravitas ei tribuatur, | |||||||||||||||||||||||||||||||||||
[pagina 320]
| |||||||||||||||||||||||||||||||||||
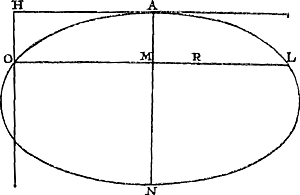
Ga naar margenoot+ [Fig. 105.]
une portion quelconque d'elle divisée en deux parties égales par le point A ou B, est isochrone avec le même pendule AB lorsqu'elle est suspendue à l'axe passant par AGa naar voetnoot1).
Donnons maintenant un exemple d'un lieu solide. Soit AN [Fig. 105] une ligne inflexible et impondérable et qu'on demande d'attacher à elle à angles droits en un point pris sur elle tel que M une ligne ou verge pondérable OML divisée en deux parties égales par le point M, dont les oscillations latérales, A étant le point de suspension, soient isochrones avec un pendule simple de longueur AN. Tirons OH parallèlement à AN, et AH parallèlement à OM; et soit OR = ⅔ OL. OR sera par conséquent la subcentrique de l'onglet coupé sur la droite OL par un plan passant par OH. Mais la subcentrique du second onglet coupé sur la même droite OL par un plan passant par la droite AH (onglet qui n'est autre chose qu'un rectangle) sera la droite AN. Par conséquent le rectangle que nous avons appelé plus haut rectangle d'oscillation, sera seulement le rectangle OMR. Celui-ci, divisé par la longueur AM, donnera la distance de laquelle le centre d'oscillation de la ligne OL suspendue en A est inférieur au point M. Soit maintenant AN = a, AM = x, MO ou ML = y. Le rectangle OMR est donc égal à ⅓ y2. La division de cette expression par AM donne ⅓ y2/x. Cette longueur devra donc être égale à MN, puifque nous voulons que le centre d'oscillation de la verge OL soit en N. L'équation devient donc égale à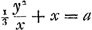 . D'où l'on tire . D'où l'on tire
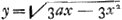 . Ce qui signifie que les points O et L se trouvent sur une ellipse dont AN est le petit axe, tandis que le latus rectum par rapport aux ordonnées perpendiculaires à l'axe est le triple de AN. . Ce qui signifie que les points O et L se trouvent sur une ellipse dont AN est le petit axe, tandis que le latus rectum par rapport aux ordonnées perpendiculaires à l'axe est le triple de AN.
Il en résulte manifestement, puisque toute verge parallèle à OL et ayant ses extrémités sur cette ellipse exécute des oscillations isochrones avec le pendule simple AN, que le plan entier de l'ellipse suspendu en A et oscillant latéralement sera également isochrone avec le pendule AN. Et il en sera de même pour une partie de l'ellipse limitée par une ou deux perpendiculaires à ANGa naar voetnoot2).
Nous ajouterons encore un deuxième exemple d'un lieu plan dans lequel se rencontrent quelques choses dignes d'être remarquées. | |||||||||||||||||||||||||||||||||||
[pagina 321]
| |||||||||||||||||||||||||||||||||||
& quamlibet ejus portionem, aequaliter in A vel B divisam, & ab axe per A suspensam,Ga naar margenoot+ eidem pendulo AB isochronam esseGa naar voetnoot1).
Loci vero solidi exemplum esto hujusmodi. Sit AN [Fig. 105] linea inflexilis sine pondere. Propositumque sit, ad punctum in ea acceptum, ut M, affigere ipsi ad angulos rectos lineam, seu virgam, pondere praeditam OML, ad M bifariam divisam, cujus in latus agitatae oscillationes, ex suspensione A, isochronae sint pendulo simplici longitudinis AN. Ducatur OH parallela AN, & AH parallela OM, & sit OR aequalis ⅔ OL. Itaque cunei super recta OL, abscissi plano per OH ducto, subcentrica erit OR. Sed cunei alterius super eadem OL, abscissi plano per rectam AH, (est autem cuneus hic nihil aliud quam rectangulum) subcentrica erit ipsa AM. Quare rectangulum illud, quod supra Oscillationis vocavimus, erit solum rectangulum OMR. quod nempe, applicatum ad longitudinem AM, dabit distantiam centri oscillationis lineae OL, ex A suspensae, infra punctum M. Sit jam AN ∞ a: AM ∞ x: MO vel ML ∞ y. Est ergo rectangulum OMR ∞Ga naar margenoot+ ⅓ yy. quo applicato ad AM, sit 1yy/3x. quae longitudo itaque ipsi MN aequalis esse debebit, cum velimus centrum oscillationis virgae OL esse in N. Fit ergo aequatio 1yy/3x + x ∞ a. Unde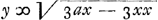 . Quod significat puncta O & L esse ad Ellipsin, cujus axis minor AN; latus rectum vero, secundum quod possunt ordinatim ad axem hunc applicatae, ipsius AN triplum.
Hinc vero manifestum fit, cum omnis virga ipsi OL parallela, & ad Ellipsin hanc . Quod significat puncta O & L esse ad Ellipsin, cujus axis minor AN; latus rectum vero, secundum quod possunt ordinatim ad axem hunc applicatae, ipsius AN triplum.
Hinc vero manifestum fit, cum omnis virga ipsi OL parallela, & ad Ellipsin hanc
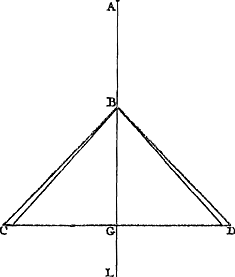 terminata, oscillationes isochronas habeat pendulo simplici AN, etiam totum Ellipseos planum, ex A suspensum & in latus agitatum, ipsi AN pendulo isochronum fore. Sed & partem Ellipseos quamlibet, quae lineis una vel duabus, ad AN perpendicularibus, abscindeturGa naar voetnoot2).
terminata, oscillationes isochronas habeat pendulo simplici AN, etiam totum Ellipseos planum, ex A suspensum & in latus agitatum, ipsi AN pendulo isochronum fore. Sed & partem Ellipseos quamlibet, quae lineis una vel duabus, ad AN perpendicularibus, abscindeturGa naar voetnoot2).
Caeterum adscribemus & aliud loci plani exemplum, in quo nonnulla notatu digna occurrunt. | |||||||||||||||||||||||||||||||||||
[pagina 322]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Soit suspendue en A la verge impondérable AB [Fig. 106] et qu'on demande d'attacher à un point B donné sur elle deux triangles égaux et écartés d'un même angle de l'axe AB, tels que leurs angles auprès de B étant considérés comme extrêmement ou plutôt infiniment petits ils exécutent des oscillations isochrones avec un pendule simple de longueur donnée ALGa naar voetnoot1). On trouve dans ce cas, après avoir tiré CG perpendiculairement à BG et posé AB = a, AL = b, BG = x, CG = y, l'équation 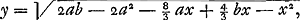 d'où il ressort que les bases C et D des triangles considérées ici comme punctiformes se trouvent sur une circonférence de cercle [Fig. 107], puisque la formule contient le terme sans facteur - xx. Or, on peut observer dans ce cas que si a = o, c.à.d. si le point où les triangles BC et BD sont attachés est le point A lui-même, l'équation sera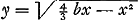 . Par conséquent, si l'on prend alors AO = ⅔ b, c.à.d. ⅔ AL, et qu'on décrit du centre O par A le cercle ADN, les bases des triangles AC et AD seront situées sur sa circonférence. Comme une paire de triangles fort aigus ayant leur sommet commun au point A de la circonférence ACND, égaux et symétriquement placés, a donc son centre d'oscillation au point L, en prenant AL = ¾ du diamètre AN, et comme le cercle entier est composé de pareilles paires de triangles, et qu'il en est de même pour une portion quelconque ACND du cercle, ayant ses côtés AC et AD égaux, il est manifeste que L sera le centre d'oscillation tant du cercle entier que d'une portion de ce genre.
Derechef, si dans l'équation trouvée on pose 8/3 a = 4/3 b ou 2a = b, c.à.d. si l'on suppose les triangles suspendus en B qui divise la longueur AL en deux parties égales [Fig. 108] en aura . Par conséquent, si l'on prend alors AO = ⅔ b, c.à.d. ⅔ AL, et qu'on décrit du centre O par A le cercle ADN, les bases des triangles AC et AD seront situées sur sa circonférence. Comme une paire de triangles fort aigus ayant leur sommet commun au point A de la circonférence ACND, égaux et symétriquement placés, a donc son centre d'oscillation au point L, en prenant AL = ¾ du diamètre AN, et comme le cercle entier est composé de pareilles paires de triangles, et qu'il en est de même pour une portion quelconque ACND du cercle, ayant ses côtés AC et AD égaux, il est manifeste que L sera le centre d'oscillation tant du cercle entier que d'une portion de ce genre.
Derechef, si dans l'équation trouvée on pose 8/3 a = 4/3 b ou 2a = b, c.à.d. si l'on suppose les triangles suspendus en B qui divise la longueur AL en deux parties égales [Fig. 108] en aura
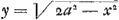 , équation qui fait voir que si du centre B avec un rayon dont le carré est égal à 2BA2 on décrit une circonférence, celle-ci sera le lieu des bases des triangles infiniment aigus BC et BD, desquels, lorsqu'ils sont sus pendus en A, L sera donc le centre d'oscillation. Et comme le cerc le entier ainsi qu'un quelconque de ses secteurs ayant son axe sur la droite AL est composé de pa reilles paires de triangles, il est manifeste que toutes ces figures, suspendues en A, auront aussi leur centre d'oscillation au point L. , équation qui fait voir que si du centre B avec un rayon dont le carré est égal à 2BA2 on décrit une circonférence, celle-ci sera le lieu des bases des triangles infiniment aigus BC et BD, desquels, lorsqu'ils sont sus pendus en A, L sera donc le centre d'oscillation. Et comme le cerc le entier ainsi qu'un quelconque de ses secteurs ayant son axe sur la droite AL est composé de pa reilles paires de triangles, il est manifeste que toutes ces figures, suspendues en A, auront aussi leur centre d'oscillation au point L.
| |||||||||||||||||||||||||||||||||||
[pagina 323]
| |||||||||||||||||||||||||||||||||||
Sit virga AB ponderis expers, suspensa ex A [Fig. 106]; oporteatque, ad da|tum inGa naar margenoot+ ea punctum B, affigere triangula duo paria, & paribus angulis ab axe AB recedentia,Ga naar margenoot+ quorum anguli ad B minimi, sive infinite parvi existimandi, quaeque, ita suspensa ab A, oscillationes isochronas faciant pendulo simplici datae longitudinis ALGa naar voetnoot1). 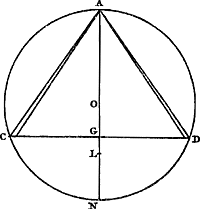 [Fig. 107.]
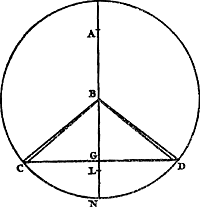 [Fig. 108.]
Hic, ducta CG perpendiculari in BG, & ponendo AB ∞ a; AL ∞ b; BG ∞ x; CG ∞ y: invenitur aequatio 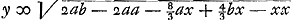 . ex qua patet, bases triangulorum C, & D, quae bases hic ut puncta considerantur, esse ad circuli circumferentiam [Fig. 107]; quia nempe habetur terminus simplex - xx.
Licet autem hic animadvertere, quod si a sit nihilo aequalis, hoc est, si punctum, ubi affiguntur trianguli BC, BD, sit idem cum puncto A; tum futura sit aequatio . ex qua patet, bases triangulorum C, & D, quae bases hic ut puncta considerantur, esse ad circuli circumferentiam [Fig. 107]; quia nempe habetur terminus simplex - xx.
Licet autem hic animadvertere, quod si a sit nihilo aequalis, hoc est, si punctum, ubi affiguntur trianguli BC, BD, sit idem cum puncto A; tum futura sit aequatio
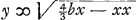 . Ac proinde, hoc casu, si sumatur AO ∞ ⅔ b, hoc est, ∞ ⅔ AL, centroque O per A circulus describatur ADN; erunt bases triangulorum AC, AD, ad illius circumferentiam. Cum igitur quaelibet duo triangula acutissima, quae ex A ad circumferentiam ACND constituuntur, magnitudine & situ sibi respondentia, centrum oscillationis habeant punctum L, positâ AL ∞ ¾ diametri AN; cumque circulus totus ex cujusmodi triangulorum paribus componatur; uti & portio ejus quaelibet, ut ACND, latera AC, AD aequalia habens; manifestum est, tum circuli totius, tum portionis qualem diximus, centrum oscillationis esse in L.
Rursus, si in aequatione inventa ponatur 8/3 a ∞ 4/3 b, seu 2 a ∞ b; hoc est, si triangula affigi intelligantur in B, quod longitudinem AL secet bifariam [Fig. 108], erit . Ac proinde, hoc casu, si sumatur AO ∞ ⅔ b, hoc est, ∞ ⅔ AL, centroque O per A circulus describatur ADN; erunt bases triangulorum AC, AD, ad illius circumferentiam. Cum igitur quaelibet duo triangula acutissima, quae ex A ad circumferentiam ACND constituuntur, magnitudine & situ sibi respondentia, centrum oscillationis habeant punctum L, positâ AL ∞ ¾ diametri AN; cumque circulus totus ex cujusmodi triangulorum paribus componatur; uti & portio ejus quaelibet, ut ACND, latera AC, AD aequalia habens; manifestum est, tum circuli totius, tum portionis qualem diximus, centrum oscillationis esse in L.
Rursus, si in aequatione inventa ponatur 8/3 a ∞ 4/3 b, seu 2 a ∞ b; hoc est, si triangula affigi intelligantur in B, quod longitudinem AL secet bifariam [Fig. 108], erit
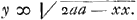 . quae aequatio docet, quod si centro B, radio qui possit duplum BA, circumferentia describatur, ea erit locus basium triangulorum acutissimorum BC, BD, | quorum nempe, ex A suspensorum, centrum oscillationis erit L punctum.Ga naar margenoot+ Cumque & circulus totus, & sector ejus quilibet, axem habens in recta AL, ex hujusmodi triangulorum paribus componatur, manifestum est & horum, ex A suspensorum, centrum oscillationis esse punctum L. . quae aequatio docet, quod si centro B, radio qui possit duplum BA, circumferentia describatur, ea erit locus basium triangulorum acutissimorum BC, BD, | quorum nempe, ex A suspensorum, centrum oscillationis erit L punctum.Ga naar margenoot+ Cumque & circulus totus, & sector ejus quilibet, axem habens in recta AL, ex hujusmodi triangulorum paribus componatur, manifestum est & horum, ex A suspensorum, centrum oscillationis esse punctum L.
| |||||||||||||||||||||||||||||||||||
[pagina 324]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Conséquemment un secteur de cercle quelconque, suspendu en un point distant du centre de son cercle d'une longueur égale à la moitié du côté du carré inscrit à ce cercle, aura un pendule isochrone égal en longueur à ce côté entier. Et ainsi, dans ce seul cas, en trouve un pendule isochrone avec le secteur indépendamment de la dimension de son arc. Enfin, lorsqu'il s'agit de la construction universelle de la première équation 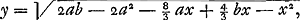 il faut diviser AL [Fig. 109] en deux parties égales en E, et ajouter à BE sa tierce partie EF; alors F sera le centre du cercle que l'on doit décrire en prenant un rayon FO, dont le carré est égal à 2(AE2 - EF2). Si l'on prend alors une paire de triangles infiniment aigus, tels que BC et BD, ayant leur sommet commun en B, leur centre d'oscillation, lorsqu'ils sont suspendus en A, sera L. Et il est manifeste que L sera également centre d'oscillation d'une portion quelconque du cercle décrit ayant son sommet en B et son axe sur la droite AL, telle que l'ensemble des deux figures CBD, la suspension étant toujours en A. Ceci s'applique aussi aux segments de cercle KON et KMN limités par la droite KBN perpendiculaire à AB.
Qu'il suffise d'avoir remarqué ces choses du mouvement latéral des plans et des lignes. Nous y ajoutons seulement encore ceci que lorsqu'on a trouvé les centres d'oscillation des figures droites, c.à.d. symétriques par rapport à l'axe, comme du triangle isoscèle ou du segment droit de parabole, on connaît également ceux des figures obliques provenant des figures droites pour ainsi dire par luxation, comme il en est du triangle scalène et du segment oblique de la parabole. Comme par exemple, lorsqu'on suppose le triangle isoscèle BAC à axe AD suspendu au point E [Fig. 110], et qu'on considère en outre le triangle scalène FAG ayant le même axe AD et une base FG égale à la base BC, je dis que ce triangle-là, suspendu en E, est isochrone avec le premier BAC. En effet, comme une verge ou ligne pesante FG, attachée en D à une verge im- | |||||||||||||||||||||||||||||||||||
[pagina 325]
| |||||||||||||||||||||||||||||||||||
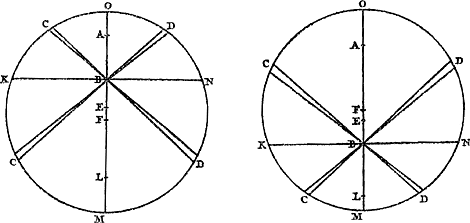 [Fig. 109.]Ga naar margenoot+
Adeoque quilibet circuli sector, suspensus à puncto quod distet, à centro circuli sui, semisse lateris quadrati circulo inscripti, pendulum isochronum habebit toti eidem lateri aequale. Atque ita, hoc uno casu, absque posita dimensione arcus, pendulum sectori isochronum invenitur. Porro, ad universalem constructionem aequationis primae,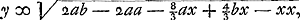 dividatur AL [Fig. 109] bifariam in E, & adponatur ad BE pars sui tertia EF; eritque F centrum describendi circuli; radius autem FO aequalis sumendus ei, quae potest duplum differentiae quadratorum AE, EF.
dividatur AL [Fig. 109] bifariam in E, & adponatur ad BE pars sui tertia EF; eritque F centrum describendi circuli; radius autem FO aequalis sumendus ei, quae potest duplum differentiae quadratorum AE, EF.
Si itaque, ex puncto B, ad descriptam circumferentiam triangula duo paria acutissima constituantur, ut BC, BD; illorum, ex A | suspensorum, centrum oscillationis erit L. Quare & portionis cujuslibet descripti circuli, cujus portionis vertex sit in B,Ga naar margenoot+ axis vero in recta AL, quales sunt utraque CBD; posita suspensione ex A; centrum oscillationis idem punctum L esse constat. Atque adeo etiam circuli segmentorum KON, KMN, quae facit recta KBN perpendicularis ad AB.
Et haec quidem de motu laterali planorum, ac linearum, animadvertisse sufficiat. Quibus hoc tantum addimus; inventis centris oscillationis figuram rectarum, seu quae aequaliter ad axem utrinque constitutae sunt; ut trianguli isoscelis, vel parabolicae sectionis rectae; etiam obliquarum, quae velut luxatione illarum efficiuntur, ut trianguli scaleni, & parabolae non rectae, centra oscillationis haberi. Ut si, exempli gratia, triangulum BAC isosceles [Fig. 110], cujus axis AD, à puncto E suspensum intelligatur; sit vero & aliud triangulum scalenum FAG, axem eundem habens AD, & basin FG aequalem basi BC; etiam hoc triangulum, ex E suspensum, priori BAC isochronum esse dico. Quia enim virga, seu linea gravis, FG, affixa virgae sine pondere ED in D, situ | |||||||||||||||||||||||||||||||||||
[pagina 326]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ pondérable ED et suspendue obliquement au point E, est isochrone avec la verge BC attachée de la même manière en DGa naar margenoot*, et que la même chose est vraie pour les autres verges de chaque triangle qui coupent l'axe AD aux mêmes points et sont égales entre elles, il est nécessaire que les triangles entiers, lesquels peuvent être considérés comme composés de ces lignes ou verges, soient isochronesGa naar voetnoot1). Pour les autres figures la démonstration est semblable. | |||||||||||||||||||||||||||||||||||
Proposition XXII.Comment on trouve les centres d'oscillation dans les figures solides.Daus les corps solides aussi on trouvera facilement le centre d'oscillation à l'aide des théorèmes démontrés plus haut. En effet, si un corps ABC [Fig. 111] est suspendu à l'axe passant par le point E perpendiculairement à cette page et que le centre de gravité est F, qu'on mène par F les plans EFD, GFH dont le dernier est parallèle à l'horizon et dont l'autre passe par l'axe E et qu'on cherche d'après la Prop. XIV les sommes des carrés des distances des particules du corps ABC au plan GFH, et de même au plan EFD, c.à.d. deux rectangles qui, multipliés par le nombre des dites particules, sont égaux aux dites sommes. Ces rectangles divisés par la distance EF entre l'axe de suspension et le centre de gravité donneront l'intervalle FK duquel le centre d'agitation K est inférieur au centre de gravité F. Ceci est clair d'après la Prop. XVIII. Nous en donnerons aussi quelques exemples. | |||||||||||||||||||||||||||||||||||
Le centre d'oscillation de la pyramide.Soit d'abord [Fig. 112] une pyramide ABC à sommet A et axe AD, dont la base soit un carré de côté BC. Et supposons que ce corps oscille autour d'un axe passant par le sommet A perpendiculairement au plan de cette page. | |||||||||||||||||||||||||||||||||||
[pagina 327]
| |||||||||||||||||||||||||||||||||||
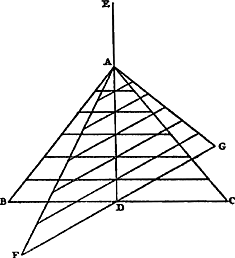 [Fig. 110.]
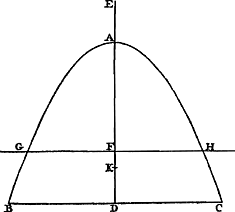 [Fig. 111.]Ga naar margenoot+
obliquo, suspensaque ex E, isochrona est virgae BC, similiter in D affixaeGa naar margenoot*; idemque evenit in virgis caeteris trianguli utriusque, quae axem AD secant in iisdem punctis, atque inter se aequales sunt: necesse est tota triangula, quae ex lineis, seu virgis iisdem composita intelligi possunt, isochrona esseGa naar voetnoot1). In aliis figuris similis est demonstratio. | |||||||||||||||||||||||||||||||||||
Propositio XXII.Ga naar margenoot+Quomodo, in solidis figuris, oscillationis centra inveniantur.In solidis porro figuris facile quoque, per ante demonstrata, centrum oscillationis invenire licebit. Si enim sit solidum ABC [Fig. 111], suspensum ab axe, qui, per punctum E, intelligitur hujus paginae plano ad rectos angulos; centrum autem gravitatis sit F: ductis jam per F planis EFD, GFH, quorum posterius sit horizonti parallelum, alterum vero per axem E transeat; inventisque, per propositionem 14, summis quadratorum à distantiis particularum solidi ABC à plano GFH, itemque à plano EFD; hoc est, inventis rectangulis utrisque, quae, multiplicia secundum numerum dictarum particularum, aequalia sint dictis quadratorum summis; rectangula haec applicata ad distantiam EF, qua nempe axis suspensionis distat à centro gravitatis, dabunt intervallum FK, quo centrum agitationis K inferius est centro gravitatis F. Hoc enim patet ex propositione 18. Dabimus autem & horum exempla aliquot. | |||||||||||||||||||||||||||||||||||
Centrum oscillationis in Pyramide.Sit primum ABC [Fig. 112] pyramis, verticem habens A, axem AD, basin vero quadratum, cujus latus BC. ponaturque agitari circa axem qui, per verticem A, sit hujus paginae plano ad angulos rectos. | |||||||||||||||||||||||||||||||||||
[pagina 328]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Ici la figure plane proportionnelle OVV qu'il faut placer à côté du corps d'après la Prop. XIV consistera en des résidus paraboliques OPV, c.à.d. en ce qui reste des rectangles ΩP lorsqu'on en ôte les demiparaboles OVΩ ayant leur sommet commun en O. En effet, comme sont entre elles les sections BC, NN de la pyramide, ainsi sont aussi entre elles les droites VV, RR qui leur correspondent dans la figure plane; et attendu que le centre de gravité E est situé du sommet de la pyramide à la distance de ¾ AD, le centre de gravité F de la figure OVV sera donc également distant du sommet O de trois quarts du diamètre OP. Considérons ensuite le plan horizontal NE passant par le centre de gravité de la pyramide ABC et coupant la figure OVV suivant RF, et cherchons la subcentrique OG de l'onglet coupé sur la figure OVV par un plan passant par OΩ (on trouve OG = ⅘ du diamètre OP); le rectangle OFG, multiplié par le nombre des particules de la figure OVV, sera égal aux carrés des distances à la droite RFGa naar margenoot* et par conséquent aussi aux carrés des distances au plan NE, des particules du corps ABC. Or, le rectangle OFG devient égal à 3/80 fois le carré OP ou AD. Ensuite, pour trouver la somme des distances au plan AD, il faut connaître d'abord la subcentrique de l'onglet coupé sur la base carrée de la pyramide BC par un plan passant par la droite en B parallèle à l'axe A. Soit BK cette subcentrique laquelle est égale à ⅔ BC. Il faut connaître de même la distance à OP du centre de gravité de la demi-figure OPV; soit cette distance ΦP laquelle est égale à 3/10 PV. Après cela, si l'on divise PV en deux parties égales en ∆ et que, comme ∆P est à PΦ, c.à.d. comme 5 est à 3, on prend le rectangle BDK, qui vaut 1/12 BC2, à un autre espace Z, ce dernier, multiplié par le nombre des particules du corps ABC, sera égal aux carrés des distances au plan ADGa naar margenoot*. Or, il apparaît que l'espace Z devient égal à 1/20 BC2. Il s'ensuit que l'espace entier qu'il faut diviser par une droite est égal ici à 3/80 AD2 + 1/20 BC2. Par conséquent, si la suspension est en A, sommet de la pyramide, comme nous l'avons supposé, et que la droite dont nous parlions est donc AE ou ¾AD, il en résultera que ES, intervalle dont le centre d'agitation est situé au-dessous du centre de gravité, est égal à 1/20 AD augmenté de 1/15 de la trosième proportionnelle à AD et BC. En d'autres termes la longueur AS entière sera égale à ⅘AD plus la dite quinzième partie de la troisième proportionnelle. | |||||||||||||||||||||||||||||||||||
[pagina 329]
| |||||||||||||||||||||||||||||||||||
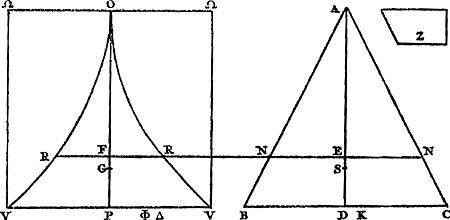 [Fig. 112.]Ga naar margenoot+
Hic figura plana proportionalis OVV, à latere adponenda, secundum propositionem 14, constabit ex residuis parabolicis OPV, quae nempe supersunt, cum, à rectangulis ΩP, auferuntur semiparabolae OVΩ, verticem habentes O. Sicut enim inter se sectiones pyramidis BC, NN, ita quoque rectae VV, RR, ipsisGa naar margenoot+ in figura plana respondentes. & sicut centrum gravitatis E distat, à vertice pyramidis, tribus quartis axis AD, ita quoque centrum gravitatis F, figurae OVV, distabit tribus quartis diametri OP à vertice O. Intellecto porro horizontali plano NE, per centrum gravitatis pyramidis ABC, quod idem figuram OVV secet secundum RE; inventâque subcentricâ cunei, super figura OVV abscissi plano per OΩ, quae subcentrica sit OG (est autem ⅘ diametri OP) erit rectangulum OFG, multiplex per numerum particularum figurae OVV, aequale quadratis distantiarum ab recta RFGa naar margenoot*, ac proinde quoque quadratis distantiarum à plano NE, particularum solidi ABC. Fit autem rectangulum OFG aequale 3/80 quadrati OP, vel quadrati AD. Deinde, ad inveniendam summam quadratorum à distantiis à plano AD, noscenda primo subcentrica cunei, super quadratâ basi pyramidis BC abscissi, plano per rectam quae in B intelligitur axi A parallela; quae subcentrica sit BK; estque ⅔BC. Noscenda item distantia centr. gr. dimidiae figurae OPV ab OP; quae sit ΦP; estque 3/10 PV. Inde, divisâ bifariam PV in ∆, si fiat ut ∆P ad PΦ, hoc est, ut 5 ad 3, ita rectangulum BDK, quod est 1/12 quadrati BC, ad aliud spatium Z; erit hoc, multiplex secundum numerum particularum solidi ABC, aequale quadratis distantiarum à plano ADGa naar margenoot*. Apparet autem fieri spatium Z aequale 1/20 quadrati BC. Itaque, totum spatium applicandum, aequatur hic 3/80 quadrati AD, cum 1/20 quadrati BC. Unde, si suspensio, ut hic, posita fuerit in A, vertice pyramidis, ideoque distantia, ad quam applicatio facienda, | AE aequalis ¼ AD; fiet hinc ES, intervallumGa naar margenoot+ quo centrum agitationis inferius est centro gravitatis, aequale 1/20 AD, atque insuper 1/15 tertiae proportionalis duabus AD, BC. sive tota AS aequalis ⅘ AD, praeter dictam 1/15 tertiae proportionalis. | |||||||||||||||||||||||||||||||||||
[pagina 330]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Le centre d'oscillation du cône.Que si ABC [Fig. 112] est un cône, toutes choses seront les mêmes à cela près qu'ici l'espace Z devient égal au rectangle ∆PΦGa naar margenoot*, c.à.d. à 3/20 PV2 ou 3/20 BD2, ou 3/80 BC2. C'est pourquoi l'espace entier qu'il faut diviser par une droite sera dans le cas du cône 3/80 AD2 + 3/80 BC2. Par conséquent, le sommet A étant par hypothèse le point de suspension, la longueur ES de laquelle le centre d'agitation est inférieur au centre de gravité, deviendra égale à 1/20 AD plus 1/20 de la troisième proportionnelle aux deux grandeurs AD et BC. En d'autres termes, la longueur AS entière deviendra égale à ⅘AD plus ⅕ de la troisième proportionnelle aux deux grandeurs AD et DBGa naar voetnoot1). Par là il est manifeste que si AD et DB sont égales, c.à.d. si le cône ABC est rectangle, AS devient égale à l'axe AD. Il résulte aussi de la Prop. XX que ce cône rectangle, si on le suspend au point D, centre de sa base, sera isochrone avec lui-même suspendu au sommet A, propriété analogue à celle du triangle rectangle, dont nous avons donné la démonstration cidessus. | |||||||||||||||||||||||||||||||||||
Le centre d'oscillation de la sphère.Si ABC [Fig. 113] est une sphère, la figure plane proportionnelle OVH qu'il faut placer à côté d'elle sera composée de paraboles dont la base commune OH est égale au diamètre AD de la sphère. La sphère étant coupée par des plans passant par le centre E, dont BC est un plan horizontal et AD un plan vertical, il faut connaître, pour qu'on puisse trouver la somme des carrés des distances au plan AD, la distance à OH du centre de gravité de la parabole OVH, laquelle soit ΦP. Sa longueur est de ⅖VP. Ensuite, PV étant divisée en deux parties égales en ∆, on sait que le rectangle ∆PΦ, multiplié par le nombre des particules de la sphère ABC, devient égal aux carrés des distances du plan ADGa naar margenoot*. Or, le rectangle ∆PΦ ést égal à ⅕PV2 ou ⅕BE2. | |||||||||||||||||||||||||||||||||||
[pagina 331]
| |||||||||||||||||||||||||||||||||||
Centrum oscillationis Coni.Quod si ABC [Fig. 112] conus fuerit, omnia eodem modo se habebunt, nisi quod spatium Z hic sit aequale rectangulo ∆PΦGa naar margenoot*, hoc est 3/20 quadrati PV vel BD, sive 3/80 quadrati BC. Quare, totum spatium applicandum, in cono erit 3/80 quadrati AD, una cum 3/80 quadrati BC. Ac proinde, posita suspensione ex vertice A, fiet ES, qua centrum agitationis inferius est centro gravitatis, aequalis 1/20 AD, & 1/20 tertiae proportionalis duabus AD, BC. sive tota AS aequalis ⅘AD, una cum ⅕ tertiae proportionalis duabus AD, DBGa naar voetnoot1). Atque hinc manifestum est, si AD, DB aequales sint, hoc est, si conus ABC sit rectangulus, fieri AS aequalem axi AD. Sequitur quoque porro, ex propositione 20, conum hunc rectangulum, si ex D centro baseos suspendatur, isochronum fore sibi ipsi ex vertice A suspenso, quemadmodum & de triangulo rectangulo supra ostensum fuit. | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Sphaerae.Sit ABC [Fig. 113] sit sphaera, erit figura plana proportionalis, à latere adponenda, OVH, ex parabolis composita, quarum basis communis OH, aequalis sphaerae diametro AD. Sectâ vero sphaerâ planis per centrum E, quorum BC sit horizonti parallelum, AD vero verticale: ut inveniatur summa quadratorum à distantiis à plano AD, noscenda est distantia centri gr. parabolae OVH ab OH, quae sit ΦP, estque ⅖VP. Deinde, divisâ PV bifariam in ∆, constat rectangulum ∆PΦ, multiplex per numerum particularum sphaerae ABC, aequari quadratis distantiarum à plano ADGa naar margenoot*. Est autem rectangulum ∆PΦ aequale ⅕ quadrati PV, vel quadrati BE. | |||||||||||||||||||||||||||||||||||
[pagina 332]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Or, il apparaît que les carrés des distances au plan BC sont égaux aux carrés des distances au plan AD, partant au même rectangle ∆PΦ multiplié par le dit nombre de particules. L'espace qu'il faut diviser par une droite sera donc, dans le cas de la sphère ABC, le double du rectangle ∆PΦ et par conséquent égal à ⅖EB2. Par conséquent, si la sphère est suspendue en un point A de sa surface, ES, distance de son centre E au centre d'agitation S, sera égale à ⅖ fois le rayon AE, et AS entière sera égale à 7/10 AD. Mais si la sphère est suspendue à un autre point tel que L, ES sera égale aux ⅖ d'une troisième proportionnelle aux deux grandeurs LE et EBGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Le centre d'oscillation du cylindre.Nous avons trouvé que dans le cylindre l'espace qu'il faut diviser par une droite est égale à 1/12 du carré de la hauteur augmenté d'un quart de la base. Il en résulte que lorsque le cylindre est suspendu au centre de sa base supérieure, la longueur du pendule isochrone devient égale aux ⅔ de son hauteur plus la moitié de la grandeur qui est au rayon de la base comme celui-ci est à la hauteur. | |||||||||||||||||||||||||||||||||||
Le centre d'oscillation du conoïde parabolique.Dans le conoïde parabolique le rectangle d'oscillation est 1/18 du carré de la hauteur augmenté de ⅙ du carré du rayon de la base. Par conséquent, si le conoïde est suspendu à son sommet, la longueur du pendule isochrone devient égal aux ¾ de l'axe, plus un quart d'une ligne qui est au rayon de la base comme celui-ci est à l'axe, c.à.d. plus ¼ du latus rectum de la parabole engendranteGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
Le centre d'oscillation du conoide hyperbolique.On peut aussi trouver le centre d'oscillation dans le conoïde hyperbolique. Si nous considérons par exemple le conoïde [Fig. 114] dont la section par l'axe est l'hyperbole BAB et qui a l'axe AD et le latus transversum AF, la figure plane qui lui est proportionnelle sera BKAKB, comprise entre la base BB et les arcs paraboliques symétriques AKB passant l'un et l'autre par le sommet A et ayant pour axe commun la ligne GE parallèle à la base BB et divisant en deux parties égales le latus transversum AF. Le centre de gravité L de cette figure BKAKB est donc à la même distance du sommet A que celui du conoïde ABB, et l'axe AD est à AL dans le rapport 3 FA + 2 AD : 2 FA + 3/2 AD. Ensuite on peut aussi trouver la distance à AD du centre de gravité de la demi-figure ADBK ainsi que la subcentrique par rapport à AP de l'onglet coupé sur la figure BKAKB par un plan passant per AP parallèle à BB; et de ces données on peut conclure à la situation du centre d'agitation du conoïde pour une suspension quelconque, pourvu que l'axe autour duquel le conoïde oscille soit paral- | |||||||||||||||||||||||||||||||||||
[pagina 333]
| |||||||||||||||||||||||||||||||||||
Atqui, quadrata distantiarum à plano BC, aequalia esse liquet quadratis distantiarumGa naar margenoot+ à plano AD, ac proinde eidem rectangulo ∆PΦ, multiplici per dictum particularum numerum. Ergo spatium applicandum, in sphaera ABC, erit duplum rectanguli ∆PΦ; ideoque aequale ⅖ quadrati à radio EB. Itaque, si sphaera suspensa sit ex puncto in superficie sua A, erit | ES, à centro sphaeraeGa naar margenoot+ E ad centrum agitationis S, aequalis ⅖ semidiametri AE. Totaque AS aequalis 7/10 diametri AD. Si vero ex puncto alio, ut L, sphaera suspensa sit; erit ES aequalis ⅖ tertiae proportionalis duabus LE, EBGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Cylindri.In cylindro, invenimus spatium applicandum aequari 1/12 quadrati altitudinis, una cum ¼ quadrati à semidiametro basis. Unde, si cylindrus à centro basis superioris suspendatur, fit longitudo penduli isochroni aequalis ⅔ altitudinis, una cum semisse ejus, quae sit ad semidiametrum basis ut haec ad altitudinem. | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Conoidis Parabolici.In conoide parabolico, rectangulum oscillationis est 1/18 quadrati altitudinis, cum ⅙ quadrati à semidiametro basis. Unde, si à puncto verticis fuerit suspensum, fit longigitudo penduli isochroni ¾ axis, cum ¼ ejus quae sit ad semidiametrum basis, sicut haec ad axem, id est, una cum ¼ lateris recti parabolae genitricisGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
Centrum oscillationis Conoidis Hyperbolici.In conoide quoque hyperbolico centrum oscillationis inveniri potest. Si enim, exempli gratia, sit conoides [Fig. 114] cujus sectio per axem, hyperbola BAB; axem habens AD, latus transversum AF: erit figura plana ipsi proportionalis BKAKB, contenta basi BB, | & parabolicae lineae portionibus similibus AKB, quae parabolae perGa naar margenoot+ verticem A transeunt, axemque habent GE, dividentem bifariam latus transversum AF, ac parallelum basi BB. Et hujus quidem figurae BKAKB, centrum gravitatis L, tantum distat à vertice A, quantum centrum gravitatis conoidis ABB; estque axis AD ad AL, sicut tripla FA cum dupla AD, ad duplam FA cum sesquialtera AD. Deinde & distantia centri gr. figurae dimidiae ADBK, ab AD, inveniri potest, atque etiam subcentrica cunei super figura BKAKB, abscissi plano per AP, parallelam BB; hujus inquam cunei subcentrica, super ipsa AP, inveniri quoque potest; atque ex his consequenter centrum agitationis conoidis, in quavis suspensione; dummodo axis, circa | |||||||||||||||||||||||||||||||||||
[pagina 334]
| |||||||||||||||||||||||||||||||||||
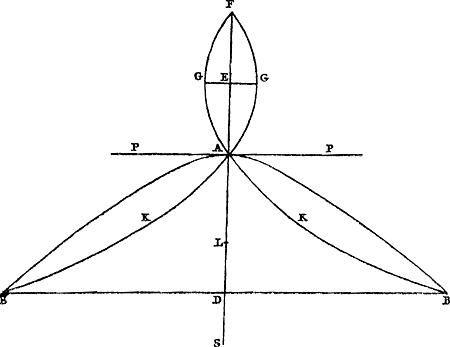
Ga naar margenoot+ [Fig. 114.]
lèle à sa base. Je trouve que si l'on prend l'axe AD égal au latus transversum AF, l'espace qu'il faut diviser par une droite devient égal à 1/20 AD2 + 31/200 DB2; et on a alors AL = 7/10 AD. Par conséquent, lorsque le conoïde considéré est suspendu au sommet A, la longueur AS du pendule isochrone est trouvée égale à 27/35 AD, plus 31/140 de la troisième proportionnelle aux deux grandeurs AD et DBGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Le centre d'oscillation du demi-cône.On pourra enfin trouver le centre d'oscillation aussi dans certaines moitiés de solides divisés par une section par l'axe. Par exemple dans le cas du demi-cône ABC [Fig. 115] ayant son sommet en A et BC pour rayon de la base. Le centre de gravité de ce corps est connu puisque AD = ¾ AE, où AE divise BC en E de telle manière que le rapport ⅔ CB : BE est égal à celui d'un quart de circonférence de cercle à son rayon. En effet, E est alors le centre de gravité du demi-cercle qui constitue la base et sur AE se trouvent donc les centres de gravité de tous les segments parallèles à la base du demi-cône ABD. Or, la figure proportionnelle OVV qu'il faut placer à côté de la figure est la même que celle décrite dans le cas du cône entier: cette figure sert, comme l'on sait, à trouver la somme des carrés des distances des particules du demi-cône au plan horizontal | |||||||||||||||||||||||||||||||||||
[pagina 335]
| |||||||||||||||||||||||||||||||||||
quem movetur, sit basi conoidis parallelus. Atque invenio quidem, si axis AD lateriGa naar margenoot+ transverso AF aequalis ponatur, spatium applicandum aequari 1/20 quadrati AB, cum 31/200 quadrati DB. Tunc autem AL est 7/10 AD. Unde, si conoides hujusmodi ex vertice A suspendatur, invenitur longitudo penduli isochroni, AS, aequalis 27/35 AD, cum 31/140 tertiae proportionalis duabus AD, DBGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||
Centrum oscillationis dimidii Coni.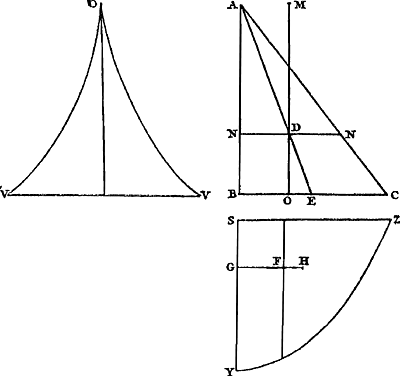 [Fig. 115.]
Denique & in solidis dimidiatis quibusdam, quae fiunt sectione per axem, centrum agitationis invenire licebit. Ut si sit conus dimidiatus ABC [Fig. 115], verticem habens A, diametrum semicirculi ba|seos BC: ejus quidem centrum gravitatis D notumGa naar margenoot+ est, quoniam AD est ¾ rectae AE, ita dividentis BC in E, ut, sicut quadrans circumferentiae circuli ad radium, ita sint ⅔ CB ad BE. Tunc enim E est centrum gravitatis semicirculi baseos, ideoque in AE centra gravitatis omnium segmentorum semiconi ABD, basi parallelorum. Et figura quidem porro proportionalis à latere ponenda, OVV, eadem est quae in cono toto supra descripta fuit: per quam nempe invenietur summa quadratorum, à distantiis particularum semiconi à plano horizontali ND, per centrum gravitatis ducto. | |||||||||||||||||||||||||||||||||||
[pagina 336]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ ND mené par le centre de gravité. Mais pour apprendre à connaître les carrés des distances au plan vertical MDO il faut encore faire usage d'une autre figure proportionnelle SYZ, telle qu'elle est mentionnée dans la Prop. XIV, savoir une figure dont les sections verticales présentent des lignes proportionnelles aux sections correspondantes du demi-cône ABC; et de cette figure il faut connaître la distance à SY du centre de gravité F, distance apparemment égale à celle, DN, du centre de gravité du demi-cône au plan du triangle AB. Si nous appelons HG la subcentrique de l'onglet coupé sur la figure SZY par un plan passant par SY, il faut connaître le rectangle GFH qui, multiplié par le nombre des particules du demi-cône ABC, sera égal aux carrés des distances du demi-cône au plan MDO. Or, il sera possible d'apprendre à connaître de la manière suivante ce rectangle GFH, même lorsqu'on ignore la longueur de la subcentrique HG. Nous avons dit plus haut, en parlant du cône, que les carrés des distances à un plan passant par son axe sont égaux à 3/80 fois le carré du diamètre de sa base ou bien à 3/20 du carré de son rayon multiplié par le nombre des particules du cône entier. Il s'ensuit qu'ici aussi, dans le demi-cône ABC, les carrés des distances au plan AB seront égaux au produit de 3/20 BC2 par le nombre des particules du demi-cône. Mais le rectangle HGF, multiplié par le nombre des particules du demi-cône ABC, est aussi égal aux carrés des distances au plan AB, comme cela résulte de la Prop. IX. Par conséquent le rectangle HGF est égal à 3/20 BC2. Or, si l'on pose AB = a, BC = b et le quart de la circonférence décrite avec le rayon BC = q, on aura EB = 2b2/3q. Et comme ND est égale aux trois quarts de cette dernière longueur, il en résultera que ND ou GF est égale à ½ b2/q. En retranchant le carré de cette expression du rectangle HGF qui était égal à 3/20 BC2, on en conclura que le rectangle GFH est égal à 3/20 b2 - ¼b4/q2. Et ce rectangle, multiplié par le nombre des particules du demi-cône ABC, est égal aux carrés des distances au plan MDO. Mais aux carrés des distances au plan ND est égal, comme dans le cas du cône, le produit de 3/80 AB2 ou 3/80 a2 par le nombre des particules du demi-cône ABC. Par conséquent l'espace total qu'il faut diviser par une droite sera égal ici à 3/80 a2 + 3/20 b2 - ¼b4/q2. Ce résultat permet de trouver le centre d'agitation pour toute suspension du demi-cône, du moins s'il est suspendu à un axe parallèle à la base du triangle AB résultant de la section du cône. On peut encore remarquer que, malgré le fait que la figure SZY est d'une nature absolument inconnue, la subcentrique GH correspondant à un onglet coupé sur elle par un plan passant par SY, est trouvée par les considérations qui précèdent. Car, comme le rectangle HGF s'est montré égal à 3/20 b2 ou 3/20 BC2. et GF = ½ b2/q, il en résulte que GH = 3/10 q. | |||||||||||||||||||||||||||||||||||
[pagina 337]
| |||||||||||||||||||||||||||||||||||
Verum quadrata distantiarum, à plano verticali MDO, ut colligantur, altera quoqueGa naar margenoot+ figura proportionalis SYZ, sicut supra prop. 14. adhibenda est, cujus nempe sectiones verticales, exhibeant lineas proportionales sectionibus sibi respondentibus in semicono ABC. & hujus figurae cognoscenda est distantia centri gr. F ab SY, quam aequalem esse constat distantiae DN, centri gr. semiconi à plano trianguli AB. positâque HG subcentricâ cunei abscissi super figura SZY, ducto plano per SY, noscendum est rectangulum GFH, cujus nempe multiplex, secundum numerum particularum semiconi ABC, aequabitur quadratis distantiarum semiconi in planum MDO. Licebit vero cognoscere rectangulum illud GFH, etiamsi subcentricae HG longitudo ignoretur, hoc modo. Diximus supra, cum de cono ageremus, quadrata distantiarum | à plano per axemGa naar margenoot+ ejus, aequari 3/80 quadrati à diametro basis, sive 3/20 quadrati à semidiametro, multiplicis per numerum particularum coni totius. Unde & hic, in semicono ABC, quadrata distantiarum à plano AB aequalia erunt 3/20 quadrati BC, multiplicis per numerum particularum ipsius semiconi. Sed & rectangulum HGF, muliiplex per numerum particularum semiconi ABC, aequatur quadratis distantiarum à plano AB, ut patet ex propositione 9. Ergo rectangulum HGF aequale 3/20 quadrati BC. Ponendo autem AB ∞ a; BC ∞ b; & quadrantem circumferentiae, radio BC descriptae, ∞ q; sit EB ∞ 2bb/3q. Cujus cum ND tribus quartis aequetur, fiet proinde ND, sive GF ∞ 1bb/2q. Cujus quadratum auferendo à rectangulo HGF, quod erat 3/20 quadrati BC, fiet rectangulum GFH ∞ 3/20 BB - 1b4/4qq. Hoc autem rectangulum, multiplex per numerum particularum semiconi ABC, aequatur quadratis distantiarum à plano MDO. At quadratis distantiarum à plano ND aequantur, ut in cono, 3/80 quadrati AB, sive 3/80 aa, multiplices per numerum particularum semiconi ABC. Itaque, totum spatium applicandum, aequabitur hic 3/80 aa + 3/20 bb - 1b4/4qq. Unde quidem centrum agitationis invenitur in omni suspensione semiconi, dummodo ab axe qui sit parallelus basi trianguli à sectione AB. Notandum vero, cum figura SZY sit ignotae prorsus naturae, subcentricam tamen GH, cunei super ipsa abscissi plano per SY, hinc inveniri. Nam, quia rectangulum HGF aequale erat 3/20 bb, sive quadrati BC, & GF aequalis 1bb/2q, fit inde GH aequalis 3/10 q. | |||||||||||||||||||||||||||||||||||
[pagina 338]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ On pourra trouver en outre les centres d'agitation du demi-cylindre, du demi-conoïde paraboliqueGa naar voetnoot1), et encore d'autres moitiés de solides, ce dont nous laissons la recherche à d'autres.
Ce que nous avons dit du centre d'agitation dans le cas de figures planes obliques, qui s'obtiennent pour ainsi dire par une luxation des figures droites, s'applique aussi au cas des figures solides: les centres d'oscillation des figures obliques ne diffèrent pas de ceux des figures droites. Par exemple, si ABC et AFG [Fig. 110] sont deux cônes, l'un droit, l'autre scalène, ayant le même diamètre et des bases égales, et si l'un et l'autre sont suspendus au sommet ou à des axes quelconques également distants de leurs centres de gravité, ils seront isochrones, pourvu que l'axe d'oscillation du cône scalène soit perpendiculaire au plan du triangle diamétral qui est normal au plan de la baseGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
Proposition XXIII.Régler le mouvement des horloges par l'addition d'un petit poids supplémentaire pouvant être mu vers le haut ou vers le bas sur la verge d'un pendule divisée en certaine manièreGa naar voetnoot3).
Pour arriver à ce résultat, il faut d'abord trouver le centre d'oscillation du pendule lui-même composé de sa verge pondérable et du poids qui y est suspendu à l'extrémité inférieure. Soit AC ou a la longueur de la verge portant le poids [Fig. 116]. Représentonsnous la verge et le poids C qui y est suspendu divisés en particules égales extrêmement petites; que la verge ait b et le poids C c de ces particules, le rapport b: c étant évidemment celui de la gravité de la verge à celle du poids qui y est attaché. La longueur d'un pendule simple isochrone avec le pendule donné s'obtiendra donc en divisant la somme des carrés des distances de toutes les particules au point de suspension A par | |||||||||||||||||||||||||||||||||||
[pagina 339]
| |||||||||||||||||||||||||||||||||||
 [Fig. 110.]
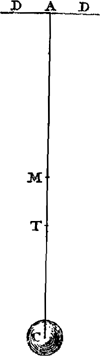 [Fig. 116.]Ga naar margenoot+
Porro, etiam semicylindri, & semiconoidis paraboliciGa naar voetnoot1), centra agitationis inveniri possunt, atque aliorum insuper semisolidorum; quae aliis investiganda relinquimus. Quemadmodum autem in figuris planis, ita & hic in solidis figuris locum habet, quod de obliquarum centris agitationis illic diximus, quae veluti luxatione rectarum constituuntur, quarum centra oscillationis non differunt à centris oscillationis rectarum. Sic, si coni duo fuerunt ABC, AFG [Fig. 110], alter rectus, alter scalenus; quorum & diametri & bases aequales; hi ex vertice suspensi, vel à quibuscunque axibus, aequaliter à centris eorum gravitatis distantibus, isochroni erunt; dummodo axis, unde conus scalenus suspensus est, rectus sit ad planum trianguli per diametrum, quod planum basi est ad angulos rectosGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
Propositio XXIII.Ga naar margenoot+Horologiorum motum temperare, addito pondere exiguo secundario, quod super virga penduli, certa ratione divisa, sursum deorsumque moveri possitGa naar voetnoot3).
Ut hoc expediamus, primo penduli ipsius, ex virga gravitate praedita, & appenso parte ima pondere, compositi, centrum oscillationis inveniendum est. Sit virga, cum appenso pondere, AC, cujus longitudo dicatur a [Fig. 116]. Intelliganrur autem, tum virga ipsa, tum pondus appensum C, in particulas minimas aequales divisa, earumque particularum virga habeat numerum b, pondus vero C numerum c, ponendo nempe b ad c, sicut gravitas virgae ad gravitatem appensi ponderis. Longitudo igitur penduli simplicis, dato isochroni, habebitur, si summa quadratorum à distantiis particularum omnium à puncto suspensionis A, dividatur per summam | |||||||||||||||||||||||||||||||||||
[pagina 340]
| |||||||||||||||||||||||||||||||||||
la somme de ces distancesGa naar margenoot*. Soit AC divisée en deux parties égales au point M et aussi en T de sorte que AT = 2 TC. Puisque M est alors le centre de gravité de la ligne AC et AT la subcentrique de l'onglet coupé sur elle par un plan passant par AD perpendiculaireGa naar margenoot+ à AC, lequel onglet est ici en réalité un triangle, la somme des carrés des distances au point A des particules de la verge sera égale à celle du rectangle AMT et du carré de AM, c.à.d. au rectangle TAM multiplié par le nombre b des particules, c.à.d. ⅓a2b, parce que MA = ½ a et TA = ⅔a et que le rectangle TAM est par conséquent égal à ⅓a2. Mais la somme des carrés au même point A des distances des particules du poids C sera égale à AC2 multiplié par le nombre des particules du poids, c.à.d. à a2c. Par conséquent la somme de tous les carrés, tant ceux des distances des particules de la verge que ceux du poids C, sera ⅓a2b + a2c. Or, la somme des distances des particules de la verge AC au point A est égale à ½ba, c.à.d. au produit de la longueur a de la verge par la moitié du nombre de ses particules. Et la somme des distances de toutes les particules du poids C au même point A est ac. De sorte que la somme des deux groupes de distances est ½ab + ac. En divisant par cette expression la somme des carrés trouvée plus haut, ⅓a2b + a2c, on obtient pour la longueur du pendule isochrone:
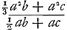 ou ou 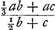 . .
Cette longueur peut donc être construite en faisant que comme la demi-gravité de la verge augmentée de la gravité du poids qui y est attaché est au tiers de la gravité de la verge augmenté de celle du poids, ainsi la longueur AC se rapporte à une autre. Il faut prendre ici la longueur AC depuis le point de suspension A jusqu'au centre de gravité du poids C, puisque nous ne tenons pas compte dans ce calcul de la grandeur du poids: nous le considérons comme occupant un espace extrêmement petit. Supposons maintenant qu'outre le poids C, un deuxième D soit attaché à la verge [Fig. 117] et que la gravité de D ou le nombre de ses particules soit d, tandis que la distance AD = f. Pour trouver le pendule simple isochrone avec notre pendule ainsi composé, il faut ajouter à la somme des carrés considérée plus haut les carrés des distances au point A des particules du poids D, c.à.d. d f f. De sorte que la somme de tous les carrés devient maintenant ⅓a2b + a2c + f2d. Pareillement il faut ajouter à la somme des distances celles des particules du poids D, savoir df. La somme de toutes les distances sera donc ½ba + ca + df. C'est par cette expression qu'il saut diviser la somme des carrés dont il est question plus haut. On obtient ainsi pour la longueur du pendule isochrone 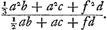
Que si l'on exige que cette longueur du pendule isochrone soit égale à une longueur donnée p, tout le reste étant donné comme auparavant à l'exception de la distance f | |||||||||||||||||||||||||||||||||||
[pagina 341]
| |||||||||||||||||||||||||||||||||||
earundem distantiarumGa naar margenoot*. Secetur AC bifariam in M; tum vero in T, ut AT sit dupla TC. Quia ergo M est centrum gravitatis lineae AC, & AT subcentrica cunei superGa naar margenoot+ ipsa abscissi plano per AD, perpendicularem ad AC; qui cuneus hîc revera triangulum est; erit summa quadratorum, à distantiis particularum virgae à puncto A, | aequalisGa naar margenoot+ rectangulo AMT, una cum quadrato AM; hoc est, rectangulo TAM, multiplici secundum numerum particularum b; hoc est, ⅓aab; quia MA est ½a, & TA ⅔a, ac proinde rectangulum TAM ∞ ⅓aa. Summa vero quadratorum, à distantiis particularum ponderis C ab eodem puncto A, aequabitur quadrato AC, multiplici secundum numerum particularum ipsius ponderis; hoc est, aac. Adeoque summa quadratorum omnium, tam à distantiis particularum virgae, quam ponderis C, erit ⅓aab + aac. Porro, distantiae omnes particularum virgae AC à puncto A, aequantur ½ ba; longitudini scilicet virgae ipsius, quae est a, multiplici secundum semissem numeri particularum quas continet. Et distantiae omnes particularum ponderis C, ab eodem puncto A, sunt ac. Ita ut summa utrarumque distantiarum sit ab + ac. Per quam dividendo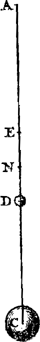 summam quadratorum prius inventam, ⅓aab + aac, fit
summam quadratorum prius inventam, ⅓aab + aac, fit 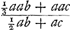 sive sive 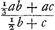 , longitudo penduli isochroni. Quae itaque habebitur, si fiat, ut dimidia gravitas virgae, una cum gravitate appensi ponderis, ad trientem gravitatis virgae, una cum gravitate ejusdem appensi ponderis, ita longitudo AC ad aliam. Oportet autem sumere longitudinem AC, à puncto suspensionis A ad centrum gravitatis ponderis C; cum magnitudinis ejus ratio hic non habeatur, ac veluti minimum consideretur.
Quod si jam, praeter pondus C, alterum insuper D virgae inhaerere intelligatur [Fig. 117], cujus gravitas, seu particularum numerus sit d: distantia vero AD sit f. Ut pendulum siimplex huic ita composito isochronum inveniatur, addenda sunt ad summam superiorem quadratorum, quadrata distantiarum particularum ponderis D à puncto A, quae quadrata apparet esse dff. Adeo ut summa omnium jam sit futura ⅓aab + aac + ffd. Item, ad summam distantiarum, addendae distantiae particularum ponderis D, quae faciunt df. Ac summa proinde distantiarum omnium erit ½ba + + ca + df; per quam dividenda est ista quadratorum summa, & fit , longitudo penduli isochroni. Quae itaque habebitur, si fiat, ut dimidia gravitas virgae, una cum gravitate appensi ponderis, ad trientem gravitatis virgae, una cum gravitate ejusdem appensi ponderis, ita longitudo AC ad aliam. Oportet autem sumere longitudinem AC, à puncto suspensionis A ad centrum gravitatis ponderis C; cum magnitudinis ejus ratio hic non habeatur, ac veluti minimum consideretur.
Quod si jam, praeter pondus C, alterum insuper D virgae inhaerere intelligatur [Fig. 117], cujus gravitas, seu particularum numerus sit d: distantia vero AD sit f. Ut pendulum siimplex huic ita composito isochronum inveniatur, addenda sunt ad summam superiorem quadratorum, quadrata distantiarum particularum ponderis D à puncto A, quae quadrata apparet esse dff. Adeo ut summa omnium jam sit futura ⅓aab + aac + ffd. Item, ad summam distantiarum, addendae distantiae particularum ponderis D, quae faciunt df. Ac summa proinde distantiarum omnium erit ½ba + + ca + df; per quam dividenda est ista quadratorum summa, & fit 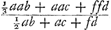 , longitudo penduli isochroni. , longitudo penduli isochroni.
Quod si vero, haec longitudo penduli isochroni, datae aequalis postuletur, quae sit p, & reliqua omnia quae prius data sint, praeter | distantiam AD seu f, quae determinatGa naar margenoot+ | |||||||||||||||||||||||||||||||||||
[pagina 342]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ qui détermine la place du poids D, et qu'il faille trouver cette distance, le calcul sera le suivant: on demande que 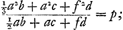
de cette équation résulteront les suivantes: 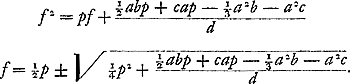 Où il faut remarquer qu'il y a deux racines vraies lorsque ½abp + cap est inférieur à ⅓a2b + a2c, c.à.d. lorsque la longueur p est inférieure à 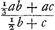 , ce qui est la longueur auparavant trouvée du pendule isochrone, ou la distance du centre d'oscillation au point de suspension, dans le pendule composé de la verge AC et du poids C. , ce qui est la longueur auparavant trouvée du pendule isochrone, ou la distance du centre d'oscillation au point de suspension, dans le pendule composé de la verge AC et du poids C.
D'où il appert que si nous voulons faire en sorte que par l'application du poids D le mouvement du pendule soit accéléré, ce poids peut être placé en deux endroits, tels que D ou E, entre A et C; dans l'un et l'autre cas la même vitesse du pendule en résultera. Ces endroits seront situés à égale distance du point N qui se trouve à la distance ½p du point A, c.à.d. à une distance égale à la moitié du pendule simple avec lequel on exigeait que notre pendule composé serait isochrone. Or, il est clair que lorfque cette longueur p est confidérée comme fort peu inférieure à AC, le point N lui aussi ne sera situé que fort peu au-dessus du point milieu de la verge ACGa naar voetnoot1). De l'équation précédente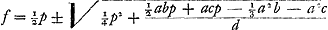 on tire la détermination de la longueur p. En effet, il apparaît que l'expression on tire la détermination de la longueur p. En effet, il apparaît que l'expression 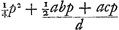 doit ne pas être inférieure à doit ne pas être inférieure à 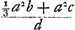 . Par conséquent p ne devra pas être plus petite que . Par conséquent p ne devra pas être plus petite que
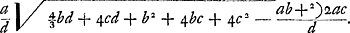 Que si p est égale à cette quantité, c.à.d. si 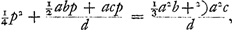 Ga naar voetnoot2) Ga naar voetnoot2)
on aura dans l'équation précédente f = ½p, 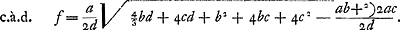 | |||||||||||||||||||||||||||||||||||
[pagina 343]
| |||||||||||||||||||||||||||||||||||
locum ponderis D: sitque invenienda haec distantia, id fiet hoc modo. Nempe, cumGa naar margenoot+ postuletur 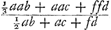 aequale p, orietur ex hac aequatione aequale p, orietur ex hac aequatione
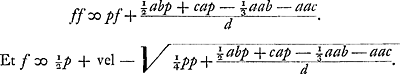 Ubi animadvertendum, duas esse veras radices, si ½abp + cap minus sit quam ⅓aab + aac; hoc est, si longitudo p minor sit quam 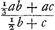 , quae antea inventa fuit longitudo penduli isochroni, sive distantia centri oscillationis à suspensione, in pendulo composito ex virga AC & pondere C. , quae antea inventa fuit longitudo penduli isochroni, sive distantia centri oscillationis à suspensione, in pendulo composito ex virga AC & pondere C.
Unde patet, si velimus efficere, ut, applicato pondere D, acceleretur penduli motus, posse duobus locis, inter A & C, illud disponi, quorum utrolibet eadem celeritas pendulo concilietur: velut in D vel E. Quae loca aequaliter distabunt à puncto N, quod abest ab A, semisse longitudinis p, hoc est, semisse penduli simplicis, cui compositum hoc isochronum postulabatur. Apparet autem, quando haec longitudo p tantum exiguo minor ponitur quam AC, etiam punctum N exiguo superius esse puncto medio virgae ACGa naar voetnoot1). Porro, ex aequatione superiori, 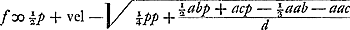 habetur determinatio longitudinis p. Patet enim, 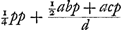 non minus esse debere quam non minus esse debere quam 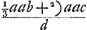 Ga naar voetnoot2). Unde non debebit esse minor quam Ga naar voetnoot2). Unde non debebit esse minor quam
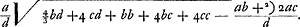 Quod si p aequetur huic quantitati, hoc est, fi 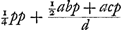 fuerit aequale fuerit aequale 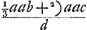 Ga naar voetnoot2), erit jam, in eadem superiori aequatione, Ga naar voetnoot2), erit jam, in eadem superiori aequatione,
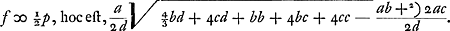 | |||||||||||||||||||||||||||||||||||
[pagina 344]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ Cette formule détermine une distance du poids D au poids A telle que le poids D accélère le mouvement du pendule autant que possible. Pour le réglage des horloges on fait usage comme suit des résultats obtenus. Considérons par exemple un pendule d'horloge qui marque les sécondes par chacune de ses oscillations simples. Que la gravité de la verge soit 1/50 de celle du poids suspendu au bas du pendule; qu'il y ait outre ce poids-là un autre petit poids mobile le long de la verge et dont nous supposons la gravité précisément égale à celle de la verge. On demande où il faut placer ce poids sur la verge pour que le mouvement de l'horloge soit accéléré d'une minute dans un espace de 24 heures. De même où il faut le placer pour obtenir une accélération de deux, de trois, de quatre ou d'un plus grand nombre de minutes. En multipliant le nombre vingt-quatre des heures par soixante, on obtient 1440, nombre des minutes comprises en un jour. Retranchez-en une, lorsqu'il s'agit d'une accélération d'une minute: il en reste 1439. Or, le rapport des carrés de 1440 et de 1439 est à peu près le même que celui des nombres 1440 et 1438. Par conséquent, si la longueur du pendule simple qui marque les secondes est divisée par la pensée en 1440 parties égales et qu'on attribue 1438 de ces parties à un autre pendule, ce dernier avancera par rapport au premier d'une minute en 24 heures. De sorte que p est ici de 1438 parties. Puisque le pendule de l'horloge, composé de la verge métallique et du poids qui y est suspendu, est supposé isochrone avec un pendule simple de 1440 partiesGa naar voetnoot1), il faut d'abord trouver la longueur de cette verge d'après l'équation sus-énoncée. C'est l'expression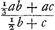 qui à été trouvée egale à la longueur du pendule simple isochrone avec celui composé d'une verge de longueur a et de gravité b et d'un poids y attaché de gravité c. Par conséquent, si la longueur du pendule simple isochrone est appelée s, on aura qui à été trouvée egale à la longueur du pendule simple isochrone avec celui composé d'une verge de longueur a et de gravité b et d'un poids y attaché de gravité c. Par conséquent, si la longueur du pendule simple isochrone est appelée s, on aura 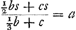 ; et en posant, dans le cas considéré, c = 50, b = 1, f = 1440, on aura pour la longueur de la verge a = 1444 ⅘.
Ensuite, puisque nous avions ; et en posant, dans le cas considéré, c = 50, b = 1, f = 1440, on aura pour la longueur de la verge a = 1444 ⅘.
Ensuite, puisque nous avions
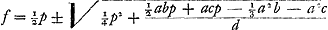 , on aura , on aura
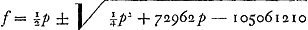 ; et, p étant de 1438 parties comme nous l'avons dit, on trouvera f = 1331½. Il est question de parties telles que s, longueur du pendule simple qui marque les secondes par ses oscillations, en contient 1440. Si nous désignons cette dernière longueur per trois pieds horaires, comme nous l'avons déjà fait, f aura 33 pouces et 3 douzièmes de pouce, qu'on appelle lignes. En d'autres termes, pour connaître le lieu du poids D qui donne une accélération d'une minute en 24 heures, il faut retrancher cette dernière longueur f de ; et, p étant de 1438 parties comme nous l'avons dit, on trouvera f = 1331½. Il est question de parties telles que s, longueur du pendule simple qui marque les secondes par ses oscillations, en contient 1440. Si nous désignons cette dernière longueur per trois pieds horaires, comme nous l'avons déjà fait, f aura 33 pouces et 3 douzièmes de pouce, qu'on appelle lignes. En d'autres termes, pour connaître le lieu du poids D qui donne une accélération d'une minute en 24 heures, il faut retrancher cette dernière longueur f de
| |||||||||||||||||||||||||||||||||||
[pagina 345]
| |||||||||||||||||||||||||||||||||||
Quo determinatur distantia ponderis D à puncto A, ex qua maxime omnium acceleretGa naar margenoot+ motum penduli. Atque haec ad horologiorum usum sic porro adhibentur. Sit, exempli gratia, pendulum horologii, quod singulis oscillationibus scrupula secunda notet. Virgae autem gravitas sit 1/30 gravitatis appensi ponderis in imo pendulo: &, praeter hoc, sit aliud exiguum pondus mobile secundum virgae longitudinem, cujus gravitas ea|dem ponaturGa naar margenoot+ quae ipsius virgae. Quaeritur jam, quo loco hoc virgae imponendum, ut uno scrupulo primo acceleretur horologii motus, spatio 24 horarum. Item, ubi collocandum, ut duorum scrupulorum primorum sit acceleratio; item, ut trium, quatuor, atque ita porro. Ductis viginti quatuor horis sexagies, fiunt 1440, quot nempe scrupula prima una die continentur. Ex his unum aufer, quando unius scrupuli acceleratio quaeritur: supersunt 1439. Ratio autem 1440 ad 1439 duplicata, proxime est ea quae 1440 ad 1438. Ergo, si penduli simplicis, secunda scrupula notantis, longitudo divisa intelligatur in partes aequales 1440, earumque 1438 alii pendulo tribuantur, hoc praecedet alterum illud, in 24 horis, uno scrupulo primo. Adeo ut hic p valeat partes 1438. Quia autem pendulum horologii, ex virga metallica & pondere appenso compositum, isochronum ponitur pendulo simplici partium 1440Ga naar voetnoot1); invenienda primum est virgae illius longitudo, ex aequatione superius posita. Erat nempe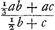 aequale longitudini penduli simplicis, quod isochronum composito ex virga habente longitudinem a, gravitatem b, & pondere affixo cujus gravitas c. Ergo si longitudo penduli simplicis isochroni dicatur s. Erit aequale longitudini penduli simplicis, quod isochronum composito ex virga habente longitudinem a, gravitatem b, & pondere affixo cujus gravitas c. Ergo si longitudo penduli simplicis isochroni dicatur s. Erit 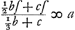 , positoque, ut hic, c ∞ 50; b ∞ 1; s ∞ 1440; fiet, a ∞ 1444 ⅘, longitudo virgae.
Jam, quia erat , positoque, ut hic, c ∞ 50; b ∞ 1; s ∞ 1440; fiet, a ∞ 1444 ⅘, longitudo virgae.
Jam, quia erat
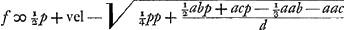 , fiet , fiet
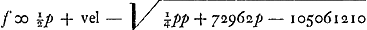 . Unde porro, si p sit, uti diximus, partium 1438; invenietur f ∞ 1331 ½, qualium nempe s, seu pendulum simplex, secunda scrupula oscillationibus designans, continet 1440. Cujus longitudo si pedum trium statuatur, quos horarios vocavimus, habebit f uncias 33, & 3 unciarum uncias, quas lineas vocant. Vel, auferendo hanc longitudinem f à tota trium pedum longitudine, supererunt unciae duae, lineae 9, à centro oscillationis penduli compositi sursum sumendae, ut habeatur locus ponderis D, unius scrupuli primi acce- . Unde porro, si p sit, uti diximus, partium 1438; invenietur f ∞ 1331 ½, qualium nempe s, seu pendulum simplex, secunda scrupula oscillationibus designans, continet 1440. Cujus longitudo si pedum trium statuatur, quos horarios vocavimus, habebit f uncias 33, & 3 unciarum uncias, quas lineas vocant. Vel, auferendo hanc longitudinem f à tota trium pedum longitudine, supererunt unciae duae, lineae 9, à centro oscillationis penduli compositi sursum sumendae, ut habeatur locus ponderis D, unius scrupuli primi acce-
| |||||||||||||||||||||||||||||||||||
[pagina 346]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ la longueur totale de trois pieds: il reste alors 2 pouces et 9 lignes qu'il faut prendre vers le haut à partir du centre d'oscillation du pendule composé. Nous avons examiné de la même manière les autres distances qu'il faut marquer sur la verge, en attribuant diverses valeurs à la longueur p, et nous les indiquons dans la table suivante. C'est fuivant les nombres de cette table qu'a été divisée la verge du pendule représentée plus haut dans la Description de l'Horloge. Les accélérations par jour, comme nous l'avons déjà dit en cet endroit, augmentent chaque fois de 15 secondes, ou d'un quart de minute. Par exemple si l'on trouve que l'horloge, lorsque le poids mobile est fixé à la marque 73,4, retarde en 24 heures de 15 secondes, il faudra pousser le poids D vers le haut jusqu'au nombre 85,6 pour corriger ce retard.
Le centre d'oscillation est situé au-dessus du centre de gravité C de 1,4 parties. | |||||||||||||||||||||||||||||||||||
Proposition XXIV.Qu'il est impossible de tenir compte du centre d'oscillation dans le cas de pendules suspendus entre des cycloïdesGa naar voetnoot1); et comment on surmonte la difficulté qui en résulte.
Si quelqu'un compare par un examen subtil ce que nous avons démontré plus haut à propos du pendule suspendu entre des cycloïdes avec nos considérations sur le centre d'oscillation, il lui semblera qu'il manque quelque chose à la parfaite égalité des oscillations dont nous nous louons. Et premièrement il doutera fi, pour trouver le cercle générateur de la cycloïde, il faut prendre la longueur du pendule depuis le point de | |||||||||||||||||||||||||||||||||||
[pagina 347]
| |||||||||||||||||||||||||||||||||||
lerationem praestans tempore 24 horarum. Eodem modo reliquas distantias, quibusGa naar margenoot+ virga dividenda est, calculo investigavimus, aliam atque aliam ponendo longitudinem p: ejasque subjecta tabella exhibe|mus, secundum cujus numeros etiam virga penduliGa naar margenoot+ divisa est, quae superius in descriptione horologii fuit exhibita. Procedunt autem accelerationes diurnae, ut jam illic advertimus, per 15 scrupula secunda, seu primorum scrupulorum quadrantes. Ex. gr. si, pondere mobili D haerente in parte 73,4, inveniatur horologium tardius justo incedere, in 24 horis, differentiâ 15 secundorum scrupulorum; oportebit sursum adducere pondus D, usque ad numerum 85,6 ut corrigatur.
Centrum oscillationis altius est centro gravitatis C partibus 1,4. | |||||||||||||||||||||||||||||||||||
Propositio XXIV.Centri oscillationis rationem haberi non posse, in pendulis inter Cycloides suspensisGa naar voetnoot1); & quomodo hinc orta difficultas tollatur.
Si quis, subtili examine, contulerit ea quae in superioribus, de pendulo inter cycloides suspenso, demonstravimus, cum his quae ad centrum oscillationis pertinent; videbitur ei deesse aliquid ad perfectam illam, quam praeferimus, oscillationum aequalitatem. Ac primo dubitabit, an, ad inveniendum circulum cycloidis genitorem, penduli longitudo accipienda sit à puncto suspensionis ad | centrum gravitatis appensi plumbi,Ga naar margenoot+ | |||||||||||||||||||||||||||||||||||
[pagina 348]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ suspension jusqu'au centre de gravité du poids qui y est attaché, ou bien jusqu'au centre d'oscillation qui dissère souvent de l'autre d'un intervalle sensible et d'autant plus grand que la sphère ou la lentille de plomb est plus volumineuse. Comment en sera-t-il par exemple lorsque le diamètre de la sphère est égal au quart ou au tiers de la longueur du pendule? Et si nous disons que cette longueur doit être comptée jusqu'au centre d'oscillation, il ne sera pourtant pas clair comment ce que nous avons démontré au sujet du centre d'oscillation s'applique à un pendule qui change continuellement de longueur, comme le fait celui qui se meut entre des cycloïdes. Car il pourrait sembler que le centre d'oscillation change aussi de place lorsque la longueur prend une valeur après une autre, ce qu'il ne faut pourtant pas entendre de cette façon. La chose est certes fort difficile à expliquer si nous recherchons une exactitude parfaite; en effet, dans la démonstration de l'égalité des temps dans la cycloïde nous avons considéré le mobile qui se mouvait suivant elle comme si c'était un point pesant. Mais si nous nous en tenons à la pratique, cette difficulté ne doit pas être considérée comme sort importante, puisque dans les horloges il ne faut pas que le poids qui constitue le corps oscillant soit si grand (toutefois, plus ce poids est grand, mieux cela vaut) que la différence des centres de gravité et d'oscillation puisse causer des troubles. Si cependant nous désirons absolument éviter cette difficulté, nous y arriverons en rendant la sphère ou lentille du pendule mobile autour de son axe horizontal: il faudra insérer les extrémités de ces axes de part et d'autre au bas de la verge du pendule, laquelle doit donc à cet effet être fendue en deux de ce côté. En effet, de cette manière il arrive, d'après la nature du mouvement, que la sphère du pendule garde perpétuellement la même position par rapport à un plan horizontal et qu'ainsi tous ses points parcourent les mêmes cycloïdes, tout aussi bien que le centre. Par conséquent la considération des centres d'oscillation ne s'applique plus à ce mouvement, et un pendule de ce genre présente un isochronisme aussi parfait que si toute sa gravité était réunie en un seul point. | |||||||||||||||||||||||||||||||||||
Proposition XXV.De la manière d'établir une mesure universelle et perpétuelleGa naar voetnoot1).
Une mesure certaine et permanente des grandeurs que ne soit sujette à aucunes rencontres et ne puisse être abolie ou corrumpue par l'injure ou la longueur des temps, est une chose sort utile et recherchée depuis longtemps par beaucoup de gens. Si l'on en avait trouvé une aux temps anciens, les disputes actuelles sur la mesure du pied antique romain, grec ou hébraïque ne seraient pas pleines de tant de perplexités. Or, cette mesure est aisément établie au moyen de notre horloge, tandis que sans celle-ci elle ne peut pas ou fort difficilement être obtenue. Il est vrai que ceci a été tenté par quelques personnes par la simple oscillation de pendules, savoir en comptant le nombre d'oscillations correspondant à une révolution entière du ciel, ou à celle d'une partie du ciel connue par les distances de certaines étoiles fixes entre elles suivant leur | |||||||||||||||||||||||||||||||||||
[pagina 349]
| |||||||||||||||||||||||||||||||||||
an vero ad centrum oscillationis; quod, ab altero illo, saepe sensibili intervallo distatGa naar margenoot+ atque eo majore, quo major fuerit sphaera aut lens plumbea. Quid enim, si sphaerae diameter quartam, aut tertiam partem, penduli longitudinis aequet? Quod si ad centrum oscillationis illam longitudinem accipiendam dicamus, non tamen expediet quo pacto ea, quae de centro oscillationis ostensa sunt, conveniant pendulo continue longitudinem suam immutanti, quale illud quod inter cycloides movetur. Posset enim videri, etiam centrum oscillationis mutari, ad singulas diversas longitudines; quoc tamen hoc modo intelligendum non est. Res sane explicatu difficillima, si omnimodam ἀϰρἰβειαν sectemur. Nam in demonstratione temporum aequalium in cycloide, mobile, per eam delatum, veluti punctum gravitate praeditum consideravimus. Sed, si ad effectum spectemus, non magni facienda est difficultas haec; cum ponderis, quo pendulum constat, magnitudo in horologiis tanta non requiratur (etsi quo majus eo melius) ut differentia centrorum gravitatis, & oscillationis, aliquid hic turbare possit. Quod si tamen effugere prorsus has tricas velimus, id ita consequemur, si sphaeram lentemve penduli, circa axem suum horizontalem, mobilem efficiamus: axis extrema utrinque, virgae penduli imae, inferendo: quae idcirco ut bifida hac parte sit necesse est. Fit enim hoc modo, ex motus natura, ut eandem perpetuo positionem, respectu horizontalis plani, sphaera penduli servet, atque ita puncta ejus quaevis, aeque ac centrum ipsum, cycloides easdem percurrant. Unde cessat hic jam centrorum oscillationis consideratio; nec minus perfectam temporum aequalitatem tale pendulum consequitur, quam si puncto unico omnis ejus gravitas contineretur. | |||||||||||||||||||||||||||||||||||
Propositio XXV.De mensurae universalis, & perpetuae, constituendae rationeGa naar voetnoot1).
Certa, ac permanens magnitudinum mensura, quae nullis casibus obnoxia sit, nec temporum injuriis, aut longinquitate aboleri aut corrumpi possit, res est & utilissima, & à multis pridem quaesita. Quae si priscis temporibus reperta fuisset, non tam perplexae nunc forent, de pedis Romani, Hebraeique veteris modulo, disceptationes. Haec vero mensura, Horologii nostri opera, facile constituitur; cum sine illo nequaquam, aut aegre admodum, ha|beri possit. Etsi enim, simplici pendulorum oscillatione,Ga naar margenoot+ hoc à quibusdam tentatum fuerit, numerando recursus qui tota caeli conversione continentur, vel parte ejus cognita, per fixarum stellarum distantias, secundum ascensio- | |||||||||||||||||||||||||||||||||||
[pagina 350]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ ascension droite; mais d'une part on n'arrive pas de cette manière à une certitude égale à celle qu'on atteint par l'emploi des horloges, et d'autre part ce labeur est extrêmement pénible et ennuyeux à cause de l'exactitude avec laquelle il faut compter les oscillationsGa naar voetnoot1). Or, parce qu'il n'y faut pas seulement les horloges, mais que la théorie des centres d'oscillation contribue aussi quelque chose à la recherche fort exacte de cette mesure, nous ne traitons de ce sujet qu'ici à la fin, après avoir établi cette théorie. Les horloges les plus propres à cela sont celles dont les oscillations marquent les secondes ou demi-secondes et qui sont aussi pourvues d'indices ou d'aiguilles pour les indiquer. En esset, après qu'une horloge de ce genre a été réglée par l'observation d'étoiles fixes sur la durée moyenne des jours, suivant la méthode que nous avons enseignée dans la Description de l'Horloge, il faut suspendre à côté d'elle un autre pendule simple, c'à.d. une sphère de plomb ou d'une autre matière pesante attachée à un fil mince, et mettre ce pendule en mouvement par une légère impulsion; il faut ensuite allonger ou raccourcir le fil jusqu'à ce que ses oscillations s'accordent parfaitement durant un quart d'heure ou une demi-heure avec celles du pendule qui fait partie de l'horloge. J'ai dit qu'il faut mettre le pendule en mouvement par une légère impulsion, parce que de petites oscillations, p.e. de 5 ou 6 degrés, ont des périodes passablement égales, mais qu'il n'en est plus ainsi des grandes. Si l'on prend alors la mesure de la distance du point de suspension au centre d'oscillation du pendule simple et qu'on divise cette distance, dans le cas où les oscillations simples correspondent à des secondes, en trois parties égales, chacune de celles-ci donnera la longueur du pied que nous avons appelé ci-dessus Pied HoraireGa naar voetnoot2), et qui peut de sorte non seulement être déterminé par toutes les nations, mais aussi être reconstitué dans les siècles à venir. D'où il suit que les longueurs de tous les autres pieds étant une fois exprimées par leurs rapports à ce pied-ci, elles pourront désormais être connues elles aussi avec certitude. Nous avons déjà dit plus haut que le pied parisien est au pied horaire tel que nous l'avons défini ici comme 864 est à 881, ce qui revient à dire que, le pied parisien étant donné, le pendule simple dont les oscillations correspondent aux secondes a une longueur de trois de ces pieds augmentés de huit lignes et demie. Et le pied parisien est au pied rhénan dont on se sert dans notre patrie comme 144 est à 139, c.à.d. le premier surpasse le second de 5 lignes parisiennes. Le pied rhénan lui aussi, et d'autres pieds quelconques, acquièrent ainsi une longueur fixée pour toujours. Nous avons fait voir plus haut comment le centre d'oscillation est trouvé pour une sphère suspendue à un fil de longueur quelconque; savoir que si, comme la distance du point de suspension au centre de la sphère est à son rayon, ainsi ce dernier est à une autre longueur, les deux cinquièmes de cette longueur-là portées vers le bas à partir du centre aboutissent au centre d'oscillation cherché. Or, il apparaît facilement pourquoi la considération de ce centre est nécessaire à la détermination exacte du pied horaire. Car si la distance est prise depuis le point de suspension jusqu'au centre de la sphère, mais qu'on ne définit pas la grandeur de la sphère par rapport à la longueur | |||||||||||||||||||||||||||||||||||
[pagina 351]
| |||||||||||||||||||||||||||||||||||
nem rectam; nec certitudo eadem hoc modo, quae adhibitis horologiis, contingit, &Ga naar margenoot+ labor longe est molestissimus ac taediosissimus, propter numerandi solicitudinemGa naar voetnoot1). Quia autem, praeter horologia, aliquid, ad exactissimam hujus mensurae inquisitionem, etiam centrorum oscillationis notitia confert; ideo hic demum, post eorum tractationem, hanc determinationem subjicimus. Aptissima huic rei sunt horologia, quorum oscillationes singulae secunda scrupula, vel eorum semisses, notant, quaeque indicibus etiam, ad ea demonstranda, instructa sunt. Postquam enim, ad mediocrem dierum longitudinem, ejusmodi horologium, fixarum stellarum observationibus, compositum fuerit, methodo illa quam in horologii descriptione ostendimus: aliud pendulum simplex, hoc est, sphaera plumbea, aut alia materia gravi constans, ex tenui filo religata, juxta suspendenda est, motuque exiguo impellenda; ac tantisper producenda, aut contrahenda fili longitudo, donec recursus ejus, per quadrantem horae, aut semissem, una ferantur cum reciprocationibus penduli horologio aptati. Dixi autem exiguo motu impellendum pendulum, quia oscillationes exiguae, puta 5 vel 6 partium, satis aequalia tempora habent, magnae vero non item. Tunc, acceptâ mensurâ distantiae, à puncto suspensionis ad centrum oscillationis penduli simplicis; eâque, si recursus singuli scrupula secunda valeant, in tres partes divisâ; facient hae singulae longitudinem pedis, quem Horarium in superioribus vocavimusGa naar voetnoot2): quique, hoc pacto, non solum ubique gentium constitui possit, sed & venturo aevo redintegrari. Adeo ut & moduli pedum omnium aliorum, semel ad hunc proportionibus suis expressi, certò quoque in posterum cognosci possint. Sicut jam supra, pedem Parisiensem ad hunc horarium esse diximus, ut 864 ad 881; quod idem est ac si, posito prius pede Parisiensi, dicamus tribus hujusmodi pedibus, cum octo lineis & dimidia, constitui pendulum simplex, cujus oscillationes scrupulis secundis horariis responsurae sint. Pes autem Parisiensis ad Rhenanum, quo in Patria nostra utuntur, se habet ut 144 ad 139; hoc est, quinque lineis suis diminutus, alteram illum relinquit. Atque ita & hic pes, & alii quilibet, perpetuo duraturas mensuras accipiunt. Quomodo autem centrum oscillationis in sphaera, ex qualibet | longitudine suspensa,Ga naar margenoot+ inveniatur, in superioribus demonstratum est. Nempe, si fiat ut distantia inter punctum suspensionis & sphaerae centrum, ad semidiametrum ejus, ita haec ad aliam; ejus duas quintas, à centro deorsum acceptas, terminari in quaesito oscillationis centro. Facile autem apparet cur necessaria sit hujus centri consideratio, ad accuratam pedis Horarii constitutionem. Nam, si à puncto suspensionis ad sphaerae centrum distantia accipiatur, sphaerae autem magnitudo non definiatur proportione ad fili longitudinem, non erit | |||||||||||||||||||||||||||||||||||
[pagina 352]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ du fil, la mesure du pendule dont les oscillations correspondent aux secondes ne sera pas absolument certaine: plus la sphère est grande, plus la distance du centre de la sphère au point de suspension sera trouvée petite. En effet, dans les pendules isochrones les distances des centres d'oscillation aux points de suspension sont toujours les mêmes, mais dans le cas d'une plus grande sphère le centre d'oscillation descend plus bas audessous du centre que dans celui d'une sphère plus petite. C'est pourquoi ceux qui avant cette détermination du centre d'oscillation ont entrepris de nous donner une méthode pour trouver la mesure universelle - ce que la noble Société Royale anglaise s'est proposé depuis le moment où fut inventée notre horlogeGa naar voetnoot1), et après elle le très savant astronome de Lyon, Gabriel MoutonGa naar voetnoot2) - ceux-ci, dis-je, ont été obligés de définir le diamètre du globule suspendu soit par rapport à la longueur du fil, disant qu'il en aurait par exemple la trentième partie, soit d'après une mesure connue, tel que le doigt ou le pouce. Mais de cette dernière façon on prend déjà comme connu ce qu'il fallait chercher; je n'ignore pas cependant que l'erreur sera à peine sensible pourvu que les dimensions des sphères ne surpassent pas beaucoup celle dont j'ai parlé. De la première façon la chose réussirait assez bien, mais dans ce cas il faudrait prendre la peine de compter les oscillations et se servir du calcul. Il est donc préférable de faire usage des centres d'oscillation et de suivre ainsi une voie certaine en ne tenant compte que des lois qui s'y appliquent. En agissant ainsi il vaut mieux employer de grandes que de petites sphères parce que les premières sont moins influencées par la résistance de l'air. D'ailleurs ce ne sont pas seulement les sphères suspendues à un fil, mais aussi les cônes, les cylindres et tous les autres corps, y compris les plans, dont nous avons fait connaître plus haut les centres d'oscillation, qui sont propres à la recherche de cette mesure, puisque pour tous les pendules isochrones il y a un intervalle déterminé et égal entre le point de suspension et le centre d'oscillation. Et nous ne sommes pas obligés de nous servir des horloges qui indiquent par les oscillations simples de leurs pendules les secondes ou demi-secondes: nous pouvons encore atteindre notre but à l'aide d'horloges munies de pendules d'autres longueurs quelconques, pourvu qu'on connaisse par les proportions des roues, en d'autres termes par les nombres de leurs dents, le nombre des oscillations qui sont exécutées en un certain temps. En effet, le pendule simple ayant été trouvé dont les oscillations correspondent chacune à une, deux ou trois oscillations du pendule de l'horloge, on en conclura le nombre des oscillations que le pendule simple exécute en une heure. Et en portant ce nombre au carré, on aura ceci: le carré de 3600, nombre des secondes qui font l'heure, sera au carré prénommé comme la longueur du pendule simple trouvé (longueur qu'il faut toujours compter depuis le point de suspension jusqu'au centre d'oscillation) est à la longueur du pendule horaire de trois pieds dont nous avons parlé. Ceci résulte en effet du fait que les longueurs de deux pendules quelconques sont entre elles comme les carrés des temps dans lesquels se font leurs oscillations; par conséquent ces longueurs sont inversement proportionnelles aux carrés des nombres des oscillations | |||||||||||||||||||||||||||||||||||
[pagina 353]
| |||||||||||||||||||||||||||||||||||
certa mensura penduli cujus recursus secunda scrupula metiantur; sed quo major eritGa naar margenoot+ ejus sphaera, hoc minor invenietur mensura illa, inter centrum sphaerae & punctum suspensionis intercepta. Quia in isochronis pendulis, centra quidem oscillationis à punctis suspensionum aequaliter distant; amplius autem descendit centrum oscillationis infra centrum sphaerae majoris, quam minoris. Hinc necesse suit illis, qui, ante hanc centri oscillatorii determinationem, mensura? universalis constituendae rationem inierunt; quod, jam inde à prima Horologii nostriinventione, nobilisilla Societas Regia Anglicana sibi negotium sumpsitGa naar voetnoot1), & recentius doctissimus Astronomus Lugdunensis, Gabriel MoutonusGa naar voetnoot2); his, inquam, necesse fuit designare globuli suspensi diametrum, vel proportione certa ad fili longitudinem, cujus nempe tricesimam vel aliam partem aequaret; vel mensura quadam cognita, ut digiti vel pollicis. Sed hoc posteriore modo, ponitur jam certi aliquid, quod id ipsum est quod quaerendum est: etsi scio vix sensibilem errorem fore, dummodo sphaerae istam, quam jam dixi, magnitudinem non multum excedant. Priore autem posset quidem aliquo pacto res explicari; sed ita, ut numerandarum oscillationum labor subeundus sit, calculoque etiam utendum. Quamobrem praestat, centra oscillationis adhibendo, certam rationem sequi, nullisque praeter necessitatem legibus obligari. atque hic jam majoribus sphaeris quam exiguis potius utendum, quod illae occursu aëris minus impedianrur. Caeterum, non sphaerae tantum ex filo suspensae, sed & coni, cylindri, aliaque omnia solida, planaque, quorum centra oscillationis superius exhibuimus, ad hanc mensuram investigandam, apta sunt; quoniam, à puncto suspensionis ad centrum oscillationis, certum idemque omnibus isochronis pendulis est intervallum. Neque etiam illa duntaxat horologia, quae secunda scrupula aut eorum semisses singulis penduli recursibus indicant, ad haec usur|pare possumus; sed & aliâ quâcunque penduli longitudine instructisGa naar margenoot+ propositum obtinebitur, dummodo ex rotarum proportionibus, seu dentium numero, cognoscatur numerus oscillationum certo tempore peragendarum. Invento enim pendulo simplici, cujus librationes singulae conveniant vel singulis, vel binis ternisve recursibus horologii, constabit jam hinc, quot penduli illius vices horae spatio transigantur. Quarum numerus si quadretur, erit ut quadratum è 3600, numero scrupulorum secundorum horam unam efficientium, ad quadratum illius numeri, ita longitudo penduli simplicis inventi, (quae longitudo semper à puncto suspensionis ad centrum oscillationis accipienda est) ad longitudinem penduli illius horarii tripedalis, quod diximus. Hoc enim inde constat, quod duorum quorumvis pendulorum longitudines sunt inter se, sicut quadrata temporum quibus singulae oscillationes transeunt; ideoque contrariam rationem habent quadratorum à numeris, quos efficiunt oscillatio- | |||||||||||||||||||||||||||||||||||
[pagina 354]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ exécutées en des temps égaux. Observons que tandis que jusqu'ici ce théorème sur les longueurs des pendules, savoir le théorème de la proportionnalité des longueurs aux carrés des périodes, n'avait été prouvé que par l'expérience, sa démonstration est maintenant manifeste d'après ce que nous avons exposé plus haut. En effet, comme nous avons prouvé que le temps d'une oscillation d'un pendule suspendu entre des cycloïdes a un rapport déterminé à celui d'une chute verticale d'une hauteur égale à la moitié de la longueur du pendule, savoir celui de la circonférence du cercle à son diamètre, on en conclut aisément que les périodes de deux pendules sont entre elles comme les temps des chutes verticales de hauteurs égales à leurs demi-longueurs. Mais comme ces demi-hauteurs, ou les hauteurs entières, ont entre elles un rapport égal à celui des carrés des temps dans lesquels elles sont parcourues dans une chute verticaleGa naar margenoot*, elles auront aussi entre elles un rapport égal à celui des carrés des périodes. Or, les oscillations extrêmement petites d'un pendule simple ne diffèrent pas sensiblement de celles d'un pendule suspendu entre des cycloïdes, les longueurs étant les mêmes. Par conséquent les longueurs des pendules simples seront aussi entre elles comme les carrés des périodes d'oscillations fort petitesGa naar voetnoot1). Que si quelqu'un ne fuit pas le travail de mesurer les oscillations qui sont exécutées en une heure ou en une demi-heure, et qu'il a à sa disposition une horloge dont un indice ou une aiguille fait voir les secondes, il connaîtra de cette manière le nombre d'oscillations correspondant à une heure quelle que soit la longueur du pendule simple considéré; et de là il tirera par le calcul, comme auparavant, la longueur du pendule de trois pieds qui correspond aux secondes. | |||||||||||||||||||||||||||||||||||
Proposition XXVIGa naar voetnoot2).Déterminer l'espace que les corps graves parcourent en tombant durant un certain temps.
Tous ceux qui ont cherché jusqu'ici à mesurer cet espace ont jugé nécessaire d'en venir aux expériences, par lesquelles, de la manière qu'elles ont été instituées jusqu'à ce jour, on n'arrive pas aisément, à cause de la grande vitesse finale des corps tombants, à une détermination exacte. Mais d'après notre Prop. XXV de la Descente des Corps graves, nous pouvons, lorsque la longueur du pendule correspondant aux secondes est connue atteindre le but proposé sans expérience par une conséquence certaine. Nous rechercherons premièrement l'espace qu'un corps grave parcourt en une seconde, duquel on pourra ensuite tirer tous les autres. Comme la longueur du pendule à secondes est, comme nous l'avons dit, de trois pieds horaires et que le temps d'une fort petite oscillation est au temps d'une chute verticale d'une hauteur égale à la moitié du pendule comme la circonférence du cercle est à son diamètre, c.à.d. comme 355 est à 113; si l'on fait que comme le premier de ces nombres est au second, ainsi le temps d'une seconde ou de soixante tierces est à un autre temps, ce dernier sera de 19 1/10‴: c'est là le temps d'une chute de la hauteur du demi-pendule | |||||||||||||||||||||||||||||||||||
[pagina 355]
| |||||||||||||||||||||||||||||||||||
nes aequalibus temporum intervallis peractae. Nam, cum hactenus experientiâ tantumGa naar margenoot+ comprobatum fuerit Theorema illud, de pendulorum longitudinibus; eas nempe duplicatam habere rationem temporum, quibus oscillationes singulae peraguntur; nunc ejus demonstratio ex superius traditis manifesta est. Cum enim ostenderimus, singulos recursus penduli, inter cycloides suspensi, ad casum perpendicularem, è dimidia penduli longitudine, certam rationem habere; eam scilicet quam circumferentia circuli ad diametrum suam; facile hinc colligitur, tempora oscillationum in duobus pendulis esse inter se, sicut tempora descensus perpendicularis ex dimidiis eorum altitudinibus. Quae altitudines dimidiae, sive etiam totae, cum habeant rationem duplicatam temporum, quibus ipsae descensu perpendiculari percurrunturGa naar margenoot*; eaedem quoque duplicatam rationem habebunt temporum, quae oscillationes singulas metiuntur. Ab oscillationibus autem minimis penduli, inter cycloides suspensi, non differunt sensibiliter oscillationes minimae penduli simplicis, cujus eadem sit longitudo. Itaque & pendulorum simplicium longitudines, duplicatam rationem habebunt temporum, quibus oscillationes minimae transigunturGa naar voetnoot1). Quod si quis oscillationum numerandarum, quae horae aut semihorae tempore transeunt, laborem non defugiat; horologiumque adsit, cujus index secunda scrupula demonstret; quaecunque accipiatur penduli simplicis longitudo, ejus numerus oscillationum, quae hora una continentur, hoc modo cognoscetur; atque inde longitudo penduli tripedalis, ad secunda scrupula, ut antea, calculo prodibit. | |||||||||||||||||||||||||||||||||||
Propositio XXVIGa naar voetnoot2).Ga naar margenoot+Spatium definire, quod gravia, perpendicularitercadentia, dato tempore percurrunt.
Hanc mensuram quicunque hactenus investigarunt, experimenta consulere necesse habuerunt; quibus, prout hactenus instituta fuere, non facile ad exactam determinationem pervenitur, propter velocitatem cadentium, sub finem motus acquisitam. Ex nostra autem prop. 25, de Descensu gravium, cognitaque longitudine penduli ad secunda scrupula, absque experimento, per certam consequentiam, rem expedire possumus. Ac primo quidem spatium illud inquiremus, quod unius scrupuli secundi tempore grave praeterlabitur; ex quo quaelibet alia deinde colligere licebit. Quia igitur penduli, ad secunda scrupula, longitudinem diximus esse pedum Horariorum 3: tempus autem unius oscillationis minimae, est ad tempus descensus perpendicularis ex dimidia penduli altitudine, ut circumferentia circuli ad diametrum, hoc est, ut 355 ad 113: si fiat, ut numerus horum prior ad alterum, ita tempus unius secundi surupuli, sive sexaginta tertiorum, ad aliud; fient 19‴ 1/10, tempus descensus per dimidiam penduli altitudinem, | |||||||||||||||||||||||||||||||||||
[pagina 356]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ laquelle est de 18 pouces du pied. Mais comme les carrés des temps sont entre eux, ainsi le sont aussi les espaces parcourus en ces temps, comme cela a été démontré dans la proposition précédente. Prenons donc une longueur telle que le carré de 19 1/10‴ soit au carré de 60‴, c.à.d. que 36481 soit à 360000, comme 18 pouces sont à elle: on trouvera ainsi la longueur de 14 pieds, 9 pouces, 6 lignes pour l'espace parcouru en tombant en une seconde. Mais attendu que le pied horaire est au pied parisien comme 881 est à 864, la même hauteur, réduite à cette mesure, sera à peu près de 15 pieds et un pouceGa naar voetnoot1). Et ceci s'accorde fort bien avec nos expériences très exactes, dans lesquelles le moment final de la chute n'est pas discerné par le jugement des oreilles ou des yeux, dont ni l'un ni l'autre est ici assez sûr, mais où l'espace parcouru pendant la chute est trouvé sans erreur suivant une autre méthode que nous tâcherons d'exposer ici. La demi-oscillation d'un pendule suspendu à une paroi ou à une table dressée indique le temps de la chute. Pour que son globule soit lâché au même instant où on lâche le plomb qui doit exécuter la chute, les deux corps sont tenus reliés par un mince fil qui est rompu à l'aide d'une flamme. Mais avant cela on attache au plomb qui doit tomber un autre fil de longueur telle que lorsqu'il est tendu par la force du plomb tombant le pendule n'a pas encore atteint la paroi. L'autre extrémité de ce fil est attachée à une règle de papier, ou une mince membrane, glissant sur la paroi ou la table de telle manière qu'elle peut facilement suivre le poids tirant et descendre en ligne droite suivant sa longueur, en passant par l'endroit où le globe du pendule doit choquer la table. Toute la petite corde étant tendue, une partie de la règle est donc tirée en bas elle aussi par le plomb tombant, avant que le pendule a atteint la table. La grandeur de cette partie est indiquée par le globe qui est induit d'une légère couche de suie et met donc une marque sur la règle qui passe. En y ajoutant la longueur de la petite corde on a une mesure certaine de l'espace parcouru par le corps tombant. Dans ces considérations nous négligeons la résistance de l'air pour que la mesure qui convient aux corps tombants s'accorde entièrement avec les expériences. Et, certes, cette résistance n'est pas assez grande pour qu'elle puisse altérer sensiblement les résultats dans les hauteurs où l'on peut monter, pourvu que les corps soient supposés de métal ou bien de grandes dimensions s'ils consistent en une matière plus légère. En effet, la légèreté de la matière dans les corps qui traversent l'air en tombant est compensée de telle manière par la grandeur des corps qu'une sphère en bois ou | |||||||||||||||||||||||||||||||||||
[pagina 357]
| |||||||||||||||||||||||||||||||||||
quae nempe est pedis unciarum 18. Sicut autem quadrata temporum, ita sunt spatiaGa naar margenoot+ illis temporibus peracta, quemadmodum superiori propositione fuit ostensum. Ergo, si fiat ut quadratum ex 19‴ 1/10 ad quadratum ex 60‴, hoc est, ut 36481 ad 360000, ita 18 unciae ad aliud, fient ped. 14. unc. 9. lin. 6, altitudo descensus perpendicularis, tempore unius secundi. Cum autem pes Horarius sit ad Parisiensem, ut 881 ad 864; erit eadem altitudo, ad hanc mensuram reducta, proxime pedum 15 & unciae uniusGa naar voetnoot1). Atque haec cum accuratissimis experimentis nostris prorsus conveniunt. in quibus punctum illud temporis, quo casus finitur, non aurium aut oculi judicio discernitur; quorum neutrum hic satis tutum est; sed spatium descendendo peractum, alio modo, quem hic exponere tentabimus, absque ullo errore cognoscitur. Penduli, ad parietem tabulamve erectem, suspensi dimidia oscillatio moram temporis, cadendo adsumpti, indicat. Cujus sphaerula, ut eodem momento ac plumbum casui destinatum dimittatur, utraque filo tenui connexa tenentur, quod admoto igne inciditur. Sed prius, casuro plumbo, funiculus alius adnectitur, ejus longitudinis, ut, cum totus exierit à plumbo tractus, nondum ad pa|rietem illidatur pendulum. FuniculiGa naar margenoot+ ejus caput alterum, regulae chartaceae, aut ex tenui membrana paratae, cohaeret; ita ad parietem tabulamve applicatae, ut trahentem funem facile sequi possit, rectáque secundum longitudinem suam descendere; eo loci transiens, quo penduli sphaera ad tabulam accidet. Absumpto igitur funiculo toto, pars insuper regulae deorsum trahitur à cadente plumbo, priusquam pendulum ad tabulam pertingat. Quae quanta sit pars, sphaera fuligine leviter infecta, regulamque praeterlabentem signans, indicat. Huic autem addita funiculi longitudine, spatium cadendo emensum certò definitum habetur. Aëris autem occursum, quasi nullus esset in his intelligimus, ut mensura cadentibus corporibus praefixa cum experimentis exacte consentiat. Nec sane tantus est ille, ut in altitudinibus his, quò ascendere datur, sensibile discrimen inducere possit; dummodo solida corpora è metallo, aut, si leviore materia constent, mole grandiuscula accipiantur. Levitas enim materiae, in iis quae cadendo aërem secant, ita magnitudine corporis pensatur, ut sphaera lignea, vel etiam è subere formata, paria faciat cum plumbea: | |||||||||||||||||||||||||||||||||||
[pagina 358]
| |||||||||||||||||||||||||||||||||||
Ga naar margenoot+ même en liége va aussi vite qu'une sphère de plomb, lorsque les diamètres de ces sphères ont à ceux de la sphère de plomb le même rapport que la gravité spécifique du plomb à celle du bois ou du liége. En effet alors les gravités des sphères seront entre elles comme leurs surfacesGa naar voetnoot1). Toutefois, pour que les corps qui diffèrent beaucoup l'un de l'autre en gravité specifique tombent sensiblement avec une même viteffe, il n'est nullement nécessaire que cette proportion des diamàtres soit observée: les corps peuvent être égaux entre eux pourvu qu'ils soient l'un et l'autre assez grands ou qu'ils tombent d'une hauteur assez faible. Cependant il faut encore remarquer à ce propos que la hauteur peut être si grande ou bien (la hauteur étant faible) que la légèreté du corps projeté peut être telle qu'à cause de la résistance de l'air l'accélération du mouvement diffère énormément de celle que nous avons calculée plus haut. Car en général à chaque corps qui tombe à travers l'air ou un autre liquide correspond une vitesse déterminée, dépendant de son poids et de sa surface, qu'il ne peut jamais dépasser ou plutôt qu'il n'atteint jamais. C'est la vitesse que l'air, ou le liquide, devrait avoir vers le haut pour pouvoir soutenir le corps nageant dans lui. Mais nous aurons peut-être l'occasion de traiter ce sujet plus amplement en un autre endroitGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||
[pagina 359]
| |||||||||||||||||||||||||||||||||||
quando nimirumdiamet er harum ad plumbeae diametrum eam rationem habuerit, quamGa naar margenoot+ gravitas plumbi propria ad ligni suberisve gravitatem. Tunc enim gravitates sphaerarum erunt inter se sicut earum supersiciesGa naar voetnoot1). Veruntamen, ut aequali celeritate, quantum sensu percipi potest, decidant corpora, quae multum intrinseca gravitate differunt, nequaquam opus est ut proportio illa dimetrorum servetur. Possunt enim inter se aequalia esse, dummodo utraque satis magna sint; aut ex non nimia altitudine decidant. Etenim illud quoque hic animadvertendum est, tantam vel altitudinem esse posse; vel, in mediocri etiam altitudine, tantam projecti corporis levitatem; ut ob aëris renitentiam, acceleratio motus tandem ab illa, quam in superioribus demonstravimus, proportione plurimum recessura sit. Namque in universum, corpori cuilibet, per aërem aliudve liquidum labenti, certus celeritatis modus, pro ratione ponderis ac superficiei suae, constitutus est; quem excedere, aut potius ad quem pervenire nunquam possit. Quae nempe celeritas ea est, quam si aër, aut liquor ille sursum tendens, haberet, suspensum corpus idem sibi innatans sustinere posset. Verum de his, alias fortasse, pluribus agendi occasio eritGa naar voetnoot2). |
| ||||||||||||||||||||||||||||||||||