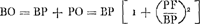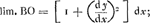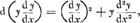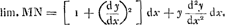Oeuvres complètes. Tome XVIII. L'horloge à pendule 1666-1695
(1934)–Christiaan Huygens–
[pagina 124]
| |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
Deuxième partie de l'horloge à pendule.
| |||||||||||||||||||||||||||||||
II.Mais maintenant il arrive par l'action de la gravité, de quelque cause qu'elle provienne, que les corps se meuvent d'un mouvement composé de leur mouvement uniforme dans une direction quelconque et de celui de haut en bas qui est dû à la gravité. | |||||||||||||||||||||||||||||||
III.On peut considérer ces deux mouvements séparément et l'un n'est pas empêché par l'autreGa naar voetnoot1).
Supposons qu'un corps pesant C, partant du repos, parcoure en un certain temps F, grâce à la force de la gravité, un espace CB [Fig. 23]. Supposons de plus que le même corps pesant ait reçu d'ailleurs un mouvement par lequel, s'il n'y avait aucune gravité, il parcourrait dans le même temps F d'un mouvement uniforme la ligne droite CD. La force de la gravité s'y ajoutant le corps pesant ne parviendra donc pas de C en D dans le dit temps F mais en un certain point E situé verticalement au-dessous de D de telle sorte que l'espace DE est toujours égal à l'espace CB; en effet, de cette façon le mouvement uniforme et celui qui provient de la gravité auront chacun leur part, l'un n'empêchant pas l'autre. Quant à la ligne que le corps parcourt de ce mouvement composé lorsque la direction du mouvement uniforme n'est pas verticale mais oblique, sa nature apparaîtra par nos considérations ultérieures. Mais lorsque le mouvement uniforme CD a lieu de haut en bas suivant une verticale, il est clair que la | |||||||||||||||||||||||||||||||
[pagina 125]
| |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
Horologii oscillatoriiGa naar margenoot+ Pars Secunda.
| |||||||||||||||||||||||||||||||
II.Nunc vero fieri gravitatis actione, undecunque illa oriatur, ut moveantur motu composito, ex aequabili quem habent in hanc vel illam partem, & ex motu deorsum à gravitate profecto.
composito, ex aequabili quem habent in hanc vel illam partem, & ex motu deorsum à gravitate profecto.
| |||||||||||||||||||||||||||||||
III.Et horum utrumque seorsim considerari posse, neque alterum ab altero impediriGa naar voetnoot1).
Ponatur grave C è quiete dimissum, certo tempore, quod dicatur F, vi gravitatis transire spatium CB [Fig. 23]. Ac rursus intelligatur idem grave accepisse alicunde motum quo, si nulla esset gravitas, transiret pari tempore F motu aequabili lineam rectam CD. Accedente ergo vi gravitatis non perveniet grave ex C in D, dicto tempore F, sed ad punctum aliquod E, recta sub D situm, ita ut spatium DE semper aequetur spario CB, ita enim, & motus aequabilis, & is qui à gravitate oritur suas partes peragent, altero alterum non impediente. Quamnam vero lineam, composito illo motu, grave percurrat, cum motus aequabilis non recta sursum aut deorsum sed in obliquum tendit, è sequentibus definiri poterit. Cum vero deorsum in perpendiculari contingit motus aequabilis CD, | apparetGa naar margenoot+ lineam CD, accedente motu ex gravitate, augeri | |||||||||||||||||||||||||||||||
[pagina 126]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ ligne CD est augmentée d'une droite DE par l'effet de la gravité. De même, lorsque le mouvement uniforme CD est dirigé de bas en haut, il est évident que la même longueur CD est diminuée de la longueur DE de sorte qu'après le temps F le corps se trouve toujours au point E. Que si, dans l'un et l'autre cas, nous considérons séparément les deux mouvements en admettant, comme nous l'avons dit, que l'un n'est nullement empêché par l'autre, il nous sera possible d'en déduire la cause et les lois de l'accélération des corps pesants. Premièrement nous ferons voir les deux choses suivantes. | |||||||||||||||||||||||||||||||
Proposition IGa naar voetnoot1).Dans des temps égaux les accroissements de la vitesse d'un corps tombant sont toujours égaux et les espaces parcourus durant des temps égaux depuis le commencement de la chute forment une série dont les différences successives sont constantes. 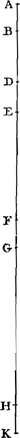 [Fig. 24.]
Supposons que quelque corps, partant du repos en A, soit tombé dans le premier temps par l'espace AB [Fig. 24] et ait acquis lorsqu'il est parvenu en B, une vitesse avec laquelle il pourrait ensuite pendant le deuxième temps parcourir d'un mouvement uniforme un certain espace BD. Nous savons donc que l'espace qui sera parcouru pendant le second temps sera plus grand que l'espace BD puisque, même si toute action de la pesanteur cessait en B, l'espace BD serait parcouru. Actuellement le corps sera animé d'un mouvement composé du mouvement uniforme par lequel il pourrait parcourir l'espace BD et du mouvement des corps tombants par lequel il doit nécessairement descendre d'une longueur égale à l'espace AB mentionné plus haut. Nous savons donc que le corps parviendra dans le deuxième temps jusqu'au point E, obtenu en ajoutant à BD une longueur DE égale à AB. Or, si nous demandons quelle vitesse le corps possède en E au bout du deuxième temps, nous trouverons qu'elle devra être double de la vitesse qu'il avait en B au bout du premier temps. En effet, nous avons dit que le corps se meut d'un mouvement composé d'un mouvement uniforme avec la vitesse acquise en B et du mouvement produit par la pesanteur; et ce dernier, étant évidemment le même dans le deuxième temps que dans le premier, doit avoir donné dans le cours du deuxième temps au corps pesant une vitesse égale à celle qu'il avait reçue à la fin du premier. Or, comme il a conservé intégralement la vitesse qu'il possédait à la fin du premier temps, il apparaît qu'à la fin du deuxième il possédera deux fois la vitesse acquise au bout du premier, en d'autres termes il aura une vitesse double. Que si, étant parvenu en E, le corps ne faisait autre chose que continuer son mouvement avec une vitesse uniforme, telle qu'il l'avait acquise en ce point, il apparaît que dans le troisième temps égal aux précédents, il parcourrait l'espace EF double de BD, puisque nous avons dit que ce dernier est parcouru avec une vitesse deux fois plus petite d'un mouvement uniforme et dans un temps égal. Mais lorsque | |||||||||||||||||||||||||||||||
[pagina 127]
| |||||||||||||||||||||||||||||||
recta DE. Item, cum sursum tendit motus aequabilis CD, ipsam CD diminui recta DE,Ga naar margenoot+ ut nempe, peracto tempore F, grave inveniatur semper in puncto E. Quod si, utroque hoc casu, seorfim, uti diximus, duos motus consideremus, alterumque ab altero nullo modo impediri cogitemus, hinc jam accelerationis gravium cadentium causam legesque reperire licebit. Et primum quidem duo ista simul ostendemus. | |||||||||||||||||||||||||||||||
Propositio IGa naar voetnoot1).AEqualibus temporibus aequales celeritatis partes gravi cadenti accrescere, & spatia aequalibus temporibus ab initio descensus emensa, augeri continue aequali excessu.
Ponatur grave aliquod, ex quiete in A, primo tempore lapsum esse per spatium AB [Fig. 24], atque ubi pervenit in B, acquisivisse celeritatem qua deinceps, tempore secundo, motu aequabili, percurrere posset spatium quoddam BD. Scimus ergo spatium secundo tempore peragendum majus fore spatio BD, quia vel cessante in B omni gravitatis actione spatium BD percurreretur. Feretur vero motu composito ex aequabili quo percursurum esset spatium BD, & ex motu gravium cadentium, quo deprimi necesse est per spa|tium ipsi AB aequale. Quare ad BD addita DE, aequali AB, scimusGa naar margenoot+ tempore secundo grave perventurum ad E. Quod si vero inquiramus quam velocitatem habeat in E, in fine secundi temporis, eam inveniemus duplam esse debere velocitatis quam habebat in B fine temporis primi. Diximus enim moveri composito motu ex aequabili cum celeritate acquisita in B, & ex motu à gravitate producto, qui cum tempore secundo idem plane sit ac primo, ideo decursu temporis secundi aequalem celeritatem gravi contulisse debet atque in fine primi. Quare cum acquisitam in fine primi temporis celeritatem conservaverit integram, apparet in fine secundi temporis bis eam celeritatem inesse quam acquisiverat in fine temporis primi, sive duplam. Quod si jam, postquam pervenit in E, pergeret deinceps tantum moveri celeritate aequabili, quantam illic acquisivit, apparet tempore tertio, prioribus aequali, percursurum spatium EF, quod duplum futurum sit spatii BD; quia hoc percurri diximus dimidia hujus celeritatis, motu aequabili, & temporis parte aequali. Accedente autem | |||||||||||||||||||||||||||||||
[pagina 128]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ l'action de la gravité s'y ajoute, il parcourra dans le troisième temps outre l'espace EF encore un espace FG égal à AB ou DE. Au bout du troisième temps le corps se trouvera donc en G. En ce point il aura une vitesse triple de celle qu'il avait en B au bout du premier temps, puisque outre la vitesse acquise en E dont nous avons dit qu'elle était le double de la vitesse acquise en B, la force de la gravité y a ajouté de nouveau dans la cours du troisième temps une vitesse égale à celle qu'elle lui avait donnée à le fin du premier temps. C'est pourquoi l'une et l'autre vitesse, au bout du troisième temps, constitueront ensemble une vitesse triple de celle qui existait à la fin du premier temps. On démontrera de la même manière que pendant le quatrième temps un espace GH triple de l'espace BD doit être parcouru, et simultanément un espace HK égal à AB; et que la vitesse en K au bout du quatrième temps sera quadruple de celle qui existait en B à la fin du premier. Ainsi il est manifeste que les espaces quelconques que nous pourrions considérer ensuite, nous voulons dire les espaces parcourus chacun dans un temps égal, croîtront d'une même différence égale à BD; et qu'en même temps les vitesses augmenteront uniformément chaque fois que le temps augmentera d'une même quantité. | |||||||||||||||||||||||||||||||
Proposition IIGa naar voetnoot1).L'espace parcouru pendant un certain temps par un corps qui commence sa chute en partant du repos est la moitié de l'espace que ce corps pourrait parcourir d'un mouvement uniforme avec la vitesse acquise par la chute au bout du temps considéré.
Faisons les mêmes hypothèses que dans le cas de la proposition précédente, où AB [Fig. 24] était l'espace parcouru pendant un certain temps par un corps tombant du point A, et BD l'espace qu'il était censé parcourir dans un temps égal avec une vitesse uniforme, savoir la vitesse acquise à la fin du premier temps, en d'autres termes au bout de l'espace AB. Je dis que l'espace BD est le double de AB. En effet, comme les espaces parcourus par le corps tombant pendant les quatre premiers temps égaux sont AB, BE, EG et GH, lesquels ont etre eux une certaine proportion, si nous prenons le double de chacun de ces temps, de sorte que nous considérons comme le premier temps les deux pendant lesquels les espaces AB, BE ont été parcourus, et comme le second les deux autres pendant lesquels furent parcourus les espaces EG, GK, il faut que les espaces AE et EK parcourus dans des temps égaux par un corps parti du repos, soient entre eux comme les espaces AB et BE également parcourus dans des temps égaux par un corps parti du repos. Comme on a donc AB : BE = AE : EK et, par conversion, KE : EA = EB (ou DA): AB, on aura aussi par division: DB est à BA comme la différence de KE et de EA est à EA. Or comme, d'après ce qui a été démontré dans la proposition précédente, KE est égal au double de AB augmenté du quintuple de BD, et que EA est égal tant au double de AB qu'à BD, il apparaît que la dite différence KE - EA est | |||||||||||||||||||||||||||||||
[pagina 129]
| |||||||||||||||||||||||||||||||
rursus gravitatis actione, percurret tempore tertio, praeter spatium EF, etiam spatiumGa naar margenoot+ FG, ipsi AB vel DE aequale. Itaque in fine tertii temporis grave invenietur in G. Velocitatem vero hic habebit triplam jam ejus quam habebat in B, in fine primi temporis: quia praeter celeritatem acquisitam in E, quam diximus duplam esse acquisitae in B, vis gravitatis, temporis tertii decursu, aequalem rursus atque in fine primi celeritatem contulit. Quamobrem utraque celeritas, in fine temporis tertii, triplam celeritatem constituet ejus quae fuerat in fine temporis primi. Eodem modo ostendetur tempore quarto peragi debere & spatium GH triplum spatii BD, & spatium HK ipsi AB aequale: velocitatemque in K, in fine quarti temporis, fore quadruplam ejus quae fuerat in B, in fine temporis primi. Atque ita spatia quotlibet deinceps considerata, quae aequalibus temporibus peracta fuerint, aequali excessu, qui ipsi BD aequalis sit, crescere manifestum est, simulque etiam velocitates per aequalia tempora aequaliter augeri. | |||||||||||||||||||||||||||||||
Propositio IIGa naar voetnoot1).Ga naar margenoot+Spatium peractum certo tempore à gravi, è quiete casum inchoante, dimidium est ejus spatii quod pari tempore transiret motu aequabili, cum velocitate quam acquisivit ultimo casus momento.
Ponantur quae in propositione praecedenti, ubi quidem AB [Fig. 24] erat spatium certo tempore, à gravi cadente ex A, peractum. BD vero spatium quod pari tempore transiri intelligebatur celeritate aequabili, quanta acquisita erat in fine primi temporis, seu in fine spatii AB. Dico itaque spatium BD duplum esse ad AB. Quum enim spatia primis quatuor aequalibus temporibus à cadente transmissa sint AB, BE, EG, GH, quorum inter se certa quaedam est proportio: si eorum temporum dupla tempora sumamus, ut nempe pro primo tempore jam accipiantur duo illa quibus spatia AB, BE, peracta fuere; pro secundo vero tempore duo reliqua quibus peracta fuere spatia EG, GK, oportet jam spatia AE, EK, quae sunt aequalibus temporibus à quiete peracta, inter se esse sicut spatia AB, BE, quae aequalibus item temporibus à quiete percurrebantur. Quum igitur sit ut AB ad BE, ita AE ad EK; & convertendo, ut EB sive DA ad AB ita KE ad EA: erit quoque, dividendo, DB ad BA ut excessus KE supra EA ad EA. Quum sit autem, ex ostensis propositione praecedenti, KE aequalis tum duplae AB, tum quintuplae BD: EA vero aequalis tum duplae AB, tum simplici BD; apparet dictum excessum KE supra EA aequari quadruplae BD. Sicut igitur DB ad BA ita erit | |||||||||||||||||||||||||||||||
[pagina 130]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ égale à quatre fois BD. Donc DB : BA = 4DB : EA. Par conséquent on aura EA = 4BA. Mais le même espace EA est égal, comme nous l'avons dit, au double de AB augmenté de BD. BD est donc égal au double de AB. C. Q. F. D. | |||||||||||||||||||||||||||||||
Proposition III.Deux espaces parcourus par un corps tombant dans des temps quelconques, dont chacun est pris depuis le commencement de la chute, sont entre eux comme les carrés de ces temps, ou bien comme les carrés des vitesses acquises. 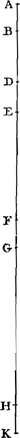 [Fig. 24.]
En effet, comme il a été démontré dans la proposition précédente que les espaces AB, BE, EG et GK [Fig. 24] en nombre quelconque, parcourus dans des temps égaux par un corps tombant, croissent par un excès égal, lequel a la valeur BD; il apparaît maintenant, puisque BD = 2AB, qu'on aura BE = 3AB, EG = 5AB, GK = 7AB, et qu'en général les espaces parcourus augmenteront suivant la série des nombres impairs à partir de l'unité 1, 3, 5, 7, 9, etc.; et comme un nombre quelconque de ces valeurs prises consécutivement font un carré dont le côté est égal à ce nombre quelconque lui-même (p.e. la somme des trois premières est neuf, celle des quatre premières seize, etc.), il s'ensuit que les espaces parcourus par un corps tombant et pris chacun à partir du commencement de la chute, sont entre eux en raison double des temps de chute, bien entendu si l'on prend des temps commensurables. Or, la démonstration peut aisément être étendue aux temps incommensurables eux aussi. En effet, considérons des temps de ce genre ayant entre eux un rapport égal à celui des longueurs AB et CD [Fig. 25] et soient E et F les espaces parcourus dans ces temps pris l'un et l'autre depuis le commencement de la chute. Je dis que l'espace E sera à l'espace F comme le carré de AB est à celui de CD. Car si cela est nié: que l'espace E ait d'abord à l'espace F un rapport supérieur à celui de AB2 à CD2, savoir celui de AB2 à CG2, CG étant pris inférieur à CD. Qu'on ôte de CD la partie DH moindre que DG - CG et telle que le reste HC soit commensurable avec AB; car il est certain que ceci est possible. On aura donc CH > CG. Mais comme le carré du temps AB est à celui du temps CH, ainsi est l'espace E parcouru pendant le temps AB à l'espace parcouru pendant le temps CH, d'après ce qui a été démontré plus haut. Mais l'espace F, parcouru pendant le temps CD, est plus grand que celui parcouru pendant le temps CH. Or, E : F = AB2 : CG2 par hypothèse; par conséquent le rapport AB2 : CG2 sera aussi inférieur au rapport AB2 : CH2; il en résulte que le carré de CG | |||||||||||||||||||||||||||||||
[pagina 131]
| |||||||||||||||||||||||||||||||
quadrupla DB ad EA: unde EA quadrupla erit ipsius BA: eadem vero EA aequatur,Ga naar margenoot+ uti diximus, & duplae AB & simplici BD. ergo BD duplae AB aequalis erit; quod erat demonstrandum. | |||||||||||||||||||||||||||||||
Propositio III.Ga naar margenoot+Spatia duo, à gravi cadente quibusllibet temporibus transmissa, quorum utrumque ab initio descensus accipiatur, sunt inter se in ratione duplicata eorundem temporum, sive ut temporum quadrata, sive etiam ut quadrata celeritatum in fine cujusque temporis acquisitarum.
sive ut temporum quadrata, sive etiam ut quadrata celeritatum in fine cujusque temporis acquisitarum.
Quum enim ostensum sit propositione antecedenti spatia AB, BE, EG, GK [Fig. 24], quotcunque fuerint, aequalibus temporibus à cadente, peracta, crescere aequali excessu, qui excessus sit ipsi BD aequalis: Patet nunc, quoniam BD est dupla AB, spatium BE fore triplum AB; EG quintuplum ejusdem AB; GK septuplum; aliaque deinceps auctum iri secundum progressionem numerorum imparium ab unitate, 1, 3, 5, 7, 9, &c. cumque quotlibet horum numerorum, sese consequentium, summa faciat quadratum, cujus latus est ipsa adsumptorum numerorum multitudo (velut si tres primi addantur, facient novem, si quatuor sexdecim) sequitur hinc spatia, à gravi cadente transmissa, quorum utrumque à principio casus inchoetur, esse inter se in ratione duplicata temporum quibus casus duravit, si nempe tempora commensurabilia sumantur. Facile autem & ad tempora incommensurabilia demonstratio extendetur. Sint enim tempora hujusmodi, quorum inter se ratio ea quae linearum AB, CD [Fig. 25]. spatiaque temporibus his transmissa sint E, & F, utraque nimirum ab initio descensus adsumpta. Dico esse, ut quadratum AB ad quadratum CD, ita spatium E ad F. Si enim negetur; habeat primo, si potest, spatium E ad F majorem rationem quam quadratum AB ad quadratum CD, nempe eam quam quadratum AB ad quadratum CG, sumta CG minore quam CD, & à CD auferatur pars DH, minor quam DG excessus CD supra CG, atque ita ut reliqua HC commensurabilis sit ipsi AB; hoc enim fieri posse constat. Erit ergo CH major quam CG. Atqui ut quadratum temporis AB ad quadratum temporis CH, ita spatium E, quod tempore AB peractum est, ad spatium peractum tempore CH, per superius ostensa. Hoc vero spatio majus est illud quod tempore CD percurritur, nempe spatium F. ergo spatii E ad spatium F minor est ratio quam quadratri AB ad quadratum CH. Sicut autem spatium E ad F, ita ponebatur esse quadratum AB ad quadratum CG, ergo minor quoque erit ra|tio quadratiGa naar margenoot+ AB ad quadratum CG, quam quadrati AB ad quadratum CH, | |||||||||||||||||||||||||||||||
[pagina 132]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ est plus grand qu le carré de CH, ce qui est absurde puisque nous avons posé CH > CG. Ainsi le rapport E : F n'est pas supérieur à AB2 : CD2. Qu'il lui soit donc inférieur, si cela se peut; et soit le rapport de l'espace E à l'espace F le même que celui du carré AB au carré CL, CL étant pris plus grand que CD. Ôtons de CL LK, plus petit que LD, c.à.d. que CL - CD, de telle manière que le reste KC soit commensurable avec AB. Comme l'espace E, parcouru dans le temps AB, est à l'espace parcouru dans le temps CK comme le carré du temps AB est au carré du temps CK, mais que l'espace F parcouru dans le temps CD est inférieur à l'espace parcouru dans le temps CK, le rapport de l'espace E à l'espace F sera supérieur à AB2 : CK2. Mais E : F = AB2 : CL2 par hypothèse. Donc AB2 : CL2 > AB2 : CK2, et par conséquent CL2 < CK2. Ce qui est absurde, puisque CL > CK. Par conséquent il est également faux de dire que E : F < AB2 : CD2. Il est donc nécessaire que ces deux rapports soient égaux. Enfin, attendu que les vitesses acquises au bout des temps AB et CD sont entre elles comme ces temps, il apparaît que le rapport des espaces E et F est aussi le même que celui des carrés des temps AB et CD pendant lesquels ils ont été parcourus. La proposition est donc démontrée. | |||||||||||||||||||||||||||||||
Proposition IVGa naar voetnoot1).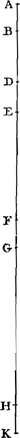 [Fig. 24.]
Lorsqu'un corps pesant aura commencé à tendre vers le haut avec la vitesse acquise à la fin de sa chute, il arrivera qu'il parcourra dans des temps égaux en remontant les espaces parcourus d'abord en descendant et qu'il s'élèvera de cette façon jusqu'à la hauteur dont il était tombé. De plus il arrivera qu'en des parties égales de temps il perdra des quantités égales de vitesse.
En effet, que l'on considère, comme dans le cas de la Prop. II, des espaces en nombre quelconque parcourus en tombant depuis le repos dans d'égales durées de temps, dont l'espace AB [Fig. 24] soit le premier, et dont le deuxième soit la somme de BD, qui pourrait être parcouru uniformément avec la vitesse acquise par la chute AB, et de DE égal à AB, tandis que le troisième est la somme de EF, double de BD, et de FG, égal à AB; le quatrième la somme de GH = 3BD et de HK de nouveau égal à AB, et ainsi de suite s'il y en a encore davantage. Je dis que lorsque le corps remonte, il devra parcourir de nouveau les espaces KG, GE, EB, BA dans des temps égaux aux temps respectifs de la descente, en commençant son ascension avec la vitesse qu'il avait acquise à la fin de la chute au point K. Pour être plus court, je désignerai de nouveau chaque vitesse par la longueur de l'espace que le corps pourrait parcourir avec cette vitesse dans un élément de temps pareil à ceux considérés dans le cas de la descente. D'aprés ce qui a été démontré dans la proposition précédente, le corps, lorsqu'il est parvenu en K, possède une vitesse GH + BD ou KF, puisque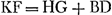 ; en effet, les parties HK et FG sont l'une et l'autre égales à AB et ; en effet, les parties HK et FG sont l'une et l'autre égales à AB et
| |||||||||||||||||||||||||||||||
[pagina 133]
| |||||||||||||||||||||||||||||||
ac proinde quadratum CG majus quadrato CH; quod est absurdum, quum CH majorGa naar margenoot+ dicta sit quam CG. Non habet igitur spatium E ad F majorem rationem quam quadratum AB ad quadratum CD. Habeat jam, si potest, minorem; sitque ratio spatii E ad F eadem quae quadrati AB ad quadratum CL, sumptâ CL majore quam CD, & à CL auferatur LK minor excessu LD, quo CD superatur à CL, atque ita ut reliqua KC sit commensurabilis AB. Quia ergo ut quadratum temporis AB ad quadratum temporis CK, ita est spatium E, peractum tempore AB, ad spatium peractum tempore CK. Hoc vero spatio minus est spatium peractum tempore CD, nempe spatium F. erit proinde spatii E ad F major ratio quam quadrati AB ad quadratum CK. Sicut autem spatium E ad F, ita ponebatur esse quadratum AB ad quadratum CL. Ergo major erit ratio quadrati AB ad quadratum CL quam ejusdem quadratri AB ad quadratum CK, ideoque quadratum CL minus erit quam qu. CK. quod est absurdum, quum CL major sit quam CK. Ergo neque minorem rationem habet spatium E ad F quam quadratum AB ad quadratum CD. quare necesse est ut eandem habeat. Porro cum celeritates in fine temporum AB, CD acquisitae sint inter se sicut ipsamet tempora; apparet rationem spatiorum E ad F eandem quoque esse quae quadratorum temporum AB, CD, quibus transmissa sunt. Itaque constat propositum. | |||||||||||||||||||||||||||||||
Propositio IVGa naar voetnoot1).Si grave celeritate ea quam in fine descensus acquisivit sursum tendere caeperit, fiet ut paribus temporis partibus, spatia quae prius sursum, eadem deorsum transeat, adeoque ad eandem unde descenderat altitudinem ascendat. Item ut aequalibus temporis partibus aequalia amittat celeritatis momenta.
Sunto enim ut in propositione 2, spatia quotlibet, aequalibus | temporis partibusGa naar margenoot+ cadendo è quiete peracta, quorum primum AB [Fig. 24]; secundum compositum ex BD, quod celeritate aequabili acquisita per AB transeundum erat, & ex DE ipsi AB aequali; tertium compositum, ex EF, duplo ipsius BD, & ex FG, eidem AB aequali; quartum compositum ex GH, triplo ipsius BD, & ex HK ipsi itidem AB aequali, atque eadem ratione porro crescentia, si plura fuerint. Dico totidem aequalibus temporibus eadem spatia KG, GE, EB, BA, singula singulis peragenda esse à gravi sursum tendente, atque incipiente cum celeritate in fine descensus K acquisita. Brevitatis autem gratia celeritas quaeque designetur deinceps longitudine spatii quod grave motu aequabili, cum celeritate illa, atque temporis parte una, quales in descensu consideravimus, transmissurum esset. Itaque ex ostensis dicta propositione, cum in K grave pervenerit, habet celeritatem GH auctam celeritate BD, hoc est celeritatem KF, quia KF aequatur ipsis HG, BD, sunt enim partes singulae HK, FG, aequales ipsi AB, ac proinde utraque simul ipsi BD, | |||||||||||||||||||||||||||||||
[pagina 134]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ par conséquent leur somme est égale à BD, que nous avons démontré dans la Prop. II être le double de AB. Par conséquent si au bout de la chute le corps, invertissant la vitesse verticale acquise en K, s'élevait d'un mouvement uniforme, il parcourrait l'espace KF en un élément de temps. Mais, puisque l'action de la gravité s'en mêle, son ascension KF sera diminuée d'un espace FG égal à AB, comme cela ressort de l'énoncé d'une de nos hypothèses initiales. Pendant le premier élément de temps le corps ne montera donc qu'à la hauteur KG dont il était descendu dans l'élément de temps précédent. Mais il est nécessaire qu'en même temps la vitesse ait diminué de BD, qui est la vitesse acquise par une chute d'un élément de temps. Lorsque le corps sera remonté jusqu'en G, il lui reste donc une vitesse HG, puisqu'au début de l'ascension il possédait une vitesse HG + BD. Or GD = HG, puisque  . Par conséquent, si le corps montait de G d'un mouvement uniforme avec la vitesse qu'il possède en ce point. il parcourrait l'espace GD en un élément de temps. Mais grâce à l'action de la pesanteur cette hauteur sera diminuée de l'espace DE égal à AB. Pendant le deuxième élément de temps le corps s'élèvera donc d'un espace GE, le même qu'il avait parcouru en tombant dans un élément égal de temps. En même temps il faut qu'il ait perdu de nouveau une partie de sa vitesse égale à celle qui correspond à une chute d'un élément de temps, savoir la
vitesse BD. Lorsqu'il se sera
élevé jusqu'en E, il a donc la vitesse FE qui est égale à la différence GD - BD. Car BD, comme nous l'avons déjà dit, est égale a la somme DE + FG.
Or, on a FE = EA, puisque FE = 2BD, en d'autres termes . Par conséquent, si le corps montait de G d'un mouvement uniforme avec la vitesse qu'il possède en ce point. il parcourrait l'espace GD en un élément de temps. Mais grâce à l'action de la pesanteur cette hauteur sera diminuée de l'espace DE égal à AB. Pendant le deuxième élément de temps le corps s'élèvera donc d'un espace GE, le même qu'il avait parcouru en tombant dans un élément égal de temps. En même temps il faut qu'il ait perdu de nouveau une partie de sa vitesse égale à celle qui correspond à une chute d'un élément de temps, savoir la
vitesse BD. Lorsqu'il se sera
élevé jusqu'en E, il a donc la vitesse FE qui est égale à la différence GD - BD. Car BD, comme nous l'avons déjà dit, est égale a la somme DE + FG.
Or, on a FE = EA, puisque FE = 2BD, en d'autres termes  . Par conséquent si le corps continuait à monter à partir de E d'un mouvement uniforme avec la vitesse qu'il a en ce point, il parcourrait l'espace EA en un élément de temps. Mais puisque la gravité exerce son action, cette hauteur sera diminuée de l'espace AB. Par conséquent pendant cet élément de temps il ne montera que d'une hauteur EB, espace qu'il avait aussi parcouru en descendant dans un élément égal de temps. En ce moment il doit nécessairement avoir perdu de nouveau une vitesse telle qu'il pourrait l'acquérir en tombant durant un élément de temps, c.à.d. la vitesse BD. Par conséquent le corps arrivé en B a pour reste de vitesse la vitesse BD, tandis qu'en E il avait la vitesse FE double de BD. S'il continuait donc à monter à partir de B avec une vitesse constante telle qu'il la possède en ce point, il parcourrait en un élément de temps un espace égal à DB ou 2AB. Mais par l'effet de la gravité cette hauteur est diminuée d'un espace égal à AB. Pendant cet élément de temps le corps ne montera donc que de BA qu'il avait aussi parcouru en descendant pendant le premier élément de temps. Et à la fin du dernier élément de temps considéré ici le corps se trouvera nécessairement au point A. Mais quelqu'un dira peut-être qu'il s'est élevé plus haut que le point A et est retombé à partir de là. Ceci toutefois serait absurde puisqu'il ne peut, par un mouvement dû à la gravité, monter à une plus grande hauteur que celle dont il était descendu. D'ailleurs comme de la vitesse qu'il
avait en B la portion BD a été
anéantie, il est évident que lorsque le corps atteignait . Par conséquent si le corps continuait à monter à partir de E d'un mouvement uniforme avec la vitesse qu'il a en ce point, il parcourrait l'espace EA en un élément de temps. Mais puisque la gravité exerce son action, cette hauteur sera diminuée de l'espace AB. Par conséquent pendant cet élément de temps il ne montera que d'une hauteur EB, espace qu'il avait aussi parcouru en descendant dans un élément égal de temps. En ce moment il doit nécessairement avoir perdu de nouveau une vitesse telle qu'il pourrait l'acquérir en tombant durant un élément de temps, c.à.d. la vitesse BD. Par conséquent le corps arrivé en B a pour reste de vitesse la vitesse BD, tandis qu'en E il avait la vitesse FE double de BD. S'il continuait donc à monter à partir de B avec une vitesse constante telle qu'il la possède en ce point, il parcourrait en un élément de temps un espace égal à DB ou 2AB. Mais par l'effet de la gravité cette hauteur est diminuée d'un espace égal à AB. Pendant cet élément de temps le corps ne montera donc que de BA qu'il avait aussi parcouru en descendant pendant le premier élément de temps. Et à la fin du dernier élément de temps considéré ici le corps se trouvera nécessairement au point A. Mais quelqu'un dira peut-être qu'il s'est élevé plus haut que le point A et est retombé à partir de là. Ceci toutefois serait absurde puisqu'il ne peut, par un mouvement dû à la gravité, monter à une plus grande hauteur que celle dont il était descendu. D'ailleurs comme de la vitesse qu'il
avait en B la portion BD a été
anéantie, il est évident que lorsque le corps atteignait
| |||||||||||||||||||||||||||||||
[pagina 135]
| |||||||||||||||||||||||||||||||
quam esse duplam AB ostendimus propositione 2. Itaque celeritatem in fine descensusGa naar margenoot+ K acquisitam sursum convertendo, si grave aequabili motu ferretur, conficeret una temporis parte spatium KF. Atqui, gravitatis actione accedente, diminuetur ascensus KF spatio FG ipsi AB aequali, ut patet ex dictis ad hypothesin initio sumptam. Ergo parte prima temporis ascendet grave tantum per KG, quo eodem spatio parte temporis novissima descenderat. Simul vero & celeritati tantum decessisse necesse est, quantum acquiritur temporis parte una deorsum cadendo, hoc est celeritatem BD. Itaque grave, ubi ad G ascenderit, habet celeritatem reliquam HG, cum initio ascensus habuerit celeritatem HG una cum celeritate BD. Est autem ipsi HG aequalis GD; quum aequetur ipsi FE una cum DB, hoc est una cum dupla AB, hoc est una cum duabus FG & ED; Ergo si ex G, cum celeritate aequabili, quantam illic habet, sursum pergeret, conficeret una parte temporis spatium GD. Accedente autem gravitatis actione, diminuetur ascensus iste spatio DE, ipsi AB aequali. Ergo, hac secunda parte temporis, ascendet per spatium GE, quod simili temporis parte etiam cadendo transierat. Simul autem celeritate tantum decessisse denuo debet quantum temporis parte una ex casu acquiritur; nempe celeritas BD. Itaque ubi usque ad|E ascenderit, habetGa naar margenoot+ duntaxat celeritatem FE, quae nimirum relinquitur quum à celeritate GD aufertur celeritas BD. Nam BD, ut jam diximus, aequalis est duabus DE, FG. Est autem ipsi FE aequalis EA, quum FE aequetur ipsi BD bis sumptae, hoc est ipsi BD una cum dupla AB, hoc est una cum duabus AB, DE. Ergo si ex E cum celeritate aequabili, quantam illic habet, sursum pergeret, confecturum esset una temporis parte spatium EA. Sed accedente actione gravitatis, diminuetur ascensus iste ipso spatio AB. Proinde hac parte temporis per spatium EB tantum ascendet, quod simili parte temporis descendendo quoque transierat. Hic vero rursus celeritati tantum decessisse necesse est quantum una temporis parte cadendo deorsum acquiritur, hoc est celeritatem BD. Itaque grave, ubi usque ad B ascenderit, habet celeritatem ipsam BD reliquam, cum in E habuerit celeritatem FE ipsius BD duplam. Si ergo ex B cum celeritate aequabili, quantam illic habet, sursum pergeret, confecturum esset parte una temporis spatium aequale ipsi DB, hoc est duplum AB. Sed accedente gravitatis actione, diminuitur ascensus iste spatio quod ipsi AB aequale sit. Igitur hac parte temporis ascendet tantummodo per spatium BA, quod etiam primo descensus tempore transierat. Atque in fine quidem extremi temporis hujus necessario grave in A puncto reperietur. Sed dicetur forsan altius ascendisse quam ad A, atque inde eo relapsum esse. At hoc absurdum esset, cum non possit, motu à gravitate profecto, altius quam unde decidit ascendere. Porro quum celeritati quam in B habebat rursus decesserit celeritas BD, | |||||||||||||||||||||||||||||||
[pagina 136]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ A il ne lui restait aucune vitesse et que par conséquent il n'a pu s'élever plus haut. Il est donc démontré qu'il est parvenu à la hauteur même dont il était tombé et qu'il a de nouveau parcouru chacun des divers espaces (qu'il avait traversés en descendant en des éléments de temps égaux entre eux) dans des temps d'ascension de même durée; et il s'est montré de plus que dans des éléments égaux de temps il a perdu des quantités égales de vitesse. La proposition est donc prouvée.
Or, comme il a été admis dans la démonstration de la Prop. II, dont la proposition précédente dépend, qu'il existe un rapport déterminé entre les espaces parcourus par un corps tombant dans des temps consécutifs égaux, et que ce rapport est le même quels que soient les temps égaux considérés - ce qui doit être ainsi d'après la nature du phénomène et, si on voulait le nier, il faudrait avouer que la recherche du rapport de ces espaces est vaineGa naar voetnoot1) - cependant, comme la proposition peut aussi être démontrée sans ce prémice, en suivant la méthode de Galilée, il sera utile de formuler ici plus correctement la démonstration qu'il a donnée dans une forme moins parfaiteGa naar voetnoot2). Nous démontrerons donc de nouveau la | |||||||||||||||||||||||||||||||
Proposition V.L'espace parcouru pendant un certain temps par un corps qui commence sa chute en partant du repos est la moitié de l'espace que ce corps pourrait parcourir d'un mouvement uniforme avec la vitesse acquise par la chute au bout du temps considéré.
Soit AH [Fig. 26] le temps de la chute entière; puisse le mobile avoir parcouru en ce temps une distance dont le plan P indique la grandeur. De plus, en tirant HL, de longueur quelconque, perpendiculairement à AHGa naar voetnoot3), nous admettons que cette lon- | |||||||||||||||||||||||||||||||
[pagina 137]
| |||||||||||||||||||||||||||||||
patet jam gravi in A constituto nullam celeritatem superesse, ac proinde non altiusGa naar margenoot+ excursurum. Itaque ostensum est ad eandem unde decidit altitudinem pervenisse, & singula spatia, quae aequalibus descensus temporibus transmiserat, eadem totidem ascensus temporibus remensum esse: sed & aequalibus temporibus aequalia ipsi decessisse celeritatis momenta apparuit. Ergo constat propositum. 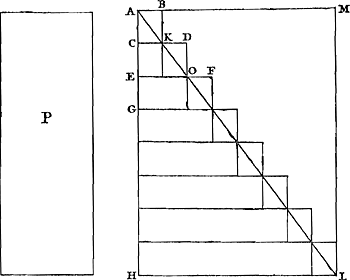 [Fig. 26.]
Quia vero in demonstratione propositionis secundae, ex qua pendet praecedens, adsumptum fuit certam quandam esse proportionem spatiorum quae continuis aequalibus temporibus à gravi cadente transeuntur, quaeque eadem sit, quaecunque aequalia tempora accipiantur; quod quidem & ex rei natura ita se habere necesse est, & si negetur, fatendum frustra proportionem istorum spatiorum investigariGa naar voetnoot1). Tamen, quia propositum etiam absque hoc demonstrari potest, Galilei methodum sequendo, | operae pretiumGa naar margenoot+ erit demonstrationem, ab illo minus perfecte traditamGa naar voetnoot2), hic accuratius conscribere. itaque rursum hic demonstrabimus. | |||||||||||||||||||||||||||||||
Propositio V.Spatium peractum certo tempore, à gravi è quiete casum inchoante, dimidium esse ejus spatii quod pari tempore transiret motu aequabili, cum celeritate quam acquisivit ultimo casus momento.
Sit tempus descensus totius AH [Fig. 26], quo tempore mobile peregerit spatium quoddam cujus quantitas designetur plano P. ductaque HL perpendiculari ad AHGa naar voetnoot3), | |||||||||||||||||||||||||||||||
[pagina 138]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ gueur-là représente la vitesse acquise au bout de la chute. Complétant ensuite le rectangle AHLM, nous entendons représenter par lui la grandeur de l'espace qui serait parcouru dans le temps AH avec la vitesse HL. Il faut donc démontrer que le plan P est la moitié du rectangle MH, en d'autres termes, lorsqu'on tire la diagonale AL, qu'il est égal au triangle AHL. Si le plan P n'est pas égal au triangle AHL, il sera donc ou plus petit ou plus grand. Supposons d'abord, si la chose est possible, le plan P inférieur au triangle AHL. Divisons AH en autant de parties égales AC, CE, EG etc. que - lorsque nous circonscrivons au triangle AHL une figure composée de rectangles dont la hauteur soit égale à la longueur de chacune de ces parties de AH, tels que les rectangles BC, DE et FG, et que nous inscrivons dans le même triangle une deuxième figure composée de rectangles de la même hauteur tels que KE, OG, etc. - l'excès de la première figure sur la deuxième soit moindre que celui du triangle AHL sur le plan P. En effet, il est évident que ceci est possible, puisque l'excès total de la figure circonscrite sur la figure inscrite est égal à un très petit rectangle ayant HL pour base. Conséquemment l'excès du triangle AHL sur la figure inscrite sera certainement moindre que son excès sur le plan P; la figure inscrite au triangle sera donc plus grande que le plan P. D'autre part, comme la droite AH représente le temps de la chute totale, ses parties égales AC, CE, EG représenteront des parties égales de ce temps. Or, puisque les vitesses du mobile tombant croissent dans le même rapport que les temps de chute,Ga naar margenoot* et que la vitesse acquise à la fin du temps entier est HL, la vitesse acquise au bout de la première partie AC du temps sera CK, parce que AH : AC = HL : CK. Pareillement la vitesse acquise au bout de la deuxième partie CE du temps, sera ED et ainsi de suite. Il est évident que pendant le premier temps AC un certain espace supérieur à zéro a été traversé par le mobile, et que pendant le deuxième temps CE un espace supérieur à KE a été parcouru, puisque l'espace KE eût été parcouru dans le temps CE d'un mouvement uniforme avec la vitesse CK. En effet, les espaces parcourus uniformément ont entre eux un rapport composé du rapport des temps et de celui des vitesses; par conséquent, puisque nous avons admis que l'espace MH est parcouru dans le temps AH avec la vitesse constante HL, il s'ensuit que l'espace KE est parcouru dans le temps CE avec la vitesse CK, attendu que le rapport du rectangle MH au rectangle KE est composé des rapports AH : CE et HL : EOGa naar voetnoot1). Comme l'espace KE, ainsi que je l'ai dit, est donc celui qui serait parcouru dans se temps CE avec la vitesse uniforme CK, et que le mobile est transporté durant le temps CE d'un mouvement accéléré qui avait déjà au début de ce temps la vitesse CK, il est manifeste que par ce mouvement accéléré le mobile parcourra dans le temps CE un espace supérieur à KE. Pour la même raison il traversera pendant le troisième temps EG une distance supérieure à OG: car c'est OG qu'il parcourrait dans ce même temps EG avec la vitesse uniforme EO. Et ainsi de suite, dans chacune des parties du temps AH, le mobile parcourra un espace supérieur au rectangle correspondant de la figure inscrite. C'est pourquoi l'espace entier parcouru d'un mouvement accéléré sera plus | |||||||||||||||||||||||||||||||
[pagina 139]
| |||||||||||||||||||||||||||||||
longitudinis cujuslibet, referat illa celeritatem in fine casus acquisitam. Deinde completoGa naar margenoot+ rectangulo AHLM, intelligatur eo notari quantitas spatii quod percurreretur tempore AH, cum celeritate HL. Ostendendum est igitur planum P dimidium esse rectanguli MH, hoc est, ducta diagonali AL, aequale triangulo AHL. Si planum P non est aequale triangulo AHL, ergo aut minus eo erit, aut majus. Sit primo, si fieri potest, planum P minus triangulo AHL. dividatur autem AH in tot partes aequales AC, CE, EG &c. ut, circumscriptâ triangulo AHL figurâ è rectangulis quorum altitudo singulis divisionum ipsius AH partibus aequetur, ut sunt rectangula BC, DE, FG, alterâque eidem triangulo inscriptâ, ex rectangulis ejusdem altitudinis, ut sunt KE, OG &c. ut, inquam, excessus illius figurae supra hanc, minor sit excessu | trianguli AHL supra planum P. hoc enim fieri posse perspicuum est, cum totusGa naar margenoot+ excessus figurae circumscriptae super inscriptam aequetur rectangulo infimo, basin habenti HL. Erit itaque omnino excessus ipsius trianguli AHL supra figuram inscriptam minor quam supra planum P, ac proinde figura triangulo inscripta major plano P. Porro autem, quum recta AH tempus totius descensus referat, ejus partes aequales AC, CE, EG, aequales temporis illius partes referent. Cumque celeritates mobilis cadentis crescant eadem proportione qua tempora descensusGa naar margenoot*; sitque celeritas in fine totius temporis acquisita HL; erit ea, quae in fine primae partis temporis AC acquiretur, CK; quia ut AH ad AC, ita HL ad CK. Similiter quae in fine partis temporis secundae CE acquiritur, erit EO, atque ita deinceps. Patet autem, tempore primo AC, spatium aliquod à mobili transmissum esse, quod majus sit nihilo; tempore vero secundo CE transmissum esse spatium quod majus sit quam KE, quia spatium KE transmissum fuisset tempore CE, motu aequabili, cum celeritate CK. habent enim spatia, motu aequabili transacta, rationem compositam ex ratione temporum, & ratione velocitatum, ideoque cum tempore AH, celeritate aequabili HL percurri posuerimus spatium MH, sequitur tempore CE, cum celeritate CK, percurri spatium KE, quum ratio rectanguli MH ad rectangulum KE componatur ex rationibus AH ad CE, & HL ad EOGa naar voetnoot1). Quum ergo, ut dixi, spatium KE sit illud quod transmitteretur tempore CE, cum celeritate aequabili CK, mobile autem feratur tempore CE motu accelerato, qui jam principio hujus temporis habet celeritatem CK; manifestum est isto accelerato motu, tempore CE, majus spatium quam KE confecturum. Eadem ratione, tempore tertio EG, majus spatium conficiet quam OG, quia nempe hoc confecturum esset tempore eodem EG, cum celeritate aequabili EO. Atque ita deinceps, singulis temporis AH partibus, à mobili majora spatia quam sunt rectangula figurae inscriptae, ipsis partibus | |||||||||||||||||||||||||||||||
[pagina 140]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ grand que la figure inscrite. Or, cet espace fut posé égal au plan P. Par conséquent la figure inscrite sera plus petite que l'espace P, ce qui est absurde, car il a été démontré qu'elle lui est supérieure. Le plan P n'est donc pas inférieur au triangle AHL. Nous ferons voir qu'il ne lui est pas non plus supérieur. En effet, qu'il le soit, si cela est possible. Divisons AH en parties égales et supposons de nouveau, comme précédemment, qu'au triangle AHL soit inscrit et circonscrit une figure composée de rectangles, de telle manière que l'une surpasse l'autre d'un excès inférieur à celui du plan P sur le triangle AHL. La figure circonscrite sera donc nécessairement inférieur au plan P. Il est évident d'abord que pendant la première partie AC du temps un espace inférieur à BC est traversé par le mobile, puisque ce dernier serait parcouru dans le même temps AC avec une vitesse uniforme CK, vitesse que le mobile ne possède qu'à la fin du temps AC. De la même manière dans la deuxième partie CE du temps un espace inférieur à DE sera parcouru du mouvement accéléré, puisque DE serait parcouru dans le même temps CE avec la vitesse constante EO que le mobile n'atteint qu'à la fin du temps CE. Et ainsi de suite dans chacune des parties du temps AH il sera parcouru par le mobile un espace inférieur au rectangle correspondant de la figure circonscrite. C'est pourquoi l'espace total parcouru d'un mouvement accéléré sera moindre que la figure circonscrite entière. Or, cet espace fut posé égal au plan P; par conséquent le plan P sera aussi inférieur à la figure circonscrite. Ce qui est absurde, attendu qu'il a été démontré que cette figure est plus petite que le plan P. Par conséquent le plan P n'est pas plus grand que le triangle AHL. Mais il a aussî été démontré qu'il n'est pas plus petit. Il lui est donc nécessairement égal. C. Q. F. D.
Il faut savoir en outre que tout ce qui a été démontré jusqu'à présent, s'applique aux corps graves descendant ou montant le long de plans inclinés tout aussi bien qu'à ceux qui se meuvent suivant la verticale, puisque ce que nous avons posé touchant l'effet de la pesanteur doit être admis par même raison dans les deux casGa naar voetnoot1). Or de là il ne sera pas difficile de prouver la proposition suivante laquelle Galilée demandait qu'on lui accordât comme en quelque sorte évidente par elle-même. Car la démonstration qu'il a tâché d'en donner plus tard et qui se trouve dans l'édition postérieureGa naar voetnoot2) de ses ouvrages est peu solide, du moins à mon avis. Cette proposition est la suivante. | |||||||||||||||||||||||||||||||
Proposition VI.Les vitesses des corps pesants, acquises en descendant par des plans diversement inclinés, sont égales lorsque les élévations des plans le sont.
Nous appelons élévation d'un plan sa hauteur verticale. | |||||||||||||||||||||||||||||||
[pagina 141]
| |||||||||||||||||||||||||||||||
adjacentia, peragentur. Quare totum spatium motu accelerato peractum majus eritGa naar margenoot+ ipsa figura inscripta. Spatium vero illud aequale positum fuit plano P. Itaque figura inscripta minor erit spatio P. quod est absurdum; eodem enim spatio major ostensa fuit. Non est igitur planum P minus triangulo AHL. At neque majus esse ostendetur. Sit enim, si potest; & dividatur AH in partes aequales, atque ad earum altitudinem, inscripta circumscriptaque rursus, | ut ante, sit triangulo AHL figura ex rectangulis,Ga naar margenoot+ ita ut altera alteram excedat minori excessu quam quo planum P superat triangulum AHL, erit igitur necessario figura circumscripta minor plano P. Constat jam, prima temporis parte AC, minus spatium à mobili transmitti quam sit BC, quia hoc percurreretur eodem tempore AC cum celeritate aequabili CK, quam demum in fine temporis AC mobile adeptum est. Similiter secunda parte temporis CE, minus spatium motu accelerato transmittetur quam sit DE, quia hoc percurreretur eodem tempore CE, cum celeritate aequabili EO, quam demum in fine temporis CE mobile assequitur. Atque ita deinceps, singulis partibus temporis AH, minora spatia à mobili trajicientur quam sunt rectangula figurae circumscriptae, ipsis partibus adjacentia. Quare totum spatium motu accelerato peractum, minus erit ipsa figura circumscripta. Spatium vero illud aequale positum fuit plano P; ergo planum P minus quoque erit figura circumscripta. quod est absurdum, cum figura haec plano P minor ostensa fuerit. Ergo planum P non majus est triangulo AHL, sed nec minus esse jam ostenfum fuit. Ergo aequale sit necesse est; quod erat demonstrandum.
Et haec quidem omnia quae hactenus demonstrata sunt, gravibus per plana inclinata descendentibus atque ascendentibus aeque ac perpendiculariter motis convenire sciendum est: cum, quae de effectu gravitatis posita fuerunt, eadem ratione utrobique sint admittendaGa naar voetnoot1). Hinc vero non difficile jam erit demonstrare propositionem sequentem quam concedi sibi, ut quodammodo per se manifestam, Galileus postulavit. nam demonstratio illa quam postea adferre conatus est, quaeque in posteriori operum ejus editioneGa naar voetnoot2) extat, parum firma meo quidem judicio videtur. Est autem propositio hujusmodi. | |||||||||||||||||||||||||||||||
[pagina 142]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Considérons donc des plans inclinés dont AB et CB [Fig. 27] soient les sections faites par un plan vertical et dont les élévations AE et CD soient égales. Supposons
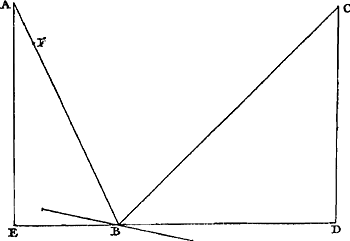 que le corps descende en tombant de A le long du plan AB et une autre fois de C le long du plan CB. Je dis que dans l'un et l'autre cas ce corps acquerra le même degré de vitesse au point B.
que le corps descende en tombant de A le long du plan AB et une autre fois de C le long du plan CB. Je dis que dans l'un et l'autre cas ce corps acquerra le même degré de vitesse au point B.
En effet si l'on dit que le corps tombant le long de CB acquiert une vitesse moindre qu'en tombant le long de AB, qu'il ait donc, après être tombé suivant CB, la vitesse qu'il pourrait acquérir aussi par une chute suivant FB, par hypothèse inférieure à AB. Mais en tombant suivant CB il acquerra une vitesse par laquelle il pourrait de nouveau remonter tout le long de BCGa naar margenoot*. Par conséquent il acquerra aussi en tombant selon FB la vitesse qui lui permetrait de remonter tout le long de BC. Si après être tombé de F en B il continue son mouvement par BC, ce qui peut être obtenu par réflexion sur une surface oblique, il s'élèvera donc jusqu'en C, c.à.d. à une hauteur supérieure à celle dont il était descendu, ce qui est absurde. On démontrera de la même manière qu'en tombant le long du plan AB il ne peut pas non plus acquérir une vitesse moindre que celle provenant de la chute le long de CB. Par conséquent la vitesse acquise par la chute suivant l'un ou l'autre plan est la même. C. Q. F. D.
Que si, au lieu de l'un ou de l'autre plan, on prend la verticale elle-même qui correspond à l'élévation des plans et qu'on fait tomber le mobile suivant cette verticale, il est certain que de cette façon aussi la même vitesse est obtenue que par la chute suivant les plans inclinés; en effet, la démonstration est la même. En nous basant là-dessus, nous pourrons maintenant donner auffi une bonne démonstration d'un deuxième théorème de Galilée sur lequel est bâtie toute la théorie qu'il a enseignée sur les plans inclinés. Savoir la | |||||||||||||||||||||||||||||||
Proposition VII.Les temps de chute le long de plans diversement inclinés, mais dont l'élévation est la même, sont entre eux comme les longueurs de ces plansGa naar voetnoot1). | |||||||||||||||||||||||||||||||
[pagina 143]
| |||||||||||||||||||||||||||||||
Sunto itaque plana inclinata, quorum sectiones factae plano ad horizontem erecto, AB, CB [Fig. 27], quorumque elevationes AE, CD | sint aequales; & cadat grave exGa naar margenoot+ A per planum AB, & rursus ex C per planum CB. dico utroque casu eundem gradumGa naar margenoot+ velocitatis in puncto B acquisiturum. Si enim per CB cadens minorem velocitatem acquirere dicatur quam cadens per AB, habeat ergo, per CB cadens, eam duntaxat quam per FB acquireret, posita nimirum FB minore quam AB. Acquiret autem per CB cadens eam velocitatem qua rursus per totam BC possit ascendereGa naar margenoot*. Ergo & per FB acquiret eam velocitatem qua possit ascendere per totam BC. Ideoque cadens ex F in B, si continuet porro motum per BC; quod repercussu ad superficiem obliquam fieri potest; ascendet usque in C, hoc est, altius quam unde decidit, quod est absurdum. Eodem modo ostendetur neque per planum AB decidenti minorem velocitatem acquiri quam per CB. Ergo per utraque plana eadem velocitas acquiritur, quod erat demonstrandum.
Quod si vero, pro plano alterutro, sumatur perpendiculum ipsum planorum elevationi aequale, per quod decidere mobile ponatur, sic quoque eandem quam per plana inclinata velocitatem ei acquiri constat; eadem namque est demonstratio. Porro hinc jam recte quoque procedet demonstratio alterius theorematis Galileani, cui reliqua omnia, quae de descensu super planis inclinatis tradidit, superstruuntur. Nempe | |||||||||||||||||||||||||||||||
Propositio VII.Tempora descensuum super planis diversimode inclinatis, sed quorum eadem est elevatio, esse inter se ut planorum longitudinesGa naar voetnoot1). | |||||||||||||||||||||||||||||||
[pagina 144]
| |||||||||||||||||||||||||||||||
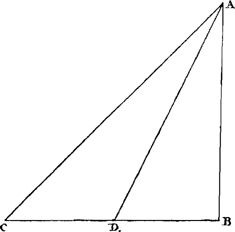 [Fig. 28.]Ga naar margenoot+
Soient AC et AD les plans inclinés de même élévation AB [Fig. 28]. Je dis que le temps de la descente le long du plan AC est à celui correspondant à AD comme la longueur AC est à AD. En effet, le temps d'une chute par AC est égal au temps d'un mouvement uniforme le long de AC avec la moitié de la vitesse acquise par la chute suivant ACGa naar margenoot*. De la même manière le temps correspondant à AD est égal à celui d'un mouvement uniforme suivant AD avec la moitié de la vitesse acquise par la chute suivant AD. Or, cette demi-vitesse est égale à l'autreGa naar margenoot*: par conséquent le temps rapporté du mouvement uniforme suivant AC sera au temps du mouvement uniforme suivant AD comme AC est à AD. Par conséquent les temps respectivement égaux à ceux-là, savoir le temps de chute le long de AC et celui le long de AD, auront entre eux le même rapport AC : AD. C. Q. F. D. On démontrera de la même manière que le temps de la descente suivant AC est au temps de la chute verticale le long de AB, comme sont entre elles les longueurs AC et AB. | |||||||||||||||||||||||||||||||
Proposition VIII.Lorsqu'un mobile descend d'un mouvement continu d'une hauteur déterminée par un nombre quelconque de plans contigus d'inclinaison quelconque, il finira toujours par acquérir la même vitesse, laquelle sera égale à celle qu'il acquerrait par une chute verticale de même hauteurGa naar voetnoot1).
Soient AB, BC, et CD [Fig. 29] les plans contigus, dont l'extrémité A ait audessus de la ligne horizontale DF, tracée par l'extrémité inférieure D, une hauteur égale à la perpendiculaire EF. Puisse le mobile descendre le long de ces plans de A jusqu'en D. Je dis qu'il aura en D la vitesse qu'il aurait en F s'il était tombé de E. En effet, supposons que le prolongement de CB coupe la droite AE en G, et celui de DC la même AE en E. Puisque le mobile en descendant suivant AB acquiert la même vitesse à l'extrémité B que lorsqu'il descend suivant GBGa naar margenoot*, il est manifeste, vu que par hypothèse le changement de direction au point B ne modifie nullement le mouvement, qu'il aura en parvenant au point C la même vitesse que s'il était descendu le long du plan GC, en d'autres termes que s'il était descendu suivant EC. Il parcourra donc aussi le dernier plan CD de la même manière que s'il était venu suivant EC, et il aura par conséquent au point extrême D une même vitesse que s'il était | |||||||||||||||||||||||||||||||
[pagina 145]
| |||||||||||||||||||||||||||||||
Sint plana inclinata AC, AD quorum eadem elevatio AB [Fig. 28]. dico | tempusGa naar margenoot+ descensus per planum AC ad tempus descensus per AD esse ut longitudo AC ad AD.Ga naar margenoot+ Est enim tempus per AC aequale tempori motus aequabilis per eandem AC, cum celeritate dimidia ejus quae acquiritur casu per ACGa naar margenoot*. Similiter tempus per AD est aequale tempori motus aequabilis per ipsam AD, cum dimidia celeritate ejus quae acquiritur casu per AD. Est autem haec dimidia celeritas illi dimidiae celeritati aequalisGa naar margenoot*, ideoque dictum tempus motus aequabilis per AC, ad tempus motus aequabilis per AD, erit ut AC ad AD. Ergo & tempora singulis istis aequalia, nimirum tempus descensus per AC, ad tempus descensus per AD, eandem rationem habebunt, nempe quam AC ad AD. quod erat demonstrandum. Eodem modo ostendetur & tempus descensus per AC, ad tempus casus per AB perpendicularem, esse ut AC ad AB longitudine. | |||||||||||||||||||||||||||||||
Propositio VIII.Si ex altitudine eadem descendat mobile continuato motu per quotlibet ac quaelibet plana contigua, utcunque inclinata; semper eandem in fine velocitatem acquiret, quae nimirum aequalis erit ei quam acquireret cadendo perpendiculariter ex pari altitudineGa naar voetnoot1). 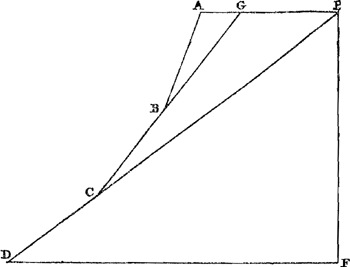 [Fig. 29.]
Sint plana contigua AB, BC, CD [Fig. 29], quorum terminus A, supra horizontalem lineam DF per infimum terminum D ductam, altitudinem habeat quanta est perpendicularis EF. descendatque mobile per plana illa ab A usque in D. Dico in D eam velocitatem habiturum quam, ex E cadens, haberet in F. Pro ducta enim CB occurrat rectae AE in G. Itemque DC producta | occurrat eidem AEGa naar margenoot+ in E. Quoniam itaque per AB descendens eandem acquirit velocitatem in termino B, atque descendens per GBGa naar margenoot*; manifestum est, cum flexus ad B nihil obstare motui ponatur, tantam velocitatem habiturum ubi in C pervenerit, quantam si per GC planum descendisset; hoc est, quantam haberet ex descensu per EC. Quare & reliquum planum CD eodem modo transibit ac si per EC advenisset, ac proinde in D denique parem velocitatem habebit, ac si descendisset per planum ED, | |||||||||||||||||||||||||||||||
[pagina 146]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ descendu suivant le plan ED, c.à.d. celle qui proviendrait aussi de la chute verticale selon EF. C. Q. F. D. Par là il appert aussi que si le mobile descend le long d'une circonférence de cercle ou bien d'une ligne courbe quelconque (car il est ici permis de confidérer les courbes comme composées d'une infinité de lignes droites) il acquiert toujours la même vitesse en descendant d'une même hauteur, savoir la vitesse qui résulterait d'une chute verticale. | |||||||||||||||||||||||||||||||
Proposition IX.Lorsqu'un corps grave, après être tombé, tourne son mouvement vers le haut, il atteindra la hauteur même dont il est venu, quel que soit le nombre des surfaces planes contigues et quelles que soient leurs inclinaisonsGa naar voetnoot1).
Puisse le corps tomber de la hauteur AB [Fig. 30]. Soient DC, CD et DE les plans inclinés. B représente le point le plus bas, l'autre extrémité E est située à la même hauteur que le point A. Je dis que si le mobile, après la chute le long de AB, change la direction de son mouvement de sorte qu'il le continue suivant les dits plans inclinés, il parviendra jusqu'en E. Qu'on dise en effet, si la chose est possible, qu'il n'arrive qu'en G. Prolongeons BC et CD jusqu'à leur rencontre en F et en H avec l'horizontale GF. Comme le mobile, après avoir parcouru les plans BC et CD, possède seulement la vitesse nécessaire pour escalader DG ou DH (car il est établi par la Prop. VI qu'il lui faut la même vitesse dans les deux cas), il avait donc, après avoir parcouru le plan BC, la vitesse nécessaire pour monter suivant CH ou CF. Il avait par conséquent en B la vitesse nécessaire pour monter le long de BF, c.à.d. celle qu'il pourrait acquérir en descendant le long de FB. Mais il possède en B une vitesse suffisante pour remonter jusqu'en A. Le corps pourrait donc avec la vitesse qu'il acquiert en descendant le long de FB remonter par BA, c.à.d. plus haut que son point de départ, ce qui est impossible. La démonstration est absolument la même quel que soit le nombre des plans suivant lesquels le mobile doive monter. Partant, lors même que le nombre des plans est infini, c.à.d. lorsqu'on a affaire à une courbe, le mobile s'élèvera par celle-ci aussi jusqu'à la hauteur dont il était descendu. | |||||||||||||||||||||||||||||||
[pagina 147]
| |||||||||||||||||||||||||||||||
hoc est, eandem quam ex casu perpendiculari per EF. quod erat demonstrandum.Ga naar margenoot+ Hinc liquet etiam per circuli circumferentiam, vel per curvam quamlibet lineam descendente mobili (nam curvas tanquam ex infinitis rectis compositae essent hic considerare licet) semper eandem illi velocitatem acquiri si ab aequali altitudine descenderit: tantamque eam esse velocitatem, quantam casu perpendiculari ex eadem altitudine adipisceretur. | |||||||||||||||||||||||||||||||
Propositio IX.Si grave, à descensu, sursum convertat motum suum, ascendet ad eandem unde venit altitudinem, per quascunque planas superficies contiguas, & quomodocunque inclinatas, incesseritGa naar voetnoot1). 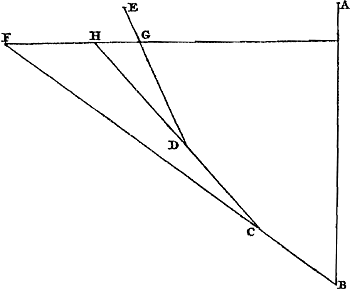 [Fig. 30.]
Cadat grave ex altitudine AB [Fig. 30], & ex puncto B inclinata sint sursum plana BC, CD, DE, quorum extremitas E sit eadem altitudine cum puncto A. Dico si mobile, post casum per AB, convertat motum ut pergat moveri per dicta plana inclinata, perventurum usque in E. Dicatur enim, sifieri potest,Ga naar margenoot+ tantum ad G perventurum. Producantur BC & CD, donec occurrant horizontali GF in F & H. Cum igitur mobile, superatis planis BC, CD, habeat tantum eam velocitatem quâ possit ascendere per DG, vel per DH; nam ad haec utraque eadem velocitate opus esse constat ex propositione 6; Ergo, superato plano BC, eam duntaxat habebat qua potuisset ascendere per CH, vel per CF. Ergo in B duntaxat eam qua potuisset ascendere per BF, hoc est, eandem quam acquireret descendendo per FB. Atqui in B habet velocitatem qua potest ascendere usque in A. Ergo illa velocitate quam acquirit grave descendendo per FB, posset ascendere per BA, hoc est, altius quam unde discesserat, quod fieri non potest. Est autem eadem prorsus demonstratio quotcunque plana fuerint per quae mobile ascendat. Unde & si infinita fuerit planorum multitudo, hoc est, si superficies aliqua curva ponatur, per hanc quoque ad eam ex qua venit altitudinem mobile assurget. | |||||||||||||||||||||||||||||||
[pagina 148]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Proposition X.Lorsqu'un mobile tombe perpendiculairement ou suivant une surface quelconque et qu'il est de nouveau porté en haut par la vitesse acquise suivant une autre surface quelconque, il aura toujours en montant et en descendant la même vitesse en des points situés à la même hauteurGa naar voetnoot1). 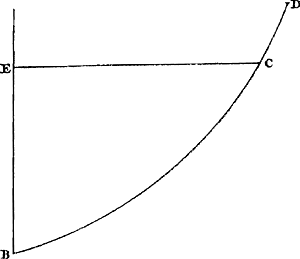 [Fig. 31.]
Considérons par exemple le cas où un mobile qui tombe de la hauteur AB [Fig. 31] continue ensuite son mouvement par la surface BCD dont le point C soit à la même hauteur que le point E situé sur la droite AB. Je dis que le mobile a en C la même vitesse qu'auparavant en E. En effet, comme il lui reste en C la vitesse nécessaire pour s'éleverjusqu'au point D situé à la même hauteur que AGa naar margenoot*, et comme il acquiert en tombant le long de AE la vitesse qui lui permettrait de s'élever, après invertissement du mouvement, suivant CDGa naar margenoot*, il apparaît que lorsqu'en montant il a attteint C il possède la même vitesse qu'il avait en E en descendant. C. Q. F. D. | |||||||||||||||||||||||||||||||
Proposition XI.Lorsqu'un mobile tend à descendre par quelque surface et qu'après l'invertissement du mouvement il est porté en haut par la même surface ou par une autre semblable et semblablement posée, il montera et descendra par le même espace en des temps égauxGa naar voetnoot2).
Considérons par exemple le cas où le mobile descend par la surface AB [Fig. 32] et remonte, après être parvenu en B (le mouvement étant interverti) le long de la même surface AB ou bien le long de la surface BC semblable et semblablement placée par rapport au plan de l'horizon; il apparaît par les démonstrations antérieures qu'il atteindra de nouveau la hauteur dont il est descendu. Or, comme il a partout aux points de même hauteur la même vitesse tant en montant qu'en descendantGa naar margenoot*, il est clair que la même ligne est parcourue deux fois avec des vitesses partout égales dans les deux cas, d'où résulte aussi que les temps des deux mouvements doivent être égaux. C. Q. F. D. | |||||||||||||||||||||||||||||||
[pagina 149]
| |||||||||||||||||||||||||||||||
Propositio X.Ga naar margenoot+Si mobile cadat perpendiculariter, vel per quamlibet superficiem descendat, ac rursus impetu concepto per quamlibet aliam feratur sursum, habebit ascendendo ac descendendo in punctis aeque altis eandem semper velocitatemGa naar voetnoot1).
Ut si mobile ex altitudine AB [Fig. 31] decidens, motum deinde continuet per superficiem BCD, in qua punctum C sit pari altitudine atque in AB est punctum E. Dico in C eandem velocitatem inesse mobili atque in E fuerat. Quum enim in C ea velocitas supersit mobili qua porro ascendat usque ad D punctum,Ga naar margenoot+ aeque altum ac AGa naar margenoot*: cumque & ex descensu per AE velocitatem eam acquirat qua, converso motu, ascensurum sit per CDGa naar margenoot*; Patet cum pervenit ad C ascendendo, eandem ipsum habere velocitatem, quam habebat in E descendendo; quod erat demonstrandum. | |||||||||||||||||||||||||||||||
Propositio XI.Si mobile per superficiem aliquam deorsum tendat, ac deinde converso motu sursum per eandem superficiem vel aliam similem similiterque positam feratur, aequalibus temporibus per idem spatium descendet atque ascendetGa naar voetnoot2). 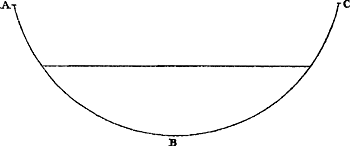 [Fig. 32.]
Velut si per superficiem AB descendat mobile [Fig. 32], atque ubi ad B pervenerit, converso motu sursum per eandem AB, vel ei similem & respectu plani horizontalis similiter positam BC, ascendat, constat ex ante demonstratis, perventurum ad eandem ex qua venit altitudinem. Cum autem perpetuo, in punctis quorum eadem altitudo, eandem velocitatem habeat ascendendo ac descendendoGa naar margenoot*; apparet eandem lineam bis eadem velocitate singulis sui partibus percurri: unde & tempora utriusque motus aequalia esse necesse est; quod erat demonstrandum. | |||||||||||||||||||||||||||||||
[pagina 150]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Proposition XIIGa naar voetnoot1).Considérons un cercle ABC [Fig. 33] de diamètre AC, auquel la droite FG est perpendiculaire. Supposons que cette dernière soit coupée en dehors du cercle par AF émanant de l'extrémité A du diamètre et coupant nécessairement la circonférence, par exemple en B. Je dis que l'arc BD, intercepté par les lignes GF et AF, est inférieur à la droite DF. 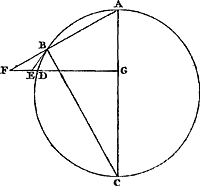 [Fig. 33.]
Joignons en effet les points B et C par une droite et tirons du point B une tangente BE à la circonférence, laquelle rencontrera nécessairement la droite FG entre F et D. L'angle BAC intérieur au cercle est donc égal à l'angle EBCGa naar voetnoot2). Par conséquent aussi l'angle FBE qui forme avec EBC l'angle droit FBC sera égal à BCA. Or, comme les triangles ABC et AGF sont semblables, l'angle F lui aussi sera égal à l'angle ACB. Le même angle F est donc égal à l'angle FBE. Par conséquent le triangle FEB est isoscèle, ayant les côtés égaux FE et EB. En ajoutant à chacun d'eux la droite ED, on aura donc l'égalité 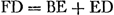 . Or, il est certain que l'ensemble de ces deux dernières droites est plus grand que l'arc BD ayant les mêmes extrémités et concave dans le même sens. Par conséquent FD sera aussi plus grand que le même arc BD. La proposition est donc démontrée. . Or, il est certain que l'ensemble de ces deux dernières droites est plus grand que l'arc BD ayant les mêmes extrémités et concave dans le même sens. Par conséquent FD sera aussi plus grand que le même arc BD. La proposition est donc démontrée.
| |||||||||||||||||||||||||||||||
Proposition XIIIGa naar voetnoot1).Si, dans les mêmes hypothèses, la droite AB coupe DG à l'intérieur du cercle [Fig. 34], je dis que l'arc BD, intercepté entre les droites GD et AB, est plus grand que la droite DF.
En effet, joignons par une droite les points D et C et traçons la corde correspondant à l'arc DB. Comme l'angle ABD est alors égal à ACD, c.à.d. à l'angle ADG, et que l'angle DFB est plus grand que l'angle ADF ou ADG, le même angle DFB sera plus grand que DBF. Par conséquent dans le triangle DFB le côté DB est plus grand que le côté DF. A-fortiori l'arc DB sera plus grand que la même droite DF. La proposition est donc démontrée. | |||||||||||||||||||||||||||||||
[pagina 151]
| |||||||||||||||||||||||||||||||
Propositio XIIGa naar voetnoot1).Ga naar margenoot+Esto circulus ABC [Fig. 33], diametro AC, cui ad angulos rectos sit FG; huicGa naar margenoot+ vero occurrat à termino diametri A educta AF extra circulum, quae quidem necessario secabit circumferentiam, puta in B. Dico arcum BD, lineis GF, AF interceptum, minorem esse recta DF.
Jungatur enim BC, & ducatur ex B puncto tangens circumferentiam recta BE, quae necessario occurret rectae FG inter F & D. Est igitur angulus BAC in circulo aequalis angulo EBCGa naar margenoot*. quare & angulus FBE, qui una cum EBC constituit angulum rectum FBC, erit aequalis BCA. Quia autem similia sunt triangula ABC, AGF, erit & angulus F aequalis angulo ACB. Ergo idem angulus F aequalis angulo FBE. Itaque isosceles est triangulus FEB, habens crura aequalia FE, EB. Addita ergo utrique eorum recta ED, fiet FD, aequalis duabus BE, ED. Hasce vero duas majores esse constat arcu BD, iisdem terminis intercepto, & in eandem partem cavo. Ergo & FD eodem arcu BD major erit: quare constat propositum. | |||||||||||||||||||||||||||||||
Propositio XIIIGa naar voetnoot1).Iisdem positis, si recta AB occurrat ipsi DG intra circulum [Fig. 34]; Dico arcum BD, rectis GD, AB interceptum, majorem esse recta DF. 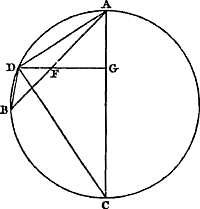 [Fig. 34.]
Jungatur enim DC & ducatur arcui DB subtensa DB. Quoniam ergo angulus ABD aequalis ACD, hoc est, angulo ADG; angulus autem DFB major angulo ADF, sive ADG; erit | idem DFB etiamGa naar margenoot+ major DBF. Ergo in triangulo DFB latus DB majus latere DF; unde multo magis arcus DB superabit eandem DF. Quare constat propositum. | |||||||||||||||||||||||||||||||
[pagina 152]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Proposition XIV.Soit ABC une cycloïde [Fig. 35], AC sa base, BD son axe. Je pense qu'on voit avec évidence comment cette ligne est engendrée suivant ce qui a été exposé plus haut sur sa définition et sa description mécaniqueGa naar voetnoot1). Soit de plus BGD un cercle symétrique par rapport à l'axe BD. Traçons EF parallèlement à la base AC par un point E arbitrairement choisi sur la cycloïde, laquelle parallèle coupe l'axe BD en F et la circonférence BGD en G. Je dis que la droite GE est égale à l'arc GBGa naar voetnoot2)  [Fig. 35.]
En effet, soit décrite par le point E une circonférence de cercle LEK égale à BGD et touchant la base de la cycloïde en K. Menons aussi le diamètre KL. La droite AK est donc égale à l'arc EK. Mais la longueur entière AD est égale à la demi-circonférence KEL; par conséquent KD est égale à l'arc EL ou GB. Or, KD ou NF est égale à EG, puisque EN = GF et que la partie NG leur est commune. Il est donc prouvé qu'on a aussi: GE = arc GB. | |||||||||||||||||||||||||||||||
Proposition XV.Un point sur une cycloïde étant donné, mener par lui une tangente à la cycloïdeGa naar voetnoot3).
Soit ABC [Fig. 36] la cycloïde et B le point donné sur lui par lequel il faut mener la tangente. Construisons autour de l'axe AD de la cycloïde le cercle générateur AED et menons BE parallèlement à la base de la cycloïde, laquelle parallèle coupe la circonférence du cercle nommé en E. Joignons les points A et E par une droite et tirons enfin par B une parallèle HBN à cette dernière. Je dis que cette parallèle touche la cycloïde en B. En effet, prenons sur la parallèle un point H quelconque différent de B, d'abord | |||||||||||||||||||||||||||||||
[pagina 153]
| |||||||||||||||||||||||||||||||
Propositio XIV.Ga naar margenoot+Sit cyclois ABC [Fig. 35] cujus basis AC axis BD. Quomodo autem generetur ex definitione & descriptione mechanica superuis traditis satis manifestum arbitrorGa naar voetnoot1). Et circa axem BD, circulus descriptus st BGD, & à quolibet puncto E in cycloide sumpto agatur EF basi AC parallela, quae occurrat axi BD in F, secetque circumferentiam BGD in G, Dico rectam GE arcui GB aequalem esseGa naar voetnoot2).
Describatur enim per E punctum circulus LEK ipsi BGD aequalis, quique tangat basin cycloidis in K, & ducatur diameter KL. Est igitur recta AK arcui EK aequalis; sed tota AD aequalis semicircumferentiae KEL; ergo KD aequalis arcui EL sive GB. Est autem KD sive NF aequalis EG, quoniam EN aequalis GF, & communis utrique NG. Ergo constat & GE aequalem esse arcui GB. | |||||||||||||||||||||||||||||||
Propositio XV.Ga naar margenoot+Dato in Cycloide puncto, rectam per illud ducere quae Cycloidem tangatGa naar voetnoot3).  [Fig. 36.]
Sit cyclois ABC [Fig. 36], & punctum in ea datum B, per quod tangentem ducere oporteat. Circa axem cycloidis AD describatur circulus genitor AED, & ducatur BE parallela basi cycloidis, quae dicto circulo occurrat in E, & jungatur AE, cui denique parallela per B agatur HBN. Dico hanc cycloidem in B contingere. Sumatur enim in ea punctum quodlibet, à B diversum, ac primo versus superiora | |||||||||||||||||||||||||||||||
[pagina 154]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ vers le haut, et menons par H une droite parallèle à la base de la cycloïde, coupant celle-ci en L, la circonférence AED en K et la droite AE en M. Comme KL est alors égale à l'arc KA et que la droite KM est plus petite que l'arc KE, la droite ML sera inférieure à l'arc AE, c.à.d. à la droite EB ou MH; d'où il apparaît que le point H est situé en dehors de la cycloïde. Prenons en second lieu sur la droite HN un point N situé au-dessous de B et menons, comme plus haut, par N une droite parallèle à la base, coupant la cycloïde en Q, la circonférence AED en O, et le prolongement de la droite AE en P. Comme OQ est alors égale à l'arc OA et que OP est plus grande que l'arc OE, PQ sera inférieure à l'arc EA, c.à.d. à la droite EB ou PN. D'où il apparaît de nouveau que le point N se trouve en dehors de la cycloïde. Puisque tous les points pris sur la droite HBN, excepté B, sont donc situés en dehors de la cycloïde, il est établi que cette droite touche la cycloïde en B. C. Q. F. D. J'ai douté si je laisserais cette place à cette démonstration, puisque je trouve qu'une preuve presque semblable de Mons. Wren a été publiée dans le livre de Wallis sur la CycloïdeGa naar voetnoot1). Mais on peut également appliquer à cette proposition une méthode générale qui ne convient pas seulement cycloïde mais aussi aux autre lignes courbes engendrées par la rotation d'une figure quelconque, pourvu que cc soit une figure ayant sa concavité d'un même côté et qui appartienne au genre des courbes dites géométriques. En effet, considérons une courbe NAB [Fig. 37]Ga naar voetnoot2) provenant de la rotation de la figure OL sur la règle LD, c.à.d. une courbe décrite par le point N pris sur le contour de la figure OL, et qu'il s'agisse de mener une tangente en A qui est un point de la courbe. Menons une droite CA du point C où la figure touchait la règle lorsque le point qui décrit la figure était en A. Ce point de contact peut toujours être trouvé, puisque le problème se réduit à tirer deux lignes parallèles entre elles dont l'une passe par le point donné du contour qui décrit la figure tandis que l'autre touche la figure, la distance des deux parallèles étant égale à celle du point donné A à la règle LD. Je dis que CA rencontre la courbe à angles droits, en d'autres termes que la circonférence de cercle MAF décrite du centre C avec le rayon CA touche la courbe au point A, de sorte qu'une droite perpendiculaire à AC et passant par le point A touchera la courbe en ce point. | |||||||||||||||||||||||||||||||
[pagina 155]
| |||||||||||||||||||||||||||||||
velut H, & per H ducatur recta basi cycloidis parallela, quae occurrat cycloidi in L,Ga naar margenoot+ circulo AED in K, rectae AE in M. Quia ergo KL est aequalis arcui KA, recta autem KM minor arcu KE, erit recta ML minor arcu AE, hoc est, rectâ EB, sive MH; unde apparet punctum H esse extra cycloidem. Deinde in recta HN sumatur punctum N inferius B, & per N agatur, ut ante, basi parallela, quae occurrat cycloidi in Q, circulo AED in O, rectae AE productae in P. Quia ergo OQ, aequalis est arcui OA; OP autem major arcu OE; erit PQ minor arcu EA, hoc est, rectâ EB, sive PN. Unde apparet rursus punctum N esse extra cycloidem. Cum igitur quodlibet punctum praeter B, in recta HBN sumptum, sit extra cycloidem, constat illam in puncto B cycloidem contingere; quod erat demonstrandum.
EA, hoc est, rectâ EB, sive PN. Unde apparet rursus punctum N esse extra cycloidem. Cum igitur quodlibet punctum praeter B, in recta HBN sumptum, sit extra cycloidem, constat illam in puncto B cycloidem contingere; quod erat demonstrandum.
Huic demonstrationi an locum suum hic relinquerem dubitavi, quod non multum ei absimilem à clarissimo Wrennio editam inveniam in libro Wallifii de Cycloide. Potest autem & universali constructione propositum absolviGa naar voetnoot1), quae non cycloide tantum sed & aliis curvis, ex cujuslibet figurae circumvolutione genitis, conveniat; dummodo fit figura in eandem partem cava, & ex iis quae geometricae vocantur. Sit enim curva NAB [Fig. 37]Ga naar voetnoot2), orta ex circumvolutione figurae OL super regulaGa naar margenoot+ LD; describente nempe puncto N, in circumferentia figurae OL sumpto. Et oporteat ad punctum curvae A tangentem ducere. Ducatur recta CA à puncto C, ubi figura regulam tangebat cum punctum describens esset in A: quod punctum contactus semper inveniri potest, siquidem eo reducitur problema ut duae rectae inter se parallelae ducendae sint, quarum altera transeat per punctum describens in figurae ambitu datum, altera figuram tangat, quaeque inter se distent quantum distat punctum datum A ab regula LD: dico ipsam CA occurrere curvae ad angulos rectos, sive circumferentiam MAF descriptam centro C radio CA, tangere curvam in puncto A, unde perpendicularis ad AC, per punctum A, ducta curvam ibidem continget. | |||||||||||||||||||||||||||||||
[pagina 156]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ En effet, tirons d'abord CB à un point B de la courbe plus distant de la règle LD que le point A, et considérons la position BED de la figure au moment où le point décrivant est en B, D étant alors le point de contact de la figure avec la règle. Supposons maintenant élevé jusqu'en E le point de la courbe qui était en C au moment où le point décrivant était en A. Menons les droites EC et EB et soit KH, coupant la règle en H, une tangente à la figure donnée en E. Comme la droite CD est alors égale à la courbe ED et que la somme des longueurs EH et HD est plus grande que cette courbe, EH sera plus grande que CH. D'où ∠ ECH > ∠ CEH et par conséquent ∠ ECL > ∠ CEK. Mais en ajoutant ∠ KEB égal à ∠ LCA à ∠ KEC, on obtient ∠ CEB; et en soustrayant de ∠ ECL l'angle LCB, on obtient ∠ ECB. L'angle CEB est donc certainement supérieur à l'angle ECB. Par conséquent dans le triangle CEB le côté CB sera plus grand que KB. Mais il est clair que EB = CA, puisque c'est la même longueur transportée avec la figure. Donc CB sera aussi plus grande que CA, c.à.d. que CF. D'où il appert que le point B est en dehors de la circonférence de cercle MAF. Considérons d'autre part un point N pris sur la courbe entre la règle LD et le point A, et supposons que lorsque le point décrivant la courbe était en N, la situation de la figure était en VL et le point de contact en L. Supposons en outre élevé jusqu'en V le point qui touchait d'abord la règle en C, et tirons les droites CN, NV, VC et VL. On aura donc VN = CA, car CA a été transportée en VN. Or, comme la droite LC est égale à la courbe LV et par conséquent plus grande que la droite LV, dans le triangle CLV l'angle LVC sera plus grand que l'angle LCV. C'est pourquoi, si l'on ajoute encore ∠ LVN à ∠ LVC, l'angle total NVC sera certainement plus grand que ∠ LCV et a-fortiori que ∠ NCV, qui est une partie de ∠ LCV. Par conséquent dans le triangle CVN le côté CN sera plus grand que le côté VN égal à CA; partant CN sera aussi plus grand que CA, c.à.d. que CM. D'où il ressort que le point N tombe en dehors du cercle MAF, lequel touchera donc la courbe au point A. C. Q. F. D. Or, la construction comme la démonstration sont les mêmes si la courbe est engendrée par un point décrivant se trouvant soit à l'intérieur soit à l'extérieur du contour de la figure roulante. Excepté que dans ce dernier cas une partie de la courbe descend sous la règle, d'où résulte une modification de la démonstration. En effet, soit donné le point A, par lequel la tangente doit être menée, sur une partie NAB de la courbe située au-dessous de la règle CL [Fig. 38]Ga naar voetnoot1) laquelle courbe est décrite par le point N pris en dehors de la figure roulante mais occupant une position bien déterminée dans son plan. Après avoir trouvé le point C où la figure roulante touche la règle CD lorsque le point décrivant est en A, menons la droite CA. Je dis que celle-ci rencontre la courbe NAB à angles droits, en d'autres termes que la circonférence décrite du centre C avec le rayon CA touche la courbe NAB au point A. Or, nous démontrerons qu'elle la touche extérieurement tandis que dans la partie de la courbe située au-dessus de la règle CD elle la touche intérieurement. En effet, toutes choses étant posées et décrites comme plus haut, nous démontrons | |||||||||||||||||||||||||||||||
[pagina 157]
| |||||||||||||||||||||||||||||||
Ducatur enim CB primum ad punctum curvae B, quod distet ultra punctum A abGa naar margenoot+ regula LD, intelligaturque figurae positus in BED, cum punctum describens esset in B, contactus regulae in D. & punctum curvae quod erat in C, cum punctum describens esset in A, hic jam sublatum sit in E; & jungantur EC, EB, tangatque figuram in E recta KH, occurrens regulae in H. Quia ergo recta CD aequalis est curvae ED; eâdem vero curva major est utraque simul EH, HD; erit EH major quam CH. Unde angulus ECH major quam CEH, & proinde ECL minor quam CEK. Atqui addendo angulum KEB, qui aequalis est LCA, ad KEC, fit angulus CEB: & auferendo ab ECL angulum LCB, fit ECB. Ergo angulus CEB major omnino angulo ECB. Itaque in triangulo CEB, latus CB majus erit quam EB. sed EB aequale patet esse CA, cum sit idemmet ipsum unà cum figura transposi|tum. Ergo CB etiam major quam CA, hoc est, quam CF. unde constatGa naar margenoot+ punctum B esse extra circumferentiam MAF. Sit rursus punctum N in curva sumptum inter regulam LD & punctum A. Cumque punctum describens esset in N, ponatur situs figurae fuisse in VL, punctumque contactus L, punctum verò quod tangebat prius regulam in C, sit jam sublatum in V: & jungantur CN, NV, VC, VL. Erit ergo VN aequalis CA; imo erit ipsa CA translata in VN. Jam quia recta LC aequatur curvae LV, ac proinde major est recta LV, erit in triangulo CLV angulus LVC major quam LCV. Quare addito insuper angulo LVN ad LVC, fiet totus NVC major utique quam LCV, ac proinde omnino major angulo NCV, qui pars est LCV. Ergo in triangulo CVN latus CN majus erit latere VN, cui aequatur CA, ideoque CN major quoque quam CA, hoc est quam CM. Unde apparet punctum N cadere extra circulum MAF, qui proinde tanget curvam in puncto A. quod erat demonstrandum. Est autem eadem quoque tum constructio tum demonstratio, si curva genita sit à puncto describente, vel intra vel extra ambitum figurae circumvolutae sumpto. Nisi quod, hoc posteriori casu, pars quaedam curvae infra regulam descendit, unde non-nulla in demonstratione oritur diversitas. Sit enim punctum A, per quod tangens ducenda est, datum in parte curvae NAB, quae infra regulam CL descendit [Fig. 38]Ga naar voetnoot1), descripta nimirum à puncto N extra figuram revolutam sumpto, sed certam | positionem in eodem ipsius plano habente. InventoGa naar margenoot+ igitur puncto C, ubi figura revoluta tangit regulam CD quum punctum describens esset in A, ducatur recta CA. Dico hanc curvae NAB occurrere ad rectos angulos, sive circumferentiam radio CA centro C descriptam tangere curvam NAB in puncto A. Ostendetur autem exterius ipsam contingere, cum in curvae parte supra regulam CD posita interius contingat. Positis enim & descriptis iisdem omnibus quae prius, ostenditur rursus angulus ECH | |||||||||||||||||||||||||||||||
[pagina 158]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ [Fig. 38.]
de nouveau que ∠ ECH > ∠ CEH. Mais si à ∠ ECH on ajoute ∠ HCB on obtient ∠ ECB, et en retranchant ∠ HEB égal à ∠ DCA de ∠ CEH, on obtient ∠ CEB. Par conséquent ∠ ECB est certainement supérieur à ∠ CEB. Par conséquent dans le triangle ECB le côté EB est plus grand que CB. Mais CA ou CF est égale à EB. Par conséquent on a aussi CF, CB; le point F de la circonférence de cercle est donc à l'extérieur de la courbe NAB par rapport au centre. On montre de nouveau comme précédemment que ∠ LVC > ∠ LCV. Par conséquent ∠ CVP, supplément de ∠ LVC, sera inférieur à ∠ VCD. Mais si l'on ajoute à ∠ VCD ∠ DCN, on obtient ∠ VCN; et si l'on retranche de ∠ CVP ∠ PVN, on obtient ∠ CVN. Par conséquent l'angle VCN est certainement plus grand que l'angle CVN. Dans le triangle CVN le côté VN sera donc plus grand que CN. Or, CA ou CM est égale à VN. Partant, CM aussi sera plus grande que CN; le point M de la circonférence de cercle sera donc à une telle distance du centre C qu'il se trouvera à l'extérieur de la courbe NAB. Il est donc établi que la circonférence MAF touche la courbe au point A. C. Q. F. D. Qui si le point de la courbe par lequel il faut mener la tangente est précisément celui où la règle coupe la courbe, la tangente cherchée sera toujours perpendiculaire à la règle, comme il serait facile de le démontrer. | |||||||||||||||||||||||||||||||
Proposition XVI.Ga naar margenoot+ Si deux droites parallèles AF et BG, dont l'une et l'autre est située du même côté du centre ou dont l'une AF passe par le centre lui-même, coupent une circonférence de cercle [Fig. 39], et qu'on mène en A, où la parallèle la plus proche du centre la coupe, une droite qui touche la circonférence, je dis que la partie AB de cette tangente qui est interceptée par les deux parallèles est inférieure à l'arc AC compris entre ces mêmes parallèles. | |||||||||||||||||||||||||||||||
[pagina 159]
| |||||||||||||||||||||||||||||||
major quam CEH. atqui ad ECH addito HCB fit angulus ECB; & à CEH auferendoGa naar margenoot+ HEB, qui aequalis est DCA, fit angulus CEB. Ergo ECB major omnino quam CEB. unde in triangulo ECB latus EB majus quam CB. sed ipsi EB aequalis est CA, sive CF. Ergo & CF major quam CB: ideoque punctum circumferentiae F est ultra curvam NAB à centro remotum. Item rursus ostenditur angulus LVC major LCV. Quare CVP, qui cum LVC duos rectos aequat, minor erit quam VCD. Atqui addendo ad VCD angulum DCN, fit VCN; & auferendo ab CVP angulum PVN, fit CVN. Ergo angulus VCN omnino major quam CVN. In triangulo itaque CVN, latus VN majus erit quam CN. Est autem ipsi VN aequalis CA sive CM. Ergo & CM major quam CN, ideoque punctum circumferentiae M erit ultra curvam NAB à centro C remotum. Itaque constat circumferentiam MAF tangere curvam in puncto A. quod erat demonstrandum. Quod si punctum curvae per quod tangens ducenda est, sit illud ipsum ubi regula curvam secat, erit tangens quaesita semper regulae perpendicularis; ut facile esset ostendere. | |||||||||||||||||||||||||||||||
Propositio XVI.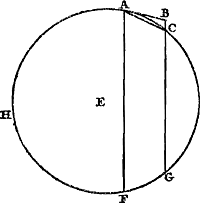 [Fig. 39.]
Si circuli circumferentiam, cujus centrum E,Ga naar margenoot+ secent rectae duae parallelae AF, BG, quarum utraque ad eandem partem centri transeat, vel altera AF per centrum ipsum [Fig. 39]: & à puncto A, quo centro propior circumferentiam secat, ducatur recta ipsam contingens: dico partem hujus AB, à parallela utraque interceptam, minorem esse arcu AC, ab utraque eadem parallela intercepto. | |||||||||||||||||||||||||||||||
[pagina 160]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ En effet, tirons la corde correspondant à l'arc AC. Comme l'angle BAF est alors égal à celui que comprend la portion du cercle AHF, laquelle est plus grande que le demi-cercle, à moins que ce ne soit le demi-cercle lui-même, l'angle BAF sera inférieur ou égal à un angle droit; par conséquent l'angle ABC est supérieur ou égal à un angle droit. Par conséquent dans le triangle ABC le côté AC opposé à l'angle B sera plus grand que le côté AB. Mais le même côté AC est inférieur à l'arc AC. Le côté AB lui aussi sera donc, a-fortiori, plus petit que l'arc AC. | |||||||||||||||||||||||||||||||
Proposition XVII.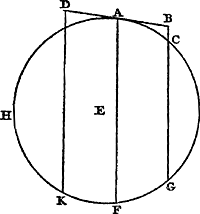 [Fig. 40.]
Les mêmes choses étant supposées, si une troisième droite DK [Fig. 40] parallèle aux précédentes coupe le cercle, parallèle dont la distance à AF qui est la plus proche du centre est égale à celle de AF à l'autre parallèle BG, je dis que la partie de la tangente en A interceptée par la troisième parallèle et la moyenne, savoir AD, est plus petite que l'arc AC compris entre les deux premières parallèles.
Ceci est évident puisque AD = AB, et que nous venons de démontrer que AB est plus petite que l'arc AC. | |||||||||||||||||||||||||||||||
Proposition XVIII.Lorsque deux droites parallèles AF et BG [Fig. 41] coupent un cercle à centre E et que l'on mène du point B où celle qui est la plus éloignée du centre (ou bien également éloignée du centre que l'autre) coupe la circonférence, une droite qui touche cette dernière, la partie BA de cette tangente, interceptée par les parallèles, sera plus grande que l'arc BC compris entre ces mêmes parallèles.
En effet, menons au point C la tangente MCL à la circonférence, et puisse-t-elle couper la tangente BA en L. Dans le triangle ACL, l'angle C est égal à l'angle MCF, c.à.d. à l'angle compris dans la portion de cercle CBF. D'autre part l'angle A est égal à celui qui comprend la portion BCG du cercle, et comme cette dernière est plus grande que la portion CBF ou bien son égale, attendu que BG est situé à plus grande, ou bien à égale, distance du centre que CF, l'angle A du triangle ACL sera plus petit que l'angle C ou bien égal à lui, et par conséquent le côté CL plus petit que l'angle AL ou bien son égal. Mais la somme de CL et de LB est plus grande que l'arc CB. Par conséquent la somme de AL et de LB, c.à.d. la tangente AB, sera aussi plus grande que le même arc CB. C. Q. F. D. | |||||||||||||||||||||||||||||||
[pagina 161]
| |||||||||||||||||||||||||||||||
Ducatur enim arcui AC subtensa recta AC. Quia ergo angulus BAF est aequalis eiGa naar margenoot+ quem capit portio circuli AHF, quae vel major est semicirculo vel semicirculus, erit proinde angulus BAF, | vel minor recto vel rectus; ideoque angulus ABC vel majorGa naar margenoot+ recto vel rectus. Quare in triangulo ABC latus AC, angulo B subtensum, majus erit latere AB. sed idem latus AC minus est arcu AC. Ergo omnino & AB arcu AC minor erit. | |||||||||||||||||||||||||||||||
Propositio XVII.Iisdem positis, si tertia recta prioribus parallela DK [Fig. 40], circulum secuerit, quae ab ea quae centro propior est AF, tantundem distet quantum haec à reliqua BG: dico partem tangentis in A, à parallela ultimo adjecta, & media interceptam, nempe AD, arcu AC à primis duabus parallelis intercepto minorem esse.
Hoc enim patet quum AD ipsi AB aequalis sit, quam antea ostendimus arcu AC minorem esse. | |||||||||||||||||||||||||||||||
Propositio XVIII.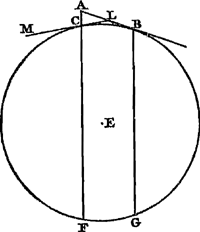 [Fig. 41.]
Si circulum, cujus centrum E, duae rectae parallelae secuerint AF, BG [Fig. 41]; & à puncto B, ubi quae à centro remotior est, vel tantundem atque altera distat, circumferentiae oc|currit, ducatur recta circumferentiamGa naar margenoot+ tangens: erit pars hujus BA, à parallelis intercepta, major arcu ab iisdem parallelis intercepto BC.
Ducatur enim in puncto C, recta MCL circumferentiam tangens, quae occurrat tangenti BA in L. In triangulo igitur ACL, angulus C aequalis est angulo MCF, hoc est, ei quem capit portio circuli CBF. angulus autem A aequatur angulo quem capit portio circuli BCG, quae portio quum sit major vel aequalis portioni CBF, quippe quum BG vel ulterius distet à centro quam CF, vel tantundem: erit proinde trianguli ACL angulus A minor vel aequalis angulo C: & consequenter latus CL vel minus vel aequale lateri AL. Atqui CL una cum LB majores sunt arcu CB. Ergo & AL una cum LB, hoc est, tangens AB, eodem arcu CB major erit. quod erat demonstrandum. | |||||||||||||||||||||||||||||||
[pagina 162]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Proposition XIX.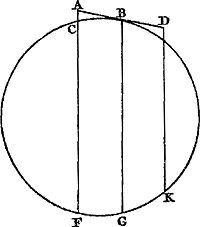 [Fig. 42.]
Les mêmes choses étant posées, si une troisième droite DK [Fig. 42] parallèle aux précédentes coupe la circonférence, parallèle dont la distance à celle qui est la plus éloignée du centre est égale à celle de cette dernière à celle qui reste, savoir AF, la partie de la tangente en B interceptée entre la parallèle moyenne et la troisième DK, c.à.d. BD, sera plus grande que l'arc BC.
Ceci est évident puisque BD est égale à BA, dont nous avons démontré qu'elle est plus grande que l'arc BC. | |||||||||||||||||||||||||||||||
Proposition XX.Lorsqu'un arc de cercle AB [Fig.43] inférieur à une demi-circonférence est coupé en un nombre quelconque de parties par des lignes droites parallèles, équidistantes tant entre elles qu'aux parallèles tirées par les extrémités de l'arc, telles que CD, EF, GH, KL etc. et qu'on mène à la première extrémité A de l'arc, ainsi qu'aux autres points de division, des tangentes à la circonférence, toutes vers le même côté, chacune jusqu'au point de rencontre avec la parallèle suivante, comme les tangentes AC, DE, FG, HK, etc., je dis que la somme de ces tangentes, diminuée de la première AC, est moindre que l'arc donné AB. Mais que ces tangentes, si l'on conserve AC, sont ensemble plus grandes que l'arc AB diminué de la partie extrême NB, en d'autres termes que l'arc AN.
En effet, supposons d'abord qu'il y ait des parallèles de part et d'autre du centre Z, et soit GH, parmi celles qui se trouvent du côté B, la plus proche du centre par lequel elle peut même passer. Par conséquent chacune des tangentes comprises entre GH et BO, telles que HK, LM et NO, est moindre que l'arc correspondantGa naar margenoot*. Mais de plus la tangente GF est inférieure à l'arc suivant FDGa naar margenoot* et pareillement la tangente ED à l'atc DA. La somme des tangentes comprises entre BO et CD est donc plus petite que celle des arcs BH et FA et a-fortiori que celle des arcs BH et HA, c.à.d. que l'arc BA. C. Q. F. D. Nous démontrerons maintenant que la somme des tangentes comprises entre BO et A est plus grande que l'arc AN. Car la parallèle GH passera plus près du centre Z que la parallèle EF que je suppose être la plus proche de celles qui se trouvent du côté A, ou bien elle en sera éloignée à plus grande distance, ou bien à la même distance. Que si EF est à plus grande, ou à égale, distance du centre que GH, la tangente | |||||||||||||||||||||||||||||||
[pagina 163]
| |||||||||||||||||||||||||||||||
Propositio XIX.Ga naar margenoot+Iisdem positis, si tertia recta prioribus parallela DK [Fig. 42] circulum secet, quae tantundem distet ab ea quae remotior est à centro quantum haec à reliqua AF: Erit pars tangentis in B, | à parallela media, & ultimo addita DK, intercepta,Ga naar margenoot+ nimirum BD, major arcu BC.
Hoc enim manifestum est cum BD fiat ipsi BA aequalis, quam ostendimus arcu BC majorem esse. | |||||||||||||||||||||||||||||||
Propositio XX.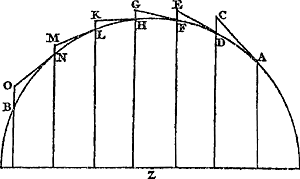 [Fig. 43.]
Si arcus circuli, semicircumferentia minor, AB [Fig. 43], in partes quotlibet secetur lineis rectis parallelis, quae & inter se, & cum rectis sibi parallelis per terminos arcus ductis, aequalia intervalla constituant, quales sunt CD, EF, GH, KL &c. ducanturque ad terminum arcus alterutrum A, & ad reliqua omnia sectionum puncta rectae circumferentiam tangentes, omnes in eandem partem, & ut unaquaeque occurrat proximae dictarum parallelarum; cujusmodi sunt tangentes AC, DE, FG, HK &c. Dico has tangentes, dempta prima AC, simul sumptas, minores esse arcu proposito AB. Easdem vero omnes, non omissa AC, majores esse arcu AB diminuto parte extrema NB, hoc est, majores arcu AN.
Ponamus enim primo parallelarum aliquas transire ab utraque parte centri Z, & sit GH, earum quae sunt à parte B, centro proxima, vel per ipsum centrum transeat. Itaque tangentes omnes inter GH & BO comprehensae, ut HK, LM, NO, singulae suis arcubus minores suntGa naar margenoot*. Porro autem & tangens GF, arcu sequente FD minor estGa naar margenoot*, & similiter tangens ED arcu DA. Itaque tangentes omnes inter BO & CD interjectae, minores sunt arcubus BH & FA, ac proinde omnino minores arcubus BH, HA, sive arcu BA, quod erat primo ostendendum. Porro jam demonstrabimus tangentes omnes inter BO & A majores esse arcu AN. Enimvero parallela GH, vel propius centrum Z transit quam parallela EF, quam pono proximam esse | earum quae à parte A transeunt, vel erit remotior, ve] aequeGa naar margenoot+ distabit. Quod si EF longius à centro vel aeque remota est ac GH, erit tangens FG major | |||||||||||||||||||||||||||||||
[pagina 164]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ FG sera supérieure à son arc FH, et chacune des autres tangentes situées du côté A, savoir ED et CA, surpassera l'arc correspondantGa naar margenoot*; de sorte que la somme totale GF + ED + CA sera plus grande que l'arc HA. Mais de plus la tangente LM sera plus grande que l'arc HLGa naar margenoot*, et la tangente NO que l'arc LN; par conséquent la somme des tangentes, avec l'exception de HK, sera plus grande que l'arc AN; à plus forte raison, lorsque HK aussi vient s'y ajouter, la somme des tangentes comprises entre A et B sera-t-elle plus grande que ce même arc AN. Mais si GH est plus éloignée du centre que EF, la tangente KH sera plus grande que l'arc HFGa naar margenoot*, la tangente ML comme ci-devant plus grande que l'arc LH, la tangente ON plus grande que l'arc NL, et par conséquent la somme des tangentes ON, ML et KH plus grande que l'arc NF. D'autre part la tangente ED sera plus grande que son arc FDGa naar margenoot* et de même la tangente CA que l'arc correspondant DA. Par conséquent la somme des tangentes comprises entre BO et A, excepté GF, sera plus grande que l'arc NA; et a-fortiori la somme des mêmes tangentes, GF comprise, c.à.d. celle de toutes les tangentes situées entre BO et A, surpassera le même arc NA. Par ces considérations la démonstration est encore manifeste dans les autres cas, quelqu'arc de la demi-circonférence qu'on prenne; elle est ou entièrement la même ou bien une partie seulement de la démonstration précédente. | |||||||||||||||||||||||||||||||
Proposition XXI.Lorsqu'un mobile descend d'un mouvement continu le long de certains plans inclinés contigus quelconques, et qu'une autre fois il descend de la même hauteur par un même nombre de plans contigus, ainsi construits que chacun d'eux correspond en hauteur à un des plans précédents, mais que le deuxième plan a toujours une plus grande inclinaison que le premier; je dis que le temps de la descente le long des plans moins inclinés est plus bref que celui de la descente par les plans plus inclinés.
Soient les deux séries de plans comprises entre les mêmes parallèles horizontales ABCDE et FGHKL [Fig. 44], et supposons que deux plans correspondants l'un de la première, l'autre de la deuxième série, soient toujours renfermés entre les mêmes parallèles horizontales; supposons en outre que chaque plan de la série FGHKLGa naar voetnoot1) soit plus incliné par rapport à l'horizon que le plan correspondant de même hauteur de la série ABCDE. Je dis que la chute le long de ABCDE se sera en un temps plus court que celle le long de FGHKL.
En effet, il est d'abord manifeste que le temps de la descente par AB est plus court que celui de la descente par FG, puisque le rapport de ces temps est égal à celui des droites AB et FGGa naar margenoot* et que AB <FG, à cause de son inclinaison moins forte. Prolon- | |||||||||||||||||||||||||||||||
[pagina 165]
| |||||||||||||||||||||||||||||||
arcu suo FH, & reliquae tangentes versus A, nimirum ED, CA majores singulae arcubusGa naar margenoot+ suisGa naar margenoot*; adeo ut omnes simul GF, ED, CA majores sint arcu HA. sed & arcu HL major erit tangens LMGa naar margenoot*, & arcu LN tangens NO, itaque tangentes omnes, praeter HK, majores simul erunt arcu AN; multoque magis, accedente ipsa HK, tangentes omnes inter A & B comprehensae arcu eodem AN majores erunt. Si vero GH à centro longius distat quam EF, erit tangens KH major arcu HFGa naar margenoot*, & tangens ML ut ante major arcu LH, & tangens ON major arcu NL, & omnes proinde tangentes ON, ML, KH majores arcu NF. Sed & tangens ED major est arcu suo FDGa naar margenoot*, & tangens CA major similiter arcu suo DA. Itaque tangentes omnes inter BO & A, praeter GF, majores erunt arcu NA; multoque magis tangentes eaedem, accedente GF, hoc est, omnes quae inter BO & A interjiciuntur, eodem arcu NA majores erunt. Ex his vero etiam demonstratio manifesta est in casibus aliis, qualiscunque semicircumferentiae arcus accipiatur, quippe cum vel eadem sit ubique, vel pars tantum praecedentis demonstrationis. | |||||||||||||||||||||||||||||||
Propositio XXI.Si mobile descendat continuato motu per quaelibet plana inclinata contigua, ac rursus ex pari altitudine descendat per plana totidem contigua, ita comparata ut singula altitudine respondeant singulis priorum planorum, sed majori quam illa sint inclinatione. Dico tempus descensus per minus inclinata, brevius esse tempore descensus per magis inclinata. 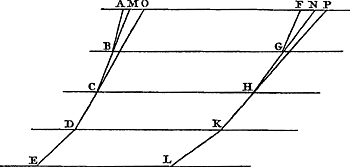 [Fig. 44.]
Sint series duae planorum inter easdem parallelas horizontales com prehensae A B C D E, F G H K L [Fig. 44], atqueita ut bina quaeque sibi correspondentia plana utriusque seriei iisdem parallelis horizontalibus includantur; unumquodque vero seriei FGHKLGa naar voetnoot1) magis inclinatum sit ad horizontem quam planum sibi altitudine respondens feriei ABCDE. Dico breviori tempore absolvi descensum per ABCDE, quam per FGHKL.
Nam primo quidem tempus descensus per AB, brevius esse constat tempore descensusGa naar margenoot+ per FG, quum sit eadem ratio horum temporum quae rectarum AB ad FGGa naar margenoot*, sitque AB minor quam FG, propter minorem inclinationem. Producantur jam sursum rectae | |||||||||||||||||||||||||||||||
[pagina 166]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ geons maintenant vers le haut les droites CB et HG et puissent-elles couper l'horizontale AF en M et N. Par conséquent le temps nécessaire pour parcourir BC après AB est égal à celui du temps nécessaire pour parcourir la même longueur BC après MB, puisqu'au point B le corps a une même vitesse, qu'il soit descendu par AB ou par MBGa naar margenoot*. De la même manière le temps par GH après FG sera égal au temps correspondant à la même longueur GH après NG. Or, le temps par BC après MB est au temps par GH après NG, comme sont entre elles les longueurs BC et GH ou CM et HN, vu que c'est là la valeur du rapport des temps correspondant tant aux longueurs totales MC et NH qu'aux parties MB et NGGa naar margenoot*, donc aussi celui des différences des temps. Or, BC est plus petite que GH à cause de son inclinaison moindre. Il est donc évident que le temps par BC après MB ou après AB est plus court que le temps par GH après NG ou après FG. On démontrera de la même manière, en prolongeant DC et KH vers le haut, jusqu'à ce qu'elles rencontrent l'horizontale AF en O et en P, que le temps par CD après ABC ou après OC est plus court que le temps par HK après FGH ou après PH. Et enfin que le temps par DE après ABCD est plus court que le temps par KL après FGHK. C'est pourquoi le temps de la descente totale par ABCDE sera plus court que le temps par FGHKL. C. Q. F. D. Or, il est manifeste par là, si l'on considère les lignes courbes comme composées d'une infinité de lignes droites, que lorsqu'on a affaire à deux surfaces inclinées suivant des lignes courbées de la même hauteur et dont l'inclinaison de l'une surpasse toujours celle de l'autre en des points quelconques de même hauteur, le corps descendra alors aussi en un temps plus court le long de la surface moins inclinée que le long de la plus inclinée. Supposons par exemple que les deux surfaces [Fig. 45] soient inclinées suivant les courbes AB et CD de même hauteur et pour lesquelles, lorsqu'on prend des points quelconques E, F de même hauteur, l'inclinaison de CD surpasse celle de AB, en d'autres termes que la tangente à la courbe CD en F soit plus inclinée par rapport à l'horizon que la tangente en E à la courbe AB: le temps de la chute par AB sera plus court que celui de la chute par CD. Et la même chose aura lieu lorsque l'une des lignes est droite, pourvu que l'inclinaison partout égale de la droite soit plus grande ou plus petite que celle de la courbe en chacun de ses points. | |||||||||||||||||||||||||||||||
Proposition XXII.Si l'on considère dans une cycloïde à axe vertical, ayant son sommet en bas, deux parties de même hauteur de la courbe, mais dont l'une est plus proche du sommet, le temps de descente par la partie supérieure sera plus petite que celui de la descente par la partie inférieure.
Soit AB [Fig. 46] la cycloïde à axe vertical AC dont le sommet A se trouve en bas. | |||||||||||||||||||||||||||||||
[pagina 167]
| |||||||||||||||||||||||||||||||
CB, HG, occurrantque horizontali AF in M & N. Itaque tempus per BC post AB,Ga naar margenoot+ aequale est tempori per eandem BC post MB, cum in puncto B eadem celeritas contingat, sive per AB, sive per MB descendentiGa naar margenoot*. similiterque tempus per GH post FG, aequale erit tempori per eandem GH post NG. Est autem tempus per BC post MB ad tempus per GH post NG, ut BC ad GH longitudine, sive ut CM ad HN, cum hanc rationem habeant & tempora per totas MC, NH, & per partes MB, NGGa naar margenoot*, ideoque etiam tempora reliqua. Estque BC, minor quam GH propter minorem inclinationem. Patet igitur tempus per BC post MB sive post AB, brevius esse tempore per GH post NG sive post FG. Similiter ostendetur, productis DC, KH sursum, donec occurrant horizontali AF in O & P, tempus per CD post ABC, sive post OC, brevius esse tempore per HK post FGH sive post PH. Ac denique tempus per DE post ABCD, brevius esse tempore per KL post FGHK. Quare totum tempus descensus per ABCDE, brevius erit tempore per FGHKL. quod erat demonstrandum. Hinc vero manifestum est, considerando curvas lineas tanquam ex innumeris rectis compositas, si fuerint duae superficies, secundum lineas curvas ejusdem altitudinis inclinatae, quarum in punctis quibuslibet aeque altis major semper sit inclinatio unius quam reliquae, etiam tempore breviori per minus inclinatam grave descensurum quam per magis inclinatam.
compositas, si fuerint duae superficies, secundum lineas curvas ejusdem altitudinis inclinatae, quarum in punctis quibuslibet aeque altis major semper sit inclinatio unius quam reliquae, etiam tempore breviori per minus inclinatam grave descensurum quam per magis inclinatam.
Velut si sint duae superficies [Fig. 45] inclinatae secundum curvas AB, CD, aequalis altitudinis, quarumque in punctis aeque altis quibuslibet E, F, major sit inclinatio ipsius CD quam AB, hoc est, ut | recta tangens curvam CD in F, magisGa naar margenoot+ inclinata sit ad horizontem, quam quae curvam AB tangit in puncto E. erit tempus descensus per AB brevius quam per CD. Idemque continget si altera linearum recta fuerit: dummodo inclinatio rectae, quae ubique est eadem, major minorve fuerit inclinatione curvae in quolibet sui puncto. | |||||||||||||||||||||||||||||||
Propositio XXII.Si in Cycloide cujus axis ad perpendiculum erectus stat, vertice deorsum spectante, duae portiones curvae aequalis altitudinis accipiantur, sed quarum altera propior sit vertici; erit tempus descensus per superiorem, brevius tempore per inferiorem.
Sit Cyclois AB [Fig 46], cujus axis AC ad perpendiculum erectus, vertex A deor- | |||||||||||||||||||||||||||||||
[pagina 168]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Prenons dans elle les parties BD et EF de même hauteur, c.à.d. telles que les parallèles horizontales BC et DH, comprenant entre elles la partie supérieure BD, soient à égale distance l'une de l'autre que EG et FK qui comprennent entre elles la partie inférieure EF. Je dis que le temps de la descente par la courbe BD sera plus court que celui de la descente par EF. En effet, prenons sur BD le point quelconque L et sur EF le point M de telle manière que la hauteur de E au-dessus de M soit la même que celle de B au-dessus de L. Puissent les horizontales LN et MO rencontrer en N et en O la demi-circonférence décrite sur l'axe AC; tirons encore les droites NA et OA. Comme le point N est plus élevé que le point O, il est donc manifeste que la droite NA possède par rapport à l'horizon une moindre inclinaison que la droite OA. Or, la tangente à la courbe au point L est parallèle à NAGa naar margenoot*, et celle en M est parallèle à OA. Par conséquent la courbe BD est moins inclinée au point L que la courbe EF au point M. Si l'on suppose donc la partie EF, sans que son inclinaison soit changée, élevée plus haut, par exemple en ef, de sorte qu'elle soit comprise entre les mêmes parallèles que la portion BD, le point M sera trouvé en m à la même hauteur que le point L. Dans ce cas l'inclinaison de la courbe ef au point m, qui est égale à celle de la courbe EF en M, sera donc plus grande que celle de la courbe BD en L. Semblablement, dans le cas de n'importe quel autre point de la courbe ef, on démontrera que son inclinaison est plus grande que celle de la courbe BD en un point de même hauteur. Le temps de la descente par BD sera donc plus court que celui de la descente par efGa naar margenoot*, ou bien, ce qui est la même chose, par EF. C. Q. F. D. | |||||||||||||||||||||||||||||||
Lemme.Soit un cercle de diamètre AC [Fig. 47] que DE coupe à angles droits, et puisse une droite AB partant de l'extrémité A du diamètre couper la circonférence en B et DE en F. Je dis que les trois grandeurs AB, AD et AF sont proportionnelles entre elles.
Supposons d'abord que le point d'intersection F soit situé au dedans du cercle, et | |||||||||||||||||||||||||||||||
[pagina 169]
| |||||||||||||||||||||||||||||||
sum spectet; & accipiantur in ea portiones BD & EF, aequalis altitudinis, hoc est,Ga naar margenoot+ ejusmodi ut parallelae horizontales BC, DH, quae superiorem portionem BD includunt, aeque inter | se distent ac EG, FK, inferiorem portionem EF includentes. Dico tempusGa naar margenoot+ descensus per curvan BD brevius fore tempore per EF. Sumatur enim in BD punctum quodlibet L, & in EF punctum M, ita ut eadem sit altitudo E supra M quae B supra L. Et descripto super axe AC semicirculo, occurrant ei rectae horizontales LN, MO, in N & O, & jungantur NA, OA. Itaque quum punctum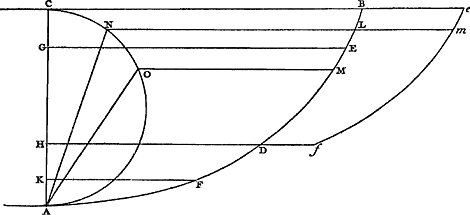 N sit altius puncto O, manifestum est rectam NA minus ad horizontem inclinari quam OA. Est autem ipsi NA parallela tangens curvae in L punctoGa naar margenoot*, & ipsi OA parallela tangens curvae in M. Ergo curva BD in puncto L minus inclinata est quam curva EF in puncto M. Quod si igitur portio EF, invariata inclinatione, altius extolli intelligatur velut in ef, ita ut inter easdem parallelas cum portione BD comprehendatur, invenietur punctum M in m, aequali altitudine cum puncto L. eritque etiam inclinatio curvae ef in puncto m, quae eadem est inclinationi curvae EF in M, major inclinatione curvae BD in L. Similiter vero, & in quolibet alio puncto curvae ef, major ostendetur inclinatio quam curvae BD in puncto aeque alto. Itaque tempus descensus per BD brevius erit tempore per efGa naar margenoot*, sive, quod idem est, per EF. quod erat demonstrandum.
N sit altius puncto O, manifestum est rectam NA minus ad horizontem inclinari quam OA. Est autem ipsi NA parallela tangens curvae in L punctoGa naar margenoot*, & ipsi OA parallela tangens curvae in M. Ergo curva BD in puncto L minus inclinata est quam curva EF in puncto M. Quod si igitur portio EF, invariata inclinatione, altius extolli intelligatur velut in ef, ita ut inter easdem parallelas cum portione BD comprehendatur, invenietur punctum M in m, aequali altitudine cum puncto L. eritque etiam inclinatio curvae ef in puncto m, quae eadem est inclinationi curvae EF in M, major inclinatione curvae BD in L. Similiter vero, & in quolibet alio puncto curvae ef, major ostendetur inclinatio quam curvae BD in puncto aeque alto. Itaque tempus descensus per BD brevius erit tempore per efGa naar margenoot*, sive, quod idem est, per EF. quod erat demonstrandum.
| |||||||||||||||||||||||||||||||
[pagina 170]
| |||||||||||||||||||||||||||||||
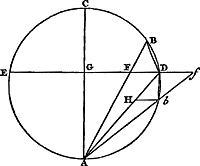 [Fig. 47.]
Ga naar margenoot+ tirons la corde correspondant à l'arc BD. Comme les arcs AE et AD sont égaux, les angles inscrits EDA et ABD qui correspondent à ces arcs seront alors également égaux entre eux. Par conséquent dans les triangles ABD et ADF les angles ABD et ADF sont égaux. D'autre part l'angle A est commun aux deux triangles. Les dits triangles seront donc semblables, partant BA : AD = AD : AF. Soit en second lieu le point d'intersection f en dehors du cercle et tirons bH parallèle à DE, laquelle rencontre la droite AD en H. Suivant ce qui a déjà été démontré on aura alors DA : Ab = Ab : AH, en d'autres termes = Af : AD. Par conséquent Af, AD et Ab formeront dans ce cas aussi une proportion. Ainsi la proposition est établie. | |||||||||||||||||||||||||||||||
Proposition XXIII.Soit la cycloïde ABC [Fig. 48] ayant son sommet vers le bas et son axe AD vertical. Prenons sur elle un point quelconque B et tirons de là vers le bas la droite BI qui touche la cycloïde et se termine à la droite horizontale AI. Tirons la droite BF perpendiculairement à l'axe et décrivons sur FA, après l'avoir divisée en deux parties égales par le point X, la demi-circonférence FHA. La droite ΣG ayant été ensuite menée parallèlement à BF par un point quelconque G pris sur la courbe BA, laquelle ΣG coupe la circonférence FHA en H et l'axe AD en Σ, considérons les tangentes aux deux courbes aux points G et H et les parties de ces tangentes interceptées par les mêmes deux horizontales MS et NT, savoir MN et ST. Et puissent les mêmes droites MS et NT intercepter sur la tangente BI la partie OP et sur l'axe DA la partie QR. Cela étant ainsi, je dis que le temps dans lequel un corps parcourra la droite MN avec une vitesse constante telle qu'il peut l'acquérir en descendant par l'arc BG de la | |||||||||||||||||||||||||||||||
[pagina 171]
| |||||||||||||||||||||||||||||||
Quia igitur arcus aequales sunt AE, AD, erunt anguli ad circumferentiam ipsis insistentes,Ga naar margenoot+ EDA, ABD aequa|les. Itaque in triangulis ABD, ADF, aequales anguli ABD,Ga naar margenoot+ ADF. Communis autem utrique est angulus ad A. Ergo dicti trianguli similes erunt, ideoque BA ad AD ut AD ad AF. Sit jam punctum intersectionis f extra circulum, & ducatur bH parallela DE, quae occurrat rectae AD in H. Itaque secundum jam demonstrata erit ut DA ad Ab, ita Ab ad AH, hoc est, ita Af ad AD: Ideoque rursus proportionales erunt Af, AD, Ab. Quare constat propositum. | |||||||||||||||||||||||||||||||
Propositio XXIII.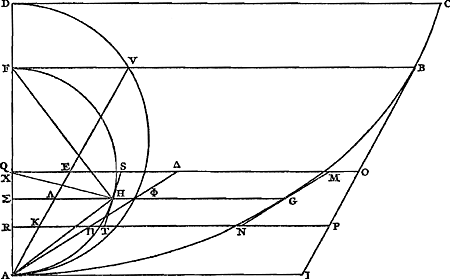 [Fig. 48.]
Sit Cyclois ABC [Fig. 48], cujus vertex A deorsum conversus sit, axe AD ad perpendiculum erecto; sumptoque in ea quolibet puncto B, ducatur inde deorsum recta BI quae Cycloidem tangat, termineturque recta horizontali AI. recta vero BF ad axem perpendicularis agatur, & divisa bifariam FA in X, super ea describatur semicirculus FHA. Ductâ deinde per punctum quodlibet G in curva BA sumptum, rectâ ΣG parallelâ BF, quae circumferentiae FHA occurrat in H, axi AD in Σ, intelligantur per puncta G & H rectae tangentes utriusque curvae, earumque tangentium partes iisdem duabus horizontalibus MS, NT interceptae sint MN, ST. Iisdemque rectis MS, NT includantur tangentis BI pars OP, & axis DA pars QR. Quibus ita se habentibus, dico tempus quo grave percurret rectam MN, celeritate aequabili quanta acquiritur descendendo per arcum Cycloidis BG, fore ad tempus | |||||||||||||||||||||||||||||||
[pagina 172]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ cycloïde, sera au temps dans lequel la droite OP sera parcourue avec une vitesse constante égale à la moitié de celle qui est acquise par la descente le long de la tangente BI, comme la tangente ST est à la partie QR de l'axe.
En effet, décrivons sur l'axe AD la demi-circonférence DVA coupant la droite BF en V et ΣG en Φ, et tirons la droite AV qui coupe les droites OQ, PR et GΣ en E, K et Λ. Tirons encore HF, HA, HX et AΦ, dont la dernière coupe les droites OQ et PR aux points ∆ et II. Le temps par HN dont nous avons parlé a donc au temps par OP une raison composée du rapport des lignes MN et OP elles-mêmes et de l'inverse du rapport des vitesses avec lesquelles elles sont parcouruesGa naar margenoot*, le dernier rapport étant celui de la moitié de la vitesse provenant d'une chute selon BI ou FA à la vitesse provenant d'une chute suivant BG ou FΣGa naar margenoot*. Mais la vitesse totale provenant de la chute FA est à la vitesse correspondant à la chute FΣ dans un rapport égal à celui des racines carrées des longueurs FA et FΣGa naar margenoot* et par conséquent la même que celui de FA à FH. La moitié de la vitesse provenant de la chute FA est donc à la vitesse provenant de la chute FΣ comme FX est à FH. Le temps susdit par MN aura donc au temps par OP une raison composée des rapports MN : OP et FX : FH. Or, nous démontrerons que le premier de ces rapports, savoir MN : OP, est égal à FH : HΣ. En effet, la tangente BI à la cycloïde est parallèle à la droite VA et de même la tangente MGN à la droite ΦA; par conséquent la droite MN est égale à ΔΠ et OP à EK. Le dit rapport de la droite MN à OP est donc égal à celui de ΔΠ à EK, en d'autres termes à celui de ∆A à EA, c.à.d. de Φ A à ΛA, c.à.d. de VA à ΦAGa naar margenoot*. Mais VA : ΦA = FA : AH; car, attendu que le carré de VA est égal au rectangle DAF, et le carré de AΦ au rectangle DAΣ, lesquels rectangles sont entre eux dans le rapport FA : ΣA, ou FA2 : AH2, il s'ensuit que VA2 : ΦA2 = FA2 : AH2 ou, en considérant les longueurs, VA : AΦ = FA : AH. Le rapport MN : OP est donc égal à FA : AH, c.à.d., à cause de la similitude des triangles FAH et FHΣ, à FH : HΣ, comme il a été dit. Par conséquent la dite raison du temps par MN au temps par OP est composée des rapports FX : FH et FH : HΣ; elle sera donc la même que celle de FX ou XH à HΣ. Mais comme le rayon XH est à HΣ, ainsi est la tangente ST à la droite QR; c'est une chose qu'on voit facilement. Partant il est établi que le temps du mouvement considéré par MN est au temps du mouvement par OP comme ST est à QR. C. Q. F. D. | |||||||||||||||||||||||||||||||
Proposition XXIV.Considérons de nouveau, comme dans la Proposition précédente, la cycloïde ABC [Fig. 49] dont le sommet se trouve en bas et dont l'axe AD est vertical. Prenons sur elle un point quelconque B et tirons à partir de lui de haut en bas la tangente à la cycloïde BΘ qui rencontre la droite horizontale AΘ en Θ. Tirons encore la droite BF perpendiculaire à l'axe et décrivons sur FA la demi-circonférence FHA. Puisse en- | |||||||||||||||||||||||||||||||
[pagina 173]
| |||||||||||||||||||||||||||||||
quo percurretur recta OP, celeritate aequabili dimidia ejus quae acquiritur descendendoGa naar margenoot+ per totam tangentem BI, sicut est tangens ST ad partem axis QR.
Describatur enim super axe AD semicirculus DVA secans rectam BF in V, & ΣG in Φ, & jungatur AV secans rectas OQ, PR, GΣ in EK & Λ. Jungantur item HF, HA, HX & AΦ; quae postrema secet rectas OQ, PR in punctis Δ & Π. Habet ergo dictum tempus per MN ad tempus per OP, rationem eam quae componitur ex ratione ipsarum linearum MN ad OP, & ex ratione celeritatum quibus ipsae percurruntur, contrarie sumptaGa naar margenoot*, hoc est, & ex ratione dimidiae celeritatis ex BI sive ex FA, ad celeritatem ex BG, sive ex FΣGa naar margenoot*. Atqui tota celeritas ex | FA ad celeritatemGa naar margenoot+ ex FΣ, est in subduplicata ratione longitudinum FA ad FΣGa naar margenoot*, ac proinde eadem quae FA ad FH. Ergo dimidia celeritas ex FA ad celeritatem ex FΣ erit ut FX ad FH. Itaque tempus dictum per MN ad tempus per OP habebit rationem compositam ex rationibus MN ad OP, & FX ad FH. Harum vero prior ratio, nempe MN ad OP, eadem ostendetur quae FH ad HΣ. Est enim tangens Cycloidis BI parallela rectae VA, similiterque tangens MGN parallela rectae ΦA; ac proinde recta MN aequalis ΔΠ, & OP aequalis EK. Ergo dicta ratio rectae MN ad OP eadem est quae ΔΠ ad EK; hoc est, ∆A ad EA; hoc est, ΦA ad ΛA; hoc est VA ad ΦAGa naar margenoot*. Est autem ut VA ad AΦ ita FA ad AH; nam quia quadratum VA aequale est rectangulo DAF, & quadratum AΦ aequale rectangulo DAΣ, quae rectangula sunt inter se ut FA ad ΣA, hoc est ut quadratum FA ad quadratum AH, erit proinde & quadratum VA ad quadratum ΦA ut quadratum FA ad quadratum AH; atque etiam VA ad AΦ longitudine, ut FA ad AH. Ratio itaque MN ad OP, eadem erit quae FA ad AH, hoc est, propter triangula similia FAH, FHΣ, eadem quae FH ad HΣ, ut dictum fuit. Itaque dicta ratio temporis per MN ad tempus per OP, componitur ex rationibus FX ad FH & FH ad HΣ, ideoque eadem erit quae FX sive XH ad HΣ. Sicut autem radius XH ad HΣ, ita est tangens ST ad rectam QR; hoc enim facile perspicitur. Igitur tempus motus qualem diximus per MN, ad tempus per OP constat esse sicut ST ad QR. quod erat demonstrandum. | |||||||||||||||||||||||||||||||
Propositio XXIV.Ga naar margenoot+Sit rursus ut in praecedenti propositione Cyclois ABC [Fig. 49], cujus vertex A deorsum spectet, axis AD ad horizontem erectus sit; & sumpto in ea quovis puncto B, ducatur inde deorsum recta BΘ quae Cycloidem tangat, occurratque rectae horizontali AΘ in Θ: recta vero BF axem perpendicularis agatur, & super FA describatur semicirculus FHA. Deinde alia recta GE, parallela FB, secet Cycloidem in E, | |||||||||||||||||||||||||||||||
[pagina 174]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ suite une autre droite GE, parallèle à FB, couper la cycloide en E, la droite BΘ en I, la circonférence FHA en H et enfin l'axe DA en G. Je dis que le temps de la descente suivant l'arc de cycloïde BE est à celui suivant la tangente BI avec la moitié de la vitesse qui peut être acquise par une chute suivant BΘ comme l'arc FH est à la droite FG.
En effet, si cela n'est pas vrai, le temps de la chute suivant l'arc BE aura au temps susdit correspondant à BI, un rapport supérieur ou inférieur à celui de l'arc FH à la droite FG. Que le premier temps ait d'abord à l'autre, si cela est possible, un rapport plus grand. Dans ce cas un certain temps plus court que celui de la chute selon BE (que ce soit le temps Z) aura au temps considéré correspondant à BI le rapport de l'arc FH à la droite FG. Que si maintenant on prend sur la cycloïde au-dessus du point B un autre point N, le temps nécessaire pour parcourir BE après NB sera plus court que le temps suivant BE. Or, il est manifeste qu'on peut prendre le point N si près de B, que la différence de ces temps devient aussi petite qu'on veut et qu'elle est par conséquent plus petite que celle dont le temps Z est surpassé par le temps de la chute suivant BE. Supposons donc le point N ainsi choisi. Il s'ensuit que le temps de la chute suivant BE après NB sera plus grand que le temps Z et aura par conséquent au temps de la chute suivant BI avec la moitié de la vitesse qui peut être acquise par une chute suivant BΘ, un rapport supérieur à celui de l'arc FH à la droite FG. Que le premier temps ait donc au deuxième un rapport égal à celui de l'arc FHO à la droite FG. Divisons FG en parties égales FB, PQ, etc. dont chacune correspond à une hauteur moindre que celle de la ligne NB, moindre aussi que celle de l'arc HO; en effet, il est évident que cela est possible. Tirons à partir des points de division des droites PΛ, QΞ, etc. parallèles à la base DC et se terminant à la tangente BΘ. Et soient menées vers le haut, à partir des points où ces parallèles coupent la circonférence FH, et de même à partir du point H, des tangentes chacune jusqu'à la parallèle prochaine, telles que ∆X, ΓΣ, etc. Soient également menées vers le haut à partir des points où | |||||||||||||||||||||||||||||||
[pagina 175]
| |||||||||||||||||||||||||||||||
 [Fig. 49.]Ga naar margenoot+
rectam BΘ in I, circumferentiam FHA in H, & denique axem DA in G. Dico tempus descensus per arcum Cycloidis BE, esse ad tempus per tangentem BI cum celeritate dimidia ex BΘ, sicut arcus FH ad rectam FG.
Si enim hoc verum non est, habebit tempus per arcum BE ad dictum tempus per BI, vel majorem rationem quam arcus FH ad rectam FG vel minorem. Habeat primo, si fieri potest, majorem. Itaque tempus aliquod brevius tempore per BE (sit hoc tempus Z) erit ad dictum tempus per BI ut arcus FH ad rectam FG. Quod si jam in Cycloide supra punctum B sumatur punctum aliud N, erit tempus per BE post NB, brevius tempore per BE. Manifestum est autem punctum N tam propinquum sumi posse ipsi B, ut differentia eorum temporum sit quamlibet exigua, ac proinde ut minor sit ea qua tempus Z superatur à tempore per BE. Sit itaque | punctum N ita sumptum. unde quidem tempusGa naar margenoot+ per BE post NB majus erit tempore Z, majoremque proinde rationem habebit ad tempus dictum per BI cum dimidia celeritate ex BΘ, quam arcus FH ad rectam FG. Habeat itaque eam quam arcus FHO ad rectam FG. Dividatur FG in partes aequales FP, PQ, &c. quarum unaquaeque minor sit altitudine lineae NB, atque item altitudine arcus HO; hoc enim fieri posse manifestum est; & à punctis divisionum agantur rectae, basi DC parallelae, & ad tangentem BΘ terminatae PΛ, QΞ, &c. Quibusque in punctis hae secant circumferentiam FH, ab iis, itemque à puncto H, tangentes sursum ducantur usque ad proximam quaeque parallelam, velut ∆X, ΓΣ &c. Similiter vero & à punctis, in quibus dictae parallelae Cycloidi | |||||||||||||||||||||||||||||||
[pagina 176]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ les dites parallèles coupent la cycloïde, des tangentes telles que SV, TM, etc. Or, si l'on ajoute à la droite FG une partie GR égale à celles qui résultent de la division, et qu'on même RΦ parallèle, comme les autres, à DC, il apparaît que celle-ci coupe la circonférence FHA entre H et O, puisque GR est plus petite que la hauteur du point H au-dessus de O. Et maintenant nous raisonnerons comme suit. Le temps d'une chute suivant la tangente VS avec la vitesse constante qui pourrait être acquise par une chute suivant BS est plus grand que le temps d'un mouvement uniformément accéléré suivant l'arc BS après NB. Car la vitesse résultant de la chute BS est moindre que la vitesse résultant de la chute NB parce que la hauteur de BS est inférieure à celle de NB. Mais la vitesse provenant de la chute BS est supposée ici rester la même durant le trajet de la tangente VS, tandis que la vitesse acquise par la chute selon NB s'accélère continuellement durant le trajet de l'arc BS; de plus ce dernier est plus petit que la tangente VS et partout moins incliné qu'aucune partie de cette tangente. De sorte que pour toutes ces raisons le temps nécessaire pour parcourir la tangente VS avec la vitesse qui correspond à une chute suivant BS est plus grand que le temps nécessaire pour parcourir l'arc BS après une chute suivant NB. Pareillement le temps d'une chute suivant la tangente MT avec une vitesse égale à celle qui résulte d'une chute suivant BT sera plus grand que le temps nécessaire pour parcourir l'arc ST après NS, et le temps employé pour parcourir la tangente ΠY avec une vitesse telle qu'elle provient d'une chute selon BY sera plus grand que le temps nécessaire pour parcourir l'arc TY après NT. Et ainsi la somme des temps des mouvements uniformes suivant toutes les tangentes jusqu'à la plus basse qui touche la cycloïde en E, chacune d'elles étant parcourue avec la vitesse qui peut être acquise par une chute à partir du point B jusqu'à leur point de contact, fera plus grande que le temps nécessaire pour parcourir l'arc BE après NB. Mais cette même somme de temps serait aussi plus petite, comme nous le montrerons maintenant. En effet, considérons de nouveau les mêmes temps des mouvements uniformes suivant les tangentes à la cycloïde. Or, le temps d'une chute suivant la tangente VS avec la vitesse provenant d'une chute suivant BS est au temps nécessaire pour parcourir la droite BΛ avec la moitié de la vitesse telle qu'elle serait acquise par une chute suivant FA, comme la tangente ∆X à la circonférence est à la partie FP de l'axeGa naar margenoot* Pareillement le temps nécessaire pour parcourir la tangente MT avec une vitesse telle qu'elle provient d'une chute suivant BT est au temps nécessaire pour parcourir la droite AΞ avec cette même moitié de la vitesse correspondant à la chute suivant FA, comme la tangente ΓΣ est à la droite PQ. Et ainsi de suite: chacun des temps nécessaires pour parcourir une des tangentes à la cycloïde, lesquels sont les mêmes que ceux considérés plus haut, sera au temps du mouvement uniforme selon la partie de la droite BI qui lui corespond avec la moitié de la vitesse provenant d'une chute BΘ, comme la tangente à la circonférence FH comprise entre les mêmes parallèles est à la partie correspondante de la droite FG. Il y a donc certaines longueurs FP, PQ, etc. et un même nombre d'autres quantités, | |||||||||||||||||||||||||||||||
[pagina 177]
| |||||||||||||||||||||||||||||||
occurrunt, tangentes sursum ducantur velut SV, TM &c. additâ vero ad rectam FGGa naar margenoot+ parte una GR aequali iis quae ex divisione, ductâque RΦ parallelâ similiter ipsi DC, patet eam occurrere circumferentiae FHA inter H & O, quia GR minor est altitudine puncti H supra O. Jam vero sic porro argumentabimur. Tempus per tangentem VS cum celeritate aequabili quae acquireretur ex BS, majus est tempore motus continue accelerati per arcum BS post NB. Nam celeritas ex BS minor est celeritate ex NB, propterea quod minor altitudo BS quam NB. At celeritas ex BS aequabiliter continuari ponitur per tangentem VS, cum celeritas acquisita ex NB continue porro acceleretur per arcum BS, qui arcus minor insuper est tangente VS, omnibusque partibus suis magis erectus quam ulla pars tangentis VS. Adeo ut omnino majus sit futurum tempus per tangentem VS cum celeritate ex BS, tempore per arcum BS post NB. Similiter tempus per tangentem MT, cum celeritate ex BT, majus erit tempore per arcum ST post NS, & tempus per tangentem ΠY cum celeritate ex BY, majus tempore per arcum TY post NT. Atque ita tempora motuum aequabilium per tangentes omnes usque ad infimam quae tangit cycloidem in E, cum celeritatibus per singulas quantae acquiruntur cadendo ex B adusque punctum ipsarum contactus, majora simul erunt tempore per arcum BE post NB. Eadem vero & minora essent, ut nunc ostendemus. Considerentur enim denuo tempora eadem motuum aequabilium per tangentes cycloidis. Et est quidem tempus per tangentem VS cum celeritate ex BS, ad tempus per rectam BA cum celeritate dimidia ex FA, ut tangens circumferentiae ∆X ad partem|axisGa naar margenoot* FPGa naar margenoot+. Similiterque tempus per tangentem MT, cum celeritate ex BT, ad tempus per rectam ΔΞ cum eadem dimidia celeritate ex FA, ut tangens ΓΣ ad rectam PQ. Atque ita deinceps singula tempora per tangentes cycloidis, quae sunt eadem supradictis, erunt ad tempora motus aequabilis per partes sibi respondentes rectae BI cum celeritate dimidia ex BΘ, sicut tangentes circumferentiae FH, iisdem parallelis comprehensae, ad partes rectae FG ipsis respondentes. Sunt igitur quantitates quaedam rectae FP, PQ, &c. & totidem aliae, tempora scili- | |||||||||||||||||||||||||||||||
[pagina 178]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ savoir les temps dans lesquels sont parcourues les droites BΛ, ΛΞ, etc. d'un mouvement uniforme avec la moitié de la vitesse provenant d'une chute suivant BΘ; et chaque quantité de la première série a le même rapport à la quantité suivante que chaque quantité de la deuxième série à celle qui la suit: en effet, les quantités de chacune des séries sont égales entre elles. Or, les rapports des quantités de la première série à certaines autres, savoir aux tangentes ∆X, ΓΣ, etc. à la circonférence, sont les mêmes et observent le même ordre que les rapports des quantités de la deuxième série à certaines autres, savoir aux temps du mouvement susdit le long des tangentes VS, MT, etc. à la cycloïde. Par conséquent, comme se rapporte la somme de toutes les premières à celle des grandeurs correspondantes, c.à.d. comme la ligne FG entière est à la somme de toutes les tangentes X∆, ΓZ, etc., ainsi est le temps dans lequel la tangente entière BI est parcourue avec la moitié de la vitesse acquise par une chute suivant BΘ, à la somme de tous les temps correspondants aux mouvements susdits suivant les tangentes VS, MT, etc. à la cycloïdeGa naar margenoot*. Ainsi donc, par inversion, les temps des mouvements susdits suivant les tangentes à la cycloïde auront au temps nécessaire pour parcourir la droite BI avec la moitié de la vitesse qui résulterait d'une chute suivant BΘ, la même raison que toutes les tangentes à la circonférence FH à la droite FG, et par conséquent une raison moindre que celle de l'arc FO à la même droite FG, puisque l'arc FΦ, et par conséquent a-fortiori l'arc FO, est plus grand que l'ensemble des tangentes à l'arc FHGa naar margenoot*. Mais nous avons posé que le temps nécessaire pour parcourir BE après NB est au temps nécessaire pour parcourir BI avec la moitié de la vitesse qui résulterait d'une chute selon BΘ, comme l'arc FO est à la droite FG. Par conséquent la somme des temps nécessaires pour parcourir chacune des tangentes à la cycloïde sera plus petite que le temps nécessaire pour parcourir BE après NB, tandis qu'auparavant nous avons démontré que cette somme est plus grande; ce qui est absurde. Il en résulte que le temps nécessaire pour parcourir l'arc de cycloïde BE n'a pas au temps de parcourir la tangente BI avec la moitié de la vitesse provenant d'une chute selon BΘ ou FA, un rapport supérieur à celui de l'arc FH de la circonférence à la droite FG. Supposons maintenant, si cela est possible, que le premier temps ait au deuxième un rapport inférieur au dernier rapport nommé. Par conséquent un certain temps supérieur au temps nécessaire pour parcourir l'arc BE (que ce soit le temps Z) sera au temps considéré correspondant à BI comme l'arc FH est à la droite FG. Or, si l'on prend [Fig. 50] un arc NM égal en hauteur à l'arc BE, mais dont l'extrémité supérieure N soit située au-dessous du point B, le temps de chute le long de l'arc NM sera plus grand que le temps correspondant pour l'arc BEGa naar margenoot*. Il est évident que le point N peut être pris si près du point B que la différence des dits temps devient aussi petite qu'on veut, et par conséquent inférieure à celle dont le temps Z surpasse le temps nécessaire pour parcourir l'arc BE. Supposons donc le point N choisi de cette manière. Dans cette hypothèse le temps de la chute suivant NM sera inférieur au temps Z, et aura par conséquent au dit temps correspondant à BI, sup- | |||||||||||||||||||||||||||||||
[pagina 179]
| |||||||||||||||||||||||||||||||
cet quibus percurruntur rectae BΛ, ΛΞ &c, motu aequabili cum celeritate dimidia exGa naar margenoot+ BΘ; Et unaquaeque quantitas in prioribus ad sequentem eadem proportione refertur, qua unaquaeque posteriorum ad suam sequentem; sunt enim utrobique inter se aequales. Quibus autem proportionibus priores quantitates ad alias quasdam, nempe ad tangentes circuli ∆X, ΓΣ, &c, referuntur, iisdem proportionibus & eodem ordine posteriores quoque referuntur ad alias quasdam, nempe ad tempora motus qualem diximus per tangentes cycloidis VS, MT &c. Ergo, sicut se habent omnes simul priores ad omnes eas ad quas ipsae referuntur, hoc est, sicut tota FG ad tangentes omnes X∆, ΓΣ, &c. ita tempus quo percurritur tota BI cum celeritate dimidia ex BΘ, ad tempora omnia motuum quales diximus per tangentes cycloidis VS, MT, &cGa naar margenoot* Et invertendo itaque, tempora motuum dictorum per tangentes cycloidis, ad tempus per rectam BI cum celeritate dimidia ex BΘ, eandem rationem habebunt quam dictae tangentes omnes circumferentiae FH ad rectam FG; ac minorem proinde quam arcus FO ad rectam eandem FG; quia arcus FΦ, ideoque omnino & arcus FO major est dictis omnibus arcus FH tangentibusGa naar margenoot*. Atqui tempus per BE post NB, ad tempus per BI cum celeritate dimidia ex BΘ, posuimus esse ut arcus FO ad rectam FG. Ergo dicta tempora omnia per tangentes cycloidis minora fimul erunt tempore per BE post NB, cum antea majora esse ostensum sit; quod est absurdum. Itaque tempus per arcum cycloidis BE, ad tempus per tangentem BI, cum celeritate dimidia ex BΘ vel ex FA, non habet majorem rationem quam arcus circumferentiae FH ad rectam FG. Habeat jam, si potest, minorem. Ergo tempus aliquod majus tempore per arcum BE, (sit hoc tempus Z) erit ad tempus dictum per BI, ut arcus FH ad rectam FG. Quod si jam sumatur [Fig. 50] arcus NM aequalis altitudine cum arcu B|E, sedGa naar margenoot+ cujus terminus superior N sit humilior puncto B, erit tempus per arcum NM majus tempore per arcum BEGa naar margenoot*. Manifestum autem quod punctum N tam propinquum sumi potest puncto B, ut differentia distorum temporum sit quamlibet exigua, ac proinde minor ea qua tempus Z superat tempus per arcum BE. Sit itaque punctum N ita sumptum. Unde quidem tempus per NM minus erit tempore Z, habebitque proinde ad dictum tempus per BI, cum dimidia celeritate ex BΘ, minorem rationem quam | |||||||||||||||||||||||||||||||
[pagina 180]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ posé parcourue avec la moitié de la vitesse qui résulterait d'un chute suivant BΘ, un rapport inférieur à celui de l'arc FH à la droite FG. Que le premier temps ait donc au deuxième un rapport égal à celui de l'arc LH à la droite FG. Divisons maintenant FG en des parties égales FP, PQ, etc. dont chacune soit inférieure à la hauteur de l'arc de cycloïde BN et en même temps à celle de l'arc de circonférence FL; et tirons, après avoir ajouté à FG une de ces parties Gζ, à partir des points de division des droites parallèles à la base DC et se terminant à la tangente BΘ, savoir PO, QK, etc. et de même à partir du point ζ la droite ζΩ coupant la cycloïde en V et la circonférence en η. Menons ensuite vers le bas à partir des points où les dites parallèles coupent la circonférence FH, des tangentes chacune jusqu'à la parallèle prochaine, telles que θΔ et ΓΣ, dont la plus basse partant du point H rencontre la droite ζΩ en X. Menons de plus également vers le bas, à partir des points où les dites parallèles coupent la cycloïde, un nombre égal de tangentes, telles que SΛ, TΞ, etc. dont la plus basse, savoir la tangente au point E, rencontre la droite ζΩ en R. Comme Pζ est égale à FG, hauteur de l'arc BE, à laquelle est égale d'après la construction celle de l'arc NM, Pζ sera aussi égale à la hauteur de l'arc NM. Or, la droite PO est, d'après la construction, située plus haut que l'extrémité N. Par conséquent ζΩ, et son point V, seront situés plus haut que l'extrémité M. C'est pourquoi, l'arc SV étant égal en hauteur à l'arc NM, mais ayant son extrémité S située au-dessus de N, le temps d'une chute suivant SV sera plus court que celui d'une chute suivant NMGa naar margenoot*. Mais le temps nécessaire pour parcourir la tangente SΛ avec la vitesse constante considérée, savoir celle qui provient d'une chute suivant BS, est plus court que le temps d'une chute accélérée le long de l'arc ST commençant en S. Car la vitesse provenant d'une chute suivant BS, avec laquelle toute la droite SΛ est parcourue par hypothèse, est égale à la vitesse provenant d'une chute suivant STGa naar margenoot*, c.à.d. à la vitesse acquise à la fin par le mouvement suivant cet arc ST, et SΛ est plus petite que ST. Pareillement le temps nécessaire pour parcourir la tangente TΞ avec une vitesse constante, savoir celle qui provient de la chute suivant BT, est plus court que le temps d'une chute accélérée suivant l'arc TY après ST, vu que la vitesse provenant de la chute suivant BT, avec laquelle toute la droite TΞ est parcourue par hypothèse, est égale à la vitesse provenant d'une chute suivant SY, c.à.d. à la | |||||||||||||||||||||||||||||||
[pagina 181]
| |||||||||||||||||||||||||||||||
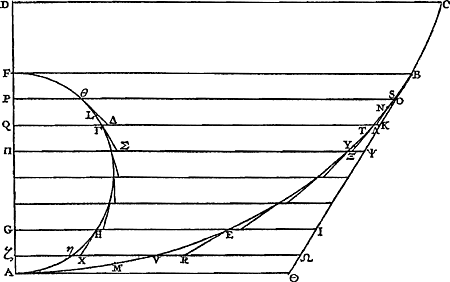 [Fig. 50.]Ga naar margenoot+
arcus FH ad rectam FG. Habeat ergo eam quam arcus LH ad rectam FG. Dividatur jam FG in partes aequales FP, PQ, &c. quarum unaquaeque minor sit arcus cycloidis BN altitudine, itemque minor altitudine arcus circumferentiae FL; & additâ ad FG unâ earum partium Gζ, ducantur à punctis divisionum rectae basi DC parallelae, & ad tangentem BΘ terminatae, PO, QK, &c; itemque à puncto ζ recta ζΩ quae secet cycloidem in V, circumferentiam in η; quibusque in punctis ductae parallelae secant circumferentiam FH, ab iis tangentes deorsum ducantur usque ad proximam quaeque parallelam, velut θΔ, ΓΣ: Quarum infima à puncto H ducta occurrat rectae ζΩ in X. Similiter vero & à punctis, in quibus dictae parallelae occurrunt cycloidi, ducantur totidem tangentes deorsum, velut SΛ, ΤΞ, &c. quarum infima, tangens nempe à puncto E ducta, occurrat rectae ζΩ in R. Quia igitur Pζ aequalis est FG altitudini arcus BE, cui aequalis est ex constructione altitudo arcus NM, erit & Pζ aequalis altitudini arcus NM. Est autem recta PO ex constructione superior ter|mino N. Ergo & ζΩ, & in ea punctum V, superius terminoGa naar margenoot+ M. Quare, cum arcus SV aequalis sit altitudinis cum arcu NM, sed termino S sublimiore quam N, erit tempus per SV brevius tempore per NMGa naar margenoot*. Atqui tempus per tangentem SΛ, cum celeritate aequabili ex BS, brevius est tempore descensus accelerati per arcum ST, incipientis in S. Nam celeritas ex BS, qua tota SΛ transmissa ponitur, aequalis est celeritati ex STGa naar margenoot*, quae motui per arcum ST in fine demum acquiritur; ipsaque SΛ minor est quam ST. Similiter tempus per tangentem ΤΞ, cum celeritate aequabili ex BT, brevius est tempore descensus accelerati per arcum TY post ST; quum celeritas ex BT, qua tota ΤΞ transmissa ponitur, sit aequalis cele- | |||||||||||||||||||||||||||||||
[pagina 182]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ vitesse acquise à la fin par le dit mouvement suivant l'arc TY après ST, et que la droite TΞ est inférieure en longueur à l'arc TY. Par conséquent la somme de tous les temps qui correspondent aux mouvements uniformes le long des tangentes à la cycloïde avec les vitesses qui sont obtenues, dans le cas de chacune d'elles, par une chute à partir du point B jusqu'à son point de contact, sera inférieure au temps d'une chute accéléree le long de l'arc SV. Mais cette même somme serait aussi plus grande que ce dernier temps, comme nous le démontrerons maintenant. En effet, le temps considéré nécessaire pour parcourir la tangente SΛ, avec une vitesse constante, savoir celle qui provient d'une chute suivant BS, est au temps nécessaire pour parcourir la droite OK avec la moitié de la vitesse provenant d'une chute suivant BΘ, comme la tangente à la demi-circonférence θΔ est à la droite PQGa naar margenoot*. De même le temps de parcourir la tangente TΞ avec la vitesse uniforme considérée, savoir celle qui provient d'une chute suivant BT, est au temps nécessaire pour parcourir uniformément la droite KΨ avec la moitié de la vitesse provenant de la chute suivant BΘ, comme la tangente ΓΣ est à la droite QΠ. Et ainsi de suite: les temps nécessaires pour parcourir les tangentes à la cycloïde, qui sont les mêmes que précédemment, seront chacun au temps d'un mouvement uniforme suivant la partie correspondante de la droite OΩ, avec la moitié de la vitesse provenant de la chute suivant BΘ, comme la tangente à la circonférence θη comprise entre les mêmes parallèles est à la partie correspondante de la droite Pζ. D'où l'on conclura, comme dans la première partie de la démonstration, que la somme de toutes les droites PQ, QΠ, etc. c.à.d. la ligne entière Pζ, est à la somme des tangentes θΔ, ΓΣ, etc. comme le temps dans lequel est parcourue toute la tangente OΩ, avec la moitié de la vitesse provenant d'une chute suivant BΘ, à la somme totale des mouvements susdits suivant les tangentes à la cycloïde SΛ, TΞ, etc. Par conversion, on aura donc aussi que la somme des temps suivant les tangentes à la cycloïde aura au temps susdit du mouvement uniforme suivant la droite OΩ, ou bien suivant BI, le même rapport que la somme des dites tangentes à l'arc θη à la droite Pζ ou FG; ce rapport des temps sera donc supérieur à celui de l'arc LH à la droite FG; en effet, l'arc θH, et à plus forte raison l'arc LH, sera plus petit que la dite somme des tangentes à l'arc θηGa naar margenoot*. Mais nous avons supposé dès le commencement que le temps nécessaire pour parcourir NM se rapporte à celui de BI comme l'arc LH est à la droite FG. Par conséquent le temps de parcourir NM et à plus forte raison celui de parcourir SV sera inférieur au temps de parcourir l'ensemble des tangentes à la cycloïde. Ce qui est absurde puisqu'il a été démontré plus haut que ce temps est inférieur à celui correspondant à une chute suivant l'arc SV. Il est donc évident que le temps d'une chute suivant l'arc de cycloïde BE est au temps nécessaire pour parcourir uniformément la tangente BI avec la moitié de la vitesse provenant d'une chute suivant BΘ, dans un rapport qui n'est pas inférieur à celui de l'arc FH à la droite FG. Mais il a également été démontré que le rapport des temps n'est pas plus grand que ce dernier. Il est donc nécessaire qu'il ait la même valeur. C. Q. F. D. | |||||||||||||||||||||||||||||||
[pagina 183]
| |||||||||||||||||||||||||||||||
ritati ex SY, quae in fine demum acquiritur motui dicto per arcum TY post ST; ipsaqueGa naar margenoot+ ΤΞ minor sit arcu TY. Atque ita tempora omnia motuum aequabilium per tangentes cycloidis, cum celeritatibus per singulas quantae acquiruntur descendendo ex B usque ad punctum ipsarum contactus, breviora simul erunt tempore descensus accelerati per arcum SV. Eadem vero & longiora essent, ut nunc ostendemus. Est enim tempus dictum per tangentem SΛ, cum celeritate aequabili ex BS, ad tempus per rectam OK cum celeritate aequabili dimidia ex BΘ, sicut tangens semicirculi θΔ ad rectam PQGa naar margenoot*. similiterque tempus per tangentem ΤΞ, cum celeritate aequabili ex BT, est ad tempus per rectam ΚΨ cum celeritate aequabili dimidia ex ΒΘ, ut tangens ΓΣ ad rectam QΠ. Atque ita deinceps singula tempora per tangentes cycloidis, quae sunt eadem supra dictis, erunt ad tempora motus aequabilis per partes sibi respondentes rectae ΟΩ, cum celeritate dimidia ex ΒΘ, ut tangentes circumferentiae θη, iisdem parallelis inclusae, ad partes rectae Pζ ipsis respondentes. Unde, ut in priori parte demonstrationis, concludetur omnes simul rectae PQ, QΠ &c. hoc est, totam Pζ esse ad omnes simul tangentes θΔ, ΓΣ, &c. sicut tempus quo percurritur tota ΟΩ, cum celeritate dimidia ex ΒΘ, ad tempora omnia motuum quales diximus per tangentes cycloidis SΛ, ΤΞ, &c. Quare & convertendo, tempora omnia per tangentes cycloidis, eam rationem habebunt ad tempus dictum motus aequabilis per rectam ΟΩ, sive per BI, quam dictae tangentes omnes arcus θη ad rectam Pζ vel FG, ac proinde majorem quam arcus LH ad rectam FG; est enim arcus θH, adeoque etiam omnino arcus LH, minor dictis tangentibus arcus θηGa naar margenoot*. Sed tempus per NM posui|mus ab initioGa naar margenoot+ ad idem tempus per BI se habere ut arcus LH ad rectam FG. Ergo tempus per NM, multoque magis tempus per SV, minus erit tempore per tangentes cycloidis. Quod est absurdum, cum hoc tempus, illo per arcum SV, antea minus ostensum fuerit. Patet igitur tempus per arcum cycloidis BE ad tempus per tangentem BI cum celeritate aequabili dimidia ex ΒΘ, non minorem rationem habere quam arcus FH ad rectam FG. Sed nec majorem habere ostensum fuit. Ergo eandem habeat necesse est. quod erat demonstrandum. | |||||||||||||||||||||||||||||||
[pagina 184]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Proposition XXV.Dans une cycloïde à axe vertical et dont le sommet se trouve en bas, les temps de descente dans lesquels un mobile, partant du repos d'un point quelconque de la courbe, atteint le point le plus bas, sont égaux entre eux, et ont au temps de la chute verticale le long de l'axe entier de la cycloïde une raison égale à celle de la demi-circonférence d'un cercle à son diamètre.
Considérons une cycloïde ABC à axe vertical dont le sommet est tourné vers le bas [Fig. 51], et un mobile descendant librement à partir d'un point, tel que B, arbitrairement choisi sur cette courbe, suivant l'arc BA ou suivant une surface possédant la même courbure. Je dis que le temps de la descente de ce mobile est au temps d'une chute le long de l'axe DA, comme la demi-circonférence d'un cercle est à son diamètre. Ceci étant démontré, il sera établi en même temps que les temps de chute le long d'arcs de la cycloïde se terminant en A mais d'ailleurs arbitrairement choisis sont égaux entre eux. Décrivons sur l'axe DA un demi-cercle dont la circonférence soit coupée en E par la droite BF parallèle à la base DC, et après avoir joint les points E et A par une droite, traçons BG parallèle à cette dernière et touchant donc la cycloïde au point B. Supposons que la même droite rencontre en G la droite horizontale tirée par A. Décrivons encore un demi-cercle FHA sur FA. D'après la proposition précédente, le temps de la descente suivant l'arc de cycloïde BA est alors au temps d'un mouvement uniforme le long de la droite BG avec la moitié de la vitesse qui serait acquise par une chute suivant BG, comme le contour FHA du demi-cercle est à la droite FA. Mais le temps du dit mouvement uniforme par BG est égal au temps de la chute libre accélérée suivant la même droite BG, ou à celle suivant EA qui lui est égale et parallèle, c.àd. au temps de la chute accélérée suivant l'axe DAGa naar margenoot*. Par conséquent le temps du mouvement le long de l'arc BA sera | |||||||||||||||||||||||||||||||
[pagina 185]
| |||||||||||||||||||||||||||||||
Propositio XXV.Ga naar margenoot+In Cycloide cujus axis ad perpendiculum erectus est, vertice deorsum spectante, tempora descensus quibus mobile, à quocunque in ea puncto dimissum, ad punctum imum verticis pervenit, sunt inter se aequalia; habentque ad tempus casus perpendicularis per totum axem cycloidis eam rationem, quam semicircumferentia circuli ad diametrum. 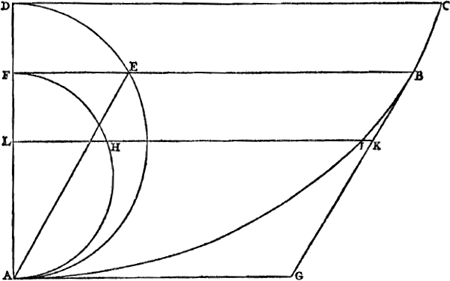 [Fig. 51.]
Esto cyclois ABC [Fig. 51] cujus vertex A deorsum spectet, axis vero AD ad perpendiculum erectus sit, & à puncto quovis in cycloide sumpto, velut B; descendat mobile impetu naturali per arcum BA, sive per superficiem ita inflexam. Dico tempus descensus hujus esse ad tempus casus per axem DA, sicut semicircumferentia circuli ad diametrum. Quo demonstrato, etiam tempora descensus, per quoslibet cycloidis arcus ad A terminatos, inter se aequalia esse constabit. Describatur super axe DA semicirculus, cujus circumferentiam secet recta BF, basi DC parallela, in E; junctâque EA, ducatur ei parallela BG, quae quidem cycloidem tanget in B. Eadem vero occurrat rectae horizontali per A ductae in G: sitque etiam super FA descriptus semicirculus FHA. Est igitur, per praecedentem, tempus descensus per arcum cycloidis BA, ad tempus motus aequabilis per rectam BG cum celeritate dimidia ex BG, sicut arcus semicirculi FHA ad rectam FA. Tempus vero dicti motus aequabilis per BG, aequatur tempori descensus naturaliter accelerati per eandem BG, sive per EA, quae ipsi parallela est & aequalis, hoc est, tempori descensus accelerati per axem DAGa naar margenoot*. Itaque tempus per | |||||||||||||||||||||||||||||||
[pagina 186]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ aussi au temps de chute suivant l'axe DA, comme la circonférence FHA d'un demicercle est à son diamètre FA. C. Q. F. D. Que si l'on suppose la cavité de la cycloïde construite entièrement, il est certain que le mobile, après être descendu le long de l'arc BA, montera, en continuant son mouvement à partir de là, le long du deuxième arc symétrique avec le premierGa naar margenoot* et y employera autant de temps que pour la descenteGa naar margenoot*; et qu'après cela il reviendra de nouveau à B en passant par A et que les temps de ces oscillations cycloïdales d'amplitudes quelconques seront chacun au temps de la chute verticale suivant l'axe DA, comme la circonférence totale du cercle est à son diamètre. | |||||||||||||||||||||||||||||||
Proposition XXVI.Les mêmes choses étant supposées, et une horizontale HI étant en outre tirée [Fig. 51] qui coupe l'arc BA en I et la circonférence FHA en H, je dis que le temps nécessaire pour parcourir l'arc BI est à celui dans lequel est parcouru l'arc IA après BI, comme l'arc FH de la circonférence est à HA.
En effet, supposons que la droite HI coupe la tangente BG en K et l'axe DA en L. Le temps de la chute suivant l'arc BA est alors à celui du mouvement uniforme suivant BG avec la moitié de la vitesse qui proviendrait d'une chute suivant BG, comme l'arc FHA est à la droite FAGa naar margenoot*. Or, le temps du dit mouvement uniforme suivant BG est au temps d'un mouvement uniforme suivant BK avec la même demivitesse, comme la longueur BG est à BK ou comme FA est à FL. D'autre part le temps d'un mouvement uniforme avec la vitesse mentionnée suivant BK est au temps d'une chute suivant BI, comme FL est à l'arc FHGa naar margenoot*. On aura donc ‘ex aequo’Ga naar voetnoot1): le temps d'une chute suivant BA est à celui d'une chute suivant BI comme l'arc FHA est à l'arc FH. Et, par division et conversion: le temps d'une chute le long de BI est à celui d'une chute le long de IA après BI, comme l'arc FH est à l'arc HA. C. Q. F. D. | |||||||||||||||||||||||||||||||
[pagina 187]
| |||||||||||||||||||||||||||||||
arcum BA, erit quoque ad tempus descensus per axem DA, ut semicirculi circumferentiaGa naar margenoot+ FHA ad diametrum FA. quod erat demonstrandum. Quod si tota cycloidis cavitas perfecta ponatur, constat mobile, postquam per arcumGa naar margenoot+ BA descenderit, inde continuato motu per alterum ipsi aequalem arcum ascensurumGa naar margenoot*, atque in eo tantundem temporis atque descendendo consumpturumGa naar margenoot*. Deinde rursus per A ad B perventurum, ac singularum ejusmodi reciprocationum, in magnis parvisve cycloidis arcubus peractarum, tempora fore ad tempus casus perpendicularis per axem DA, sicut circumferentia circuli tota ad diametrum suam.  [Fig. 51.]
| |||||||||||||||||||||||||||||||
Propositio XXVI.Iisdem positis, si ducatur insuper recta horizontalis HI [Fig. 51] quae arcum BA secet in I, circumferentiam vero FHA in H: dico tempus per arcum BI, ad tempus per arcum IA post BI, eam rationem habere quam arcus circumferentiae FH ad HA.
Occurrat enim recta HI tangenti BG in K, axi DA in L. Est itaque tempus per arcum BA, ad tempus motus aequabilis per BG cum celeritate dimidia ex BG, sicut arcus FHA ad rectam FAGa naar margenoot*. Tempus autem dicti motus aequabilis per BG, est ad tempus motus aequabilis per BK, cum eadem celeritate dimidia ex BG, sicut BG ad BK longitudine, hoc est, sicut FA ad FL. Et rursus tempus motus aequabilis, cum dicta celeritate, per BK, ad tempus per arcum BI, sicut FL ad arcum FHGa naar margenoot*. Igitur ex aequoGa naar voetnoot1) erit tempus per arcum BA ad tempus per BI, ut arcus FHA ad FH. Et dividendo, & convertendo, tempus per BI, ad tempus per IA post BI, ut arcus FH ad HA. quod erat demonstrandum. | |||||||||||||||||||||||||||||||
[pagina 188]
| |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
Troisième partie de l'horloge à pendule.
| |||||||||||||||||||||||||||||||
II.Lorsque deux lignes de cette espèce émanent d'un même point et que la convexité de l'une est tournée vers la concavité de l'autre, comme sont placées dans la figure ci-jointe [Fig. 52] les courbes ABC et ADE, elles seront dites concaves l'une et l'autre vers le même côté. | |||||||||||||||||||||||||||||||
III.Si l'on considère un fil, ou une ligne flexible, enroulé sur une ligne courbée vers un seul côté, et que, une extrémité du fil demeurant attachée à la courbe, l'autre en est écartée de telle manière que la partie libre du fil reste toujours tendue, il est manifeste qu'une certaine autre courbe est décrite par cette extrémité du fil. Donnons-lui le nom de Développante. | |||||||||||||||||||||||||||||||
IV.Et que celle sur laquelle le fil est enroulé porte le nom de Développée. Dans la figure qui précède [Fig. 52] ABC est la développée et ADE la développante correspondante de sorte que, lorsque l'extrémité du fil passe de A en D, la partie tendue du fil est la droite DB, le reste BC étant encore enroulé sur la courbe ABC. Il est manifeste que DB touche la développée en B. | |||||||||||||||||||||||||||||||
[pagina 189]
| |||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||
Horologii oscillatorii Pars Tertia.
| |||||||||||||||||||||||||||||||
I.Linea in unam partem inflexa vocetur quam rectae omnes tangentes ab eadem parte contingunt. Si autem portiones quasdam rectas lineas habuerit, hae ipsae productae pro tangentibus habentur. | |||||||||||||||||||||||||||||||
II.Cum autem duae hujusmodi lineae ab eodem puncto egrediuntur, quarum convexitas unius obversa sit ad cavitatem alterius, quales sunt in figura adscripta [Fig. 52] curvae ABC, ADE, ambae in eandem partem cavae dicantur. | |||||||||||||||||||||||||||||||
III.Si lineae, in unam partem cavae, filum seu linea flexilis circumplicata intelligatur, & manente una fili extremitate illi | affixa, altera extremitas abducatur, ita ut pars ea quae soluta est semper extensaGa naar margenoot+ maneat; manifestum est curvam quandam aliam hac fili extremitate describi. Vocetur autem ea, Descripta ex evolutione. | |||||||||||||||||||||||||||||||
IV.Illa vero cui filum circumplicatum erat, dicatur Evoluta. In figura superiori [Fig. 52], ABC est evoluta, ADE descripta ex evolutione ABC, ut nempe cum extremitas fili ex A venit in D, pars fili extensa sit DB recta, reliqua parte BC adhuc applicata curvae ABC. Manifestum est autem DB tangere evolutam in B. | |||||||||||||||||||||||||||||||
[pagina 190]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Proposition IGa naar voetnoot1).Toute tangente à la développée rencontrera la développante à angles droits.
Soit AB [Fig. 53] la développée et AH la ligne décrite par son évolution. Puisse la droite FDC, tangente en D à la courbe AD, couper en C la courbe ACH. Je dis qu'il la coupe à angles droits, en d'autres termes que si l'on mène la droite CE perpendiculairement à CD elle touche la courbe ACH en C. En effet, puisque DC touche la développée en D, il apparaît qu'elle représente la position du fil au moment où son extrémité est parvenue jusqu'au point C; et si nous réussissons à démontrer que le fil, dans la description entière de la courbe ACH, n'atteint nulle part la droite CE excepté au point C, il sera manifeste que la droite CE touche la courbe ACH en ce point. Prenons sur AC un point H quelconque différent de C et considérons d'abord le cas où ce point est plus éloigné de l'origine de la développante que le point C. Supposons que la partie libre du fil soit HG lorsqu'il est parvenu avec son extrémité jusqu'au point H. HG touche donc la ligne AB en G. Et comme dans la description de la partie CH de la courbe, l'arc DG a été développé, CD prolongée du côté D coupera HG, p.e. en F. Appelons E le point de rencontre de GH avec la droite CE. Puisque l'ensemble des deux lignes CF et FG est alors plus grand que DG, que cette dernière soit courbée ou droite, il en résultera, lorsqu'on ajoute de part et d'autre la droite DC, que la somme des droites CF et FG est plus grande que celle de la droite CD et de DG. Mais à cause de l'évolution du fil, il apparaît que la droite HG est égale à la somme de la droite CD et de DG. Par conséquent la somme CF + FG sera aussi plus grande que la droite HG; et en retranchant la partie commune FG, on trouve que CF est plus grande que HF. Or, FE > FC, parce que l'angle C du triangle FCE est droit. FE est donc a fortiori plus grande que FH. D'où il ressort que du moins de ce côté-là du point C l'extrémité du fil n'arrive pas jusqu'à la droite CE. Supposons maintenant le point H plus près de l'origine de la développante que le point C [Fig. 54] et soit HG la position du fil au moment où son extrémité est en H. Tirons les droites DG et DH dont la dernière rencontre la droite CE en E. Il est clair que la droite DG ne peut se trouver sur le prolongement de HG et que HGD sera par conséquent un triangle. Or, comme la droite DG est ou bien plus petite que DKG ou bien son égale, savoir dans le cas ou la partie DG de la développée est droite, on trouvera, en ajoutant GH de part et d'autre, que la somme des droites DG et | |||||||||||||||||||||||||||||||
[pagina 191]
| |||||||||||||||||||||||||||||||
Propositio IGa naar voetnoot1).Ga naar margenoot+Recta omnis, quae evolutam tangit, occurret lineae ex evolutione descriptae ad angulos rectos.  [Fig. 53.]
Sit AB [Fig. 53] evoluta, AH vero quae ex evolutione illius descripta est. Recta autem FDC, tangens curvam AD in D, occurrat in C curvae ACH. Dico ei occurrere ad angulos rectos: hoc est, si ducatur CE recta perpendicularis CD, dico eam in C tangere curvam ACH. Quia enim DC tangit evolutam in D, apparet ipsam referre positionem fili tunc cum ejus extremitas pervenit in C. Quod si igitur ostenderimus filum, in tota reliqua descriptione curvae ACH, nusquam pertingere ad rectam CE praeterquam in C puncto, ma|nifestum erit rectam CEGa naar margenoot+ ibidem curvam ACH contingere. Sumatur punctum aliquod in AC praeter C, quod sit H, sitque primo remotius à principio evolutionis A quam punctum C, & intelligatur pars libera esse HG, cum extremitate sua ad H pervenit. Tangit ergo HG lineam AB in G. Cumque interea dum describitur pars curvae CH, evolutus sit arcus DG, occurret CD à parte D producta ipsi HG, ut in F. Ponatur autem GH occurrere rectae CE in E. Quia igitur duae simul DF, FG, majores sunt quam DG, sive curva ea fuerit sive recta: fiet addendo utrinque rectam DC, ut rectae CF, FG simul majores sint recta CD & ipsa DG. Sed propter evolutionem, apparet utrisque simul, rectae CD, & lineae DG, aequari rectam HG. Ergo duae simul CF, FG majores quoque erunt recta HG; & ablata communi FG, erit CF major quam HF. Sed FE major est quam FC, quia angulus C trianguli FCE est rectus. Ergo FE omnino major quam FH. Unde apparet, ab hac quidem parte puncti C, fili extremitatem non pertingere ad rectam CE. Sit jam punctum H propinquius principio evolutionis A quam punctum C [Fig. 54], sitque fili positio HG, tunc cum ejus extremitas esset in H, & ducantur rectae DG, DH, quarum haec occurrat rectae CE in E: apparet autem DG rectam non posse esse in directum ipsi HG, adeoque HGD fore triangulum. Jam quia recta DG vel minor est quam DKG, vel eadem, si nempe evolutae pars DG recta sit; additâ utrique GH, | |||||||||||||||||||||||||||||||
[pagina 192]
| |||||||||||||||||||||||||||||||
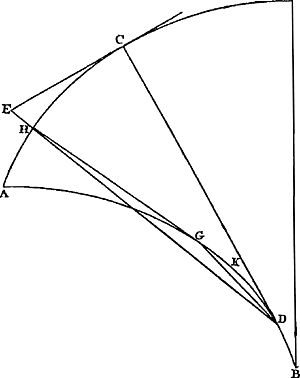 [Fig. 54.]
Ga naar margenoot+ GH est inférieure ou égale à DKG + GH ou bien à la droite DC qui est égale à cette dernière somme. Mais la droite DH est plus petite que la somme des droites DG et GH. DH est donc à plus forte raison inférieure à la droite DC. Or, DE > DC, puisque dans le triangle DCE l'angle C est droit. Par conséquent DH est beaucoup plus petite que DE. Le point H. c.à.d. l'extrémité du fil GH, est donc situé à l'intérieur de l'angle DCE. D'où il appert qu'entre A et C aussi l'extrémité du fil n'arrive nulle part jusqu'à la droite CE. Partant CE touche la courbe AC en C; c'est pourquoi DC, à laquelle CE est perpendiculaire par construction, coupe la courbe à angles droits. C. Q. F. D. Par là il est encore manifeste que AHC est courbée vers un seul côté et qu'elle est concave vers le même côté que AGB, par l'évolution de laquelle elle a été décrite. Car toutes les tangentes à la ligne AHC tombent en dehors de l'espace DGAHC; mais toutes les tangentes à la ligne AGD tombent dans lui. D'où il est évident que la concavité AHC regarde la convexité AGD. | |||||||||||||||||||||||||||||||
Proposition II.Toute ligne courbe terminée, courbée vers un seul côté, telle que ABD [Fig. 55] peut être divisée en un si grand nombre de parties qui si l'on tire les cordes qui soustendent chacun des arcs, telles que AB, BC et CD, et ensuite depuis chacun des points de division et aussi depuis l'extrémité de la courbe les tangentes AN, BO, CP, chacune jusqu'à la normale à la courbe au point de division suivant (BN, CO, DP sont des normales), que chaque corde, dis-je, aura à la normale correspondante (AB à BN, BC à CO, CD à DP) un rapport supérieur à tout rapport arbitrairement donné.
En effet, soit donné le rapport EF : FG [Fig. 55] de deux droites formant les côtés d'un angle droit F et tirons la droite GEH. Supposons d'abord la courbe ABD divisée par les points B, C en des parties si petites que les tangentes à la courbe en deux de ces points qui se suivent se coupent l'une l'autre suivant des angles dont chacun est supérieur à l'angle FEH, tels que ∠ AKB, ∠ BLC et ∠ CMD. La possibilité d'une pareille division est trop évidente | |||||||||||||||||||||||||||||||
[pagina 193]
| |||||||||||||||||||||||||||||||
erunt rectae DG, GH simul minores vel | aequales duabus istis, scilicet DKG & GH,Ga naar margenoot+ sive his aequali rectae DC. Duabus autem rectis DG, GH minor est recta DH. ErgoGa naar margenoot+ haec minor utique erit rectâ DC. Sed DE major est quam DC, quia in triangulo DCE angulus C est rectus. Ergo DH multo minor quam DE. Situm est ergo punctum H, hoc est extremitas fili GH, intra angulum DCE. Unde apparet neque inter A & C usquam illam pertingere ad rectam CE. Ergo CE tangit curvam AC in C; ac proinde DC, cui CE ducta est perpendicularis, occurrit curvae ad angulos rectos. quod erat demonstrandum. Hinc etiam manifestum est curvam AHC in partem unam inflexam esse, & in eandem partem cavam ac ipsa AGB, cujus evolutione descripta est. Omnes enim tangentes lineae AHC, cadunt extra spatium DGAHC: omnes vero tangentes lineae AGD, intra dictum spatium. unde liquet cavitatem AHC respicere convexitatem AGD. | |||||||||||||||||||||||||||||||
Propositio II.Omnis curva linea terminata, in unam partem cava, ut ABD [Fig. 55], potest in tot partes dividi, ut si singulis partibus subtensae rectae ducantur, velut AB, BC, CD; & à singulis item divisionis punctis, ipsaque curvae extremitate rectae ducantur curvam tangentes, ut AN, BO, CP, quae occurrant iis, quae in proxime sequentibus divisionis punctis curvae ad angulos rectos insistunt, quales sunt lineae BN, CO, DP; ut inquam subtensa quaeque habeat ad sibi adjacentem curvae perpendicularem, velut AB ad BN, BC ad CO, CD ad DP, rationem majorem quavis ratione proposita.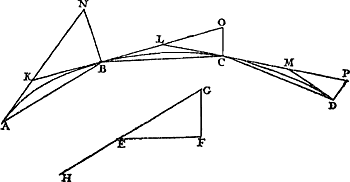
Sit enim data [Fig. 55] ratio lineae EF ad FG, quae recto angulo ad F jungantur, & ducatur recta GEH. Intelligatur primo curva ABD in partes tam exiguas secta punctis B, C, ut tangentes quae ad bina quaeque inter se proxima puncta curvam contingunt, occurrant sibi mutuo secundum angulos qui singuli majores sint angulo FEH; quales sunt anguli AKB, BLC, CMD. quod quidem fieri posse evidentius est quam ut demonstratione | |||||||||||||||||||||||||||||||
[pagina 194]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ pour exiger une démonstration. Les cordes AB, BC et CD ayant été tirées et les normales à la courbe BN, CO, DP ayant été érigées, lesquelles rencontrent les prolongements de AK, de BL et de CM en N, O et P, je dis que chacun des rapports de deux droites AB : BN, BC : CO et CD : CP est supérieur au rapport EF : FG. Car, puisque ∠ AKB > ∠ HEF, ∠ NKB, supplément du premier, sera plus petit que ∠ GEF. Or, l'angle B du triangle KBN est droit, comme F du triangle EFG. Par conséquent KB : BN > EF : FG. Mais AB > KB, puisque l'angle K du triangle AKB est obtus; en effet, il est plus grand que l'angle HEF lequel est obtus par construction. Le rapport AB : BN sera donc plus grand que le rapport KB : BN et à plus forte raison que le rapport EF : FG. On démontrera de la même manière que les rapports BC : CO et CD : DP sont l'un et l'autre plus grands que le rapport EF : FG. La proposition est donc démontrée. | |||||||||||||||||||||||||||||||
Proposition III.Deux lignes courbées l'une et l'autre vers un seul côté et concaves vers le même côté ne peuvent émaner d'un seul point dans une telle position l'une par rapport à l'autre que toute droite normale à l'une soit aussi normale à l'autre.
En effet, soient ACE et AGK possédant l'extrémité commune A, si cela est possible, des lignes courbes de cette espèce [Fig. 56] et soit KE une normale en un point quelconque K de la courbe extérieure à cette dernière: étant normale à cette courbe KE le sera donc aussi à la courbe ACE. Nous pouvons prendre maintenant quelque droite Q plus grande que la courbe KGA. Supposons KGA divisée par les points H, G, F, comme il à été dit dans la proposition précédente, en un si grand nombre de parties que chacune des cordes KH, HG, GF, FA ait à la normale adjacente HM, GN, FO ou AP un rapport supérieur à celui de la ligne Q à la droite KE. L'ensemble des cordes nommées aura donc aussi à la somme de toutes les normales un rapport supérieur à Q : KE. Prolongeons maintenant ces mêmes normales et puissent-elles couper la courbe ACE en D, | |||||||||||||||||||||||||||||||
[pagina 195]
| |||||||||||||||||||||||||||||||
indigeat. Ductis jam subtensis AB, BC, CD, & erectis curvae perpendicularibus BN,Ga naar margenoot+ CO, DP, quae occurrant productis AK, BL, CM, in N, O, P: dico rationes singulas rectarum, AB ad BN, BC ad CO, CD ad DP, majores esse ratione EF ad FG. Quia enim angulus AKB major est angulo HEF, erit residuus illius ad duos rectos,Ga naar margenoot+ nimirum angulus NKB, minor angulo GEF. Angulus autem B trianguli KBN est rectus, sicut & angulus F in triangulo EFG. Ergo major erit ratio KB ad BN quam EF ad FG. Sed AB major est quam KB, quoniam angulus K in triangulo AKB est obtusus, est enim major angulo HEF qui est obtusus ex constructione. Ergo ratio AB ad BN major erit ratione KB ad BN, ac proinde omnino major ratione EF ad FG. Eodem modo & ratio BC ad CO, & CD ad DP, major ostendetur ratione EF ad FG. Itaque constat propositum. | |||||||||||||||||||||||||||||||
Propositio III.Duae curvae in unam partem inflexae & in easdem partes cavae ex eodem puncto egredi nequeunt, ita ad se invicem comparatae, ut recta omnis quae alteri earum ad angulos rectos occurrit, similiter occurrat & reliquae. 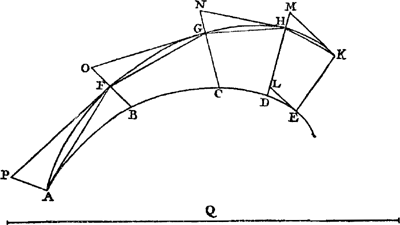 [Fig. 56.]
Sint enim, si sieri potest, hujusmodi lineae curvae ACE, AGK, communem terminum habentes A [Fig. 56], & sumpto in exteriore illarum puncto quolibet K, sit inde educta KE recta, curvae AGK occurrens ad angulos rectos, ac proinde etiam curvae ACE. Potest jam recta quaedam sumi major curva KGA, quae sit Q. Divisa autem intelligaturGa naar margenoot+ ipsa KGA, ut in propositione antecedenti dictum fuit, in tot partes punctis HGF, ut subtensae singulae KH, HG, GF, FA, ad perpendiculares curvae sibi contiguas HM, GN, FO, AP majorem rationem habeant quam linea Q ad rectam KE. Itaque & omnes simul dictae subtensae ad omnes dictas perpendiculares majorem habebunt rationem quam Q ad KE. Producantur autem perpendiculares eaedem & occur- | |||||||||||||||||||||||||||||||
[pagina 196]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ C, et B, normalement par hypothèse. On aura maintenant: KE < MD. En effet, EL, perpendiculaire à KE, sera tangente à la courbe ACE, puisque KE lui est normale; EL coupera donc nécessairement la droite MD entre D et M. Par conséquent KE, qui est la plus courte de toutes les lignes comprises entre les parallèles EL et KM, sera plus petite que ML et à plus forte raison que MD. On démontrera de la même manière que HD < NC, GC < OB, et FB < PA. Comme on a donc PA > FB, la somme PA + OF sera supérieure à OB. Pareillement, puisque OB > GC, la somme OB + NG sera plus grande que NC. Mais la somme PA + OF était supérieure à OB. Par conséquent la somme des trois termes PA, OF et NG sera containement plus grande que NC. Derechef, puisque NC > HD, la somme NC + MH sera plus grande que MD. Partant, si l'on prend au lieu de NC la somme des trois termes PA, OF, NG qui lui est supérieure, la somme des quatre grandeurs PA, OF, NG et MH sera a-fortiori plus grande que MD: et par conséquent cette même somme sera aussi certainement plus grande que la droite KE, puisque MD surpassait KE en longueur. Or, nous avons dit que la somme des soustangentes AF + FG + GH + HK a à celle de toutes les normales PA, OF, NG et MH un rapport supérieur à celui de la ligne Q à KE. Par conséquent la somme de toutes les cordes sera plus grande que la droite Q. Mais cette dernière avait été prise plus grande que la courbe AGK. La somme des cordes AF + FG + CK + HK sera donc plus grande que la courbe AGK aux arcs de laquelle ces cordes correspondent; ce qui est absurde puisque chacune des cordes est plus petite que l'arc correspondant. | |||||||||||||||||||||||||||||||
Proposition IV.Si d'un même point partent deux lignes courbées l'une et l'autre vers un seul côté et concaves vers le même côté, et ainsi situées l'une par rapport à l'autre que toutes les tangentes à l'une d'elles coupent l'autre à angles droits, cette deuxième sera la développante de la première à partir du point commun.
Soient données les lignes ABC et ADE [Fig. 57] courbées l'une et l'autre vers un seul côté et concaves vers le même côté, possédant l'extrémité commune A. Puissent toutes les tangentes à la ligne ABC, telles que BD et CE, couper la ligne ADE normalement. Je dis que ADE est décrite par l'évolution de ABC à partir de l'extrémité A. En effet, supposons, si cela est possible, que par la dite évolution soit décrite une certaine autre courbe AFG. Par conséquent des lignes droites quelconques, tangentes à la développée ABC, telles que BD et CE, couperont cette courbe AFG à angles droitsGa naar margenoot*, p.e. en F et G. Mais par hypothèse ces mêmes tangentes sont aussi normales à la ligne ADE. Or, nous avons affaire à des courbes ADE et AFG, se terminant au même point A, courbées l'une et l'autre vers un seul côté et concaves vers le même | |||||||||||||||||||||||||||||||
[pagina 197]
| |||||||||||||||||||||||||||||||
rant curvae ACE in D, C, B, nimirum ad angulos rectos ex hypothesi. Erit jam KEGa naar margenoot+ minor quam MD. Etenim, ducta EL ipsi KE perpendiculari, quoniam KE occurrit lineae curvae ECA ad angulos rectos, tanget EL curvam ACE, occurretque necessario rectae MD inter D & M. Unde cum KE sit brevissima omnium quae cadunt inter parallelas EL, KM, erit ea minor quam ML, ac proinde minor quoque omnino quam MD. Eodem modo & HD minor ostendetur quam NC, & GC minor quam OB, & FB minor quam PA. Cum sit ergo PA major quam FB, erunt duae simul PA, OF majores quam OB. Item quum OB sit major quam GC, erunt duae simul OB, NG, majores quam NC. Sed duae PA, OF majores erant quam OB. Itaque tres simul PA, OF, NG omnino majores erunt quam NC. Rursus, quia NC major quam HD, erunt duae simul NC, MH majores quam MD. Unde, si loco NC sumantur tres hae ipsa majores PA, OF, NG, erunt omnino hae quatuor PA, OF, NG, MH majores quam MD. ac proinde eaedem quoque omnino majores recta KE, quia ipsa MD major erat quam KE. Diximus autem subtensas omnes AF, FG, GH, HK majorem rationem habere ad omnes perpendiculares PA, OF, NG, MH, quam linea Q ad KE. Ergo cum dictis perpendicularibus minor etiam sit KE, habebunt dictae subtensae ad KE omnino majorem rationem quam Q ad KE. Ergo subtensae simul sumptae majores erunt restâ Q. Haec autem ipsa curvâ AGK major sumpta fuit. Ergo subtensae AF, FG, GH, HK simul majores erunt curva AGK cujus partibus subtenduntur; quod est absurdum, cum singulae suis arcubus sint minores. Non igitur poterunt esse duae curvae lineae quae quemadmodum dictum fuit sese habeant. quod erat demonstrandum. | |||||||||||||||||||||||||||||||
Propositio IV.Si ab eodem puncto duae lineae exeant in partem unam inflexae, & in eandem partem cavae, ita vero mutuo com|paratae ut rectae omnes, quae alteram earum contingunt,Ga naar margenoot+ alteri occurrant ad angulos rectos; posterior haec prioris evolutione, à puncto communi coepta, describetur.
Sunto lineae ABC, ADE [Fig. 57], in partem unam inflexae, & quarum utraque in easdem partes cava existat, habeantque communem terminum A punctum. Omnes autem rectae tangentes lineam ABC, velut BD, CE, occurrant lineae ADE ad angulos rectos. Dico evolutione ipsius ABC, à termino A incepta, describi ADE. Si enim fieri potest, describatur dicta evolutione alia quaedam curva AFG. Ergo lineae rectae quaelibet, evolutam ABC tangentes, ut BD, CE, occurrent ipsi AFG ad angulos rectosGa naar margenoot*, puta in F & G. Sed eaedem tangentes etiam ad rectos angulos occurrere ponuntur lineae ADE. Sunt igitur lineae curvae ADE, AFG, eodem puncto A terminatae, inque partem unam flexae, & ambae in eandem partem cavae, quippe utra- | |||||||||||||||||||||||||||||||
[pagina 198]
| |||||||||||||||||||||||||||||||
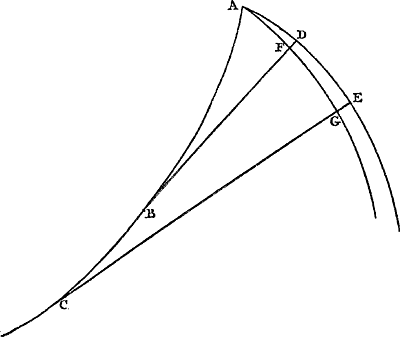 [Fig. 57.]
Ga naar margenoot+ côté, puisqu'elles sont concaves vers le même côté que ABC; car ceci est vrai de la ligne ADE par hypothèse et de la ligne AFG d'après la première proposition de cette Partie. De plus toutes les normales à l'une d'elles sont aussi normales à l'autre. Mais il a été démontré plus haut que ceci est impossibleGa naar margenoot*. Il est donc établi que ADE ellemême sera décrite par l'évolution de la ligne ABC. C. Q. F. D. | |||||||||||||||||||||||||||||||
Proposition V.Lorsqu'une droite touche une cycloïde en son sommet et qu'on construit sur cette droite prise pour base une autre cycloïde, semblable et égale à la première, à partir du point coïncidant avec le sommet nommé, une tangente quelconque à la cycloïde inférieure sera normale à l'arc cycloïdal supérieurGa naar voetnoot1).
Supposons que la droite AG [Fig. 58] touche la cycloïde en son sommet A et que sur cette droite prise pour base une autre cycloïde AEF à sommet F soit construite. Soit BK une tangente à la cycloïde ABC. Je dis que cette tangente, prolongée jusqu'à la cycloïde AEF, la rencontrera à angles droits. En effet, décrivons autour de AD, axe de la cycloïde ABC, le cercle générateur AHD qui coupe BH, parallèle à la base, en H, et tirons la droite HA. Il s'ensuit, puisque BK touche la cycloïde en B, qu'elle est parallèle à la droite HAGa naar margenoot*. Par conséquent AHBK est un parallélogramme et AK est égale à HB, c.à.d. à l'arc AHGa naar margenoot*. Décrivons maintenant le cercle KM égal au cercle générateur AHD, touchant la base AG en K et coupant la droite BK prolongée en E. Comme BKE est parallèle à | |||||||||||||||||||||||||||||||
[pagina 199]
| |||||||||||||||||||||||||||||||
que in eandem atque ipsa ABC; nam de linea ADE constat ex hypothesi, de AFGGa naar margenoot+ vero ex propositione prima hujus; & omnes quae uni earum occurrunt ad angulos rectos, etiam alteri similiter occurrunt. quod quidem fieri non posse antea ostensum estGa naar margenoot*. Quare constat ipsam ADE descrïptum iri evolutione lineae ABC. quod erat demonstrandum. | |||||||||||||||||||||||||||||||
Propositio V.Ga naar margenoot+Si Cycloïdem recta linea in vertice contingat, super qua, tanquam basi, alia cyclois priori similis & aequalis constituatur, initium sumens à puncto dicti verticis; recta quaelibet inferiorem cycloidem tangens, occurret superioris portioni, sibi superpositae, ad angulos rectosGa naar voetnoot1).
Tangat cycloidem ABC in vertice A recta AG [Fig. 58], super qua, tanquam basi, similis aliqua cyclois constituta sit AEF, cujus vertex F. Cycloidem autem ABC tangat recta BK in B. Dico eam productam occurrere cycloidi AEF ad angulos rectos. Describatur enim circa AD, axem cycloidis ABC, circulus genitor AHD, cui occurrat BH, basi parallela, in H, & jungatur HA. Quia ergo BK tangit cycloidem in B, constat eam parallelam esse rectae HAGa naar margenoot*. Itaque AHBK parallelogrammum est, ac proinde AK aequalis HB, hoc est, arcui AHGa naar margenoot*. Sit porro jam descriptus circulus KM, genitori circulo, hoc est ipsi AHD, aequalis, qui tangat basin AG in K, rectam vero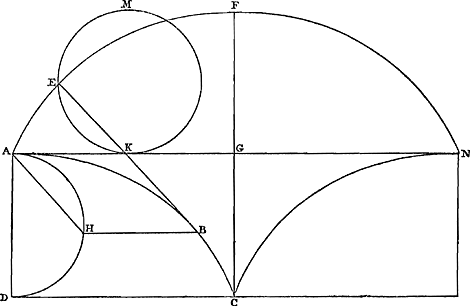
| |||||||||||||||||||||||||||||||
[pagina 200]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ AH et par conséquent EKA = KAH, il est manifeste que le prolongement de BK coupe de la circonférence KM un arc égal à celui que la droite AH coupe de la circonférence AHD. Par conséquent l'arc KE est égal à l'arc AH, c.à.d. à la droite HB et à la droite KA. Mais de cette égalité il résulte, d'après une propriété de la cycloïde, puisque le cercle générateur MK a touché la règle en K, que le point décrivant la cycloïde à passé par E. La droite KE rencontre donc la cycloïde en E à angles droitsGa naar margenoot*. Or, KE n'est autre chose que le prolongement de BK. Il est donc évident que BK prolongée jusqu'à la cycloïde lui est normale. C. Q. F. D. | |||||||||||||||||||||||||||||||
Proposition VI.Par l'évolution, à partir du sommet, d'une demi-cycloïde, une autre demi-cycloïde est décrite, égale et semblable à la première, dont la base coïncide avec la droite qui touche la cycloide développée en son sommet.
Soit donnée une demi-cycloïde ABC [Fig. 58] à laquelle soit imposée une autre demi-cycloïde semblable AEF, comme dans la proposition précédente. Je dis que lorsque la ligne flexible appliquée à la demi-cycloïde ABC est développée à partir du point A, elle décrit de son extrémité la demi-cycloïde AEF. En effet, puisque les demi-cycloïdes ABC et AEF, courbées l'une et l'autre vers un seul côté et concaves vers le même côté, de plus situées de sorte que toutes les tangentes de la demi-cycloïde ABC coupent la demi-cycloïde AEF à angles droits, il s'ensuit que cette dernière est décrite par l'évolution de la première à partir du point AGa naar margenoot*. C. Q. F. D. | |||||||||||||||||||||||||||||||
[pagina 201]
| |||||||||||||||||||||||||||||||
BK productam secet in puncto E. Quia ergo ipsi AH parallela est BKE, ac proindeGa naar margenoot+ angulus EKA aequalis KAH, manifestum est BK productam abscindere à circulo KM arcum aequalem ei quem à circulo AHD abscindit recta AH. Itaque arcus aequalis est arcui AH, hoc est rectae HB, hoc est rectae KA. Hinc | vero sequitur, ex cycloidisGa naar margenoot+ proprietate, cum circulus genitor MK tangebat regulam in K, punctum describens fuisse in E. Itaque recta KE occurrit cycloidi in E ad angulos rectosGa naar margenoot*. Est autem KE ipsa BK producta. Ergo patet productam BK occurrere cycloidi ad angulos rectos. quod erat demonstrandum. | |||||||||||||||||||||||||||||||
Propositio VI.Semicycloidis evolutione, à vertice coepta, alia semicyclois describitur evolutae aequalis & similis, cujus basis est in ea recta quae cycloidem evolutam in vertice contingit.
Sit semicyclois ABC, cui superimposita sit alia similis AEF, quemadmodum in propositione praecedenti [Fig. 58]. Dico si linea flexilis, circa semicycloidem ABC applicata, evolvatur, incipiendo ab A, eam describere extremitate sua ipsam semicycloidem AEF. Quia enim ex puncto A egrediuntur semicycloides ABC, AEF, in unam partem inflexae, & ambae in eandem cavae, ac praeterea ita comparatae, ut omnes tangentes semicycloidis ABC occurrant semicycloidi AEF ad angulos rectos, sequitur hanc evolutione illius, à termino A incepta, describiGa naar margenoot*. quod erat demonstrandum.  [Fig. 58.]
| |||||||||||||||||||||||||||||||
[pagina 202]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Et il apparaît que si nous construisons une demi-cycloïde CN symétrique avec ABC par rapport à la droite CG, une autre demi-cycloïde FN sera décrite par l'extrémité du fil, soit par l'évolution de la courbe CN soit lorsque le fil, déjà tendu suivant CF, est enroulé sur elle; et que cette demi-cycloïde formera avec la précédente, AEF, une cycloïde entière. Par ces considérations, et par la Prop. XXV de la Chute des Corps pesants, la vérité de ce que nous avons dit plus haut dans la Construction de l'Horloge sur le mouvement uniforme du pendule est présentement manifeste. En effet, il est clair que le pendule, suspendu et mis en mouvement entre une paire de lames courbées en forme de demi-cycloïde, décrit par son mouvement un arc de cycloïde et que par conséquent ses oscillations, quelle que soit leur amplitude, sont exécutées dans des temps égaux. Car il n'est d'aucune importance que le mobile parcoure une surface courbée en cycloïde ou bien qu'étant attaché à un fil il décrive cette même ligne en l'air, attendu que dans l'un et l'autre cas il est également libre et a la même inclinaison au mouvement dans tous les points de la courbe. | |||||||||||||||||||||||||||||||
Proposition VII.La cycloïde est quadruple de son axe, en d'autres termes du diamètre du cercle générateur.
En effet d'après la figure précédente reproduite ici [Fig. 58] il apparaît que la demi-cycloïde ABC, égale au fil enroulé sur elle, est double de son axe AD et que par conséquent la cycloïde entière est quadruple de son axe, puisqu'après l'évolution de toute la demi-cycloïde ABC, le fil coïncide avec la droite CF qui est double de AD, attendu que les axes des cycloïdes ABC et AEF sont égaux. Il apparaît aussi que la tangente BE qui n'est autre que la partie tendue du fil d'abord appliquée à l'arc BA, est égale en longueur à ce dernier. Or, BE est le double de BK, ou de AH, puisqu'il a été démontré dans la Proposition V que KE = AH. L'arc cycloïdal AB sera donc le double de la droite AH ou BK, BH étant parallèle à la base de la cycloïde, et cela quel que soit le point B choisi sur elle. Le grand géomètre anglais Christophe Wren a le premier trouvé cette mesure de la cycloïdeGa naar voetnoot1), mais d'une tout autre manière, et il a ensuite confirmé sa proposition par une démonstration élégante qui a été publiée dans le livre sur la cycloïde de Monsieur John WallisGa naar voetnoot2). Il existe en outre sur cette ligne beaucoup de fort belles inventions des mathématiciens de nos jours, auxquelles ont surtout donné occasion certains problèmes proposés par Blaise Pascal, Français qui excellait dans ces études. Celui-ci, faisant le dénombrement tant de ses inventions à lui que de celles des autresGa naar voetnoot3) dit que Mersenne a le premier remarqué l'existence de cette ligne dans la natureGa naar voetnoot4); que | |||||||||||||||||||||||||||||||
[pagina 203]
| |||||||||||||||||||||||||||||||
Et apparet, si dimidiam cycloidem, ipsi ABC gemellam, contrario situ ab alteraGa naar margenoot+ parte lineae CG disponamus, velut CN, ejus evolutione, vel etiam dum filum, jam extensum in CF, circa eam replicatur, alteram semicycloidem FN fili extremitate descriptum iri, quae simul cum priore AEF integram constituat. Atque ex his, & propositione 25 de descensu gravium, manifestum jam est quod supra in Constructione Horologii de aequabili penduli motu dictum fuit. Patet enim perpendiculum, inter laminas binas, secundum semicycloidem inflexas, suspensum agitatumque, motu suo cycloidis arcum describere, ac proinde aequalibus temporibus quaslibet ejus reciprocationes absolvi. Non refert enim utrum in superficie, secundum cycloidem curvata, mobile feratur, an filo alligatum lineam ipsam in aëre percurrrat, cum utrobique eandem libertatem, eandemque in omnibus curvae punctis inclinationem ad motum habeat. | |||||||||||||||||||||||||||||||
Propositio VII.Cyclois linea sui axis, sive diametri circuli genitoris, quadrupla est.
Repetita enim figura praecedenti [Fig. 58]: cum post totam semicycloidem ABCGa naar margenoot+ evolutam, filum occupet rectam CF; quae dupla est AD, propterea quod axes cycloidum ABC, AEF sunt aequales; apparet semicycloidem ipsam ABC, filo sibi circum applicito aequalem, duplam esse sui axis AD, ac totam proinde cycloidem axis sui quadruplam. Apparet etiam tangentem BE, quae refert partem fili extensam, antea curvae parti BA applicatam, huic ipsi longitudine aequari. Est autem BE dupla ipsius BK, sive AH, quoniam in propositione quinta ostensum est KE ipsi AH aequalem esse. Itaque pars cycloidis AB rectae AH, sive BK, dupla erit: existente nimirum BH parallela basi cycloidis: idque ubicunque in ea punctum B sumptum fuerit. Hanc cycloidis dimensionem primus invenit, via tamen longe alia, eximius geometra Christophorus Wren AnglusGa naar voetnoot1), eamque deinde eleganti demonstratione confirmavit, quae edita est in libro de cycloide viri clarissimi Ioannis WallisijGa naar voetnoot2). De eadem vero linea, alia quoque multa extant pulcherrima inventa nostri temporis mathematicorum, quibus praecipuè occasionem praebuere problemata quaedam à Blasio Paschalio Gallo proposita, qui in his studiis praecellebat. Is cum sua, tum aliorum inventa recensensGa naar voetnoot3), primum omnium Mersennum lineam hanc in rerum natura advertisse aitGa naar voetnoot4). Primum | |||||||||||||||||||||||||||||||
[pagina 204]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Roberval a le premier défini ses tangentes et mesuré ses lieux plans et solides; que le même a trouvé les centres de gravité et du plan et de ses parties; que Wren a le premier donné une droite égale à la courbe cycloïdale; que j'ai trouvé, moi le premier, la grandeur absolue de la portion de la cycloïde qui en est coupée par une parallèle à la base passant par un point de l'axe distant du sommet d'un quart de sa longueur, portion égale à la moitié de l'hexagone équilatère inscrit au cercle générateurGa naar voetnoot1); enfin qu'il à déterminé lui-même les centres de gravité des solides et des demi-solides, tant de ceux obtenus par rotation autour de la base qu'autour de l'axe, et de même de leurs parties. Il dit en outre avoir trouvé (mais après avoir reçu de Wren la dimension de la cycloïde) le centre de gravité de la courbe et les dimensions des surfaces convexes dans lesquelles sont comprises les solides mentionnés plus haut et leurs parties, ainsi que les centres de gravité de ces surfaces: et enfin les longueurs des courbes cycloïdales quelconques, tant allongées que raccourcies, c.à.d. de celles qui sont décrites par un point pris à l'intérieur ou à l'extérieur du cercle générateur. Les démonstrations de ces choses ont été publiées par Pascal. Après quoi Monsieur Wallis a aussi exposé ses propres méditations sort subtiles sur la même ligne: il affirme avoir trouvé indépendamment toutes ces mêmes propriétés et avoir résolu les problèmes proposés par Pascal. Le très savant Lovera s'attribue la même choseGa naar voetnoot2). Que les savants jugent, d'après leurs écrits, combien est dû à chacun d'eux. Pour nous, nous avons rapporté ce qui précède puisqu'il nous semblait que nous ne devions pas passer sous silence des inventions si belles par lesquelles il est arrivé que de toutes les lignes aucune n'est maintenant connue mieux et plus à fond que la cycloïde. Quant à notre méthode de | |||||||||||||||||||||||||||||||
[pagina 205]
| |||||||||||||||||||||||||||||||
Robervallium tangentes ejus defini|visse, ac plana & solida dimensum esse. Item centraGa naar margenoot+ gravitatis tum plani, tum partium ejus invenisse. Primum Wrennium curvae cycloidisGa naar margenoot+ aequalem rectam dedisse. Me quoque primum reperisse dimensionem absolutam portionis cycloidis, quae rectâ, basi parallelâ, abscinditur per punctum axis, quod quarta parte ejus à vertice abest. quae nimirum portio aequatur dimidio hexagono aequilatero, intra circulum genitorem descriptoGa naar voetnoot1). Seipsum denique solidorum ac semisolidorum, tam circa basin quàm circa axem, centra gravitatis definivisse, itemque partium eorum. Lineae etiam ipsius (Sed haec post acceptam à Wrennio dimensionem) centrum gravitatis invenisse, & dimensionem superficierum convexarum, quibus solida ista eorumque partes comprehenduntur; earumque superficierum centra gravitatis. Ac denique dimensionem curvarum cujusvis cycloidis, tam protractae quam contractae: hoc est earum quae describuntur à puncto intra vel extra circumferentiam circuli genitoris sumpto. Et horum quidem demonstrationes à Paschalio sunt editae. A quibus suas quoque, de eadem linea, subtilissimas meditationes exposuit Cl. Wallisius, atque eadem illa omnia suo Marte se reperisse, ac problemata à Paschalio proposita solvisse contendit. Quod idem & doctissimus Lovera sibi vindicatGa naar voetnoot2). Quantum vero unicuique debeatur, ex scriptis eorum eruditi dijudicent. Nos propterea tantum praecedentia retulimus, quod silentio praetereunda non videbantur egregia adeo inventa, quibus factum est, ut, ex lineis omnibus, nulla nunc melius aut penitius quam cyclois cognita sit. Methodum

| |||||||||||||||||||||||||||||||
[pagina 206]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ la mesurer, il nous a semblé devoir l'appliquer aussi à d'autres lignes: c'est de quoi nous traiterons maintenant. | |||||||||||||||||||||||||||||||
Proposition VIII.Montrer quelle est la ligne par l'évolution de laquelle la parabole est décriteGa naar voetnoot1).
Soit une paraboloïde AB à axe AD et sommet A [Fig. 59] ayant cette propriété que, BD étant normale à l'axe, le cube de DA, abscisse correspondant au sommet, est égal au solide qui a pour base le carré de DB et pour hauteur une droite donnée M. Cette courbe est connue depuis longtemps aux géomètres. Prolongeons l'axe DE d'une longueur AE = 8/27 M. Si l'on applique maintenant un fil continu à EAB et que celui-ci est développé à partir du point E, je dis que la développante est la parabole EF à axe EAG et sommet E et dont le latus rectum est égal au double de EA. En effet, après avoir pris sur la courbe AB un point quelconque B, menons-y la tangente BG coupant l'axe EA en G. Tirons ensuite à partir de ce point G la droite GF normale à la parabole EF en F. Soit FH une perpendiculaire à GF, donc une tangente à la parabole en F, et enfin FK une normale à l'axe. KG est donc égale à la moitié du latus rectum, c.à.d. à EA, par conséquent, en ajoutant ou retranchant AK de part et d'autre, on trouve que EK = AG. Or, AG est le tiers de AD puisque BG touche la paraboloïde en B: c'est ce qu'on peut aisément démontrer d'après la nature de cette courbe. Il s'ensuit que EK elle aussi est égale au tiers de AD; et KH qui d'après la nature de la parabole est le double de KE sera égale aux deux tiers de AD. Par conséquent le cube de KH est égal à 8/27 fois le cube de AD, c.à.d. au solide ayant pour base le carré de DB et pour hauteur 8/27 M, c.à.d. AE. C'est pourquoi, comme DB2 est à KH2, ainsi sera KH à AE, c.à.d. à KG. Mais nous avions: KH = ⅔ AD = GD. Comme BD2 est à DG2, ainsi est donc HK à KG. D'autre part, comme HK est à KG, ainsi est FK2 à KG2. Par conséquent, comme | |||||||||||||||||||||||||||||||
[pagina 207]
| |||||||||||||||||||||||||||||||
vero nostram, qua in hac metienda usi sumus, in aliis quoque experiri libuit, de quibusGa naar margenoot+ porro nunc agemus. | |||||||||||||||||||||||||||||||
Propositio VIII.Cujus lineae evolutione parabola describatur ostendereGa naar voetnoot1). 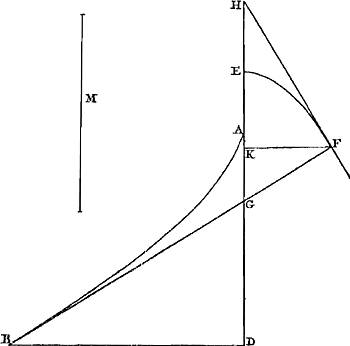 [Fig. 59.]
Sit paraboloides AB, cujus axis AD; vertex A [Fig. 59]; proprietas autem ista, ut ordinatim ad axem applicatâ BD, cubus abscissae ad verticem DA aequetur solido, basin habenti quadratum DB, altitudinem vero aequalem lineae cuidam datae M; quae quidem curva pridem geometris nota fuit; & ponatur axi DE juncta in directum AE, quae habeat 8/27 ipsius M. Jam si filum continuum circa EAB applicetur, idque ab E evolvi incipiat, dico descri|ptam ex evolutioneGa naar margenoot+ esse parabolam EF, cujus axis EAG, vertex E, latus rectum aequale duplae EA. Sumpto enim in curva AB puncto quolibet B, ducatur quae in ipso tangat curvam recta BG, occurrens axi EA in G. & ex G ducatur porro GF, quae ad rectos angulos occurrat parabolae EF in F; & sit ipsi GF perpendicularis FH, quae parabolam in F continget; & denique FK ordinatim ad axem EG applicetur. Est igitur KG aequalis dimidio lateri recto, hoc est, ipsi EA; ac proinde, additâ vel ablatâ utrimque AK, erit EK aequalis AG. Est autem AG triens ipsius AD, quoniam BG tangit paraboloidem in B: illud enim ex natura curvae hujus facile demonstrari potest. Ergo & EK aequalis est trienti AD: & KH, quae ex natura parabolae dupla est KE, aequabitur duabas tertiis AD. Itaque cubus ex KH aequalis est 8/27 cubi ex AD, hoc est, solido basin habenti quadratum DB, altitudinem vero aequalem 9/27 M, hoc est, ipsi AE. Quamobrem ut quadratum DB ad quadratum KH, ita erit KH longitudine ad AE, hoc est ad KG. Erat autem KH aequalis ⅔ AD, hoc est ipsi GD. Ergo ut quadratum BD ad quadratum DG ita est HK ad KG. Ut autem HK ad KG, ita est quadratum FK ad quadratum KG. Ergo sicut quadratum BD ad quadratum | |||||||||||||||||||||||||||||||
[pagina 208]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ BD2 est à DG2 ainsi est FK2 à KG2. Donc BD : DG = FK : KG. Il s'ensuit que BGF est une ligne droite. Mais GF est normale à la parabole EF. Il paraît donc que BG, tangente à la paraboloïde, rencontre, lorsqu'on la prolonge, la parabole à angles droits. Et ceci sera démontré de la même manière de n'importe quelle tangente à la même courbe. Il est donc établi que la parabole EF est décrite par l'évolution de la ligne EAB depuis son extrémité EGa naar margenoot*. C. Q. F. D. | |||||||||||||||||||||||||||||||
Proposition IX.Trouver une ligne droite égale à un arc donné d'une paraboloide, savoir de celle pour laquelle les carrés des ordonnées sont entre eux comme les cubes des abscisses.
Il est évident par la proposition précédente comment ceci doit être fait. Toutefois point n'est besoin de la parabole EF [Fig. 59] pour cette construction qui sera exécutée comme suit. Etant donnée une partie quelconque AB [Fig. 60] de cette paraboloïde, à laquelle il s'agit d'égaler une droite, soit tirée BG tangente au point B et rencontrant l'axe AG en G. Or, BG sera en effet une tangente lorsque AG est le tiers de AD laquelle est comprise entre le sommet et l'ordonnée BD. Après avoir pris ensuite AE = 8/27 M, M étant le latus rectum de la paraboloïde AB, tirons EF // BG et puisse-t-elle couper la ligne AF, parallèle à BD, en F. Si l'on ajoute maintenant à la droite BG la différence NF dont la droite EF surpasse EA, on aura une droite égale à la courbe AB. De quoi la démonstration se voit aisément par les choses auparavant dites. La courbe AB surpasse donc toujours la tangente BG d'une longueur égale à celle donc la droite EF surpasse la droite EA. Or, ici nous sommes tombés de nouveau sur une ligne dont d'autres ont mesuré la longueur avant nous. C'est la ligne que Jean van Heuraet de Harlem a en 1659 montré être égale à une droite; sa démonstration a été ajoutée aux commentaires de Jean van Schooten sur la Géométrie de Descartes publiés la même année. Van Heuraet a donc, le premier de tous, rectifié une courbe du nombre de celles dont des points quelconques sont définis géométriqument, après que peu auparavant Wren avait rectifié la cycloïde par un épichérème non moins ingénieux. | |||||||||||||||||||||||||||||||
[pagina 209]
| |||||||||||||||||||||||||||||||
DG, ita quadratum FK ad quadratum KG. Et proinde sicut BD ad DG longitudine,Ga naar margenoot+ ita FK ad KG. Unde sequitur BGF esse lineam rectam. Sed GF occurrit parabolae EF ad angulos rectos. Ergo apparet BG, tangentem paraboloidis, productam occurrere eidem parabolae ad | angulos rectos. Idque similiter de quavis illius tangente demonstrabitur.Ga naar margenoot+ Ergo constat ex evolutione lineae EAB, à termino E incepta, describi parabolam EFGa naar margenoot*. quod erat demonstandum. | |||||||||||||||||||||||||||||||
Propositio IX.Rectam lineam invenire aequalem datae portioni curvae paraboloidis, ejus nempe in qua quadrata ordinatim applicatarum ad axem, sunt inter se sicut cubi abscissarum ad verticem. 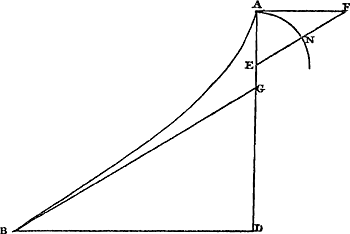 [Fig. 60.]
Quomodo hoc fiat ex prop. praecedenti manifestum est. Parabola vero EF [Fig. 59] ad constructionem non requiritur, quae sic peragetur. Data quavis parte paraboloidis hujus AB [Fig. 60] cui rectam aequalem invenire oporteat, ducatur BG tangens in puncto B, quae occurrat axi AG in G. Tanget autem si AG fuerit tertia pars AD, inter verticem & ordinatim applicatam BD interceptae. Porro sumpta AE aequali 8/27 lineae M, quae latus rectum est paraboloidis AB, ducatur EF parallela BG, occurratque lineae AF, quae parallela est BD, in F. Jam si ad rectam BG addatur NF, excessus rectae EF supra EA, habebitur recta aequalis curvae AB. Cujus demonstratio ex ante dictis facile perspicitur. Semper ergo curva AB tantum superat tangentem BG, quantum recta EF rectam EA. Rursus autem hic in lineam incidimus, cujus longitudinem alii jam ante dimensi sunt. Illam nempe quam anno 1659 Joh. Heuratius Harlemensis rectae aequalem ostendit, cujus demonstratio post commentarios Joh. Schotenii in Cartesii Geometriam, eodem anno editam, adjecta est. Et ille quidem omnium primus curvam lineam, ex earum numero quarum puncta quaelibet geo|metricè definiuntur, ad hanc mensuramGa naar margenoot+ reduxit, cum sub idem tempus Cycloidis longitudinem dedisset Wrennius, non minus ingenio soepicheremate. | |||||||||||||||||||||||||||||||
[pagina 210]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Je sais il est vrai qu'après la publication de la découverte de van Heuraet, le très savant Wallis, dans son livre de la cissoïde, a voulu l'attribuer aussi à Guillaume Neile, gentilhomme de son pays. Mais à mon avis, quand je considère ce qu'il avance dans ce livre, Neile n'a pas à vrai dire été beaucoup éloigné de cette trouvaille sans toutefois y parvenir tout-à-fait. Car d'après sa démonstration même rapportée par Wallis il apparaît qu'il ne comprenait pas clairement quelle serait cette courbe dont il voyait que, si elle était construite, la mesure seraît donnée. Et il est croyable que s'il avait su qu'il s'agit d'une courbe du nombre de celles qui étaient connues depuis longtemps aux géomètres, lui-même, ou d'autres en son nom, leur auraient communiqué un esi noble invention sous une forme plus achevée; invention qui méritait autant ou plus que toute autre qu'ils s'écriassent εὕπηϰα comme jadis Archimède. Sans doute Fermat, conseiller de Toulouse et très habile géomètre, a rédigé de la même invention des preuves qui ont été imprimées en 1660, mais celles-ci datent apparemment de plus tardGa naar voetnoot1). Or, puisque nous sommes engagés dans ce sujet, qu'il nous soit permis de dire aussi ce que nous avons contribué à l'avancement d'une si excellente découverte: nous avons donné à van Heuraet l'occasion d'y parvenir et nous avons trouvé avant lui et les premiers de tous la dimension de la courbe parabolique d'après la quadrature, supposée donnée, de l'hyperbole, ce qui fait partie de la trouvaille de van Heuraet. En effet, vers la fin de l'année 1657 nous sommes tombés simultanément sur ces deux choses, la dimension mentionnée de la courbe parabolique et la réduction de la surface du conoïde parabolique au cercle. Et comme nous avions fait savoir par une lettre à van Schooten, et à d'autres de nos amis, que deux découvertes extraordinaires au au sujet de la parabole nous étaient venues dans l'esprit et que l'une d'elles était la réduction de la surface du conoïde parabolique à un cercle, v. Schooten communiqua cette lettre à van Heuraet qui était alors son ami intime. Il ne fut pas difficile à cet homme, doué d'un esprit fort pénétrant, de comprendre que la dimension de la courbe parabolique elle-même était dans un étroit rapport avec celle de la surface du conoïde. Ayant trouvé l'une et l'autre et poussant ses recherches encore plus loin il tomba sur ces autres courbes paraboloïdales, auxquelles on trouve des droites absolument égalesGa naar voetnoot2). Et afin que nul ne désire, comme cela pourrait avoir lieu, de témoignage sur la réduction de la surface du conoïde à une surface plane, il me semble bon de citer ici une lettre de Monsieur François Slusius qu'il faut considérer comme un des principaux géomètres d'aujourd'hui: dans cette lettre, datant de la même année, il me félicitait de cette découverte, peut-être plus expressément que je ne méritais. Voici une citation de sa lettre du 24 décembre de l'année 1657Ga naar voetnoot3): ‘J'ajoute seulement deux choses, l'une etc. L'autre que je ne compte presque pour rien toutes ces courbes et même | |||||||||||||||||||||||||||||||
[pagina 211]
| |||||||||||||||||||||||||||||||
Scio equidem, ab edito Heuratii invento, Doctissimum Wallisium Wilhelmo Nelio,Ga naar margenoot+ nobili apud suos juveni, idem attribuere voluisse, in libro de Cissoide. Sed mihi, quae illic adfert perpendenti, videtur non multum quidem ab invento illo Nelium abfuisse, neque tamen plane id adsecutum esse. Nam neque ex demonstratione ejus, quam Wallisius affert, apparet illum satis perspexisse quaenam foret curva illa, cujus, si construeretur, mensuram datam fore videbat. Et credibile est, si scivisset ex earum numero esse quae jampridem Geometris cognitae fuerant, vel ipsum, vel alios ejus nomine, tam nobile inventum Geometris maturius impertituros fuisse, quod, si quod aliud, merebatur ut Archimedeum illud εὕρηϰα exclamarent. Sane ejusdem inventi, tanquam à se profecti, etiam Fermatius, Tholosanus senator ac Geometra peritissimus, demonstrationes conscripsit, quae anno 1660 excusae sunt, sed illae sero utiqueGa naar voetnoot1). Cum vero in his simus, etiam de nobis dicere liceat, quid ad promovendum tam eximium inventum contulerimus: siquidem & Heuratio ut eo perveniret occasionem praebuimus, & dimensionem curvae parabolicae ex hyperbolae data quadrature, quae Heuratiani inventi pars est, ante ipsum atque omnium primi reperimus. Etenim sub finem anni 1657 in haec duo simul incidimus, curvae parabolicae quam dixi dimensionem, & superficiei conoidis parabolici in circulum reductionem. Cumque Schotenio, aliisque item amicorum, per literas indicassemus, duo quaedam non vulgaria circa parabolam inventa nobis sese obtulisse, eorumque alteram esse conoidicae superficiei extensionem in circulum, ille literas eas cum Heuratio, quo tum familiariter utebatur, communicavit. Huic vero, acutissimi ingenii viro, non difficile fuit intelligere, conoidis istius superficiei affinem esse dimensionem ipsius curvae parabolicae. Qua utraque inventa, ulterius inde investigans, in alias istas curvas paraboloides incidit, quibus rectae aequales absolute inveniunturGa naar voetnoot2). Ac de Conoidis quidem superficie in planum redacta, ne quis forte testimonium desideret, pauca haec adscribere visum est ex literis viri clarissimi, atque inter praecipuos hodie Geometras censendi, Franc. Slusii, quibus eo ipso anno mihi inventum illud, ac prolixius forte quam pro merito, gratulatus est. In quibus literis | 24. Decemb. anniGa naar margenoot+ 1657.Ga naar voetnoot3) datis, ista habentur. Duo tantum addo, unum &c. Alterum est, me has om- | |||||||||||||||||||||||||||||||
[pagina 212]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ le lieu linéaire entier en comparaison avec votre découverte d'une démonstration de l'existence d'un rapport déterminé entre la surface du conoïde parabolique et le cercle qui en est la base. Je donne volontiers la préférence à cette belle induction pour la quadrature du cercle à toutes les diverses choses que j'ai tirées autrefois du lieu linéaire et que je vous communiquerai à l'occasion si vous le désirez’. L'année suivante je trouvai aussi les surfaces des conoïdes hyperboliques et sphéroïdaux, c.à.d. leur réduction à des cercles, et je fis connaître les constructions de ces problèmes, sans toutefois y ajouter de démonstration, aux géomètres avec qui j'étais alors en commerce de lettres, savoir Pascal et autres en France et Wallis en Angleterre. Ce dernier publia peu après ses idées à lui sur ces sujets ensemble avec beaucoup d'autres inventions subtiles, ce qui fut cause que je ne travaillai pas tout de suite à l'achèvement de mes démonstrationsGa naar voetnoot1). Mais puisque mes constructions ne me paraissent pas manquer d'élégance et qu'elles sont encore inédites, je veux les insérer ici. | |||||||||||||||||||||||||||||||
Trouver un cercle égal à la surface courbe d'un conoïde paraboliqueGa naar voetnoot2).Soit donné un conoïde [Fig. 61] dont la parabole ABC soit la section par l'axe; que BD soit l'axe du conoïde, B son sommet, AC le diamètre de sa base, lequel est perpendiculaire à l'axe. Et soit demandé de trouver un cercle égal à la surface courbe du conoïde. Qu'on prenne, après avoir prolongé l'axe du côté du sommet, BE = BD et qu'on tire EA, tangente en A à la parabole ABC. Que l'on coupe ensuite AD en G de telle manière que AG : GD = EA : AD. Soit H une droite égale à AE + DG et L une droite égale au tiers de la base AC. Soit K la moyenne proportionnelle que l'on peut construire entre H et L. Décrivons un cercle de rayon K. Celui-ci sera égal en surface à la surface courbe ABC du conoïde. Il s'ensuit que si AE = 2AD la surface courbe du conoïde sera au cercle qui en forme la base comme 14 est à 9; si AE = 3AD, comme 13 est à 6; si AE = 4AD, comme 14 est à 5. Et qu'ainsi ce rapport sera toujours exprimé par celui de deux nombres entiers, lorsqu'il en est de même pour celui de AE à AD. | |||||||||||||||||||||||||||||||
Trouver un cercle égal à la surface d'un sphéroïde allongéGa naar voetnoot3).Considérons un sphéroïde oblong [Fig. 62] d'axe AB et de centre C. Soit ABDE une ellipse obtenue par la section du sphéroïde par l'axe, et DE son petit diamètre. | |||||||||||||||||||||||||||||||
[pagina 213]
| |||||||||||||||||||||||||||||||
nes curvas, ipsumque adeo locum linearum integrum, nihili pene facere prae inventoGa naar margenoot+ hoc tuo, quo superficiei in conoide parabolico rationem ad circulum suae baseos demonstrasti. Hanc pro circuli quadratura pulcherrimam ἀπαγωγὴν praefero libens iis omnibus, quas ex loco lineari nec paucas olim deduxi, & quas tecum, si ita jusseris, data occasione communicabo. Anno autem insequenti etiam superficies conoidum hyperbolicorum & sphaeroidum reperi, quomodo ad circulos reduci possent, constructionesque eorum problematum, non addita tamen demonstratione, Geometris quibuscum tunc literarum commercium habebam, in Gallia Paschalio aliisque, in Anglia Wallisio impertii, qui non multo post sua quoque super his, una cum aliis multis subtilibus inventis in lucem edidit, fecitque ut nostris demonstrationibus perficiendis supersederem. Quoniam vero non inelegantes visae sunt constructiones nostrae, neque adhuc publice extant, placet hoc loco illas adscribere. | |||||||||||||||||||||||||||||||
Conoidis parabolici superficiei curvae circulum aequalem invenireGa naar voetnoot2). [Fig. 61.]
Sit datum conoides [Fig. 61] cujus sectio per axem parabola ABC; axis ejus BD, vertex B, diameter basis AC, quae sit axi BD ad angulos rectos. Et oporteat superficiei portionis curvae invenire circulum aequalem. Producto axe à parte verticis, sumaturGa naar margenoot+ BE aequalis BD, & jungatur EA, quae parabolam ABC in A continget. Porro secetur AD in G, ut sit AG ad GD sicut EA ad AD. Et utrisque simul AE, DG aequalis statuatur recta H. Item trienti basis AC aequalis sit recta L, & inter H & L media proportionalis inveniatur K. qua tanquam radio circulus describatur. Is aequalis erit superficiei curvae conoidis ABC. Hinc sequitur, si fuerit AE dupla AD, superficiem conoidis curvam ad circulum baseos fore ut 14 ad 9. Si AE tripla AD, ut 13 ad 6. si AE quadrupla AD, ut 14 ad 5. Atque ita semper fore ut numerus ad numerum, si AE ad AD ejusmodi rationem habuerit. | |||||||||||||||||||||||||||||||
Sphaeroidis oblongi superficiei circulum aequalem invenireGa naar voetnoot3).Esto sphaeroides oblongum [Fig. 62] cujus axis AB, centrum C, sectio per axem ellipsis ADBE, cujus minor diameter DE. | |||||||||||||||||||||||||||||||
[pagina 214]
| |||||||||||||||||||||||||||||||
 [Fig. 62.]
Ga naar margenoot+ Posons DF = CB, en d'autres termes soit F un des deux foyers de l'ellipse ADBE; et tirons la droite BG parallèle à FD, laquelle rencontre le prolongement de ED en G. Décrivons maintenant sur l'axe AB du centre G, avec le rayon GB, l'arc de circonférence BHA. Et soit la droite K moyenne proportionnelle entre le demi-diamètre CD et une droite égale à la somme de l'arc AHB et du diamètre DE. Cette droite K sera le rayon d'un cercle égal à la surface du sphéroïde ADBE. | |||||||||||||||||||||||||||||||
Trouver un cercle égal à la surface du sphéroïde large ou aplatiGa naar voetnoot1). [Fig. 63.]
Considérons un sphéroïde aplati d'axe AB et de centre C [Fig. 63]. Soit ADBE une ellipse obtenue par la section du sphéroïde par l'axe. Soit de nouveau F l'un des deux foyers et, après avoir divisé FC en G, supposons construite une parabole AGB ayant AB pour base et le point G pour sommet. Et soit H une moyenne proportionnelle entre le diamètre DE et une droite égale à la courbe parabolique AGB. Cette droite H sera le rayon d'un cercle égal à la surface du sphéroïde considéré. | |||||||||||||||||||||||||||||||
Trouver un cercle égal à la surface courbe d'un conoïde hyperboliqueGa naar voetnoot2).Soit donné un conoïde hyperbolique à axe AB [Fig. 64] et dont la section par l'axe soit l'hyperbole CAD à latus transversum EA, à centre F et à latus rectum AG. Prenons sur l'axe la droite AH égale à la motié du latus rectum AG. Et comme | |||||||||||||||||||||||||||||||
[pagina 215]
| |||||||||||||||||||||||||||||||
Ponatur DF aequalis CB, seu ponatur F alter focorum ellipseos ADBE rectaequeGa naar margenoot+ FD parallela ducatur BG, occurrens productae ED in G, centroque G, radio GB, describatur super axe AB arcus circumferentiae BHA. Interque semidiametrum CD & rectam utrisque aequalem, arcui AHB & diametro DE, media proportionalis sit recta K. Erit haec radius circuli qui superficiei sphaeroidis ADBE aequalis sit. | |||||||||||||||||||||||||||||||
Sphaeroidis lati sive compressi superficiei circulum aequalem invenireGa naar voetnoot1).Ga naar margenoot+Sit sphaeroides latum cujus axis AB, centrum C [Fig. 63], sectio per axem ellipsis ADBE. Sit rursus focorum alteruter F, divisâque bifariam FC in G, intelligatur parabola AGB quae basin habeat axem AB, verticem vero punctum G. Sitque inter diametrum DE, & rectam curvae parabolicae AGB aequalem, media proportionalis linea H. Erit haec radius circuli qui superficiei sphaeroidis propositi aequalis sit. | |||||||||||||||||||||||||||||||
Conoidis hyperbolici superficiei curvae circulum aequalem invenireGa naar voetnoot2).Esto conoides hyperbolicum [Fig. 64] cujus axis AB, sectio per axem hyperbola CAD, cujus latus transversum EA, centrum F, latus rectum AG. Sumatur in axe recta AH, aequalis dimidio lateri recto AG, & ut HF ad AF longi-
| |||||||||||||||||||||||||||||||
[pagina 216]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ HF est à AF en longueur, ainsi soit AF à FK en puissance. Supposons construite une autre hyperbole KLM à sommet K, qui possède le même axe et le même centre F et qui ait son latus rectum et son latus transversum inversement proportionnels aux grandeurs correspondantes de la première. Que BC prolongée la coupe en M et que AL soit parallèle à BC. La surface courbe du conoïde sera maintenant au cercle de diamètre CD qui constitue sa base, comme l'espace ALMB, compris entre trois droites et la courbe hyperbolique, est à la moitié du carré de BC. On achèvera donc aisément la construction, posée la quadrature de l'hyperbole.
Tandis que d'après notre démonstration la surface du conoïde parabolique se réduit, tout aussi bien que celle de la sphère, à la surface d'un cercle suivant les règles connues de la géométrie, il faut admettre, pour que cette reduction ait lieu pour la surface du sphéroïde allongé, que la longueur d'un arc de circonférence puisse être égalée à une droite. Mais la quadrature de l'hyperbole est requise pour la complanation correspondante de la surface du sphéroïde aplati, ainsi que pour celle de la surface du conoïde hyperbolique. Car la longueur de la ligne parabolique, que nous avons employée dans le cas de ce sphéroïde, dépend de la quadrature de l'hyperbole, comme nous le montrerons tout-à-l'heure. Cependant nous avons trouvé, ce qui ne semble pas indigne d'être remarqué, qu'on peut construire, sans supposer aucunement la quadrature de l'hyperbole, un cercle égal à la somme des surfaces d'un sphéroïde aplati et d'un conoïde hyperbolique. En effet, nous avons réussi à prouver qu'étant donné un sphéroïde aplati quelconque, on peut trouver un conoïde hyperbolique, ou au contraire qu'étant donné un conoïde hyperbolique, on peut trouver un sphéroïde aplati tel qu'il est possible d'obtenir un cercle égal à la somme des surfaces des deux corpsGa naar voetnoot1). Il suffira d'en avoir donné un seul exemple dans un cas plus simple que les autres. Soit donné un sphéroïde aplati à axe SI [Fig. 65] et que STIK soit une ellipse obtenue par une section du sphéroïde par l'axe. Soit O le centre de cette ellipse et TK son grand axe. Que la forme de l'ellipse soit telle que son latus transversum TK ait à son latus rectum un rapport égal à celui d'une ligne divisée en extrême et moyenne raison à sa plus grande partie. Prenons BC double en puissance à SO et de même BA double en puissance par rapport à OK. Que BC, BA, BF et BE soient en proportion continue et que EP soit prise égale à EA. Supposons maintenant construit un conoïde hyperbolique QFN à | |||||||||||||||||||||||||||||||
[pagina 217]
| |||||||||||||||||||||||||||||||
tudine, ita sit AF ad FK potentiâ. Et intelligatur vertice K alia hyperbola descriptaGa naar margenoot+ KLM, eodem axe & centro F cum priore, quaeque latera rectum & transversum illi reciproce proportionalia habeat. Occurrat autem ipsi producta BC in M, sitque AL parallela BC. Erit jam sicut spatium ALMB, tribus rectis lineis & curva hyperbolica comprehensum, ad dimidium quadratum ex BC, ita superficie conoidis curva ad circulum baseos suae, cujus diameter CD. Unde constructio reliqua sacile absolvetur, positâ hyperbolae quadraturâ. Quum igitur conoidis parabolici superficies ad circulum redigatur, aeque ac superficies sphaerae, ex notis geometriae regulis; in superficie sphaeroidis oblongi, ut idem fiat, ponendum est arcus | circumferentiae longitudinem aequari posse lineae rectae. AdGa naar margenoot+ sphaeroidis vero lati, itemque ad conoidis hyperbolici superficiem eadem ratione complanandam, hyperbolae quadratura requiritur. Nam parabolicae lineae longitudo, quam in sphaeroide hoc adhibuimus, pendet à quadratura hyperbolae, ut mox ostendemus. Verum, quod non indignum animadversione videtur, invenimus absque ulla hyperbolicae quadraturae suppositione, circulum aequalem construi superficiei utrique simul, sphaeroidis lati & conoidis hyperbolici. Dato enim sphaeroide quovis lato, posse inveniri conoides hyperbolicum, vel contra, dato conoide hyperbolico, posse inveniri sphaeroides latum ejusmodi, ut utriusque simul superficiei exhibeatur circulus aequalisGa naar voetnoot1). cujus exemplum in casu uno caeteris simpliciore sufficiet attulisse. Sit sphaeroides latum cujus axis SI [Fig. 65], sectio per axem ellipsis STIK, cujus ellipsis centrum O, axis major TK. ponatur autem ellipsis haec ejusmodi, ut latus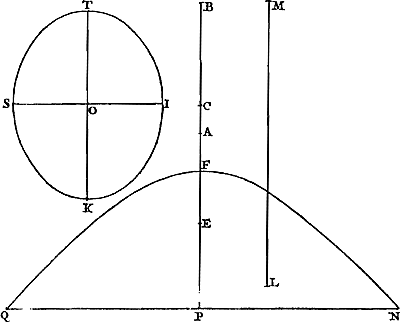 transversum TK habeat ad latus rectum eam rationem, quam linea secundum extremam & mediam rationem secta, ad partem sui majorem.
transversum TK habeat ad latus rectum eam rationem, quam linea secundum extremam & mediam rationem secta, ad partem sui majorem.
Sumatur BC potentia dupla ad SO, item BA potentia dupla ad OK. & sint hae quatuor continue proportionales BC, BA, BF, | BE, &Ga naar margenoot+ ponatur EP aequalis EA. Intelligatur jam conoides hyperbolicum QFN, cujus axis FP; axi adjecta, | |||||||||||||||||||||||||||||||
[pagina 218]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ axe FP, et dont la longueur ajoutée à l'axe, c.à.d. le demi latus transversum, soit FB, tandis que BC représente son latus rectum. La surface courbe de ce conoïde, jointe à celle du sphéroïde SI, sera égale à un cercle de rayon ML, le carré de ML étant égal à la somme du carré TK et de deux fois le carré SIGa naar voetnoot1). | |||||||||||||||||||||||||||||||
Trouver une ligne droite égale à une courbe paraboliqueGa naar voetnoot2).ABC [Fig. 66] représente une portion d'une parabole à axe BK, auquel la base AC est perpendiculaire. On demande de trouver une droite égale à la courbe ABC. Prenons une droite IE [Fig. 67] égale à la demi-base AK et prolongeons-la jusqu'au point H de telle manière que IH soit égale à AG, laquelle, touchant la parabole au point A de la base, coupe l'axe prolongé en G. Soit en autre DEF une portion d'hyperbole décrite avec le sommet E et le centre I, et dont EH représente le diamètre, la base DHF lui étant normale. Le latus rectum est arbitraire. Si l'on suppose maintenant un parallélogramme DPQF construit sur la base DF, lequel soit égal à l'aire DEF, son côté PQ coupera le diamètre de l'hyperbole en R de telle manière que RI sera égale à la courbe parabolique AB, dont ABC est le double. Il apparaît par là comment la mesure de la courbe parabolique dépend de la quadrature de l'hyperbole et réciproquement. Or, un problème quelconque qui se réduit à l'une des deux questions nommées est capable d'une solution numérique aussi approchée qu'on veut par l'admirable invention des logarithmes. En effet, nous avons trouvé jadis que par eux la quadrature de l'hyperbole est résolue numériquement avec une approximation aussi grande qu'on le désireGa naar voetnoot3). Voici notre règle. | |||||||||||||||||||||||||||||||
[pagina 219]
| |||||||||||||||||||||||||||||||
sive ½ latus transversum FB; dimidium latus rectum aequale BC.Ga naar margenoot+ Hujus conoidis superficies curva, unà cum superficie sphaeroidis SI, aequabitur circulo cujus datus erit radius ML, qui nempe possit quadratum TK cum duplo quadrato SIGa naar voetnoot1). | |||||||||||||||||||||||||||||||
Curvae parabolicae aequalem rectam lineam invenireGa naar voetnoot2).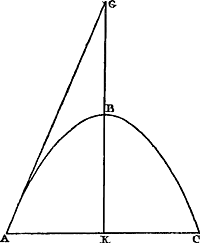 [Fig. 66.]
 [Fig. 67.]
Sit parabolae portio ABC [Fig. 66], cujus axis BK, basis AC axi ad angulos rectos; & oporteat curvae ABC rectam aequalem invenire. Accipiatur basi dimidiae AK aequalis recta IE [Fig. 67], quae producatur ad H, ut sit IH aequalis AG, quae parabolam in puncto basis A contingens, cum axe producto convenit in G. Sit jam portio hyperbolae DEF, vertice E, centro I descriptae, cujusque diameter sit EH; basis vero DHF ordinatim ad diametrum applicata. Latus rectum pro lubitu sumi potest. Quod si jam super basi DF intelligatur parallelogrammum constitutum DPQF, quod portioni DEF aequale sit; ejus latus PQ ita secabit diametrum hyperbolae in R, ut RI sit aequalis curvae parabolicae AB, cujus dupla est ABC. Apparet igitur hinc quomodo à quadratura hyperbolae pendeat curvae parabolicae mensura, & illa ab hac vicissim. Quaecunque vero problemata ad alterum è duobus hisce reducuntur, quamlibetGa naar margenoot+ verae proximam solutionem per numeros accipiunt, logarithmorum admirabili invento. Cum per hos hyperbolae quadratura, ut olim invenimus, numeris quam proxime expliceturGa naar voetnoot3). Est autem regula hujusmodi. | |||||||||||||||||||||||||||||||
[pagina 220]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Soit DAB [Fig. 68] une portion d'hyperbole à asymptotes CS et CV, DE et BV étant des parallèles à l'asymptote SC. Qu'on prenne la différence des logarithmes correspondant à des nombres ayant entre eux les mêmes rapports que les droites DE et BV, et ensuite le logarithme de cette différence. Ajoutons-y le logarithme, qui est toujours le même, 0,36221,56887Ga naar voetnoot1). La somme sera le logarithme du nombre qui représentera l'espace DEVBAD, compris entre trois droites et la courbe DAB, exprimé en parties telles que le parallélogramme DC en a 100000,00000. D'où l'on conclura aussi facilement à l'aire de la portion DAB.
Le nombre correspondant à ce logarithme a 11 chiffres, puisque la caractéristique est 10. Il faut donc d'abord chercher le nombre inférieur, aussi approché que possible, qui correspond au logarithme trouvé: c'est le nombre 19740. Ensuite il faut calculer d'après la différence de ce même logarithme et de celui qui le suit dans la table, les chiffres suivants 81026 que l'on doit écrire à la suite des premiers pour obtenir le nombre total, savoir 197408,10260, où le zéro est ajouté à la fin pour que le nombre des chiffres soit en effet de onze. L'aire de l'espace DEVBAD est donc à fort peu près de 197408,10260 parties, telles que le parallélogramme DC en a 100000,00000. | |||||||||||||||||||||||||||||||
Proposition X.Montrer des lignes courbes telles que par leur évolution soient décrites des ellipses et des hyperboles, et trouver des lignes droites égales à ces courbesGa naar voetnoot3).
Soit AB [Fig. 69] une ellipse ou hyperbole quelconque à axe transversal AC, à centre D, et dont le latus rectum soit le double de AE. Menons à partir d'un point | |||||||||||||||||||||||||||||||
[pagina 221]
| |||||||||||||||||||||||||||||||
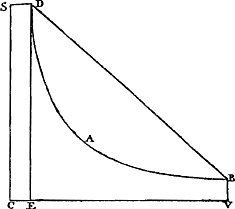 [Fig. 68.]
Sit DAB [Fig. 68] portio hyperbolae,Ga naar margenoot+ cujus asymptoti CS, CV, ductis DE, BV parallelis asymptoto SC. Accipiatur differentia logarithmorum qui conveniunt numeris, eandem inter se rationem habentibus quam rectae DE, BV; ejusque differentiae quaeratur logarithmus. Cui addatur logarith|mus hicGa naar margenoot+ (qui semper est idem) 0,36221,56887Ga naar voetnoot1). Summa erit logarithmus numeri qui spatium DEVBAD designabit, tribus rectis & curva DAB comprehensi, in partibus qualium parallelogrammum DC est 100000,00000. Unde porro facile quoque habebitur area portionis DAB. Sit ex. gr. proportio DE ad BV ea quae 36 ad 5.
Habebit hujus logarithmi numerus 11 characteres, quum characteristica sit 10. Quaeratur itaque primo numerus proxime minor, conveniens invento logarithmo, qui numerus est 19740. Deinde ex differentia logarithmi ejusdem, & proxime eum in tabula sequentis, reliqui characteres eliciantur 81026, scribendi post priores, ut fiat 197408,10260, addito ad finem zero, ut efficiatur numerus characterum 11. Est ergo area spatii DEVBAD proxime partium 197408,10260, qualium partium parallelogrammum DC est 100000,00000. | |||||||||||||||||||||||||||||||
Propositio X.Lineas curvas exhibere quarum evolutione ellipses & hyperbolae describantur, rectasque invenire iisdem curvis aequalesGa naar voetnoot3).
Sit ellipsis vel hyperbole quaelibet AB [Fig. 69] cujus axis transversus AC; centrum figurae D; latus rectum duplum ipsius AE. Et sumpto in sectione quovis puncto, ut | |||||||||||||||||||||||||||||||
[pagina 222]
| |||||||||||||||||||||||||||||||
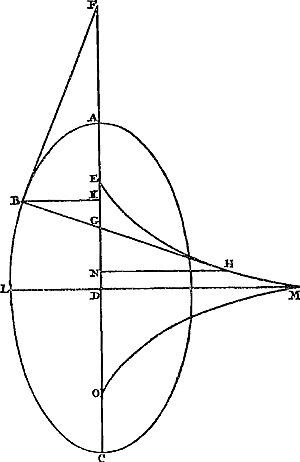
Ga naar margenoot+ [Fig. 69.]
B quelconque de la section l'ordonnée BK et au dit point B une tangente qui coupe l'axe en F. Soit BG perpendiculaire à FB et puisse-t-elle couper l'axe en G. Prolongeons BG jusqu'au point H de telle manière que le rapport BH : HG soit composé des rapports GF : FK et AD : DE. Je dis que la courbe EHM dont tous les points sont trouvés de la même manière que le point H est celle par l'évolution de laquelle, jointe à la droite EA, est décrite la section AB. En d'autres termes que BH touche la courbe en H et est égale à la ligne entière HEA. C'est pourquoi, lorsqu'on retranche EA de HB, la droite qui reste sera égale à l'arc HE. Et il paraît, puisque tous les points de la courbe indifféremment sont trouvés suivant la même méthode bien déterminée, qu'elle est partout du genre de celles qui sont estimées purement géométriques. Il s'ensuit que la relation de tous ses points à ceux de l'axe AC pourra être exprimée par une certaine équation que je trouve monter à la sixième dimension et posséder un minimum de termes lorsque AB est une hyperbole dont le latus transversum et le latus rectum sont égaux; en effet, dans ce dernier cas, si l'on tire d'un point quelconque de la courbe tel que H une perpendiculaire HN à l'axe CAN, et qu'on appelle AC a, CNGa naar voetnoot1) x, et NH y, le cube de x2 - y2 - a2 sera toujours égal à 27x2y2a2. Mais dans ce cas particulier les points de la courbe EHM pourront être trouvés beaucoup plus rapidement, comme cela sera démontré dans la suite. Au reste il faut remarquer que dans le cas de l'ellipse chaque quadrant est décrit par l'évolution d'une ligne correspondante; le quadrant ABL p.e. par l'évolution de la ligne AEHM, le quadrant CL par celle de la ligne COM symétrique avec la précédente. Il y a en effet cette différence entre les deux sections que - tandis que l'origine de la courbe EHM est tant pour l'ellipse que pour l'hyperbole le point E, la droite AE ayant été prise égale à la moitié du latus rectum - dans le cas de l'hyperbole la courbe nommée s'étend à partir du point E jusqu'à l'infini, mais que dans le cas de ellipse elle se termine au point M du petit axe, LM étant prise égale à la moitié du latus rectum, qui se rapporte aux ordonnées perpendiculaires au dit petit axe. Car il | |||||||||||||||||||||||||||||||
[pagina 223]
| |||||||||||||||||||||||||||||||
 [Fig. 69.]
B, applicetur ordinatim ad axem rectaGa naar margenoot+ BK, & ad dictum punctum B tangens ducatur quae conveniat cum axe in F; sitque BG ipsi FB perpendicularis, axique occurrat in G; & producatur BG usque ad H, ut BH ad HG habeat rationem eam quae componitur ex rationibus GF ad FK, & AD ad DE. Dico curvam EHM, cujus puncta omnia inveniuntur eodem modo quo punctum H, esse eam cujus evolutione, unà cum recta EA, describetur sectio AB. Ipsam autem BH tangere curvam in|H, & esse toti HEA aequalem.Ga naar margenoot+ Quamobrem, si ab HB auferatur EA, reliqua recta portioni curvae HE aequabitur. Apparet autem, cum curvae puncta quaevis indifferenter, certaque ratione inveniantur, esse eam utrobique ex earum genere, quae merè geometricae censentur. Unde & relatio horum omnium punctorum ad puncta axis AC, aequatione aliqua exprimi poterit, quam aequationem ad sextam dimensionem ascendere invenio; minimumque habere terminorum, si fuerit AB hyperbola cujus latera transversum rectumque aequalia. Tunc enim ducta ex quovis curvae puncto, ut H, ad axem CAN perpendiculari HN; vocatâque AC, a; CNGa naar voetnoot1), x; & NH, y; erit semper cubus ab xx - yy - aa aequalis 27 xxyyaa. Sed hoc casu brevius quoque multo, quam praedicta constructione, curvae EHM puncta reperiri possunt, ut in sequentibus ostendetur. Caeterum notandum est, in ellipsi singulos quadrantes singularum linearum evolutione describi; sicut quadrans ABL evolutione lineae AEHM, quadrans CL evolutione similis huic oppositae COM. Est enim haec in sectione utraque diversitas, quod cum principium quidem curvae EHM, tam in ellipsi quam in hyperbola, sit punctum E, sumpta AE aequali ½ lateris recti; in hyperbola in infinitum inde dicta linea extenditur, at in ellipsi finitur | in puncto axis minoris M, sumpta LM aequali ½ lateris recti, secundumGa naar margenoot+ quod possunt ordinatim applicatae ad dictum minorem axem. Namque hos ter- | |||||||||||||||||||||||||||||||
[pagina 224]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ apparaîtra facilement à celui qui considère la genèse de cette courbe, que ce sont là ses extrémités, en tenant compte de la proportion AD : DE = LM : MD propre à l'ellipse. Or, nous ne nous arrêterons pas à la démonstration de ces choses, mais nous poursuivrons en enseignant la méthode par laquelle on trouve tant les courbes qui correspondent aux sections coniques que d'autres courbes en nombre infini provenant de courbes données quelconques. | |||||||||||||||||||||||||||||||
Proposition XI.Étant donnée une ligne courbe, en trouver une autre par l'évolution de laquelle elle peut être décrite; et montrer que de toute courbe géométrique provient une autre courbe également géométrique, et qui est rectifiableGa naar voetnoot1).
Soit [Fig. 70] une courbe ou une partie d'elle ABF courbée vers un seul côté, et une droite KL à laquelle tous les points soient rapportés; et qu'il faille trouver une autre courbe telle que DE par l'évolution de laquelle ABF puisse être décrite. Supposons cette courbe déjà trouvée. Puisque toutes les tangentes à la courbe DE doivent être normales à la développante ABF, il est évident que réciproquement toutes les normales à ABF, telles que BD et FE, seront tangentes à la développée CDE. Considérons les points B et F fort proches l'un de l'autre, et puisque l'évolution commence par hypothèse à partir du point A et que F en est plus éloigné que B, le point de contact E sera également plus éloigné du point A que le point D; et l'intersection des droites BD et FE, qui est G, tombera au-delà du point D sur la droite BD. Car il est nécessaire que BD et FE se coupent, puisqu'elles sont normales à la courbe BF du côté où elle est concave. | |||||||||||||||||||||||||||||||
[pagina 225]
| |||||||||||||||||||||||||||||||
minos esse hujus curvae, facile apparebit ortum ejus consideranti, quodque in ellipsiGa naar margenoot+ est sicut AD ad DE, ita LM ad MD. Horum autem demonstrationi non immorabimur, sed ad ipsam methodum tradendam pergemus, qua & hae curvae ex sectionibus conicis, & aliae innumerae ex aliis quibuscunque datis inveniuntur. | |||||||||||||||||||||||||||||||
Propositio XI.Datâ lineâ curvâ, invenire aliam cujus evolutione illa describatur; & ostendere quod ex unaquaque curva geometrica, alia curva itidem geometrica existat, cui recta linea aequalis dari possitGa naar voetnoot1).  [Fig. 70.]
Sit curva quaepiam, vel pars ejus, in partem unam inflexa ABF [Fig. 70], & recta KL, ad quam puncta omnia referantur; & oporteat invenire curvam aliam, ut DE, cujus evolutione ipsa ABF describatur. Ponatur jam inventa; & quoniam tangentes omnes curvae DE, necesse est occurrere lineae ABF, ex evolutione descriptae, ad angulos rectos; patet quoque vicissim eas quae ipsi ABF ad rectos angulos insistunt, ut BD, FE, tacturas evolutam CDE. Intelligantur autem puncta B, F, inter se proxima; & siquidem à parte A evolutioGa naar margenoot+ incipere ponatur, ulteriusque inde distet F quam B, etiam contactus E ulterius quam D distabit ab A; intersectio vero rectarum BD, FE, quae est G, cadet ultra punctum D in recta BD. Nam concurrere ipsas BD, FE necesse est, cum curvae BF ad partem cavam insistant rectis angulis. | |||||||||||||||||||||||||||||||
[pagina 226]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Or, d'autant que le point F sera plus proche du point B, d'autant plus rapprochés seront apparemment aussi les points D, G et E; par conséquent, si l'intervalle BF est considéré comme infiniment petit, les trois points nommés devront être considérés comme n'en formant qu'un seul; en outre, lorsqu'on tire la droite BH qui touche la courbe en B, celle-ci sera estimée être une tangente en F aussi. Soit BO parallèle à KL et BK, FL des perpendiculaires sur cette dernière; puisse FL couper la droite BO en P et soient marqués les points M et N où les droites BD et FE coupent KL. Comme alors le rapport BG : GM est égal au rapport BO : MN, le dernier étant donné, le premier sera également connu: et comme la droite BM est donnée en grandeur et en position, le point G situé sur le prolongement de BM sera également donné; et ce point est identique avec le point D de la courbe CDE puisque, comme nous l'avons dit, G et D coïncidentGa naar voetnoot1). Or, le rapport BO : MN est donné en effet, directement dans le cas de la cycloïde où nous l'avons examiné en premier lieu (et où nous avons trouvé qu'il est de 2:1Ga naar voetnoot2)), par la composition de deux rapports donnés dans les autres courbes que nous avons prises en considération jusqu'aujourd'hui. Car puisque le rapport BO : MN est composé des rapports BO : BP, ou NH : LH, et BP ou KL : MN, il est clair que si ces deux rapports sont donnés, la raison composée des deux BO : MN sera également connue. Mais il apparaîtra bientôt que ces deux rapports sont donnés dans toutes les courbes géométriques, et que par conséquent on peut toujours leur assigner des courbes par l'évolution desquelles elles peuvent être décrites et qui sont par conséquent rectifiables. | |||||||||||||||||||||||||||||||
[pagina 227]
| |||||||||||||||||||||||||||||||
Quanto autem punctum F ipsi B propinquius fuerit, tanto propius quoque punctaGa naar margenoot+ D, G & E convenire apparet; ideoque, si interstitium BF infinite parvum intelligatur, tria dicta puncta pro uno eodemque erunt habenda; ac praeterea, ductâ rectâ BH, quae curvam in B tangat, eadem quoque pro tangente in F censebitur. Sit BO parallela KL, & in hanc perpendiculares cadant BK, FL: secetque FL rectam BO in P, & sint puncta notata M, N, in quibus rectae, BD, FE, occurrant ipsi KL. Quia igitur ratio BG ad GM est eadem quae BO ad MN, data hac dabitur & illa; & quia recta BM datur magnitudine ac positione, dabitur & punctum G in producta BM, sive D in curva CDE, quia G & D in unum convenire diximusGa naar voetnoot1). Datur autem ratio BO ad MN, simpliciter quidem in Cycloide, ubi primùm omnium illam investigavimus, invenimusque duplamGa naar voetnoot2)); in aliis vero curvis, quas hactenus examinavimus, per duarum datarum rationum compositionem. Nam quia ratio BO ad MN componitur ex rationibus BO ad BP, sive NH ad LH, & ex BP sive KL ad MN; patet, si rationes has utraeque dentur etiam ex iis compositam rationem BO ad MN datum iri. Illas vero dari in omnibus curvis geometricis, in sequentibus patebit; ac proinde iis semper curvas adsignari posse, quarum evolutione describantur, quaeque ideo ad rectas lineas sint reducibiles. | |||||||||||||||||||||||||||||||
[pagina 228]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Supposons d'abord [Fig. 71] que ABF soit une parabole de sommet A et d'axe AQ. Puisque les lignes BM et FN sont normales à la parabole et BK et FL à l'axe AQ, d'après une propriété de la parabole, MK et NL seront chacune égale à la moitié du latus rectum; et en retranchant la partie commune LM on aura KL = MN. Par conséquent, attendu que le rapport BG : GM est composé des rapports NH : HL et KL : MN, comme il a été dit, et que le dernier des deux est de 1:1, il est évident que BG : GM = NH : HL; et, par division, BM : MG = NL : LH, ou MK : KH; car LH et KH sont considérées comme identiques à cause de la proximité des points B et F. Or, le rapport MK : KH est donné, lorsque le point B l'est puisque MK et KH sont données chacune en grandeur: MK est égale à la moitié du latus rectum, et KH = 2KA. La droite BM est aussi donnée en position et en grandeur. Par conséquent MG sera aussi donnée et le point G ou D de la courbe RDE également: ce point est trouvé en prolongeant BM jusqu'en G de telle manière qu'on ait: BM : MG = ½ latus rectum: 2KA. De cette manière, un nombre quelconque de points, outre B,ayant été pris sur la parabole ABF, autant de points de la ligne RDE seront trouvés de la même manière; par là même il est évident que la ligne RDE est géométrique et l'on connaît une de ses propriétes d'où les autres peuvent être déduites. Par exemple, si nous voulons demander ensuite, par quelle équation s'exprime la relation de tous les points de la courbe CDE3) à la droite AQ, DQ étant une perpendiculaire sur AQ, le latus rectum de la parabole ABF étant appelé a, AK b, AQ x et QD y, voici ce que nous aurons. Puisque BM : MD, c.à.d. KM : MQ, = ½a : 2b, et que KM = ½a, MQ sera aussi égale à 2b. Or,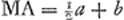 . Par conséquent AQ ou . Par conséquent AQ ou 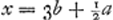 . D'où . D'où 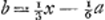 . Ensuite, comme MK2 ou ¼a2 : KB2 ou ab = MQ2 ou 4b2 : QD2, on aura QD2 ou y2 = 16b3/a. Et, en substituant à b l'expression ⅓x - ⅙a qui a été trouvée égale à lui, on obtiendra: . Ensuite, comme MK2 ou ¼a2 : KB2 ou ab = MQ2 ou 4b2 : QD2, on aura QD2 ou y2 = 16b3/a. Et, en substituant à b l'expression ⅓x - ⅙a qui a été trouvée égale à lui, on obtiendra: 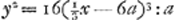 . Par
conséquent . Par
conséquent 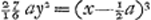 . Prenons sur l'axe de la parabole AR = ½a; on aura alors . Prenons sur l'axe de la parabole AR = ½a; on aura alors 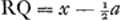 . Il apparaît donc que la courbe CDGa naar voetnoot1) est d'une telle nature que le cube de la ligne RQ est toujours égal à un parallélépipède dont la base est le carré de QD et la hauteur 27/16 a; et . Il apparaît donc que la courbe CDGa naar voetnoot1) est d'une telle nature que le cube de la ligne RQ est toujours égal à un parallélépipède dont la base est le carré de QD et la hauteur 27/16 a; et
| |||||||||||||||||||||||||||||||
[pagina 229]
| |||||||||||||||||||||||||||||||
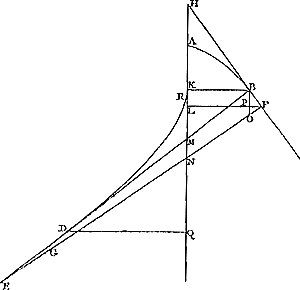 [Fig. 71.]
Ponatur primo parabola esseGa naar margenoot+ ABF [Fig. 71], cujus vertex A, axis AQ. Cum igitur lineae BM, FN, sint parabolae ad angulos rectos; ductaeque sint ad axem AQ perpendiculares BK, FL; erunt, ex proprietate parabolae, singulae MK, NL dimidio lateri recto aequales; & ablata communi LM, aequales inter se KL, MN. Hinc, quum ratio BG ad GM componatur ex rationibus NH ad HL, & KL ad MN, uti dictum suit, sitque earum posterior ratio aequalitatis, liquet rationem BG ad GM fore eandem quae NH ad HL; & dividendo, BM ad MG, eandem quae NL ad LH, sive MK ad KH; nam LH, KH pro eadem habentur, propter propinquitatem punctorum B, F. Data autem est ratio MK ad KH, dato puncto B; quoniam tam MK, quam KH dantur magnitudine; nam MK aequatur dimidio lateri recto, KH vero duplae KA. Dataque etiam est positione & magni|tudine rectaGa naar margenoot+ BM. Ergo & MG data erit, adeoque & punctum G, sive D, in curva RDE; quod nempe invenitur productâ BM usque in G, ut sit BM ad MG sicut ½ lateris recti ad duplam KA. Et sic quidem, adsumptis in parabola ABF aliis quotlibet punctis praeter B, totidem quoque puncta lineae RDE, simili ratione, invenientur; atque hoc ipso lineam RDE geometricam esse constat, unáque proprietas ejus innotescit, ex qua caeterae deduci possunt. Ut si inquirere deinde velimus, quanam aequatione exprimatur relatio punctorumomnium curvae CDEGa naar voetnoot1) ad rectam AQ: ducta in hanc perpendiculari DQ, vocatoque latere recto parabolae ABF, a; AK, b; AQ, x; QD, y. Quoniam ratio BM ad MD, hoc est, KM ad MQ, est ea quae ½a ad 2b, estque ipsa KM ∞ ½a, erit & MQ aequalis 2b. Est autem MA ∞ ½a + b. ergo AQ sive x aequalis 3b + ½a. Unde b ∞ ⅓x - ⅙a. Porro quoniam, sicut quadratum MK, hoc est, ¼aa ad quadratum KB, hoc est, ab, ita qu. MQ, hoc est, 4bb ad qu. QD; erit qu. QD, sive yy ∞ 16b3/a. Ubi, si in locum b substituatur ⅓x - ⅙a, quod illi aequale inventum est, fiet yy ∞ 16. cub. ⅓x - ⅙a divisis per a. Ac proinde 27/16 ayy ∞ cubo ab x - ½a. Accipiatur AR in axe parabolae ∞ ½a; eritque RQ ∞ x - ½a. Curvam igitur CD ejus naturae esse liquet, ut semper cubus lineae RQ aequetur parallelepipedo, cujus basis qu. QD, altitudo 27/16 a; | |||||||||||||||||||||||||||||||
[pagina 230]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ que par conséquent cette courbe est la paraboloïde dont nous avons fait voir plus haut que la parabole AB est la développante, paraboloïde dont le latus rectum est égal à 27/16 fois celui de la parabole AB. En effet, s'il en est ainsi son latus rectum devient égal à 16/27 fois celui de la paraboloïde, comme il a été trouvé en cet endroit. Or, il est manifeste de quelle manière on peut trouver le rapport OB : BP ou NH : HL, non seulement lorsque ABF est une parabole, mais encore lorsque c'est une autre courbe géométrique quelconque. Car il suffira de mener une tangente à la courbe au point considéré F [Fig. 70] et de prendre FN perpendiculaire à FH, par quoi NH et HL seront données et par conséquent aussi leur rapport. Mais il n'est pas aussi évident comment le rapport KL : MN peut être trouvé; toutefois nous montrerons comme suit que cela est toujours possible. Soient les droites KT et LV perpendiculaires à KL, soit KT = KM, LV = LN, et tirons VX parallèle à LN et rencontrant KT en X. Vu que la différence de LK et de NM est toujours la même que celle de LN et de KM, c.à.d. que celle de LV et de KT, et que la différence de LV et de KT est égale à XT, et que XV = LK, il en résulte que NM est égale ou bien à VX + XT ou bien à VX - XT. Par conséquent, si le rapport VX : XT est donné, le rapport VX : VX + XT ou VX : VX - XT, en d'autres termes celui de VX ou LK à MN sera également donné. | |||||||||||||||||||||||||||||||
[pagina 231]
| |||||||||||||||||||||||||||||||
ac proinde ipsam paraboloidem esse, cujus evolutione describi parabolam AB supraGa naar margenoot+ ostendimus; cujus nimirum paraboloidis latus rectum aequetur 27/16 lateris recti parabolae AB. tunc enim hujus latus rectum aequale fit 16/27 lateris recti paraboloidis, quemadmodum ibi fuit definitum. Quomodo porro ratio OB ad BP, sive NH ad HL, non tantum cum ABF parabolaGa naar margenoot+ est, sed etiam alia quaelibet curva geometrica, semper inveniri possit manifestum est. Quoniam tantum recta FH ducenda est, quae curvam in adsumpto puncto F tangat [Fig. 70], & FN ipsi FH perpendicularis: unde NH & HL datae erunt, ac proinde ratio quoque earum data.
[Fig. 70], & FN ipsi FH perpendicularis: unde NH & HL datae erunt, ac proinde ratio quoque earum data.
At non aeque liquet quo pacto ratio KL ad MN innotescat, quam tamen semper quoque reperiri posse sic ostendemus. Sint rectae KT, LV, perpendiculares super KL, sitque KT aequalis KM, & LV aequalis LN, & ducatur VX parallela LN, quae occurrat ipsi KT in X. Quoniam ergo semper eadem est differentia duarum LK, NM, quae duarum LN, KM, hoc est, quae duarum LV, KT; est autem differentiae ipsarum LV, KT aequalis XT, & XV ipsi LK; erit proinde NM aequalis duabus simul VX, XT, vel ei quo VX ipsam XT superat. Atque adeo, si data fuerit ratio VX ad XT, data quoque erit ratio VX ad utramque simul VX, XT, vel ad excessum VX supra XT, hoc est, data erit ratio VX sive LK ad NM. | |||||||||||||||||||||||||||||||
[pagina 232]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Or, il faut savoir que puisque nous avons pris KT = KM et LV = LN, le lieu des points T, V sera une certaine ligne droite ou courbe donnée. Et si c'est une ligne droite, comme c'est le cas lorsque ABF est une section conique, et KL son axe, il est clair que le rapport VX : XT sera donné, étant donnée la position de la ligne VT qui est le lieu des points V, T, et qu'alors le dit rapport a toujours la même valeur quel que soit l'intervalle KL. Mais lorsque le lieu est une autre ligne courbe, le rapport VX : XT sera différent selon que l'intervalle KL sera plus grand ou plus petit. Or, il faut examiner la valeur de ce rapport, lorsque nous nous figurons KL infiniment petite, puis que nous avons aussi supposé les points B et F fort proches l'un de l'autre. Pareillement il faut songer que les points V et T interceptent une partie absolument minime de la ligne courbe; d'où il s'ensuit que la droite VT coïncidera avec celle qui touche la courbe en T. Soit donc TY cette tangente: elle peut être construite puisque la courbe sur laquelle se trouvent les points T et V est géométriqueGa naar voetnoot1). Le rapport YK : KT est donc donné, et par conséquent aussi VX : XT, d'où nous avons montré qu'on peut tirer le rapport LK : NM. On trouve la nature de la ligne passant par les points T et V en prenant un certain point S sur la droite KL et en appelant SK x et KT y. Car puisque la courbe ABF est donnée et que BM est sa normale, on trouvera ainsi par la méthode des tangentes enseignée par DescartesGa naar voetnoot2) la grandeur de la ligne KM que l'on égalera à KT ou y: par cette équation la nature de la courbe TV, à laquelle il faut ensuite mener une tangente, apparaîtra. Mais tout deviendra plus clair par l'exemple suivant. Soit ABF [Fig. 72] la paraboloïde rectifiée plus haut, savoir celle dont les cubes des perpendiculaires sur la droite SK sont entre eux comme les carrés des abscisses situées sur elle, et qu'on demande de trouver la courbe CDE par l'évolution de laquelle la paraboloïde SBF est décrite. Premièrement on trouve aisément le rapport BO : BP parce que nous savons que la tangente en B à la paraboloïde peut être construite en prenant SH = ½SK. Comme BM est normale à cette tangente, les lignes MH et HK sont données, et par conséquent aussi leur rapport qui est égal à OB : BP. | |||||||||||||||||||||||||||||||
[pagina 233]
| |||||||||||||||||||||||||||||||
Sciendum est autem, quoniam KT ipsi KM, & LV ipsi LN, aequales sumptae sunt,Ga naar margenoot+ locum punctorum T, V, fore lineam quandam vel rectam vel curvam datam, ut mox ostendetur. Et siquidem sit linea recta; ut contingit si ABF coni sectio fuerit, & KL axis ejus; constat rationem VX ad XT datam fore, data positione ipsius lineae VT, quae locus est punctorum V, T; semperque ean|dem tunc haberi dictam rationem,Ga naar margenoot+ qualecunque fuerit intervallum KL. At si locus alia linea curva fuerit, diversa erit ratio VX ad XT, prout majus minusve fuerit intervallum KL. Inquirendum est autem quaenam futura sit ista ratio, cum KL infinite parvum imaginamur, quoniam & puncta B, F, proxima invicem posuimus. Similiter itaque & puncta V, T, lineae curvae minimam particulam intercipere intelligendum est; unde recta VT, cum ea quae in T curvam contingit, coincidet. Sit ergo tangens illa TY; potest enim duci quoniam curva, ad quam sunt puncta T, V, geometrica estGa naar voetnoot1). Ratio igitur YK ad KT data erit, adeoque & VX ad XT. ex qua etiam rationem LK ad NM dari ostendimus. Quaenam vero sit linea ad quam sunt puncta T, V, invenitur ponendo certum punctum S in recta KL, & vocando SK, x; KT, y. Nam quia data est curva ABF, eique BM ad angulos rectos ducta, invenietur inde quantitas lineae KM, per methodum tangentium à Cartesio traditamGa naar voetnoot2), quae ipsi KT, sive y aequabitur, & ex ea aequatione, natura curvae TV innotescet, ad quam deinde tangens ducenda est. Sed clariora omnia sient sequenti exemplo.
BM ad angulos rectos ducta, invenietur inde quantitas lineae KM, per methodum tangentium à Cartesio traditamGa naar voetnoot2), quae ipsi KT, sive y aequabitur, & ex ea aequatione, natura curvae TV innotescet, ad quam deinde tangens ducenda est. Sed clariora omnia sient sequenti exemplo.
Sit ABF [Fig. 72] paraboloides illa, cuisuperius rectam aequalem invenimus; in qua nempe cubi perpendicularium in rectam SK, sint inter se sicut quadrata ex ipsa SK abscissarum. Et oporteat invenire curvam CDE cujus evolutione paraboloides SBF describatur. Hic primum ratio BO ad BP facile invenitur, quia tangentem paraboloidis in puncto B duci scimus, sumpta SH aequali ½ SK. Cui tangenti cum BM ad angulos rectos insistat, dantur jam lineae MH, HK, ac proinde earum inter se ratio, quae est eadem quae OB ad BP. | |||||||||||||||||||||||||||||||
[pagina 234]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ Pour calculer ensuite le rapport de BP ou KL à MN tirons normalement à KL les droites KT et LV égales respectivement à KM et LN dont la dernière sera la plus grande des deux; et soit VX parallèle à LK. Puisqu'alors 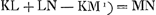 Ga naar voetnoot1) - où l'on peut aussi de XV + VL ou XV + XK retrancher KT, ce qui donne le reste VX + XT - on aura Ga naar voetnoot1) - où l'on peut aussi de XV + VL ou XV + XK retrancher KT, ce qui donne le reste VX + XT - on aura 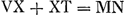 ; partant le rapport KL: MN sera égal à VX : VX + XT. Et pour trouver la valeur de ce rapport lorsque l'intervalle KL est extrêmement petit, il faut suivant ce qui a été dit plus haut chercher quel est le lieu ou la ligne des points T, V. Appelons à cet effet a le latus rectum de la paraboloïde et soit SK = x, KT = y. ; partant le rapport KL: MN sera égal à VX : VX + XT. Et pour trouver la valeur de ce rapport lorsque l'intervalle KL est extrêmement petit, il faut suivant ce qui a été dit plus haut chercher quel est le lieu ou la ligne des points T, V. Appelons à cet effet a le latus rectum de la paraboloïde et soit SK = x, KT = y.
Comme KH, KB et KM sont alors proportionnelles et que HK = 3/2 x, tandis que d'après la nature de la paraboloïde KB = ∛ax2, KM ou KT deviendra égale à ⅔ ∛a2x. Donc ⅔ ∛a2x = y, partant 8/27 a2x = y3. D'où il apparaît que le lieu des points T, V est cette paraboloïde que les géomètres appellent cubique. On y mènera une tangente au point T en prenant SY = 2SK, et en joignant Y et T par une droite. Le rapport VX : VX + XT, que nous avons dit être égal à KL : MN, sera maintenant celui de YK à YK + KT. Or, ce dernier rapport est donné, par conséquent aussi le rapport KL : MN. Mais il a été démontré que le rapport OB : PB est également connu. Comme le rapport BD : DM est composé des deux rapports en question, ainsi que cela est apparu plus haut, le rapport BD : DM sera lui aussi connu; et, par division, on connaîtra le rapport BM : MD et par conséquent aussi le point D de la courbe DE. Or, c'est ainsi qu'on parviendra à la construction la plus courte. KT ou KM a été appelée y. On aura donc . Et MH : HK, ou OB : BP, = y + 3/2 x : 3/2 x, ou en doublant les termes = 2y + 3x : 3x. Ensuite, parce que YK = 3x, on aura YK : YK + KT, ou YK : KL + MN d'après ce qui a été dit plus haut, = 3x : 3x + y. Mais nous avons dit que le rapport BD : DM est composé des rapports OB : BP et KL : MN. Le rapport BD : DM sera donc composé des rapports 2y + 3x : 3x et 3x : 3x + y, et sera par conséquent égal à 2y + 3x : 3x + y; et, par division, on aura . Et MH : HK, ou OB : BP, = y + 3/2 x : 3/2 x, ou en doublant les termes = 2y + 3x : 3x. Ensuite, parce que YK = 3x, on aura YK : YK + KT, ou YK : KL + MN d'après ce qui a été dit plus haut, = 3x : 3x + y. Mais nous avons dit que le rapport BD : DM est composé des rapports OB : BP et KL : MN. Le rapport BD : DM sera donc composé des rapports 2y + 3x : 3x et 3x : 3x + y, et sera par conséquent égal à 2y + 3x : 3x + y; et, par division, on aura  .
Soit SZ perpendiculaire à SK et que MB prolongée la coupe en Z. Comme le rapport BM : MD a été trouvé égal à y : y + 3x, c.à.d. à MK : MK + 3 KS, et qu'à ce dernier rapport est égal le rapport MB: MB + 3BZ. on aura par conséquent .
Soit SZ perpendiculaire à SK et que MB prolongée la coupe en Z. Comme le rapport BM : MD a été trouvé égal à y : y + 3x, c.à.d. à MK : MK + 3 KS, et qu'à ce dernier rapport est égal le rapport MB: MB + 3BZ. on aura par conséquent 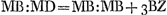 . D'où il appert que MD doit être prise égale à MB + 3BZ. Et de la même manière on pourra trouver un nombre quelconque de points de la courbe CDE. Un arc quelconque de cette courbe tel que DS sera égal à la droite DB qui est normale à la paraboloïde SAB. Il est certain que la courbe trouvée est géométrique et, si nous le voulons, nous pouvons exprimer par une équation la relation de tous ses points à ceux de l'axe SK. . D'où il appert que MD doit être prise égale à MB + 3BZ. Et de la même manière on pourra trouver un nombre quelconque de points de la courbe CDE. Un arc quelconque de cette courbe tel que DS sera égal à la droite DB qui est normale à la paraboloïde SAB. Il est certain que la courbe trouvée est géométrique et, si nous le voulons, nous pouvons exprimer par une équation la relation de tous ses points à ceux de l'axe SK.
De la même manière, si nous faisons cette recherche pour la paraboloïde ou parabole cubique [Fig. 73] dont les cubes des ordonnées perpendiculaires à l'arc sont | |||||||||||||||||||||||||||||||
[pagina 235]
| |||||||||||||||||||||||||||||||
Ut autem ratio BP, sive KL ad MN innotescat, ponantur ad KL perpendiculairesGa naar margenoot+ rectae KT, LV, aequales singulis KM, LN, sitque VX parallela LK. Jam quia ex duabus simul KL, LN, auferendo KM, relinquitur MNGa naar voetnoot1); hoc est, auferendo ex duabus XV, VL, sive XV, XK, ipsam KT; hinc autem relinqui apparet VX & XT: erunt igitur hae duae VX, XT ipsi MN aequales, ac proinde ratio KL ad MN eadem quae VX ad duas simul VX, XT. Ut autem haec ratio innotescat cum intervallum KL est minimum; oportet secundum praedicta inquirere quis sit locus, sive linea ad quam sunt puncta T, V. Quod ut fiat sit latus rectum paraboloidis ABF ∞ a; SK ∞ x; KT ∞ y. Quia igitur proportionales sunt KH, KB, KM, estque HK ∞ | ½x: KB ex naturaGa naar margenoot+ paraboloidis aequalis R. cub. axx: fiet KM, hoc est KT ∞ ⅔ R. cub. aax ∞ y, ac proinde 8/27 aax ∞ y3. Unde patet locum punctorum T, V, esse paraboloidem illam, quam cubicam vocant geometrae. Cui proinde ad T tangens ducetur, sumptâ SY duplâ ipsius SK, junctâque YT. Et jam quidem ratio VX ad duas simul VX, XT, quam diximus eandem esse ac KL ad MN, erit ea quae YK ad utramque simul YK, KT. Haec autem ratio data est, ergo & ratio KL ad MN. Sed & rationem OB ad PB datam esse ostensum est. Ergo, cum ex duabus hisce componatur ratio BD ad DM, ut supra patuit, dabitur & haec; & dividendo, ratio BM ad MD; adeoque & punctum D in curva DE. Ad constructionem autem brevissimam hoc pacto hic perveniemus. KT sive KM dicta fuit y. Itaque MH erit y + 3/2 x. Et MH ad HK, sive OB ad BP, ut y + 3/2 x ad 3/2 x. sive, sumptis omnium duplis, ut 2y + 3x ad 3x. Deinde quia YK ∞ 3x, erit YK ad YK + KT, sive per praedicta, KL ad MN, ut 3x ad 3x + y. Atqui ex rationibus OB ad BP, & KL ad MN, componi diximus rationem BD ad DM. Ergo ratio BD ad DM erit composita ex rationibus 2y + 3x ad 3x, & 3x ad 3x + y; ideoque erit ea quae 2y + 3x ad 3x + y. & dividendo, ratio BM ad MD, eadem quae y ad 3x + y. Sit SZ perpendicularis ad SK, eique occurrat MB producta in Z. | Quia ergo ratioGa naar margenoot+ BM ad MD inventa est ea quae y ad y + 3x, hoc est quae MK ad MK + 3KS. Sicut autem MK ad MK + 3 KS, ita MB ad MB + 3 BZ; erit proinde MB ad MD ut MB ad MB + 3 BZ. Unde liquet MD aequalem sumendam ipsi MB + 3 BZ. Atque ita quotlibet puncta curvae CDE invenire licebit. Cujus curvae portio quaelibet ut DS, rectae DB, quae paraboloidi SAB ad angulos rectos occurrit, aequalis erit. Constat autem geometricam esse, & si velimus, possumus aequatione aliqua relationem exprimere punctorum omnium ipsius ad puncta axis SK. Simili modo autem, si inquiramus in paraboloide illa sive parabola cubica [Fig. 73], in qua cubi ordinatim applicatarum ad axem, sunt inter se sicut portiones axis abscissae, | |||||||||||||||||||||||||||||||
[pagina 236]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ entre eux comme les abscisses qui sont situées sur lui, nous trouverons que la courbe par l'évolution de laquelle elle est décrite et qui est par conséquent rectifiable, est déterminée par points par une construction nullement plus difficile. En effet, soit SAB cette parabole cubique, SM son axe (or, c'est improprement qu'on parle d'un axe dans le cas de cette courbe, puisque sa forme est telle que, lorsqu'on tire SZ perpendiculairement à SM, SZ a des parties semblables de la courbe situées de part et d'autre). Tirons par un point B quelconque pris sur la paraboloïde la droite BD qui lui soit normale et coupe l'axe en M, la droite SZ en Z. Prenons ensuite 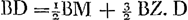 BZ. D sera alors un des points de la courbe cherchée RD ou RI par l'évolution de laquelle, après qu'on y a encore ajouté une certaine droite RA, la paraboloïde SAB sera décrite. Or, il y a ici, ce qui mérite d'être remarqué, et ce qui arrive aussi dans le cas de certaines autres paraboloïdes de ce genre, deux évolutions de sens opposés, dont l'une et l'autre se fait à partir du point déterminé A; de sorte que par l'évolution de ARD prolongée jusqu'à l'infini la branche infinie ABF de la paraboloïde est décrite, mais par l'évolution de ARI qui s'étend également jusqu'à l'infini, seulement l'arc AS. Quant au point A, on le détermine en prenant SP de telle grandeur que son rapport au latus rectum de la paraboloïde soit égal à celui de l'unité à BZ. D sera alors un des points de la courbe cherchée RD ou RI par l'évolution de laquelle, après qu'on y a encore ajouté une certaine droite RA, la paraboloïde SAB sera décrite. Or, il y a ici, ce qui mérite d'être remarqué, et ce qui arrive aussi dans le cas de certaines autres paraboloïdes de ce genre, deux évolutions de sens opposés, dont l'une et l'autre se fait à partir du point déterminé A; de sorte que par l'évolution de ARD prolongée jusqu'à l'infini la branche infinie ABF de la paraboloïde est décrite, mais par l'évolution de ARI qui s'étend également jusqu'à l'infini, seulement l'arc AS. Quant au point A, on le détermine en prenant SP de telle grandeur que son rapport au latus rectum de la paraboloïde soit égal à celui de l'unité à  (lequel nombre est le cube de 45) et en tirant l'ordonnée correspondante
PA. En partant de là, on trouvera ensuite
le point R, extrémité commune des deux courbes RD et RI, comme tous les autres points de ces courbes, c.à.d. comme le point D a été trouvé tout-à-l'heure. (lequel nombre est le cube de 45) et en tirant l'ordonnée correspondante
PA. En partant de là, on trouvera ensuite
le point R, extrémité commune des deux courbes RD et RI, comme tous les autres points de ces courbes, c.à.d. comme le point D a été trouvé tout-à-l'heure.
Enfin, quelle que soit dans la famille des paraboloïdes la courbe SAB, nous avons trouvé qu'on peut toujours avec la même facilité trouver par points une autre courbe par l'évolution de laquelle elle peut être décrite et qui est par conséquent rectifiable. Nous représentons donc dans la table qui suit, et qui peut s'étendre jusqu' où l'on voudra, la construction universelle.
Soit SB [Fig. 74] une parabole ou paraboloïde à sommet S, et SK l'axe (ou bien une perpendiculaire à l'axe) auquel soient rapportés parune équation les points de la paraboloïde. Nous supposons toujours SK tiré du côté concave, et SZ perpendiculaire à lui. Etant posée maintenant SK = x, BK = y, laquelle est la perpendiculaire à SK à partir d'un point quelconque, et le latus rectum de la courbe = a, la première colonne de la table, celle de gauche, explique la nature de chaque paraboloïde par son | |||||||||||||||||||||||||||||||
[pagina 237]
| |||||||||||||||||||||||||||||||
inveniemus curvam cujus evolutione describitur, quaeque proinde rectae lineae aequariGa naar margenoot+ poterit, nihilo difficiliori constructione per puncta determinari. Nam si fuerit illa SAB; axis SM; (dicitur autem improprie axis in hac curva, cum forma ejus sit ejusmodi, ut ductâ SZ, quae secet SM ad angulos rectos, ea portiones similes curvae habeat ad partes oppositas;) agatur per punctum quodlibet B, in paraboloide sumptum, recta BD, quae
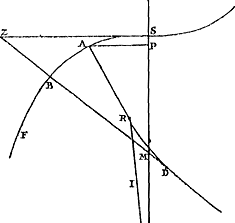 curvam ad angulos rectos secet, axique ejus occurrat in M, rectae vero SZ in Z. Deinde sumatur BD aequalis dimidiae BM, unà cum sesquialtera BZ. Eritque D unum è punctis curvae quaesitae RD vel RI, cujus evolutione, juncta tamen recta quadam RA, describetur paraboloides SAB. Sunt autem hic, quod notatu dignum est, quodque in aliis etiam nonnullis harum paraboloidum contingit, duae evolutiones in partes contrarias, quarum utraque à puncto certo A initium capit; ita ut evolutione ipsius ARD, in infinitum porro continuatae, describatur paraboloidis pars infinita ABF; evolutione autem totius ARI, similiter in infinitum extensae, tantum particula AS. Punctum autem A definitur, sumptâ SP quae sit ad | latus rectum paraboloidis, sicut unitas ad radicem quadrato-quadraticamGa naar margenoot+ numeri 91125, (is cubus est ex 45) applicatâque ordinatim PA. Unde porro punctum R, confinium duarum curvarum RD, RI, invenitur sicut caetera omnia harum curvarum, hoc est, sicut punctum D modo inventum fuit.
curvam ad angulos rectos secet, axique ejus occurrat in M, rectae vero SZ in Z. Deinde sumatur BD aequalis dimidiae BM, unà cum sesquialtera BZ. Eritque D unum è punctis curvae quaesitae RD vel RI, cujus evolutione, juncta tamen recta quadam RA, describetur paraboloides SAB. Sunt autem hic, quod notatu dignum est, quodque in aliis etiam nonnullis harum paraboloidum contingit, duae evolutiones in partes contrarias, quarum utraque à puncto certo A initium capit; ita ut evolutione ipsius ARD, in infinitum porro continuatae, describatur paraboloidis pars infinita ABF; evolutione autem totius ARI, similiter in infinitum extensae, tantum particula AS. Punctum autem A definitur, sumptâ SP quae sit ad | latus rectum paraboloidis, sicut unitas ad radicem quadrato-quadraticamGa naar margenoot+ numeri 91125, (is cubus est ex 45) applicatâque ordinatim PA. Unde porro punctum R, confinium duarum curvarum RD, RI, invenitur sicut caetera omnia harum curvarum, hoc est, sicut punctum D modo inventum fuit.
Denique, quaecunque fuerit ex paraboloidum genere curva SAB, semper aeque facile curvam aliam, cujus evolutione ipsa describatur, quaeque propterea rectae adaequari possit, per puncta inveniri comperimus. Atque adeo constructionem universalem sequenti tabella exhibemus, quae quousque libuerit extendi poterit.
Sit SB [Fig. 74] parabola, vel paraboloidum aliqua, cujus vertex S; recta SK vel axis, vel axi perpendicularis, ad quam referuntur aequatione puncta paraboloidis; & ipsa quidem SK semper ad partem cavam ducta intelligitur; cui perpendicularis SZ. Ponendo jam SK ∞ x; BK ∞ y, quae à puncto quovis curvae perpendicularis est ipsi SK; & latere recto curvae ∞ a; prior pars tabellae, quae ad sinistram est, naturam | |||||||||||||||||||||||||||||||
[pagina 238]
| |||||||||||||||||||||||||||||||
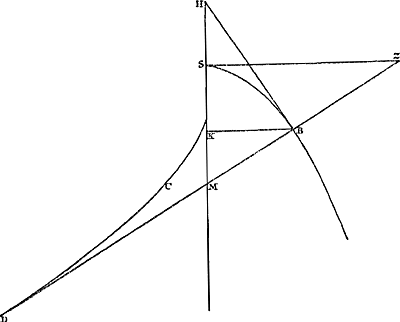
Ga naar margenoot+ [Fig. 74.]
équation. À ces équations correspondent dans la colonne droite les longueurs de la ligne BD laquelle placée normalement sur la courbe SB fournira le point D de la courbe cherchée CD. Par exemple, si SB est la parabole qui provient de la section du cône, nous savons que son équation est la première de la table, savoir ax = y2, à laquelle correspond dans l'autre colonne 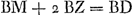 . D'où est connue la longueur de la ligne BD, et par conséquent aussi la méthode de trouver un nombre quelconque de points de la courbe CD. Il a été démontré plus haut que dans ce cas-ci cette développée est une paraboloïde, savoir celle dont l'équation est la troisième de cette table. . D'où est connue la longueur de la ligne BD, et par conséquent aussi la méthode de trouver un nombre quelconque de points de la courbe CD. Il a été démontré plus haut que dans ce cas-ci cette développée est une paraboloïde, savoir celle dont l'équation est la troisième de cette table.
Or, la table est construite de cette manière qu'on donne à BM pour coëfficient l'exposant de x dans l'équation, et à BZ celui de y, et qu'on divise ensuite la somme des deux termes par l'exposant de aGa naar voetnoot1).
Outre ces lignes paraboloïdiques nous en avons trouvé d'autres d'où l'on déduit des courbes rectifiables par une construction à peu près semblable. Elles ressemblent à des hyperboles en ceci qu'elles ont des asymptotes qui toutesois font toujours entre elles un angle droit. Nous considérons comme la première d'entre elles l'hyperbole ordinaire qui provient de la section du cône. Pour expliquer la nature des autres, soient PS et KS [Fig. 75] les asymptotes de la courbe AB, comprenant entre elles un angle droit, et tirons à partir d'un point | |||||||||||||||||||||||||||||||
[pagina 239]
| |||||||||||||||||||||||||||||||
singularum paraboloidum singulis aequationibus explicat. Quibus respondent in parteGa naar margenoot+ dextra quantitates lineae BD, quae si curvae SB insistat ad angulos rectos, exhibitura sit punctum D | in curva quaesita CD. Exempli gratia, si SB est parabola quae ex coniGa naar margenoot+ sectione fit, ei scimus convenire aequationem tabellae primam, ax ∞ y2; cui respondet ab altera parte BM + 2BZ ∞ BD. Unde longitudo lineae BD cognoscitur, adeoque inventio quotlibet punctorum curvae CD. Quam quidem, hoc casu, paraboloidem esse supra demonstratum fuit, eam nempe, cujus aequatio tertia est hujus tabellae. Construitur autem tabella hoc pacto, ut BM sumatur multiplex secundum numerum qui est exponens potestatis x in aequatione; BZ vero, multiplex secundum exponentem potestatis y; ex his autem utrisque compositae accipiatur pars denominata ab exponente potestatis aGa naar voetnoot1).
Praeter hasce autem paraboloides lineas, alias item invenimus, à quibus, non absimili constructione, deducuntur curvae rectis comparabiles. Assimilantur autem hyperbolis, eo quod asymptotos suas habent, sed tantum angulum rectum constituentes. Et harum primam quidem statuimus hyperbolam ipsam, quae est è coni sectione. Reliquarum vero naturam ut explicemus; sunto PS, SK [Fig. 75], asymptoti curvae AB, rectum angulum comprehendentes, & à curvae puncto quolibet B ducatur
| |||||||||||||||||||||||||||||||
[pagina 240]
| |||||||||||||||||||||||||||||||
Ga naar margenoot+ quelconque B de la courbe la droite BK parallèle à PS. Soit SK = x et KB = y. Dans le cas où AB est une hyperbole nous savons que le rectangle des lignes SK et KB, c.à.d. le rectangle xy, est toujours égal au même carré que nous pouvons appeler a2. L'hyperboloïde qui la suit sera celle pour laquelle le solide exprimé par la multiplication de la ligne SK par la hauteur KB, c.à.d. le solide x2y, est égal à un certain cube que nous pouvons désigner par a3. Il existe encore d'autres hyperboloïdes en nombre infini du même genre; la table suivante exprime la propriété de chacune d'elles par son équation, et en même temps la méthode de construction de la courbe DC par l'évolution de laquelle elle est produite.
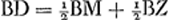 , comme la table l'indique; le point D se trouvera alors sur la courbe cherchée DC, dont on pourra trouver d'autres points en nombre quelconque de la même manière et dont chaque partie peut être égalée à une ligne droite. Et cette courbe DC est la même que celle dont nous avons exprimé plus haut par une équation la relation à l'axe de l'hyperbole. Or, la construction de cette table est entièrement la même que celle de la table précédenteGa naar voetnoot1). , comme la table l'indique; le point D se trouvera alors sur la courbe cherchée DC, dont on pourra trouver d'autres points en nombre quelconque de la même manière et dont chaque partie peut être égalée à une ligne droite. Et cette courbe DC est la même que celle dont nous avons exprimé plus haut par une équation la relation à l'axe de l'hyperbole. Or, la construction de cette table est entièrement la même que celle de la table précédenteGa naar voetnoot1).
Au reste, puisqu'il faut, tant pour la construction de ces courbes que pour celles qui proviennent des paraboloïdes, tirer les lignes DBZ coupant au point donné B les courbes AB ou leurs tangentes à angles droits, nous dirons en général comment on trouve ces tangentes. À cet effet il faut considérer dans l'équation qui exprime la nature de chaque courbe - ces équations sont données dans les deux tables précédentes - quels sont les exposants de x et de y et prendre SK : KH = exposant de x: exposant de y. Une droite qui joint les points H et B touchera alors la courbe au point B. Dans le cas de la troisième hyperboloïde par exemple, dont l'équation est xy2 = a3, comme l'exposant de x est 1 et celui de y 2, il faut que SK : KH = 1:2Ga naar voetnoot2). Ceux qui se sont appliqués à l'art analytique connaissent la démonstration de cette proposition: ils ont commencé depuis longtemps à considérer ces lignes et ont mesuré les lieux plans et solides non seulement de ces paraboloïdes, mais aussi de quelques espaces s'étendant jusqu'à l'infini compris entre les hyperboloïdes et leurs asymptotes. C'est ce que nous pourrions exécuter nous aussi d'après une méthode facile et universelle, la démonstration étant dérivée de la seule propriété des tangentesGa naar voetnoot3). Mais ces choses ne sont pas de ce lieu. | |||||||||||||||||||||||||||||||
[pagina 241]
| |||||||||||||||||||||||||||||||
BK parallela PS, sitque SK ∞ x; KB ∞ y. Si igitur hyperbola sit AB, scimus rectangulumGa naar margenoot+ linearum SK, KB, hoc est, rectangulum xy semper eidem quadrato aequale esse, quod vocetur aa. Proxima vero hyperboloidum erit, in qua solidum ex quadrato | lineae SK, in altitudinemGa naar margenoot+ KB ductum, hoc est, solidum xxy, cubo certo aequabitur, qui vocetur a3. Atque ita innumerae aliae hujus generis hyperboloides existunt, quarum proprietatem sequens tabella singulis aequationibus exhibet, simulque rationem construendi curvam DC, cujus evolutione quaeque generetur.
Recta DBMZ curvam AB, ut antea quoque, secat ad angulos rectos, occurritque asymptotis SK, SP, in M & Z. Si igitur exempli gratia hyperbola fuerit AB, cujus aequatio est xy ∞ a2, sumetur BD ∞ ½BM + ½BZ, quemadmodum tabella praecipit. Eritque punctum D in curva DC quaesita, cujus alia quotlibet puncta sic inveniri poterunt, & portio ejus quaelibet rectae lineae adaequari. Et haec quidem eadem illa est curva, cujus relationem ad axem hyperbolae superius aequatione expressimus. Constructio autem tabellae hujus plane eadem est quae superiorisGa naar voetnoot1). Caeterum, quoniam tum ad harum curvarum, tum ad earum quae ex paraboloidibus nascuntur constructionem, ducendae sunt lineae DBZ, quae ad datum punctum B secent curvas AB, sive ipsarum tangentes BH, ad angulos rectos; dicemus in universum quomodo hae tangentes inveniantur. In aequatione itaque, quae cujusque curvae naturam explicat, quales aequationes duabus tabellis praecedentibus exponuntur, considerare oportet quae sint exponentes potestatum x & y, & facere ut, sicut exponens potestatis x ad exponentem potestatis y, ita sit SK ad KHGa naar voetnoot2). Juncta enim HB curvam in B continget. Velut in tertia hyperboloide, cujus aequatio est xy2 ∞ a3: quia exponens potestatis x est 1, potestatis autem y exponens 2; oportet esse ut 1 ad 2 ita SK ad KH. Horum autem demonstrationem noverunt analyticae artis periti, qui jam pridem omnes has lineas contemplari coeperunt; & non solum paraboloidum istarum, sed & spatiorum quorundam infinitorum, inter hyperboloides & asymptotos interjectorum, plana solidaque dimensi sunt. Quod quidem & nos, facili atque universali methodo, expedire possemus, ex sola tangentium proprietate sumpta demonstrationeGa naar voetnoot3). Sed illa non sunt hujus loci. |
| ||||||||||||||||||||||||||||||