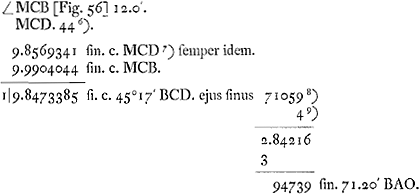|
| |
| |
| |
Appendice X
Au traité des couronnes et des parhéliesGa naar voetnoot1).
ἀγεωμέτρητοι haec neque invenire possunt neque inventa intelligereGa naar voetnoot2).
| |
[Fig. 54.]
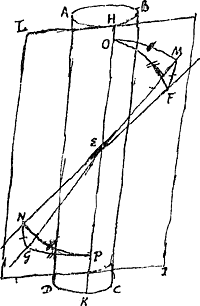
Ad demonstrationem brevissimam circuli albi, qui horizonti parallelus in pareliorum phaenomenis. In Cylindrum ABCD [Fig.54] perpendiculariter erectum incidat radius a solis centro adveniens FE, qui reflectatur secundum rectam EG. dico FE, EG aequalibus angulis inclinari ad planum horizontis. Sit enim latus cylindri per punctum reflexionis E ductum HK, secundum quod tangi cylindrus intelligatur plano LI. Constat itaque radium FE eodem modo a plano hoc reflecti atque a cylindro ABCD, hoc enim in dioptricis axiomatis loco est qualiscunque fuerit curvaGa naar voetnoot4) superficies reflectens. Quod si jam plano LI aliud planum ad rectos angulos insistere ponatur, quod in se contineat radios FE, EG, constat etiam ex legibus dioptricis utriusque plani communem intersectionem, quae sit recta MN, transire per punctum reflexionis E, angulosque aequales esse FEM, GEN. Intelligatur itaque sphaerica superficies cujus E centrum, quae abscindat rectas aequales EF, EM, EO, itemque EG, EN, EP, quarum nempe EO, EP sint in recta HK. Sintque circulorum maximorum in sphaerae superficie arcus FO, FM, OM; itemque GP, GN, PN. Quia igitur planum per FMNG ductum rectum est ad planum LI, et utrumque per sphaerae centrum E transit; sunt autem in plano per FMNG arcus FM, GN; et in plano LI arcus MO, NP; erunt in triangulo sphaerico FMO rectus angulus M, et in triangulo GNP rectus angulus N. latus autem MO aequale est lateri NP, quia angulus MEO aequalis NEP.
| |
| |
Itemque latus MF aequale lateri GN, quia aequales anguli FEM, GEN. Itaque et latus reliquum FO aequale erit lateri reliquo GP. ac proinde angulus FEO aequalis angulo GEP. Quorum complementa ad angulum rectum cum sint anguli inclinationis ad horizontem radiorum FE, EG etiam isti inclinationis ad horizontem anguli aequales erunt. quod erat demonstrandum.
Eadem est demonstratio cum radius FE est intra cylindrum, et a superficie ejus reflectitur quod ad parelia pertinet ut ostendatur ea in circulo albo cerni debereGa naar voetnoot5).
| |

[Fig. 55.]
Dans la Fig. 55 EF est un des rayons du soleil tombant sur le cylindre vertical d'eau ou de glace contenant un noyau cylindrique de rayon NU. Le rayon EF se réfracte en FG qui frise le noyau; après une deuxième réfraction ce rayon quitte le cylindre suivant GH. La projection des trois parties du rayon sur la base horizontale du cylindre est KCGL. C'est l'angle aigu β formé par les droites CK et LG qu'il s'agit de calculer. Le plan DIPC touche le cylindre suivant la génératrice DC, passant par le point F. Le plan IEFQG, perpendiculaire au plan tangent nommé, et dans lequel EI, SF et QG font un angle droit avec DC, contient le rayon incident EF et le rayon réfracté FG. Dans la figure on a pris FE = FG (= a), de sorte que DF = n. FC, où n représente l'indice de réfraction. ∠ FED ou α est la hauteur du soleil au-dessus de l'horizon. Donc DF = a sin α. Soit NU/NG (rapport du rayon du
| |
| |
noyau à celui du cylindre entier) = m. On a 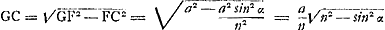 . Les triangles NUG et CQG étant semblables, on a  . On tire ensuite des triangles semblables FCQ et FDI :  . Or DE = a cos α. Donc sin 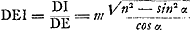 . L'angle DEI est égal à l'angle TCN. L'angle β qu'il s'agit de trouver est le double de la différence de l'angle TCN et de l'angle GCN (c.à.d. le double de l'angle GCT), donc

Ad inveniendum angulum verticalium circulorum per solem et per parelium alterutrum quod soli est à latereGa naar voetnoot7).
sit solis altitudo 10o.
| |
| |
D'après la table du § 17 (voir la p. 401 qui précède) la plus grande distance β d'un parhélie latéral au soleil, pour m = 0,680, est de 94o22′; la hauteur α du soleil serait alors de 35o.
En effet, la formule β = 2 [ arc sin m N - arc sin m], où  , nous apprend que pour m = 0,68, N a tout au plus la valeur 1/0,68. On en tire (pour n = 250/187) α = 34 o40′ à peu près, et ensuite β = 94 o20′.
D'après la même table, lorsqu'on prend α = 25 o, l'angle β est tout au plus de 88 o48′, et la proportion m aurait alors la valeur 0.714. En effet, dans ce cas N = 1,4 à fort peu près, et m a donc tout au plus la valeur 1/1,4 ou 0,714. On trouve ensuite  .
| |
| |
| |
§ 3.
∠ MCB [Fig. 56] supponiturGa naar voetnoot22), inde inveniuntur ∠ BAE altitudo ☉. et ∠ CLP, qui est arcus horizontis interceptus inter verticalem per ☉ et verticalem per parelium. assumitur autem cylindri glaciati certa crassitudo, ad cylindrum aqueum ut hic subdupla.
| |
| |

[Fig. 56.]
Paradigma. ∠ MCB 12 gr.
| |
| |
| |
| |
| |
CDF horizon. A spectator. Z zenith [Fig. 57]Ga naar voetnoot37). ∠ BAC altitudo parelij aequalis altitudini solis. ZD circulus verticalis inter duo parelia medius transiens.

[Fig. 57.]
| |
| |
ZBC, ZEF circuli verticales per parelia transeuntes.
Haec sunt parelia quae in parte coeli quae soli opposita est spectantur.
Cum angulus BAC hoc est altitudo solis veri supra horizontem est 22. gr. invenio angulum DAC vel DAFGa naar voetnoot36) gr. 37½. unde distantia pareliorum erit 68o 44′Ga naar voetnoot38).
Cum angulus BAC est 18o invenio DAC 40.0′.
Cum BAC 10½ fit DAC 41½.
Cylindro aqua pleno hos angulos quaesivi.

Ga naar voetnoot39)Ga naar voetnoot40)
Si sol altior 58 circiter gradibus non poterunt apparere duo soles oppositi soli vero.
| |
| |
La formule qui permet de calculer l'angle entre le plan vertical passant par le soleil et celui passant par un des parhélies postérieurs peut être établie en partant du calcul correspondant au cas de deux réfractions et d'une réflexion, non pas dans les cylindres verticaux eux-mêmes qui produisent ces parhélies, mais dans une goutte sphérique, en d'autres termes en partant du calcul correspondant au cas de l'arc-en-ciel ordinaire; voir à ce sujet les §§ 27 et 28 du Traité. Nous
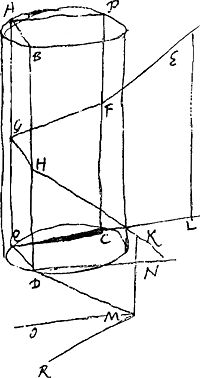
[Fig. 19.]
reproduisons ici la Fig. 19 du § 27, où l'on voit que la projection LCQDM du rayon EFGHK est telle que ∠ LCQ = ∠ QDM et CQ = QD. Cette projection se comporte donc comme un des rayons qui produisent l'arc-en-ciel en passant par des gouttes sphériques. L'angle cherché α, formé par les deux plans verticaux nommés, est égal à celui formé par les deux projections LC et DM.
Au lieu de reproduire exactement le raisonnement de la p. 345 des ‘Opuscula Postuma’, sans doute basé sur les notes de Huygens que nous ne possédons plus (voir le deuxième alinéa de la note 6 de la p. 480), nous pouvons partir du calcul de 1652 sur l'arc-en-ciel (T. XIII, p. 146 et suiv.) que les éditeurs semblent d'ailleurs supposer connu d'après lequel la perpendiculaire abaissée du centre de la circonférence sur le ‘rayon’ LC (on sur le ‘rayon’ DM) est égale à  (note 6 de la p. 149 du T. XIII), c.à.d. à  , où r est le rayon de la circonférence et N l'indice de réfraction ( p/r dans la formule de Huygens). N est ici l'indice de réfraction apparent
| |
| |
correspondant à la projection LCQDM [Fig. 19]; c'est la valeur que l'indice aurait, si LCQDM était réellement un rayon de lumière, en d'autres termes c'est le rapport GC : CK de la Fig. 55, qui, d'après la note 16 de la p. 482, a la valeur  , où n est le véritable indice de réfraction air-eau ou air-glace.
Dans la Fig. 58 (correspondant à la Fig. 15 de la Tab. V des Op. post.), la perpendiculaire nommée sur le rayon incident est  .
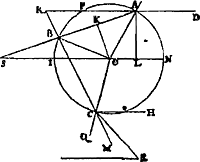
[Fig. 58.]
L'angle γ qu'il s'agit de déterminer est ∠ HCE, double de ∠ BGS, puisque les droites DR, GB et EC se coupent en un point unique. On a donc ∠ HCE = 2 arc BI = 2 (arc AN + arc BI - arc AN) ou ∠ HCE = 2 (2 ∠ BAG - ∠ AGN). D'autre part  ; et  .
On trouve donc finalement

ad inveniendum angulum verticalium circulorum per solem et per parelium alterutrum eorum quae soli sunt ex adversoGa naar voetnoot1).
Ponatur ☉ altitudo eadem quae in quaestione prac. 10 gr.Ga naar voetnoot2).

Ga naar voetnoot3)Ga naar voetnoot4)Ga naar voetnoot5)Ga naar voetnoot6)
| |
| |
| |
| |
| |
§ 5. Arcs inverses.
Dans le § 41 du Traité Huygens indique la méthode pour trouver un nombre quelconque de points des deux arcs inverses touchant la couronne solaire de diamètre de 45o en haut et en bas, en supposant ces arcs produits par des cylindres à noyau horizontaux et en se servant de la table du § 17. La Fig. 59 est à peu près identique, aux lettres près, avec la Fig. 27 du § 41Ga naar voetnoot1).

[Fig. 59.]
HR in parel. Rom. 1630 Ga naar voetnoot2) 
DR. 47.40′
DH. 28.30′
∠ RAN ∞ arc. HC. 48.16′ modò inventumGa naar voetnoot3).
ad examinandum an in parelio Romano 1630, arcus quidam HRC (in fig. parelijGa naar voetnoot4)) hic autem QRB [Fig. 59] inverso situ tangere debuerit coronam PRO [l'une ou l'autre figure]. Quaerendum punctum aliquod in arcu QRB.
| |
| |
| |
| |
| |
| |
| |
| |
Quaeritur aliud punctum in arcu QRB [Fig. 59] .... ∠ MCB [Fig. 56] 6.0′ ... HC. 24.35′ .... BN. 0.36′Ga naar voetnoot21).
Haec puncta inventa sunt hoc modo, ut non opus sit uti linea curva illa quae describitur ope tabellae prius constructae qualis in princ. pag. 9. neque etiam tabella ipsa.
Huygens avait en effet commencé par calculer pour une autre hauteur du soleil (savoir 10o) au-dessus de l'horizon véritable un certain nombre de valeurs correspondantes pour les arcs DL et DB de la Fig. 59, et voulait trouver pour cette hauteur du soleil d'autres valeurs de DB par interpolation: il est fort possible qu'il se soit en effet servi de ce système pour déterminer approxi- | |
| |
mativement un nombre de points des arcs inverses suffisant pour établir leur forme pour différentes hauteurs du soleil. Il dit dans un calcul de la f. 67 v. (portant le no 9): hic arcus DB invenitur ex cognito arcu DL: non autem calculo invenitur sed ope lineae curvae descriptae auxilio tabellae quae initio hujus paginae habetur.
Voici cette table pour la hauteur du soleil de 10o:
| Altitudo ☉ |
∠ CLP [Fig. 56] |
| 0′ |
23.38′ |
| 7.50 |
24.6 |
| 16.6 |
25.28 |
| 24.20 |
28.12 |
| 32.50 |
32.52 |
| 41.48 |
41.34 |
| 51.36 |
60.26 |
| extra ord. 59.0 |
104.30, |
où Huygens annote en marge: Si ad figuram paginae hujus vel pag. 11 [Fig. 59 de la f. 66] hi numeri referantur Altitudo ☉ significat altitudinem ☉ supra basin cylindri hoc est arcum DL. et pro arcu CLP venit arcus LF, vel in minore circulo arcus DB. Circulus magnus ALG intelligitur is esse quem facit planum baseos cylindri aquei continuatum, ipse autem cylindrus axem habet horizontis plano parallelumGa naar voetnoot22).
Figura arcus inversi in parelio HevelianoGa naar voetnoot23) sole alto 20 gr. [Fig. 60], sed tantum pars BCD apparuit, reliquaeGa naar voetnoot24) BA, DE, semper debiliores esse necesse est, idque quo magis a puncto medio C remotae sunt. Pono hic semid. coronae fuisse 23.38Ga naar voetnoot25), licet Hevelius dicat paulo minorem fuisse. nam non multum refert.
Numeri curvis arcubus ascripti sunt gradus altitudinis solis supra bases cylindri, qui ijs in locis arcus videri faciunt. cum autem major est ea altitudo quam 35 vel 40 forsan graduum nimis debilis fit lux ad efficiendos arcus, unde vix unquam puto partes ulteriores arcuum horum, nempe ultra num. 40 cernuntur.
Hic quoque [Fig. 61] ut in superiori ponitur cylindrus glaciatus diametro subdupla ad aqueum. Sol autem in horizonte.
Sole alto 10 gr. [Fig. 62]. Sole alto gr. 30 [Fig. 63]. alt. ☉ 27. [Fig. 64]. alt. ☉ 25o [Fig. 65]Ga naar voetnoot26).
| |
| |

[Fig. 60.]

[Fig. 61.]
[Fig. 62.]

[Fig. 63.]

[Fig. 64.]

[Fig. 65.]
|
-
voetnoot1)
- Nous avons réuni dans cet Appendice tout ce qui se rapporte au calcul des arcs.
-
voetnoot2)
- Manuscrit A, p. 87. Comparez sur cette page l'Appendice VIII qui précède, et le § 4 (note 37 de la p. 486) du présent Appendice.
-
voetnoot3)
- C'est la démonstration du livre G (p. 70 datant de 1691) dont il est question dans la note 1 de la p. 389 qui précède. Les éditeurs des ‘Opuscula Postuma’ ont substitué cette démonstration commençant par ‘In cylindrum ABCD ..’ à celle, plus longue, du § 13, en y apportant quelques changements insignifiants.
-
voetnoot4)
- Les éditions antérieures ont ‘curvae’, apparemment par erreur.
-
voetnoot5)
- Voir pour cette dernière demonstration le § 27 du Traité.
-
voetnoot6)
- Le § 2 contient la formule servant à la composition de la table du § 17 du Traité, ainsi que le calcul numérique, d'après cette formule, de deux angles indiqué's dans cette table. Il s'agit du calcul de l'angle entre le plan vertical passant par le soleil et celui passant par un des parhélies latéraux, lorsque la hauteur du soleil, ainsi que l'indice de réfraction de l'eau (ou de la glace) par rapport à l'air, et le rapport entre le rayon du cylindre d'eau ou de glace et celui de son noyau central de neige, sont donnés. Le cylindre est par hypothèse suspendu verticalement dans l'air.
Sans doute le raisonnement qu'on trouve à la p. 344 des ‘Opuscula Postuma’ a été emprunté à Huygens; voir à ce sujet la note 22 de la p. 482. Nous reproduisons ici [Fig. 55] la figure 14 de la Tab. V des ‘Opuscula Postuma’ en y ajoutant un raisonnement conduisant à la formule qui est en substance le même que celui des p. 343 et suiv. des Op. Post., quoique les notations diffèrent (observons que dans les Op. Post. la même lettre a sert à désigner deux longueurs différentes et que nous avons ajouté à la figure la droite NU).
-
voetnoot7)
- Chartae astronomicae, f. 70. On trouve sur cette feuille et sur la f. 68 les calculs se rapportant aux angles α (hauteurs du soleil) de 5o, 10o, 15o, 20o, 25o, 30o, 35o, 40o, 45o, 50o, 55o, 58o et 60o, pour n = 250/187 et m = 0,473, donc tous les calculs correspondant aux deux premières colonnes de la table du § 17 (pour α = 58o, Huygens trouve β = 78o 24′). Nous ne reproduisons ici que le calcul pour α = 10o, auquel Huygens a ajouté des indications complètes. Les éditeurs des ‘Opuscula Postuma’ ont reproduit le calcul correspondant à α = 25o.
-
voetnoot9)
- 9,2396702 - 10 est donc le logarithme de sin α (sin 10o) et 9,9933515 - 10 celui de cos α, lorsqu'on considère le sinus (ou le cosinus) comme un rapport de deux longueurs, ainsi que nous en avons l'habitude. Mais ce logarithme est le nombre 9,2396702 ou 9,9933515 lui-même, lorsqu'on considère le sinus comme une droite et qu'on donne au rayon du cercle correspondant la valeur 1010, dont le logarithme est 10. Comparez la p. 347 des ‘Opuscula Postuma’ où il est dit: ‘Logarithm. radii = 10.00000’.
-
voetnoot10)
-
n = 250/187 d'après Descartes (voir la p. 11 du T. XIII).
-
voetnoot11)
- Il s'agit d'un angle dont le sinus a la valeur sin α/n.
-
voetnoot16)
-
 . C'est log GC - log DE [Fig. 55], d'après les valeurs de GC et de DE trouvées plus haut. . C'est log GC - log DE [Fig. 55], d'après les valeurs de GC et de DE trouvées plus haut.
-
voetnoot17)
- La page 7 en question enlevée du Manuscrit A, sans doute par de Volder et Fullenius, n'a pas été conservée (voir la note 3 de la p. 360 de l'Avertissement qui précède). Notons que la f. 70 des Ch. astr. (note 7 de la p. 480), d'un format plus grand, ne provient pas du Manuscrit A. Huygens désigne apparemment par ‘termini proportionis refractionis etc.’ les droites GC et DE (ou GC et CK), dont il est question dans la note précédente; comparez la note 3 de la p. 489 qui suit.
-
voetnoot18)
- L'‘angle ADC trouvé à la page précédente’ correspond évidemment à l'angle NCG de la Fig. 55; nous avons appelé m le sinus de cet angle. La ‘pagina praecedens’ est probablement le recto d'un feuillet (portant les no 4 et 13) qui se trouve aujourd'hui dans un des deux portefeuilles contenant les ‘Physica Varia’. Ce feuillet a le même format (note 17) et contient le calcul d'après lequel (l'indice de réfraction air-eau étant 250 : 187) le rapport m du rayon du noyau de la goutte sphérique au rayon de la goutte entière doit avoir la valeur 473 : 1000, pour qu'une couronne d'un diamètre de 44o apparaisse. Le même feuillet contient le calcul de la distance (41o30) d'un parhélie postérieur au soleil lorsque ce dernier a une hauteur nulle (voir la note 1 de la p. 488).
-
voetnoot20)
- On a arc sin m = arc sin (9.6749194 - 10) = 28o14′. Au lieu de prendre la différence (39o33′ - 28o14′), Huygens prend la différence de (90o - 28o14′) et (90o - 39o33′) ce qui revient au même.
-
voetnoot21)
- En doublant la différence 11o19′, on trouve en effet l'angle cherché d'après la formule
 . .
-
voetnoot22)
- Les p. 240-242 du Manuscrit A, auxquels Huygens a donné les nos 4, 5 et 6, contiennent, outre la Fig. 56, des calculs tels que celui reproduit dans le texte. Il s'agit d'un calcul antérieur à celui du § 1, vu que ce dernier correspond à la page qui portait le no 7 (note 17 de la p. 482). La Fig. 56 ressemble beaucoup à la Fig. 55 tirée des ‘Opuscula Postuma’. La page 7 (ou la p. 8) contenait sans doute une figure du même genre, qui a servi de modèle aux éditeurs. On voit que le calcul des p. 4, 5 et 6 est plus primitif, puisque Huygens ne commence pas par donner une valeur déterminée à la hauteur α du soleil, mais qu'il en donne une à l'angle MCB (correspondant à l'angle CGF de la Fig. 55). Il prend successivement ∠ MCB = 6o, 12o, 18o, 24o, 30o, 36o, 38o et 41o40′.
-
voetnoot23)
- On a en effet, puisque le triangle sphérique correspondant au trièdre CBDM est rectangle, cos BCD = cos MCD. cos MCB, d'où BCD = 32o6′.
-
voetnoot26)
- On a en effet OB : BD (= EB : BM) = 4 : 3 (indice de réfraction); donc, en prenant BA = CB, sin BAO : sin BCD = 4 : 3.
-
voetnoot30)
- C'est l'angle cherché (double de l'angle CML), savoir l'angle des plans verticaux passant respectivement par le soleil et par un parhélie. Il va de soi qu'il n'y a pas de table dans le Traité correspondant à ce calcul où n = 4/3 et m = ½, ce qui sont des valeurs approchées.
-
voetnoot31)
- Chartae astronomicae, f. 68. 1000 : 680 est le rapport du rayon du noyau au rayon extérieur (voir la fin du § 5 du Traité) dans le cas des gouttes sphériques produisant une couronne d'un diamètre de 90o. On trouve sur la même feuille le calcul dans le cas des gouttes qui conduit à cette valeur du rapport.
-
voetnoot32)
- Nous ne reproduisons que le calcul pour α = 10o. Huygens exécute le calcul en outre pour α = 5o, 15o, 20o, 25o, 30o, 33o, 34o et 35o. Nous possédons donc tous les calculs correspondant aux deux dernières colonnes de la table du § 17 (le calcul pour α = 33o et 34o est incomplet; pour α = 40o Huygens arrive à la conclusion: non potest).
-
voetnoot33)
- Voir pour le nombre 0,12905 le texte et les notes 16 et 17 de la p. 482.
-
voetnoot35)
- C.à.d. β = 46o 44′. Comparez le calcul de la p. 480.
-
voetnoot36)
- Le § 4 contient, outre quelques déterminations expérimentales, la formule servant à la composition de la table du § 28 du Traité, ainsi que le calcul numérique, d'après cette formule, d'un des angles indiqués dans cette table. Il s'agit de l'angle γ - DAC ou DAF dans la Fig. 57 - entre le plan vertical passant par le soleil et celui passant par un des parhélies postérieurs, lorsque ... dans l'air. (voir la note 6 de la p. 480).
-
voetnoot37)
- Manuscrit A, p. 87 et 88 (février ou mars 1659). Huygens détermine par expérience l'angle 2 γ des plans verticaux dans lesquels sont situés les parhélies postérieurs, à l'aide de son cylindre de verre, à noyau de bois, rempli d'eau, dont il est aussi question dans le § 4 de l'Appendice VII au mois d'avril de la même année. Voir aussi sur les expériences faites avec ce cylindre le § 11 du Traité, ainsi que le deuxième alinéa de la p. 506 qui suit. En comparant le résultat des expériences avec la table du § 28 on constate de notables divergences, comme on pouvait s'y attendre.
-
voetnoot36)
- Le § 4 contient, outre quelques déterminations expérimentales, la formule servant à la composition de la table du § 28 du Traité, ainsi que le calcul numérique, d'après cette formule, d'un des angles indiqués dans cette table. Il s'agit de l'angle γ - DAC ou DAF dans la Fig. 57 - entre le plan vertical passant par le soleil et celui passant par un des parhélies postérieurs, lorsque ... dans l'air. (voir la note 6 de la p. 480).
-
voetnoot38)
- Ce dernier angle a évidemment été calculé. C'est la distance BE qui sépare les points B et E (parhélies) de la Fig. 57, mesurée selon l'arc d'un grand cercle (ce n'est donc pas l'angle 2 γ). Comme ZB = ZE = 68o et ∠ BZE = 75o on a sin ½ BE = sin 37o 30′. sin 68o, d'où BE = 68o 44′ à sort peu près.
-
voetnoot39)
- L'angle BAC est la hauteur du soleil, que nous appelons α, comme dans le § précédent.
-
voetnoot1)
- Chartae astronomicae, f. 70. On trouve sur cette feuille et sur la f. 68 les calculs se rapportant aux angles α (hauteurs du soleil) de 5o, 10o, 15o, 20o, 25o, 30o, 35o, 40o, 45o, 50o et 58o pour n = 520/187 et m = 0,473 (comparez la note 7 de la p. 480), donc tous les calculs correspondant à la table du § 28 excepté celui pour α = 0o sur lequel on peut consulter la note 18 de la p. 482. Nous ne reproduisons ici que le calcul pour α = 10o, auquel Huygens a ajouté des indications complètes. Les éditeurs des ‘Opuscula Postuma’ ont reproduit le calcul correspondant à α = 25o.
-
voetnoot2)
- Comparez la p. 480; la ‘quaestio praecedens’ est la question des parhélies latěraux.
-
voetnoot3)
- C'est le logarithme de l'indice de réfraction apparent N; voir les notes 16 et 17 de la p. 482.
-
voetnoot5)
- En marge: brevitatis gratia possit addi log. radij minus log. 2. nempe 9.6989700.
-
voetnoot8)
- En marge: posset brevitatis gratia addi log. 2 - log. √3 nempe 0,0624694.
-
voetnoot1)
- Comme le texte le fait voir la Fig. 59 se rapporte au cas d'une couronne solaire d'un diamètre supérieur au diamètre ordinaire. Au § 41 Huygens dit d'ailleurs qu'on peut de la même manière construire par points les arcs inverses touchant des couronnes plus grandes.
-
voetnoot2)
- Chartae astronomicae f. 66. Voir sur les six parhélies observés à Rome en 1630 le no V de l'Appendice V qui précède, en particulier la note 2 de la p. 466. Les grandeurs des arcs HR etc. sont empruntées à la lettre de Scheiner (Appendice VI). La couronne solaire de la Fig. 59 à rayon DR = 47o40′ est la plus grande des deux couronnes concentriques observées.
-
voetnoot3)
- La f. 66 des Ch. astr. porte le no 11; c'est un des feuillets enlevés du Manuscrit A, dont il est question dans la note 17 de la p. 482. La f. 66 fait done suite à la f. 67 de même format des Ch. astr., qui porte le no 10. On trouve en effet sur la f. 67 le calcul de l'arc HC, avec la remarque: vide fig. pag. praec. [cette page fait défaut] vel pag. sequ. [c'est la Fig. 59 du texte]. Nous intercalons donc ici le calcul de l'arc HC d'après la f. 67; cet arc HC correspond à une orientation donnée du cylindre à noyau horizontal, savoir une orientation telle que le rayon du soleil tombant sur lui et réfracté de telle manière qu'il frise le noyau fait, en parcourant le cylindre, un angle de 12o (valeur arbitrairement choisie) avec la base ou section droite du cylindre.
-
voetnoot4)
- Il s'agit de la figure correspondant au texte de la lettre de Scheiner de l'Appendice VI.
-
voetnoot5)
- C'est bien à la Fig. 56 que le texte qui suit s'applique, puisque la f. 67 des Ch. astr. porte l'indication: vide fig. pag. 5 retro; or cette ‘pag. 5’ est la p. 241 du Manuscrit A (voir la note 17 de la p. 482).
-
voetnoot6)
- Le calcul qui sert à déterminer l'angle que le rayon AB du soleil incident sur le cylindre fait avec la base ou section droite, serait identique avec celui de la p. 483, si l'angle MCD avait la même valeur. Mais cet angle qui était de 30o à la p. 483 est maintenant de 44o, puisque la valeur m attribuée au rapport du rayon du noyau au rayon du cylindre entier n'est apparemment plus 1 : 2, mais 695 : 1000 - on a sin 44o = 0,695 -; ce rapport s'accorde avec le rayon de la couronne (note 2 de la p. 490), puisqu'un calcul analogue à celui du § 5 du Traité fait voir que pour m = 0,69465 (arc sin 44o) et n (indice de réfraction) = 4/3, on trouve une couronne d'un rayon de 47o42′. Ce calcul ou plutôt cette vérification, puisque Huygens part de la valeur ∠ MCD = 44o, commençant par les mots: 47.40 semid. coronae majoris Scheineri, in qua parelius verticalis. ergo crassitudo cylindri glacialis major quam subdupla aquei. quare primum quanta sit et conduisant à la valeur 47o42′, se trouve en effet sur la f. 67. La couronne est ici produite par hypothèse non pas par des gouttes sphériques, mais par les extrémités arrondies des cylindres (voir la fin du § 41 du Traité) qui causent une réfraction à peu près identique avec celle due aux gouttes sphériques. Le rapport m est par hypothèse le même pour les extrémités arrondies que pour le reste du cylindre. C'est par hasard que la calcul de la p. 483-484 conduit également à une valeur de 16o6′ pour l'angle
BAE.
-
voetnoot9)
- Comme à la p. 483, l'indice de réfraction air-eau ou air-glace est ici par hypothèse 4/3 et non pas 250/187, ce qui fait voir qu'il s'agit d'un calcul non destiné à être publié.
-
voetnoot10)
- L'inclinaison BAE [Fig. 56] du rayon incident sur le cylindre par rapport à sa base correspond en effet à l'arc DL de la Fig. 59, lequel représente la hauteur du soleil par rapport à l'horizon fictif [voir le § 41 du Traité] AFLG parallèle au plan de base du cylindre à noyau horizontal, qu'on voit au point B.
-
voetnoot11)
- C'est l'angle des plans verticaux par rapport à l'horizon fictif, passant respectivement par le soleil et par un des parhélies latéraux (le cylindre considéré étant vertical par rapport à l'horizon fictif).
-
voetnoot12)
- D'après le § 41 du Traité les points cherchés des arcs inverses se trouvent sur des circonférences de cercle passant par le soleil et parallèles à des horizons fictifs tels que AFLG [Fig. 59], la distance du point cherché au soleil étant égale à l'angle entre deux plans perpendiculaires à cet horizon fictif et passant respectivement par le soleil et par un des parhélies qui se formeraient si les axes de tous les cylindres horizontaux par rapport à l'horizon véritable étaient perpendiculaires à l'horizon fictif, c.à.d. parallèles à celui du cylindre considéré dans la Fig. 59. L'arc BD (ou l'arc LF) a donc le même nombre de degrés que l'angle CLP de la Fig. 56.
-
voetnoot13)
- On a en effet sin LAD = sin DL : sin AD, puisque l'angle L est droit.
-
voetnoot15)
- Il s'agit du logarithme de la tangente de l'arc BF.
-
voetnoot16)
- On a en effet tg FAB = tg BF : sin AF, puisque l'angle F est droit.
-
voetnoot17)
- Ici finit le calcul emprunté à la f. 67 des Chartae astronomicae: voir la note 3 de la p. 490. Le calcul qui suit est donc emprunté à la f. 66.
-
voetnoot18)
- Dans la Fig. 59 RN fait partie d'un grand cercle qui touche la couronne solaire en R. On a évidemment ∠ RAN = HC.
-
voetnoot19)
- On a en effet tg AN = tg. AR : cos RAN, puisque l'angle R est droit.
-
voetnoot20)
- Le calcul conduit donc finalement à la détermination exacte des coordonnées d'un point B de l'arc inverse par rapport à la couronne solaire. Ces coordonnées sont RN = 48o16′ et NB = 2o43′.
Remarquons en passant que le grand cercle ANC ne touche pas la couronne solaire comme la figure pourrait le faire croire: l'arc HC, exprimé en degrés, est plus grand (quoique bien peu) que le rayon de la couronne.
-
voetnoot21)
- Nous supprimons le calcul (f. 66) qui est analogue au calcul précédent. Les coordonnées du deuxième point de l'arc inverse par rapport à la couronne solaire sont donc RN = 24o35′ et NB = 0o36′.
-
voetnoot23)
- Chartae astronomicae, f. 69. Comparez le § 35 du Traité. Dans le phénomène de Hevelius (ou de Danzig) il y avait deux couronnes solaires concentriques, dont chacune était touchée en haut par un arc inverse, comme la Fig. 22 l'indique. Huygens dit plus loin que le rapport m du rayon du noyau du cylindre à celui du cylindre lui-même était environ 1 : 2; en effet il parle ici de l'arc inverse qui touchait la couronne intérieure dont le diamètre était de 45o; comparez sur la production de la couronne par la réfraction des rayons solaires dans les extrémités arrondies des cylindres horizontaux la fin de la note 6 de la p. 492.
-
voetnoot25)
- C'est la valeur du rayon correspondant à m = 1 : 2 (note 23) et n (indice de réfraction) = 4/3.
-
voetnoot26)
- Pour trouver les points des arcs inverses des Fig. 60-65 Huygens doit avoir exécuté un grand nombre de calculs du même genre que ceux qui précèdent, mais ces calculs n'ont pas été conservés. Voir sur les arcs inverses la p. 360 de l'Avertissement qui précède.
|


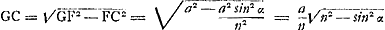 . Les triangles NUG et CQG étant semblables, on a
. Les triangles NUG et CQG étant semblables, on a  . On tire ensuite des triangles semblables FCQ et FDI :
. On tire ensuite des triangles semblables FCQ et FDI :  . Or DE = a cos α. Donc sin
. Or DE = a cos α. Donc sin 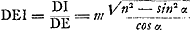 . L'angle DEI est égal à l'angle TCN. L'angle β qu'il s'agit de trouver est le double de la différence de l'angle TCN et de l'angle GCN (c.à.d. le double de l'angle GCT), donc
. L'angle DEI est égal à l'angle TCN. L'angle β qu'il s'agit de trouver est le double de la différence de l'angle TCN et de l'angle GCN (c.à.d. le double de l'angle GCT), donc

 , nous apprend que pour m = 0,68, N a tout au plus la valeur 1/0,68. On en tire (pour n = 250/187) α = 34o40′ à peu près, et ensuite β = 94o20′.
, nous apprend que pour m = 0,68, N a tout au plus la valeur 1/0,68. On en tire (pour n = 250/187) α = 34o40′ à peu près, et ensuite β = 94o20′.
 .
.

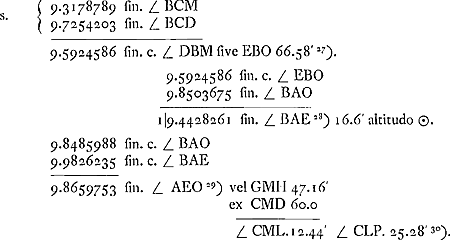




 (note 6 de la p. 149 du T. XIII), c.à.d. à
(note 6 de la p. 149 du T. XIII), c.à.d. à  , où r est le rayon de la circonférence et N l'indice de réfraction (p/r dans la formule de Huygens). N est ici l'indice de réfraction apparent
, où r est le rayon de la circonférence et N l'indice de réfraction (p/r dans la formule de Huygens). N est ici l'indice de réfraction apparent
 , où n est le véritable indice de réfraction air-eau ou air-glace.
Dans la Fig. 58 (correspondant à la Fig. 15 de la Tab. V des Op. post.), la perpendiculaire nommée sur le rayon incident est
, où n est le véritable indice de réfraction air-eau ou air-glace.
Dans la Fig. 58 (correspondant à la Fig. 15 de la Tab. V des Op. post.), la perpendiculaire nommée sur le rayon incident est  .
.

 ; et
; et  .
.